基于隐马尔科夫模型的电动汽车充电优化
刘梦悦,周 力,李 炜,芮世昊
(1.安徽工程大学 电气工程学院,安徽 芜湖 241000; 2.大陆汽车电子(芜湖)有限公司,安徽 芜湖 241000)
基于隐马尔科夫模型的电动汽车充电优化
刘梦悦1,周 力1,李 炜1,芮世昊2
(1.安徽工程大学 电气工程学院,安徽 芜湖 241000; 2.大陆汽车电子(芜湖)有限公司,安徽 芜湖 241000)
针对电动汽车应用隐马尔科夫模型对单个车辆在一天的任何时候被使用的概率建模,捕捉不同的行程时间段,构建出行状态转移概率矩阵刻画驾驶模式与日分时电价行为的各个变量之间在时间维度上的关联性。根据车辆的使用情况、终端用户的风险规避和电力价格,对样本在仅充电方案和V2G方案下使用随机动态规划来确定最优充电策略。
电动汽车;隐马尔科夫;驾驶模式;分时电价
人类行为的复杂性指出了电动汽车使用的随机性。电动车电池的主要目的是提供电力驱动车辆。因此,电池需存储足够能量来保证行程的完成,这个叫决策工具,它与汽车使用的随机模型相结合[1-2]。
文献[3]对智能电网中电动汽车的有序充电调度进行了综述,提出了用电价杠杆调节电动汽车快充负荷的实时电价机制,达到电网、充电站和用户的共赢。文献[4]提出了一种电力市场环境下的电动汽车调度方法,通过选择电价较低时段充电和向系统提供调频或旋转备用,以使电动汽车的总充电成本最小化。文献[5-6]对模糊神经网络进行训练,生成了驾驶意图模糊推理规则。
1 隐马尔科夫模型
隐马尔科夫模型(Hidden Markov Models,简称HMM)不但可对不可观测状态的信息状态及其转移过程建模,还能够对不可测状态与可测关联变量的函数关系建模。由于HMM模型由马尔科夫链和一般随机过程共同组成,因此描述状态转移和时间序列方面具有双重优势。
1.1 隐马尔科夫模型定义

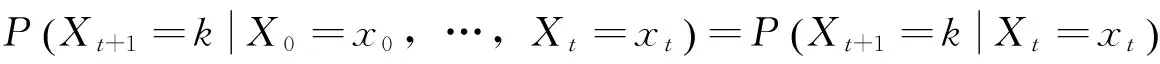
(1)

(2)
表示在t时刻从状态j转移到t+1时刻的状态k。如果转移概率不依赖于t,这个过程被称为齐次马尔可夫链。如果转移概率取决于t,这个过程被称为一个非齐次马尔可夫链。以分钟作为采样时间,考虑到一天有1 440 min,那么就假设rjk(t)=rjk(t+1 440),转换概率矩阵用M(s)表示,矩阵描述的在状态N的特定车辆的驾驶模式
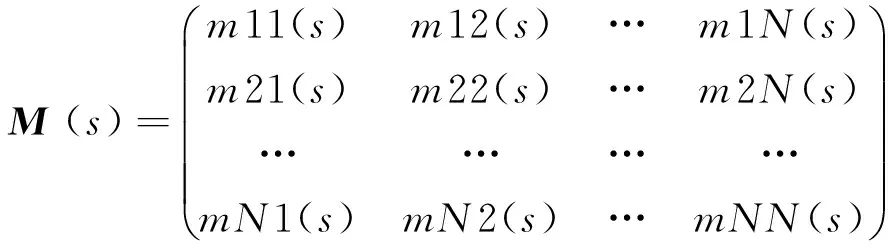
(3)


(4)
1.2 隐马尔科夫模型
标准的马尔科夫模型可以只包括状态,因此如果数据只提供车辆驾驶或不驾驶状态,那么从当前状态转移到另一个状态所耗时间不取决于已经花费在当前状态的时间量。就车辆而言,这意味着行程结束的概率并不取决于行程的时间持续多久。这对建立捕捉车辆实际驾驶的模型似乎是不现实的。
克服此因素,我们使用一个隐马尔科夫模型,它可估计那些数据里不能直接观察到额外的状态。事实上,可以估计在每个状态的等待时间去匹配实际观察到的数据。通过在马尔可夫链的基础上引进一个新的状态添加为一个隐藏的状态。事实上,一旦车辆实际执行起来就可以提供更多的驾驶数。
(5)
给出标准马尔可夫链的状态依赖分布,表示状态值与观测值之间的概率分布。矩阵U(zt)由uzk(t)组成:
LT=ΛU(z1)P(2)U(z2),…,P(T)U(zT)
(6)
其中:Λ是X1初始分布。

2 行程分布拟合
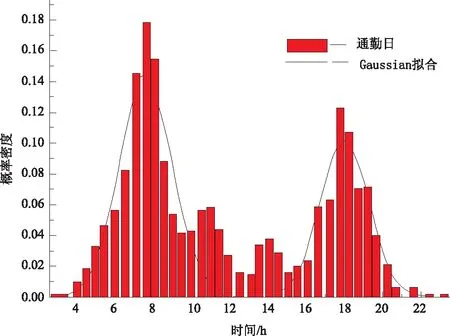
图1 某地居民通勤日出行量
通过调查平台,据2009年美国交通部调查(NationalHouseholdTravelSurvey,NHTS)对全美居民出行情况进行调研,选取某通勤日小区居民日出行量情况分析。对数据进行批处理,从数据总库中提取出行OD(Origin-Destination)信息[7]。
应当考虑辨识车辆是否在驾驶,但不能辨别出正处于哪种驾驶状态。此外,隐藏的驾驶状态是不直接从数据判断的。在实践中,它们可能对应于不同的环境中驾驶(城市/农村)或不同的速度。计算隐状态之间的转移概率通过行程持续时间概率分布结果反应在数据上。此外,为适应模型数据,我们假设只有每天不开车状态的转移概率,减少了估计过程的复杂性。
2.1 拟合时变参数
估计从车辆停止状态到驾驶状态的转移概率,因为停状态和转换来自数据中直接观察到的,可以使用这个过程描述转移估计。这个数据分为两个部分:通勤日和非通勤日。需采用Gaussian进行拟合,决定系数R2=0.776 7,拟合结果如图1所示。
研究昼夜变化发现,工作日出行OD时刻出现了明显双峰现象,约18%出行在早上07:00~08:00,约12%大致分布在17:00~19:00。同时,没有观察到00:00~5:00有出行。因此,在现行交通组织形式下,车辆在通勤日仍出现了早晚高峰,错峰上下班的效果并未充分显现。其他模式被发现在周末,但是这些不涉及任何方法论的差异,我们限制自己在工作日开始旅行。年度变化也可能存在,但是有限的数据样本不允许捕捉这样的季节性。
2.2 拟合时不变参数
估计时不变参数,在一段行程里适当的概率分布被拟合。在式(6)中通过概率估计给出定常参数估计。对于一个给定数量的驾驶状态,一旦N状态被拟合,可以测试如果添加一个额外的状态拟合可以得到显著的改善。N状态模型是N+1状态或更多状态的分模型。根据概率比增加状态数目,直到没有观察到测试有显著改善再停止。
假设开始充电时刻为最后一次出行返回时刻,电动汽车在家充电开始时刻近似满足如下伽马分布。
(7)

3 一个随机动态规划问题
终端用户期望车辆可以充电并由他们自由选择、判断,同时尽量减少车辆的运行成本。电力需求的变化和来自可再生能源的电力生成可延迟终端用户车辆的充电,这就意味着用户面临充电推迟使成本最小化或者用户立刻充电使车辆可用性最大化。
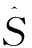

(8)
使用倒推法找出最优离散化策略∏*,发现最优离散化策略∏*依靠于时间t和电池状态s。由于电网分时电价的划分可能出现电价为平段却存在负荷小高峰的情况,若采用电网分时电价来引导电动汽车充电,可能导致负荷峰值增大的后果[10],而且也不利于充电经济性。
4 结果与讨论
4.1 仅充电的方案

表1 家用电动汽车参数
以特斯拉MODEL S为例,对家用汽车的具体参数作出一些假设,如表1所示。
关于电力价格,本文采用的是电动汽车分时电价数据[8]。图2显示了行程开始电力价格时变(real-time pricing,RTP)图和最优策略值的估计时变曲线图。即最优政策表明电动汽车是否应该在t时刻充电。对于充电或不充电,最优策略的取值在{1,0}。图2表明,纵轴上充电的不同等级显示了电池的状态,表示出了电池容量的百分比。水平轴表示时间。图2只显示当车辆不开车时充电决策,我们假定它是不可能停止行程和再充电,除非电池完全耗尽。从这个图可以观察到,如果电池的能量水平是5%,最优决策总是在控制的,除了那些当驾驶的概率很低和电力价格是特别高的时期。相反,如果电池的能量水平是65%,那么车辆只有当能源价格相对较低时充电。当电荷接近100%的时候,充电策略显得更加极端化。事实上,如果电池的能量等于电池存储能量的95%,那么电动汽车只有在能源价格被认为是那段期间最低值时才会充电[9]。
4.2 V2G方案
允许车辆向电网供电的电池有可能有助于降低峰值功率需求的影响,这个操作模式通常被称为V2G计划[10]。V2G方案研究是从单个车辆的角度。
V2G实施方案是通过设置最小充电功率umin=-4 kW并保持所有其他参数值不变。绘制电价时变曲线及电池充电在不同情况下的时变概率如图2、图3所示。获得的最优策略,实现φ=12¥/h的V2G方案如图3所示。这类似于图2,除了最优政策取值为{1, 0,-1} ,分别对应充电、不充电、放电。观察电池电量水平在较低的时候,最优策略几乎一直作用于每个充电时间t,除了电价处于峰值时刻和低概率驾驶期间。随着电池电量的增加,这个策略在电价处于峰值改变供电到电网里去和在电价低谷时充电。提出的V2G算法来权衡花费与电池耗尽之间的关系,对当电价低的时候延迟充电和电价高得时候向电网供电来获取利益。在图3中,显示最优政策显示了一些“峰值”,在短时间内从充电到不充电最优决策被改变。电价的交易与每小时的时间分辨率有关,因此价格变化只有每小时和相应的价格变化可能很大。作为每一分钟的车辆决定适当的操作,它能够利用这个充电策略。

图2 电池充电的不同等级的时变概率 图3 电池充电的不同等级罚金制约V2G的时变概率
5 结 语
本文提出了一种说明用户的驾驶模式不确定性算法的电动汽车充电优化。该算法是建立了一个隐马尔可夫链模型,提供了车辆在一天的任何时候被使用的概率和捕捉不同的行程时间段。根据车辆的使用情况、终端用户的风险规避和电力价格,使用随机动态规划来确定最优充电策略,适应任何特定的车辆使用户节省运营成本,甚至在V2G计划下获得利润。
[1] Song Yonghua,Yang Xia,Lu Zongxiang.Integration of plug-in hybrid and electric vehicles : experience from China[C]//Proceedings of 2010 IEEE Power Engineering Society General Meeting.Minneapolis,MN,USA:2010:1-5.
[2] 顿顶,宋永华,胡泽春,等.电动汽车参与V2G的最优峰谷电价研究[J].中国电化工程学报,2013,31:15-25+2.
[3] 唐小波,赵彩虹,吴薛红,等.智能电网中电动汽车快速有序充电实时电价优化方法[J].南京师范大学学报(工程技术版),2013,13(4):13-18.
[4] Caramanis M,Foster J M.Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion[C]//Proceedings of the 48th IEEE Conference on Decision and Control,2009:4717-4722.
[5] 钱立军,袭著永,赵韩基.于模糊神经网络的混合动力汽车控制策略[J].仿真系统仿真学报,18(5):1384-1387.
[6] 王庆年,唐先智,王鹏宇,等.基于神经网络的混合动力汽车驾驶意图识别方法[J].农业机械学报,2012,48(3):32-36
[7] 曾丹,姚建国,杨胜春,等.应对风电消纳中基于安全约束的价格型需求响应优化调度建模[J].中国电机工程学报,2014,34(31):5571-5578.
[8] 阮文骏,王蓓蓓,李扬,等.峰谷分时电价下的用户响应行为研究[J].电网技术,2012,36(7):86-93.
[9] 胡迪鹤.随机环境中的马尔可夫过程[M].北京:高等教育出版社,2011:7.
[10] 孙晓明,王玮,苏粟,等.基于分时电价的电动汽车有序充电控制策略设计[J].电力系统自动化,2013,37(1):191-195.
Electric Vehicles Charging Optimization Based on Hidden Markov Model
LIU Mengyue1, ZHOU Li1, LI Wei1, RUI Shihao2
(1.Anhui Polytechnic University, Wuhu 241000, China;2.Continental Automotive Wuhu Electronics Co Ltd, Wuhu 241000, China)
An optimal charging method for electric vehicles is presented by modeling the probability of the use of a single vehicle at any time though a day based on hidden Markov model,the parameters of different travel time are captured, than the travel state probability matrix, which depicts the relevance of each variable of driving mode and daily time-sharing electricity price behavior on the time dimension is built. According to the factors of usage of the vehicle, risk aversion for terminal users and electricity prices, the stochastic dynamic for the sample under the conditions of only charging and V2G is programmed. Finally, the optimal charging strategy for electric vehicle is determined.
electric vehicles; Hidden Markov; driving mode; time-sharing electricity
2016-11-19
刘梦悦(1991-),女,江苏泗阳人,在读硕士研究生,主要从事自动控制、计算机控制方面的研究.
安徽省高校自然科学研究重点项目(KZ00216024).
10.3969/i.issn.1674-5403.2017.01.018
TP273
A
1674-5403(2017)01-0066-04

