基于DEA模型的高铁站换乘效率研究
原 静,吴智伟
(长安大学 公路学院,陕西 西安 710064)
基于DEA模型的高铁站换乘效率研究
原 静,吴智伟
(长安大学 公路学院,陕西 西安 710064)
为了提高高铁站的综合换乘效率,以平均换乘时间、平均换乘距离两个指标为输入指标;乘客换乘满意度、换乘方式吸引度两个指标为输出指标,运用DEA(数据包络分析)理论建立相应的DEA非均一评价模型。分别对西安北站内地铁、出租车、公交车3种换乘方式进行换乘效率评价与研究。
高铁站;DEA模型;换乘效率;换乘方式
随着高铁的快速发展和新型高铁站的出现,研究高铁站内不同换乘方式的换乘效率显得十分重要。1978年,E.Rhodes给出了评价决策单元相对有效性的数据包络分析方法[1](Data Envelopment Analysis,简称DEA)。该方法是目前评价具有多目标输入和多指标输出系统较为有效的方法。2003年,卢艳秋、金俊武首次将DEA应用于铁路运输价格评价中,他们在经典DEA模型的基础上增加了多个评价准则,从而对运输价格的合理性进行有效评价[2]。2004年,Yoshida应用DEA模型于日本机场效率的比较,验证了1950年后日本机场的建设遭受过度投资[3]。以上的研究都是应用DEA单一评价方法。本文将传统的DEA模型与层次分析法相结合建立DEA非均一评价模型[4],并将关注点置于特定方式的换乘效率,提出更能表征换乘效率的换乘吸引率作为输出指标。
1 非均一的DEA评价模型
假设现有n个决策单元Uk(k=1,2,...n),每个决策单元都有m种类型的投入(m种资源的消耗)以及s种类型的产出(s种产品),分别用向量Xk=(x1k,x2k,...,xik,...,xmk)T和Yk=(y1k,y2k,...,yrk,...,ysk)T表示。其中,xik表示第k个决策单元对第i种资源的消耗量;yrk表示第k个决策单元对第r种类型产品的输出量。
(1)
式中:ur、vi分别为相应指标的权重系数;Ek为Uk的效率值[5]适当选取u、v可使Ek<1.0,并且Ek越大说明第k种换乘方式换乘效率越高。因此第k0种换乘方式换乘效率评价指数可以由数学规划模型的最优值确定。
(2)
(3)
式中:权重向量u、v是规划模型的决策变量,其最优解有利于第k0种换乘方式换乘效率指标的权重分配。通过引入Chames-Cooper变换以及线性规划的对偶原理有:
min[θ-ε(eTs-+eTs+)]
(4)
(5)
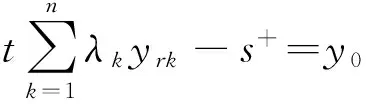
(6)
式中:θ为第k0种换乘方式换乘效率的评价指标;λk为相对于第k0种换乘方式构造一种有效换乘方式组合中第j种换乘方式的组合比例;s-、s+为松弛变量。
2 评价分析方法

3 评价指标体系的建立
3.1 评价指标的选取
通过对换乘系统的分析研究,将选取的换乘评价指标为:输入指标包括平均换乘时间和平均换乘距离。输出指标包括乘客换乘满意度和换乘吸引度。
3.1.1 平均换乘时间
平均换乘时间是指旅客在高铁站完成换乘所需的平均时间,本研究中采用对乘客进行抽样调查得到不同换乘方式的平均换乘时间,即:
(7)
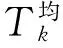
3.1.2 平均换乘距离
各换乘方式的换乘距离可由实测获得,可以分别得到3种换乘方式的换乘距离分别为l地铁、l公交车、l出租车。
3.2 乘客换乘满意度
3.2.1 换乘满意度的指标选取
换乘满意度是乘客的主观感受,乘客会对换乘方式服务的各个方面做出主观评价,这里选择舒适度、方便与快捷、乘车环境3个方面进行分析,用层次分析法分析这3个方面对乘客选择换乘方式的影响程度。
3.2.2 层次分析法
层次分析法通过分析复杂问题所包含的因素及其相互关系,将问题分为不同的要素,并将这些要素归为不同的层次,从而形成多层次结构。① 构造判断矩阵:根据层次结构模型每层中各因素的相对重要性,给出判断数值列表,形成判断矩阵。② 计算层次单排序:层次单排序是根据判断矩阵,计算对上一层某元素而言,本层次与之有联系的元素的重要性次序的权值。③ 计算各层元素组合权重:利用同一层次中所有层次单排序的结构,可以计算具体指标层各元素关于目标层的权重。④ 一致性检验:计算各层次元素对于目标层的总排序权重并对层次进行组合一致性检验。
3.2.3 各指标权重的确定
根据调查资料并通过层次分析法进行计算,对其进行一致性检验的结果,RI=0.078<0.1,判断矩阵的一致性达到了要求,可得各指标的权重如表1所示。

表1 指标权重
3.2.4 换乘满意度的计算
换乘满意度的调查采用5分制的Liker量表,1分~2分表示高度满意,3分表示一般,4分~5分表示低度满意。具体计算如下:
(8)
式中:αm为m指标的权重;gmpi为i出行方式对m指标的打分;q为调查总人数;Li为i出行方式出行满意度总评分。
3.2.5 换乘吸引度
设i种换乘方式的吸引度为ki,i种换乘方式实际小时客运量为vi,i种换乘方式的小时运营能力Vi,则有:
ki=vi/Vi
(9)
4 实例分析
以西安北站为例,分析地铁、公交车和出租车的换乘效率。本次调查采用在公交车站、地铁进出口和出租车停靠点随机抽样,现场收发问卷的方式。共采集调查样表263份,经筛选后合格231份。经统计可得评价指标初始值如表2所示。

表2 评价指标初始值
将表2中得到的数据分别代入DEA模型中,应用DEAP2.1软件并对结果进行整理,得到西安北站各换乘方式运行效率评价结果如表3所示。

表3 西安北站各换乘方式运行效率评价结果
从表3可以看出,只有公交车一种换乘方式的综合技术效率、纯技术效率、规模效率达到了DEA有效,而地铁和与出租车两种换乘方式只有纯技术效率达到了DEA有效,综合技术效率与规模效率未达到DEA有效。地铁与出租车综合技术效率较低的原因是因为其规模效率没有达到最优。综合效率、纯技术效率、规模效率的分析如下:
(1)综合效率分析。
DEA方法下的技术效率是换乘方式的综合效率指标,是纯技术效率与规模效率的乘积。从表3可以看出,从综合技术效率来看,公交车的综合技术效率达到了有效,地铁以及出租车的综合技术效率较低,存在较多的资源浪费,说明这两种换乘方式的投入产出结构不合理。
(2)纯技术效率分析。
从纯技术效率层面看,3种换乘方式的纯技术效率都达到最优,说明各换乘方式的资源组合达到最优。
(3)规模效率分析。
规模效率表示系统在最大产出下,技术效率的生产边界的投入量与最优规模下投入量的比值,可以衡量在投入导向下,各换乘方式的换乘效率是否处于最优生产规模。从规模层面看,地铁和出租车的规模效率没有达到最优,说明投入规模过大,从另一方面来讲,说明地铁和出租车的换乘潜力并没有完全挖掘出来,可以通过改进管理措施进一步提高其换乘效率。
5 结 语
本文利用DEA非均一评价模型建立了高铁站不同方式换乘效率的评价模型,以平均换乘时间,平均换乘距离为输入指标,应用DEAP2.1软件输出乘客换乘满意度、换乘方式吸引度两个指标进行评价。并且对西安北站不同换乘方式的换乘效率做了实例分析。从评价结果来看,本文得到的结论与现实情况基本吻合。利用DEA非均一评价方法不仅可以定性的评价出各换乘方式的优劣,还能够给出不同换乘方式优劣的差距来源。DEA非均一评价模型评价结果能够指导今后的交通管理与投资。
[1] 郭谦,吴殿廷,鲍捷.基于换乘效率指数的北京轨道交通网络通达性评价及其成因分析[J].经济地理,2012.32(11):39-44.
[2] 郭琴,王元庆.公共自行车与轨道交通换乘效率评价指标体系[J].交通运输工程与信息学报,2014,12(1):11-16
[3] 郝晋峰,杨扩. 轨道交通枢纽换乘效率评价指标构建[J]. 军事交通学院学报,2015,4(6):56-60.
[4] 叶臻,关宏志.城市轨道交通枢纽换乘供需的分形综合评价[J].长安大学学报(自然科学版)2014,34(1):95-102.
[5] 朱昌峰.基于DEA的城市轨道交通运营安全评价与分析[J].兰州交通大学学报,2010,29(3):67-70.
[6] 蒋文.基于区间 DEA 模型的轨道交通衔接模式选择评价研究[J].交通运输系统工程与信息,2012,12(6):132-136.
[7] 周强,秦菲菲,吴戈.基于DEA方法的城市轨道交通系统效率评价研究[J].铁道运输与经济,2014,36(2):79-83.
Research on Transfer Efficiency of High-Speed Rail Station Based on DEA Model
YUAN Jing, WU Zhiwei
(Chang′ an University,Xi′an 710064, China)
In order to improve the comprehensive transfer efficiency of high-speed rail station, the average transfer time and the average distance of transfer are thought of as input indicators, and satisfaction of passenger transfer and transfer attract are taken as output indicators. Corresponding DEA non uniform evaluation model is based on the theory of DEA (Data Envelopment analysis) theory. The transfer efficiency of subway station, taxi and bus in Xi′an railway station are researched and evaluated.
high-speed rail station; DEA model; transfer efficiency; transfer method
2016-11-30
原静(1992-),女,陕西渭南人,在读硕士研究生,主要从事交通规划方面的研究.
10.3969/i.issn.1674-5403.2017.01.014
U491
A
1674-5403(2017)01-0048-04

