上海青菜价格短期预测模型的比较研究

王美凤，赵京音*，邵 芳，张向飞，王美芳，杨 娟，钱婷婷，郑秀国

（1上海市农业科学院农业科技信息研究所，上海数字农业工程技术研究中心，上海 201403；2上海市农业委员会信息中心，上海 200335；3上海蔬菜集团，上海 201824）

上海青菜价格短期预测模型的比较研究

王美凤1，赵京音1*，邵 芳2，张向飞2，王美芳3，杨 娟1，钱婷婷1，郑秀国1

（1上海市农业科学院农业科技信息研究所，上海数字农业工程技术研究中心，上海 201403；2上海市农业委员会信息中心，上海 200335；3上海蔬菜集团，上海 201824）

为了增强对青菜价格的短期预见性，利用SARIMA模型、X-12-ARIMA模型、Holt-Winters乘法模型与双指数平滑模型，分别建立了上海市批发市场青菜月平均价格预测模型。研究表明：四种模型中，SARIMA模型预测的精确度较好，且优于这四种模型的组合模型，使用该模型对2015年1—8月上海市批发市场青菜月平均价格进行预测，发现预测值与实际值之间的误差总体在4.47%—28.11%，预测月份中约75%月份的预测误差在20%之内，平均误差为14.8%，价格波动幅度在可接受范围。

青菜价格；时间序列模型；短期预测；比较研究；上海市

随着生活水平的不断提升，饮食越来越丰富多样化，人们也更注重饮食的健康搭配，绿叶菜作为饮食搭配中营养价值较高且有益健康的代表，几乎成为每个家庭餐桌上的必备食材。对惯有“三天不见青，两眼冒金星”的上海人而言，更是如此。绿叶菜由于受自身季节生长、外部天气、生产成本与贮存条件及政府政策等多种因素影响，常会出现价格频繁波动的现象，这对居民生活造成了极大影响。以上海需求量最大的青菜为例，预测其价格变动，不仅对政府能采取措施进行适时调控与稳定居民生活水平有重要作用，而且可为上海其他蔬菜定价提供重要参考。

针对蔬菜价格波动的已有研究中，定性趋势性分析的较多，定量预测性分析的较少。定量分析中，时间序列模型应用又较多［1-6］，如宋长鸣等［5］运用X-12-ARIMA季节调整模型及ARCH类模型分析了白菜、西红柿、黄瓜、菜椒和四季豆价格的季节性波动特点与其短期变动特征，并探析了货币供应量对蔬菜价格长期趋势的影响。与之类似，卢素丽等［6］则基于2004—2011年上海市批发市场青菜、鸡毛菜、生菜、米苋四种常见蔬菜的月均价时间序列数据，使用SARIMA模型分别分析了这四种绿叶菜价格的预测效果。此外，面板向量自回归模型［7-8］与空间计量模型［9］及人工神经网络预测法［10-13］也都被运用在蔬菜价格预测研究中。总体而言，针对绿叶菜价格变动的研究采用单一模型分析的较多，运用不同预测模型比较分析的几乎没有，本研究主要参照王川等［4］的方法，拟采用多种预测模型为分析工具，对上海青菜月均价格进行预测研究，以期找出最优的上海青菜短期价格预测模型方法。

1 材料与方法

1.1 数据来源

本研究以上海青菜短期价格为预测对象，青菜月平均价格数据来源于上海市农委信息中心，根据上海农业网站农产品价格监测系统中发布的所有批发市场对应月份每日价格数据的算术平均值推算所得。建模数据样本期为2010年1月至2014年12月的青菜价格数据①无特殊说明时，下文中的青菜价格均指上海市所有批发市场下的青菜月平均价格。，共计60个样本，模型预测精度评价数据以2015年1月至2015年8月的青菜价格数据为实际对照值。

1.2 模型方法

首先，对上海青菜价格数据进行时间序列特征的分析判断，然后根据分析结果再选择合适预测模型。时间序列数据的基本特征检验包括季节性、平稳性、趋势性、异方差性等检验，使用EVIEWS 6.0软件进行分析。

季节性检验通常采用时间序列趋势图来判断，若趋势图是以年为周期变动，则时间序列具有季节变动特征。同时季节性检验还可从时间序列的相关系数来分析，当样本阶为12或12倍数时，相关系数值明显大于这些阶的附近值时，也可表明时间序列存在季节变动特征。

趋势性检验先在EVIEWS 6.0软件中采用CensusX-12乘法或加法方法对时间序列进行季节调整分解，可获得季节调整后的趋势循环序列，再运用H-P滤波法对获得的趋势循环序列进行趋势波动与循环波动序列分离，最后根据分离出的趋势波动图来观察序列变化趋势。

平稳性检验通过ADF单位根检验来判断，若时间序列ADF单位根检验的τ值大于1%（或5%或10%）水平下的临界值时，则在1%（或5%或10%）水平下接受原假设，时间序列为非平稳时间序列；反之，拒绝原假设，时间序列为平稳时间序列。

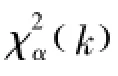
时间序列预测模型主要分线性与非线性两类，其中线性预测模型又包括ARCH模型、SARIMA模型；X-12-ARIMA模型、双指数平滑模型、Holt-Winter乘法模型等。其中自回归条件异方差模型（ARCH）适用于非平稳时间序列，且要求数据序列存在异方差问题。季节差分自回归移动平均模型（SARIMA模型）适用于具有非平稳与季节性特征但不存在异方差的时间序列。X-12-ARIMA模型（X12方法与ARIMA时间序列模型组合）适用于具有季节、随机、平稳等变动特征的时间序列。双指数平滑模型适用于具有线性趋势的时间序列。温特线性与季节性指数平滑法（Holt-Winter乘法季节调整模型）适用于具有线性趋势与季节等变化特征的时间序列。本文将根据对时间序列的特征分析结果，结合各模型适用条件选择合适模型对青菜价格进行预测分析。

2 结果与分析

2.1 上海青菜价格的特征分析

2.1.1 季节性特征

从图1看出，上海青菜价格整体呈现出以年为周期的变动特征，且青菜夏季的月平均价格几乎都在线性趋势线之上，甚至个别月份的青菜价格已高出线性趋势线1元（人民币，下同）左右（按斤计算）；为了能更清楚观察青菜价格的周期变动特征，将青菜价格进一步按季节月度平均值划分，则青菜的夏季月平均价均在趋势线之上（图2），这都表明青菜具有“夏淡”价较高的特征。另外，从青菜价格序列相关图（表1）观察，在样本K＝1、11、24等阶处，青菜价格序列自相关系数（AC）显著不为0，且数值也大于附近其他阶的数值。故序列趋势图与自相关系数均表明青菜价格存在季节性特征。

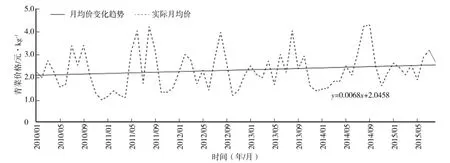
图1 2010—2015年上海市批发市场青菜月平均价格变化Fig.1 M onthly mean prices of Shanghaiwholesalem arkets’green vegetables in 2010—2015

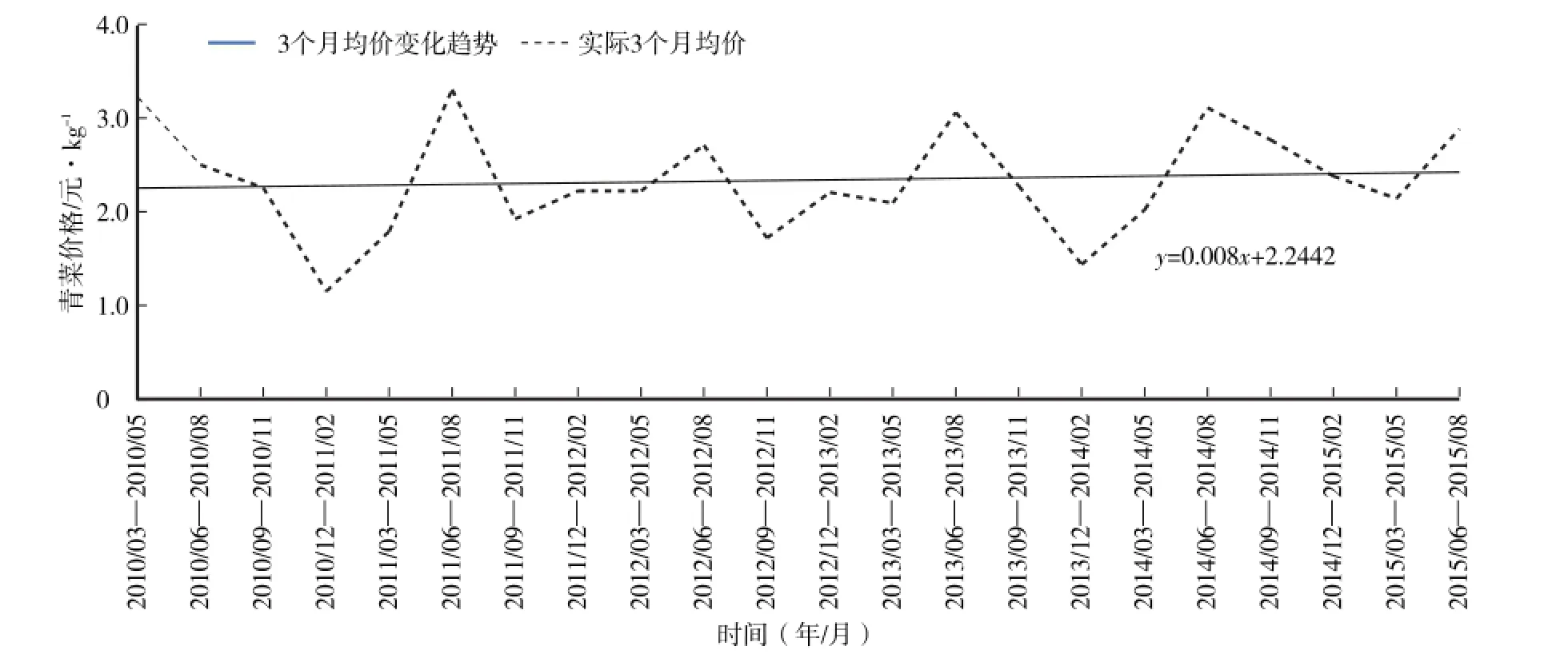
图2 2010—2015年上海市批发市场青菜3个月的平均价格变化Fig.2 Quarterly mean prices of Shanghaiwholesalemarkets’green vegetables in 2010—2015

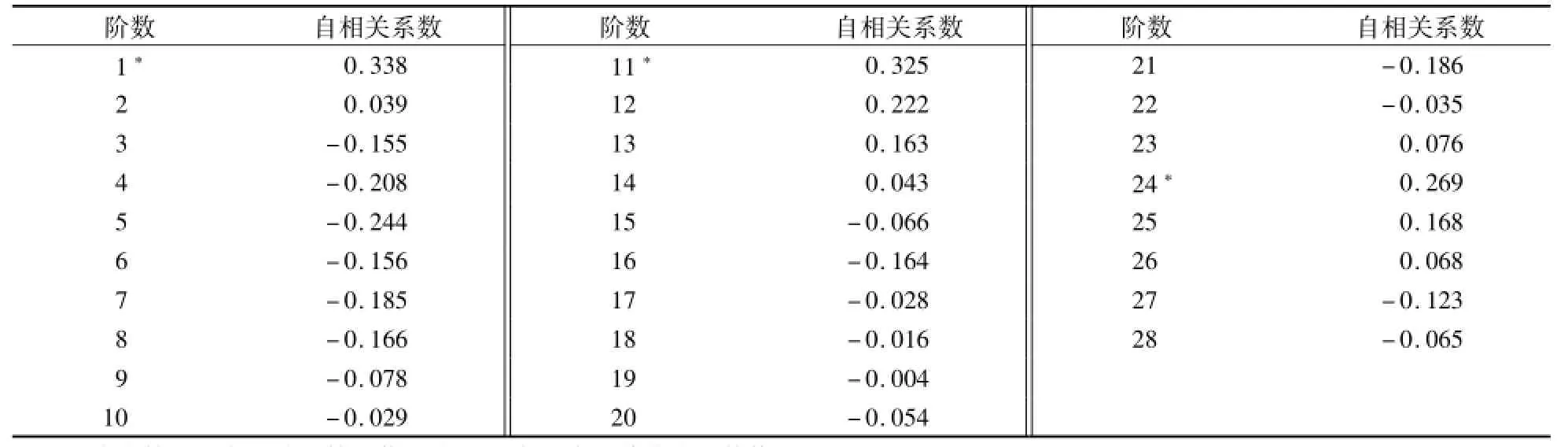
表1 上海市批发市场青菜月平均价格序列自相关系数Table 1 Autocor relation coefficients ofmonthly mean price series of green vegetables in Shanghaiwholesalem arkets

2.1.2 趋势性检验

从上海青菜价格趋势循环序列分解图（图3）中的趋势波动曲线来看，上海青菜价格呈现出缓慢上升变化趋势。

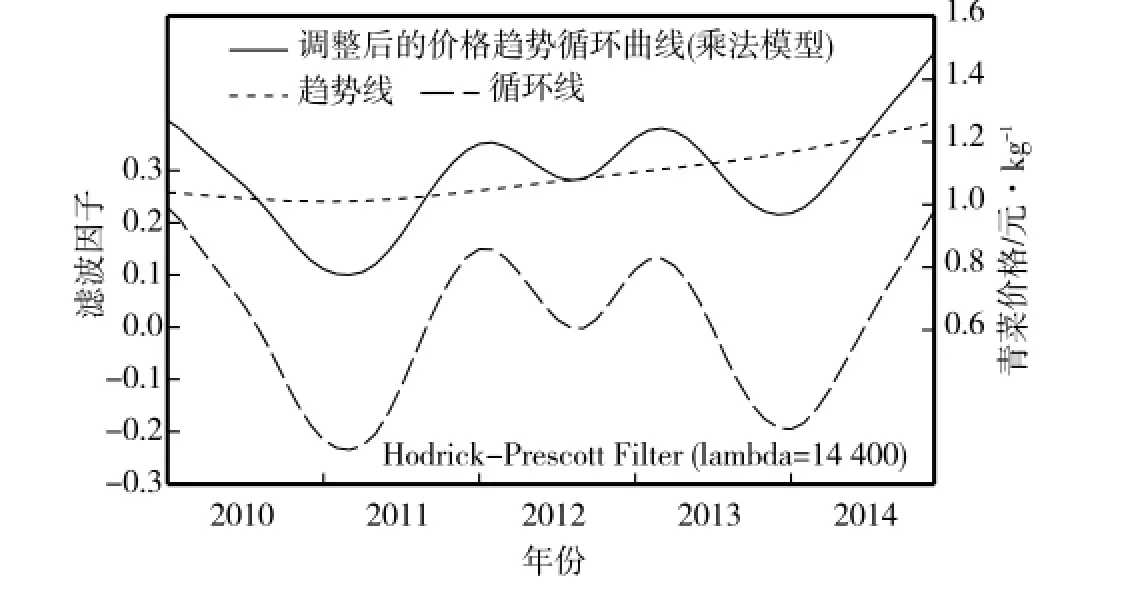
图3 2010—2014年青菜价格趋势循环序列分解图Fig.3 Periodic sequence decomposition chart of green vegetable price trend in 2010—2014

2.1.3 平稳性检验

采用ADF单位根检验青菜价格的平稳性，结果发现青菜价格序列ADF检验的τ值为－1.64，大于5%（或1%）水平下的临界值－1.95（或－2.60），故在5%（或1%）显著性水平下青菜价格为非平稳序列；而青菜价格一阶差分序列ADF检验的τ值为－10.00，小于5%（或1%）水平下的临界值－1.95（或－2.60），故在5%（或1%）显著性水平下青菜价格的一阶差分序列为平稳序列；因此青菜价格为一阶单整序列。这对SARIMA模型与ARIMA模型中一些参数的确定至关重要。

2.1.4 异方差检验

综上分析可知，青菜价格的波动呈现出了非平稳、上升与季节的变动特征，但不存在异方差。因此依据青菜价格序列的这些特征，选择时间序列模型中的SARIMA模型、X-12-ARIMA模型、Holt-Winter乘法模型与双指数平滑模型作为青菜价格的预测模型。

2.2 短期预测模型的应用

2.2.1 SARIMA预测模型的应用

应用ARIMA（p，d，q）（P，D，Q）S模型对青菜价格进行短期预测分析时，首先，根据此模型的参数识别方法确定模型的参数①WP在作季节差分之前进行了1阶差分，记为DWP，即WP为一阶单整序列，所以确定d＝1。首先，为消除青菜价格序列的季节波动变化，进一步对DWP作间隔12期的一阶差分，记为SDWP，但从SDWP的相关图与序列折线图知，SDWP的自相关系数与偏相关系数都显著不为零，样本阶在1、11、12等处的自相关、偏相关系数明显较大，故SDWP序列仍存在季节变动特征，但SDWP已为平稳序列。若继续对序列SDWP进行滞后12期的一阶差分，记为SSDWP，发现SSDWP序列的季节波动并没有明显改善，所以为方便建模考虑，只做一阶季节差分，由此可确定D＝1，S＝12。其次，根据SDWP相关图中的自相关系数与偏相关系数确定p＝1、2、3，q＝1。最后，由于SDWP序列的自相关、偏相关系数均不为零，所以选取P＝1，Q＝1。，即d＝1，D＝1，S＝12，p＝1、2、3，q＝1。其次，根据识别参数的几种组合，通过经验比较与适当调整模型，发现在5%显著性水平下带常数项ARIMA（2，1，1）（1，1，1）12模型的参数都通过了显著性检验②ARIMA（2，1，1）（1，1，1）12模型的Pro（C）＝0.0000，Pro（AR（1））＝0.0000，Pro（AR（2））＝0.0148，Pro（SAR（12））＝0.0482，Pro（MA（1））＝0.0000，Pro（SMA（12））＝0.0000，其中Pro代表伴随概率，Pro括号内代表模型变量。，残差也不存在序列相关③ARIMA（2，1，1）（1，1，1）12模型的杜彬-瓦特森统计量（D.W值）为2.006431，与2十分接近。，且满足白噪声过程④ARIMA（2，1，1）（1，1，1）12模型残差相关图中的自相关系数与偏相关系数都在置信区间内。，这都表明ARIMA（2，1，1）（1，1，1）12模型通过了检验⑤另外，ARIMA（2，1，1）（1，1，1）12模型滞后多项式的倒数根都在单位圆内，表明青菜价格序列在两次差分后平稳且可逆。，所以带常数项的ARIMA（2，1，1）（1，1，1）12模型较为理想⑥相比于其他参数的组合模型，ARIMA（2，1，1）（1，1，1）12模型不仅AIC值（0.995793）与SC值（0.757274）最小，而且R2也最大（可决系数R2＝0.467923，调整后的可决系数R2＝0.467923）。，具体函数为：

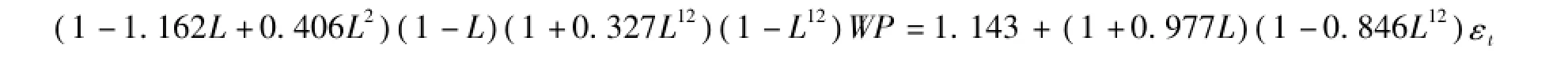
其中WP为青菜价格，εt表示第t月青菜价格的随机扰动项。最后，应用带常数项的ARIMA（2，1，1）（1，1，1）12预测模型对青菜价格走势进行短期预测，预测期为2015年1月—8月（表2）。从模型的预测价与实际价之间的相对误差绝对值来看，相对误差介于4.47%—28.11%，最大误差达28.11%，平均误差为14.8%。

2.2.2 X-12-ARIMA预测模型的应用

应用X-12-ARIMA模型对青菜价格进行短期预测分析时，需先对青菜价格原序列（WP）剔除季节性因素，再对剔除季节因素后的序列构建ARIMA模型，发现带常数项ARIMA（2，1，2）的模型较为合适①首先，带常数项ARIMA（2，1，2）模型的Pro（C）＝0.0000，Pro（AR（1））＝0.0000，Pro（AR（2））＝0.0000，Pro（MA（1））＝0.0000，Pro（MA（2））＝0.0000，其中Pro代表伴随概率，Pro括号内代表模型变量，表明在1%显著水平下ARIMA（2，1，2）模型的参数都通过了显著性检验。其次，ARIMA（2，1，2）模型的杜彬-瓦特森统计量（D.W值）为1.699744，与2也算接近，这表明残差不存在序列相关，而且模型残差相关图中的自相关系数与偏相关系数都在置信区间内，满足白噪声过程。再者，ARIMA（2，1，2）模型滞后多项式的倒数根都在单位圆内，表明青菜价格序列在两次差分后平稳且可逆。最后，相比于其他参数的组合模型，ARIMA（2，1，2）模型不仅AIC值（0.592814）与SC值（0.770438）较小，而且R2也较大（可决系数R2＝0.169113，调整后的可决系数R2＝0.106404。这些都表明带常数项的ARIMA（2，1，2）模型通过了检验，较为理想。，具体函数为：

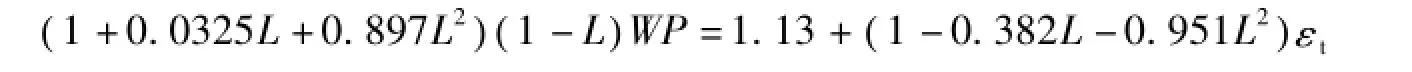
其中WP为青菜价格，εt表示第t月青菜价格的随机扰动项。将样本之外的2015年1—8月作为参照月，使用ARIMA（2，1，2）模型的预测值与相应月份的季节因子推算出青菜价格的预测值（表2），从模型预测价与实际价之间的相对误差绝对值发现，相对误差为1.15%—52.49%，最大误差达52.49%，平均误差为20.5%。

2.2.3 Holt-Winters乘法预测模型的应用

应用Holt-Winters乘法预测模型对青菜价格进行短期预测分析时，同样将样本之外的2015年1—8月作为参照月，预测结果见表2。从模型预测价与实际价之间的相对误差绝对值发现，相对误差为5.88%—55.55%，最大误差达55.55%，平均误差为20.0%。

2.2.4 双指数平滑预测模型的应用

应用双指数平滑预测模型对青菜价格进行短期预测分析时，同样将样本之外的2015年1—8月作为参照月，预测结果见表2。从模型预测价与实际价之间的相对误差绝对值发现，相对误差为3.89%—52.49%，最大误差达32.02%，平均误差为17.0%。

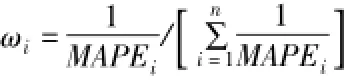
采用平均绝对百分比误差（MAPE）来评价比较分析不同模型的模拟效果，结果发现相比于其他模型与组合预测模型，SARIMA模型预测精确度最好，预测值与实际值间的误差为4.47%—28.11%，预测月份中约75%月份的预测误差在20%之内③根据“上海市人民政策办公厅关于印发上海市蔬菜应急保障供应预案的通知（5号，2011年）”知，绿叶菜平均批发价格偶有波动，上涨幅度在20%以内，全市绿叶菜供应就基本保持正常。这从侧面表明预测价格误差在20%之内时应属合理范围，是正常波动。，并且平均误差为14.8%④平均误差在50%之内的价格波动幅度属合理预测范围。，价格波动幅度在可接受范围。

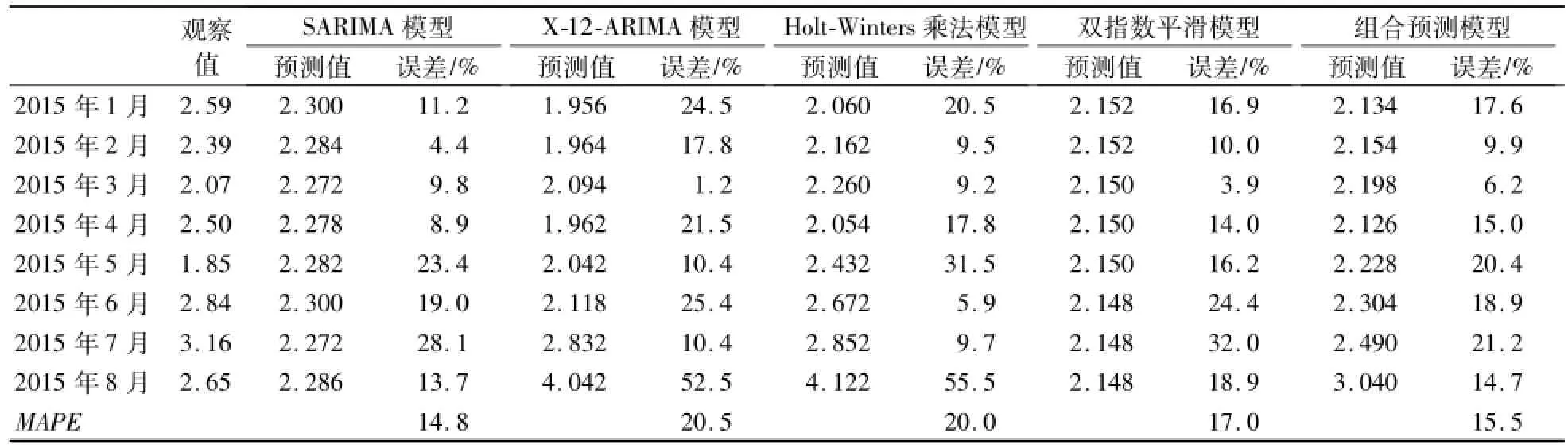
表2 青菜价格的观察值和不同模型下的预测值Table 2 Observed values of green vegetable prices and predicted values under differentmodels

3 结论与讨论

本文在对上海批发市场青菜月平均价格基本特征分析的基础上，根据分析结果对2010年1月至2014年12月的青菜月平均价构建不同短期预测模型，并对2015年1月至8月的青菜价格进行预测，研究发现：（1）青菜受自身生长条件、雨水、温度、突发性灾害天气与供求变动及饮食习惯等多种因素影响，既存在随机的特征，也存在季节的变化特征。青菜夏季月的平均价格整体相对较高，表现出明显的“夏淡”季节时价格高、波动频率大的特征。（2）通过对批发市场青菜月平均价格数据特征分析，选用SARIMA模型、X-12-ARIMA模型、Holt-Winters乘法模型与双指数平滑模型及其组合预测模型对青菜价格进行预测，发现相比于其他3种模型及4种模型的组合预测模型，SARIMA模型的预测效果较佳，预测精确度较好，预测值与实际值间的误差介于4.47%—28.11%，预测月份中约75%月份的预测误差在20%之内，同时平均误差为14.8%，价格波动幅度在可接受范围。

由于批发市场青菜月平均价格的影响因素较多，波动较为频繁，所以任何预测方法都无法产生绝对的准确结果，这不仅仅是模型方法本身的问题，更重要的是有诸多影响因素的变量数据获得较难或根本无法获得，甚至未来一些影响因素也难以预见。因此，在尽可能采集影响因素数据的基础上，继续探索模型方法提高模型预测的精度与准确预测青菜价格走势仍是未来研究的方向。不同模型均有自身一定的适用条件，对信息提取程度也会有所不同，所以对于其他种类的绿叶菜，即使有相同的基本特征，是否适用的最佳预测模型也相同？这也是未来有待进一步研究的方向。构建纳入多影响因素的绿叶菜价格预测模型也是未来研究的一个重点。此外，本文对应季青菜短期价格预测所采用的数据为月度平均数据，易导致预测结果精度不高，可能缺乏市场指导意义，所以对蔬菜类产品的日均价或周均价预测又是未来研究的重点之一。

［1］沈辰，穆月英.我国蔬菜价格的时间序列变动分析［J］.统计与决策，2011（16）：78-80.

［2］翟欣，黄丹枫.都市绿叶蔬菜价格波动原因与对策研究［J］.长江蔬菜，2012（14）：1-6.

［3］钱智，康芳华，张晔.上海市蔬菜价格持续上涨的成因及对策［J］.科学发展，2011（1）：53-59.

［4］王川，赵俊晔，赵友森.组合预测模型在农产品价格短期预测中的应用：以苹果为例的实证分析［J］.系统科学与数学，2013，33（1）：89-96.

［5］宋长鸣，李崇光.季节调整后的蔬菜价格波动：兼论货币供应量的影响［J］.统计与信息论坛，2012（3）：83-92.

［6］卢素丽，熊炳忠.上海绿叶菜价格时间序列建模分析［J］.上海农业科技，2012（2）：12-14.

［7］罗超平，李伟毅，翟琼.外部冲击对蔬菜价格波动的影响：基于面板向量自回归模型（PVAR）的实证分析［J］.中国蔬菜，2013（10）：16-22.

［8］罗超平，王钊，翟琼.蔬菜价格波动及其内生因素：基于PVAR模型的实证分析［J］.农业技术经济，2013（2）：22-30.

［9］王钊，姜松.我国蔬菜价格变动的空间计量分析［J］.农业技术经济，2013（11）：4-14.

［10］武舜臣.我国蔬菜价格波动的经济学分析及对策：基于蛛网模型［J］.决策与信息，2011（8）：158-159.

［11］王方舟.河北省蔬菜生产对价格变动的反应研究：基于经济学的蛛网模型检验［J］.湖北农业科学，2013，52（2）：463-467.

［12］罗长寿.基于神经网络与遗传算法的蔬菜市场价格预测方法研究［J］.科技通报，2011，27（6）：881-885.

［13］孙素芳，罗长寿.基于RBF神经网络的蔬菜价格预报研究［J］.中国农学通报，2011，27（28）：269-273.

（责任编辑：程智强）

Comparative study on short-term forecastmodels of green vegetable prices in Shanghai

WANG Mei-feng1，ZHAO Jing-yin1*，SHAO Fang2，ZHANG Xiang-fei2，WANG Mei-fang3，YANG Juan1，QIAN Ting-ting1，ZHENG Xiu-guo1
（1Agriculturɑl Informɑtion Institute of Scienceɑnd Technology，Shɑnghɑi Acɑdemy of Agriculturɑl Sciences；Shɑnghɑi Engineering Reseɑrch Center for Digitɑl Agriculture，Shɑnghɑi201403，Chinɑ；2Shɑnghɑi Agriculturɑl Commission Informɑtion Center，Shɑnghɑi200335，Chinɑ；3Shɑnghɑi Vegetɑbles Group，Shɑnghɑi201824，Chinɑ）

In order to improve the short-term foreseeability of green vegetable prices，models of forecasting monthlymean price of green vegetables in Shanghaiwholesalemarkets were established by using the SARIMA model，X-12-ARIMA model，Holt-Winters multiplication model and double exponential smoothing model respectively.The results showed that the forecast precision of the SARIMA model was the highest among the above models and also better than their combination models’.When the monthly mean prices of the green vegetables during January—August of 2015 were forecasted by the SARIMA model，the errors between the predicted and actualvalueswere generally 4.47%—28.11%and averagely 14.8%，and the errors of some75% forecasted months were less than 20%，being an acceptable range of price fluctuation.

Green vegetable price；Time seriesmodel；Short-term forecast；Comparative study；Shanghai

F323.7

A

1000-3924（2017）01-160-06

2016-01-29

上海市科技兴农重点攻关项目［沪农科攻字（2015）第2-6号］；上海市科委科研计划项目（15391900102）

王美凤（1984—），女，博士，助理研究员，主要从事农业信息技术研究。E-mail：wangmeifeng494494＠163.com

*通信作者，E-mail：zjy＠saas.sh.cn