北斗三频相位观测值线性组合研究

颜怀成，韩保民，张家新

山东理工大学 建筑工程学院，淄博 255049

北斗三频相位观测值线性组合研究

颜怀成，韩保民*，张家新

山东理工大学 建筑工程学院，淄博 255049

以北斗三频数据为基础，给出了北斗三频组合观测值的数学模型并系统分析了组合后的波长、电离层误差以及观测噪声误差；在保持整周模糊度整数特性的前提下，以整数线性变换法为基础，通过Matlab编程实现组合系数的优化选取。通过将不同组合系数应用于伪距相位法三频数据周跳探测中，发现组合系数之和不为0的组合周跳探测值均在0.5周以上，且组合系数之和越大，波动越大；通过将不同组合系数应用于无几何CIR法三频数据模糊度解算中，发现系数之和不为0,但波长较长的组合求得的模糊度残差值大致在0.6周，通过合适的模糊度搜索方法可以得到正确的模糊度固定解，在短基线模糊度解算中可以考虑使用。

北斗；三频数据；线性组合；整数线性变换；优化选取

北斗卫星导航定位系统(BeiDou Satellite Navigation System，BDS)是中国自主研发并与世界其他卫星导航系统兼容共用的全球卫星导航定位系统，该系统可在全球范围内全天候、全天时为用户提供高精度的快速定位、精密授时、短报文通信服务1-3]。北斗二代导航系统播发B1、B2、B3三个频点的信号，多频观测值能形成具有较长波长、较弱电离层延迟误差、较弱噪声误差等优良特性的组合观测值，有利于提高周跳探测与修复以及整周模糊度解算的精度，从而获得高精度的导航定位结果4-5]。

随着多频技术的不断发展，国内外学者对三频组合观测理论进行了大量的研究。文献6]给出了Galileo四频整系数组合观测量的定义，并分析了相关误差影响；文献7]提出了无几何模式的三频无电离层组合观测值，该组合观测值消去了一阶电离层影响以及几何距离影响，适用于周跳探测；文献8]不仅研究了整系数组合观测量，还对实系数组合进行了深入研究。

本文以北斗三频组合观测值为基础，分析了北斗三频数据线性组合系数的优化选取问题；将不同组合系数应用于伪距相位法三频数据周跳探测和无几何CIR法三频数据模糊度解算中，通过实例分析了不同组合系数的性能与适用范围，对北斗三频数据处理过程中组合系数的选取有一定的指导作用。

1 北斗三频组合观测量的定义

假设北斗三频载波频率依次为f1、f2、f3，且满足f1>f3>f2。北斗卫星导航系统3个频率的载波相位观测方程可表示为(以周为单位)：

(1)

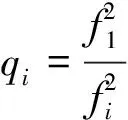
假设组合观测值系数分别为i，j，k，则载波相位组合观测值可表示为：

(2)

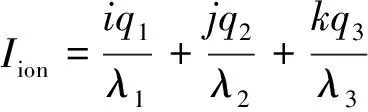
2 组合观测值误差特性分析

2.1 组合波长

北斗卫星导航系统的基准频率f0=2.046 MHz，导航定位所用的频率由基准频率生成，各个频点的频率可表示为fi=nif0。结合北斗三频数据可知n1=763，n2=590，n3=620，组合观测值的频率可以表示为：

(3) 为了保持组合观测值模糊度的整数特性，i，j和k都为整数。由整数线性方程解存在理论得9]：

(4)

式中：gcd (n1,n2,n3)表示括号内3个数的最大公约数；Kijk是由i，j，k决定的整数。

可知，北斗导航系统的gcd (n1,n2,n3)=1，则组合波长为：

(5)

因为λ0的值是固定的，所以组合波长的大小由Kijk值的大小决定。Kijk可作为表征波长大小的参数，定义其为巷数10]。

2.2 电离层延迟误差

以周为单位的电离层延迟系数为：

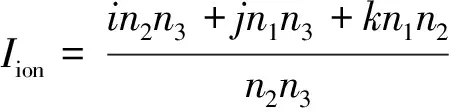
(6)

根据整数线性方程解存在理论可得9]：

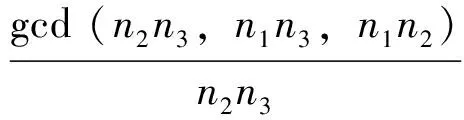
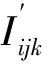
(7)

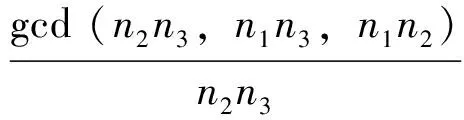
2.3 观测噪声误差

由εφc=iεφ1+jεφ2+kεφ3并根据误差传播理论可知，以周为单位的载波相位组合观测量的测量噪声可表示为：

(8)

式中：σφ1、σφ2、σφ3分别为以周为单位的各频率载波测量噪声标准差。

假设各载波观测量间独立且标准差σφ1=σφ2=σφ3=σε，则式(8)可写为：

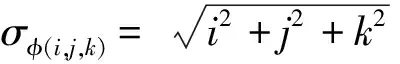
3 北斗三频组合观测值的选取

对于周跳探测、模糊度解算等问题，一般要求载波相位组合观测值满足以下几个条件：1)组合系数i，j，k均为整数，保证模糊度的整数特性；2)有较长的波长；3)较弱电离层延迟误差；4)低观测噪声误差11]。

前文已经保证i，j，k为整数，在此前提下，条件2)～4)即要求由组合系数决定的参数Kijk、Iijk、η′较小。

3.1 整数线性变换

将式(4)、式(7)写成矩阵形式：

(10)

式中：g1=gcd (n1,n2,n3)，g2=gcd (n2n3,n1n3,n1n2)。由式(10)可知，组合系数i，j，k确定后，Kijk、Iijk值确定；但对于确定的Kijk、Iijk，组合系数却有无穷多组。因此，为了从特定Kijk、Iijk的无穷多组系数组合中选出噪声系数η′最小的组合，需要定义第3个整数线性变换。参照文献12]，本文取第3个线性变换为i+j+k=Sijk，则式(10)转换为：

(11)

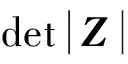
(12)

式中：Z*为Z的伴随矩阵;L、I和S分别为Z*矩阵中的3个列向量。

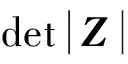
(13)

根据上述分析可知，对于给定的Kijk、Iijk值以及合适的Sijk值，能得到确定的整数系数i，j，k。

3.2 最优组合观测值系数选取

实际需要的是在给定Kijk、Iijk的条件下，选取最优组合观测值使以周为单位的噪声系数η′最小。令H=L·Kijk+I·Iijk，则有：

(14)

将式(14)对Sijk进行求导，并令导数值为零得：

(15)

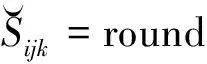
对于北斗导航系统而言，代入数据得：

(16)

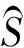
从上述分析可知，对于有较长波长、较弱电离层延迟且噪声最优的组合，其组合系数和Sijk为0。

将Kijk作为自变量，Iijk作为因变量对式(16)进行变换：

(17)

根据式(17)可以在Kijk、Iijk平面内绘出对应于不同Sijk值的最小噪声轴分布图，且不同Sijk取值的直线沿着通过零点的直线Iijk=-61.104Kijk对称分布。考虑Sijk的整数特性，

Kijk、Iijk平面内Sijk分别取0，±1,2时的最小噪声轴分布如图1所示。

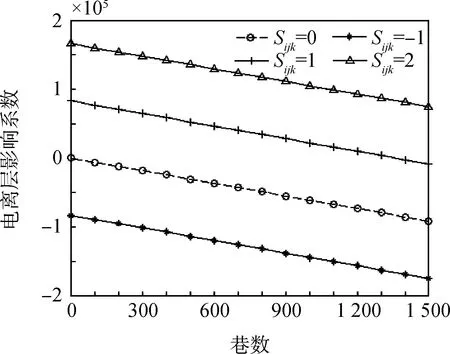
图1 北斗三频最小噪声轴分布Fig.1 Minimum axial distribution noise of BDS

从图1可以看出，以周为单位的电离层延迟系数Iijk随着组合系数之和的增大而增大；具有较弱电离层误差、较小噪声系数超宽巷组合的系数之和为0；具有较弱电离层误差、较小噪声系数的窄巷组合的系数之和为1。

3.3 计算与分析

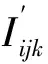
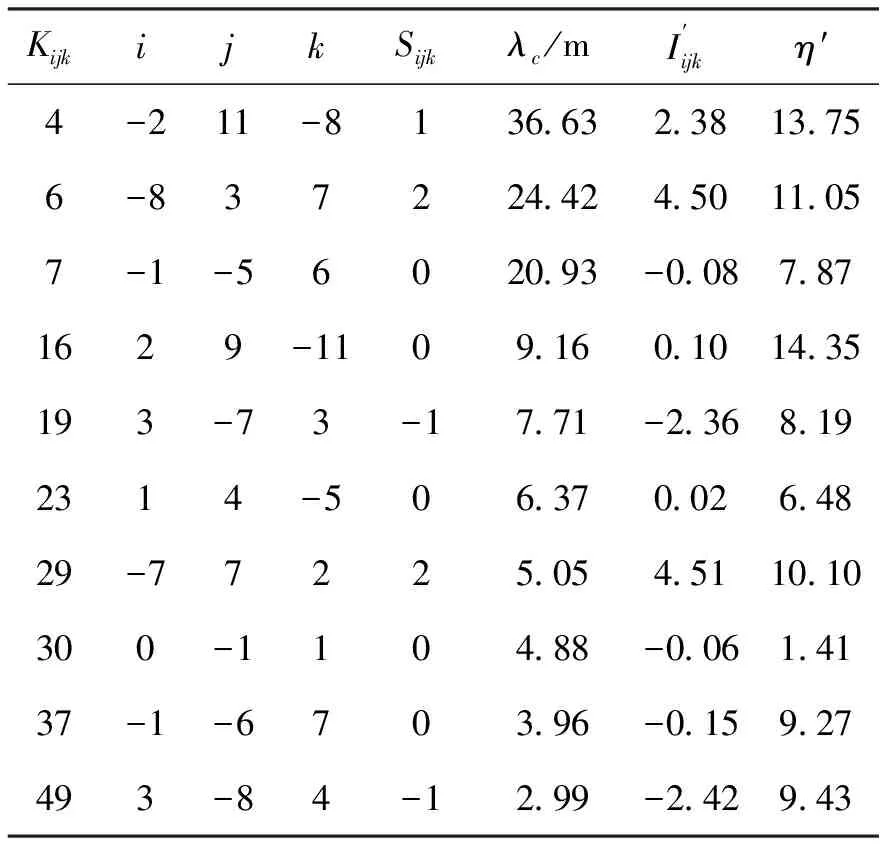
表1 北斗超宽巷组合

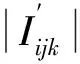
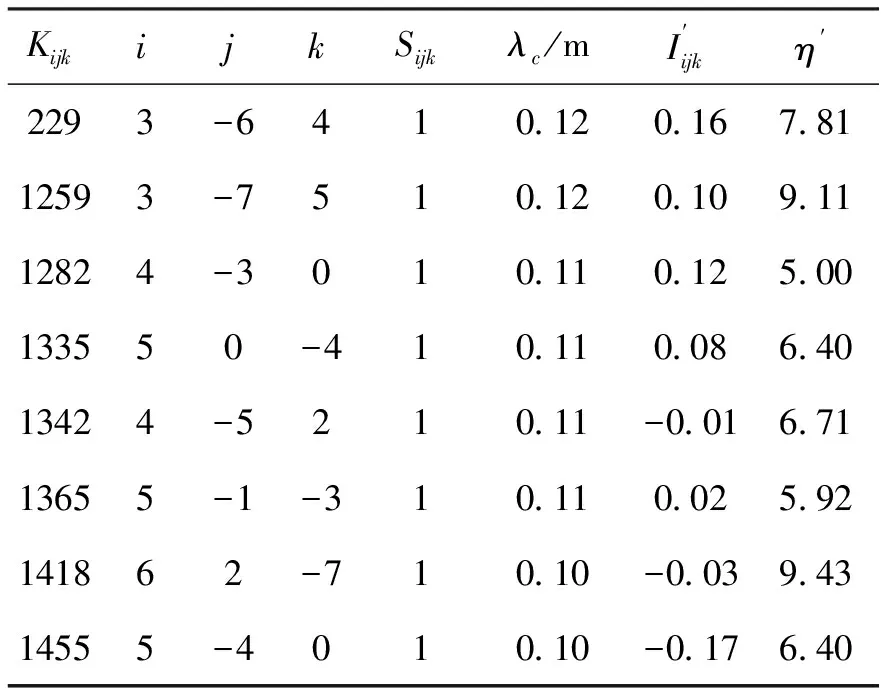
表2 北斗窄巷组合

分析表1和表2，可以看出：

1)表1中列出的组合系数之和为0的超宽巷组合，其电离层延迟系数和噪声系数均较小，适用于解算中长基线的模糊度13-14]，如组合(0，-1，1)、(-1，-5，6)；而对于组合系数之和不为0的超宽巷组合，电离层延迟系数和噪声系数对周跳探测和模糊度解算的影响较大，因此只适合于短基线的周跳探测。

2)表2中的组合虽然波长较短，但电离层延迟系数却较小，绝对值均小于0.3，且噪声误差也较小。其中组合(4，-5，2)、(5，-1，-3)的电离层延迟系数很小，在中长基线相对定位相关性较弱的情况下，是较好的组合观测值选择。

4 实例分析

为了验证上述结论，选取表1中三组系数之和不同的组合，将其应用于伪距相位法三频数据的周跳探测中。实验数据为2014年7月31日采用司南接收机采集的一组北斗静态三频数据，采集地点为中国广东省广州市天河区，采样间隔10s，卫星高度角大于10°，观测时间为3.5h，共计1260个历元。

实验采用C02号卫星的伪距和载波相位观测值作为实验数据，经检测原始载波相位观测数据中不存在周跳，因此理论周跳检测值为0。不失一般性，实验分别选取系数和为0的组合(0，-1，1)、系数和为1的组合(-2，11，-8)以及系数和为2的组合(-8，3，7)进行周跳探测，探测结果如图2所示。

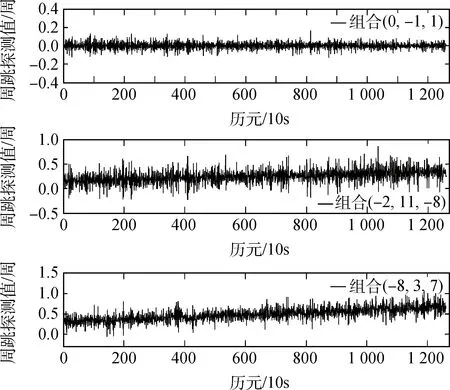
图2 周跳探测结果Fig.2 Results of cycle-slip detection

从图2可以看出，系数之和为0的超宽巷组合(0，-1，1)周跳探测值均在0.2周内，能准确地探测出周跳；而组合系数之和不为0的组合周跳探测值均在0.5周以上，且组合系数之和越大，波动越大，从而导致探测的周跳严重偏离周跳真值。因此，在三频数据的周跳探测中不建议使用系数之和不为0的组合。

考虑到波长较长的组合更适用于整周模糊度的解算15]，选取表1中系数之和不为0但波长较长的组合，将其应用于无几何CIR法三频数据的整周模糊度解算中，以验证系数和不为0但波长较长的组合是否适用于三频数据的整周模糊度解算。

实验以C02-C03卫星的双差观测值为基础，选取组合系数和为0的组合(0，-1，1)以及系数和不为0但波长较长的组合(-2，11，-8)、(-8，3，7)进行整周模糊度解算。利用所有历元数据解算出模糊度的整数解，然后用每个历元的模糊度浮点解减去整数解得到残差，3个组合的残差结果如图3所示。

从图3可以看出，系数之和为0的超宽巷组合(0，-1，1)求得的模糊度残差值在0.2周以内，即模糊度单历元取整就可得到正确的固定解；系数之和不为0但波长较长的组合(-2，11，-8)、(-8，3，7)求得的模糊度残差值稍大，大致在0.6周左右，通过合适的模糊度搜索方法可以得到正确的模糊度固定解。

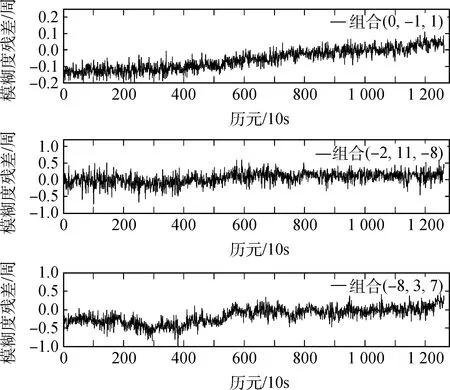
图3 模糊度残差值Fig.3 Residual value of the ambiguity

5 结束语

通过上述分析，可以得出结论：

1)北斗三频相位组合观测值中，具有较弱电离层误差、较小观测噪声的超宽巷组合的系数之和为0；具有较弱电离层误差、较小观测噪声误差的窄巷组合的系数之和为1。

2)以周为单位的电离层延迟系数随着组合系数之和的增大而增大。

3)在三频数据的周跳探测中，电离层延迟与观测噪声为主要影响因素，此时系数之和为0的组合能较好地应用于周跳探测中，如(0，-1，1)、(-1，-5，6)组合；而组合系数之和不为0的组合则会导致周跳的误探，在三频数据的周跳探测中不建议使用。

4)系数之和不为0的组合的电离层误差、观测噪声误差要大于系数之和为0的组合，但其在波长较长的情况下，通过适当的模糊度搜索方法可以得到正确的模糊度固定解，在短基线模糊度解算中可以考虑使用。

References)

[1] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战J]. 测绘学报, 2010, 39(1):1-6.

YANG Y X.Progress,contribution and challenges of Compass/Beidou satellite navigation systemJ]. Acta Geodaetica et Cartographica Sinica，2010,39(1):1-6(in Chinese).

[2] 杨元喜, 李金龙, 王爱兵,等. 北斗区域卫星导航系统基本导航定位性能初步评估J]. 中国科学:地球科学, 2014(1):72-81.

YANG Y X，LI J L，WANG A B，et al.Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite systemJ]. Science China:Earth Sciences,2014(1):72-81(in Chinese).

[3] 崔红正, 唐歌实, 宋柏延,等. 北斗卫星导航系统实时定轨与钟差处理策略J]. 中国空间科学技术, 2015, 35(5):1-7.

CUI H Z，TANG G S，SONG B Y，et al.BDS satellite real time orbit and clock determination and initial results analysisJ]. Chinese Space Science and Technology，2015, 35(5):1-7 (in Chinese).

[4] 何俊, 刘万科, 张小红. 北斗短基线三频实测数据单历元模糊度固定J]. 武汉大学学报(信息科学版), 2015, 40(3):361-365.

HE J，LIU W K，ZHANG X H.Singal epoch ambiguity resolution of BDS triple frequence measured data under short baselineJ]. Geomatics and Information Science of Wuhan University，2015, 40(3):361-365(in Chinese).

[5] 元荣, 白征东, 过静珺. 基于TCCAR的北斗三频相对定位J]. 大地测量与地球动力学, 2014, 34(4):106-109.

YUAN R，BAI Z D，GUO J J.Beidou triple-frequency relative positioning based on TCCAR methodJ]. Journal of Geodesy and Geodynamics，2014, 34(4):106-109 (in Chinese).

[6] 王泽民, 柳景斌. Galileo卫星定位系统相位组合观测值的模型研究J]. 武汉大学学报(信息科学版), 2003, 28(6):723-727.

WANG Z M，LIU J B.Model of inter-frequency combination of Galileo GNSSJ]. Geomatics and Information Science of Wuhan University，2003, 28(6):723-727 (in Chinese).

[7] SIMSKY A. Three′s the charm, triple-frequency combinations in future GNSSJ]. 2006, 1(5):38-41.

[8] 李金龙, 杨元喜, 何海波,等. 函数极值法求解三频GNSS最优载波相位组合观测量J]. 测绘学报, 2012, 41(6):797-803.

LI J L，YANG Y X，HE H B，et al.Optimal carrier-phase combinations for triple-frequency GNSS derived from an analytical methodJ]. Acta Geodaetica et Cartographica Sinica，2012, 41(6):797-803(in Chinese).

[9] NATHANSON M B. Elementary methods in number theoryM].北京： 世界图书出版公司, 2003.

[10] COCARD M, BOURGON S, KAMALI O, et al. A systematic investigation of optimal carrier-phase combinations for modernized triple-frequency GPSJ]. Journal of Geodesy,2008, 82(9):555-564.

[11] 郭忠臣, 高井祥, 王坚,等. GNSS多频观测值线性组合研究J]. 大地测量与地球动力学, 2015, 35(3):379-382.

GUO Z C，GAO J X，WANG J，et al.Research on multi-frequency observation linear combination of GNSSJ]. Journal of Geodesy and Geodynamics，2015, 35(3):379-382 (in Chinese) .

[12] 刘国超, 黄张裕, 徐秀杰,等. 北斗三频数据线性组合优化分析J]. 测绘科学, 2015, 40(10):69-73.

LIU G C，HUANG Z Y，XU X J，et al.Systematic investigation of optimal carrier-phase combinations for triple-frequency BDSJ].Science of Surveying and Mapping，2015, 40(10):69-73 (in Chinese).

[13] 申俊飞, 何海波, 郭海荣,等. 三频观测量线性组合在北斗导航中的应用J]. 全球定位系统, 2012, 37(6):37-40.

SHEN J F，HE H B，GUO H R，et al.Application research of linear combination based on triple-frequency observationJ].GNSS World of China，2012, 37(6):37-40 (in Chinese) .

[14] 张晨晰, 党亚民, 王潜心,等. 北斗三频组合在数据预处理中的应用J]. 测绘通报, 2014(10):1-6.

ZHANG C X，DANG Y M，WANG Q X，et al.The application of multi-frequency combination observation in BDS data preprocessingJ].Bulletin of Surveying and Mapping，2014(10):1-6(in Chinese).

[15] 李金龙. GNSS三频精密定位数据处理方法研究D]. 郑州：解放军信息工程大学, 2011.

LI J L.Researches on the algorithms of GNSS triple frequency precise positioningD].Zhengzhou:PLA Information Engineering University，2011 (in Chinese).

(编辑：高珍)

Research on triple-frequency carrier-phase observation linear combination of BeiDou satellite navigation system

YAN Huaicheng，HAN Baomin*，ZHANG Jiaxin

SchoolofArchitectureandEngineering，ShandongUniversityofTechnology，Zibo255049，China

The mathematical model of BeiDou triple-frequency carrier-phase linear combination was given based on BeiDou satellite navigation system triple-frequency data, and the wavelength, ionospheric error and the observation noise of linear combination were analyzed systemmatically. In terms of ambiguity integer properties and used the integer linear transformation method as a basis, the optimization of the combination coefficient was realized by Matlab.By applying different combination coefficients to the cycle-slip detection based on code-phase, it shows that the combined cycle slip detection with the sum of the combination coefficients being not 0,is more than 0.5 weeks, and the larger the sum of the combination coefficients is, the greater the fluctuation is. By applying different combination coefficients to the ambiguity resolution based on GF-CIR for triple-frequency observations, it shows that the residual value of ambiguity obtained by the combination of non-zero coefficients but long wavelengths are about 0.6 weeks.The correct ambiguity fixed solution can be obtained by the appropriate ambiguity search method,and this kind of coefficients can be used in short baseline ambiguity resolution.

BeiDou satellite navigation system；triple-frequency；linear-combination；integer linear transformation；optimization

10.16708/j.cnki.1000-758X.2017.0019

2016-06-28；

2016-12-08；录用日期：2017-01-24；

时间：2017-02-16 18:44:26

http:∥www.cnki.net/kcms/detail/11.1859.V.20170216.1844.012.html

国家自然科学基金资助项目(41074001)

颜怀成(1992-)，男，硕士研究生，1731768556@qq.com，研究方向为GNSS精密定位

*通讯作者：韩保民(1969-)，男，教授，hanbm@sdut.edu.cn，研究方向为GPS精密定位、低轨卫星精密定轨等

颜怀成,韩保民,张家新.北斗三频相位观测值线性组合研究J].中国空间科学技术, 2017,37(1)：104-110.YANHC,HANBM,ZHANGJX.Researchontriple-frequencycarrier-phaseobservationlinearcombinationofBeiDousatellitenavigationsystemJ].ChineseSpaceScienceandTechnology, 2017,37(1)：104-110(inChinese).

P228.4

A

http:∥zgkj.cast.cn