基于线性叠加技术的四倍频单片设计

王亚冰，何庆国，胡志富

(中国电子科技集团公司第13研究所 模型室，河北 石家庄 050051)

基于线性叠加技术的四倍频单片设计

王亚冰，何庆国，胡志富

(中国电子科技集团公司第13研究所 模型室，河北 石家庄 050051)

针对传统无源四倍频器需要两级二倍频级联且变频损耗较大等问题，利用线性叠加技术，研制了40 GHz单级无源四倍频单片。采用平面环形巴伦与正交混合网络相级联的方式，设计了四路移相功分结构，实现了基波和其他无用谐波的抑制，简化了电路设计，降低了倍频损耗。根据设计仿真结果，完成了四倍频器的流片与测试工作。实测结果表明，在20 dBm的驱动功率下，最大输出功率为-2.7 dBm。

四倍频；线性叠加；单片电路

随着系统工作频率的提高，毫米波和亚毫米波信号源在通信、雷达等领域具有越来越广泛的应用前景。目前，国际上主要依靠倍频器实现稳定的高频信号源，其具有降低毫米波系统的主振频率、扩展工作频段、获取稳定相噪特性等特性[1]。利用半导体器件非线性特性，可获得频率为基波频率倍数的射频源[2]。随着倍频次数增加，倍频器的变频损耗会急剧增大。因此，传统的无源四倍频器大多采用二倍频器-放大器-二倍频器结构[3-5]，即在两级倍频器之间插入一级驱动放大器，以减小倍频造成的插入损耗。

线性叠加技术[6]，不依靠器件的非线性。通过对四路输入信号进行半波整流并使其依次产生 的相位差，从而直接合成出四倍频信号。在叠加过程中，基波和其他无用谐波可得到较好的抑制，理论上倍频效率较高。本文介绍了一种基于线性叠加技术的无源四倍频单片的研制方法。

1 线性叠加倍频器的原理

倍频单片的设计采用了线性叠加技术，线性叠加技术的原理如下：假设有n列正弦波，这 列正弦波的角频率均是ω0，其依次具有2π/n的相位差，满足这些条件的n列波经过半波整流后，叠加在一起，即可合成出nω0的输出信号。下面以四倍频为例(即 )，对该原理进行分析，图1显示了这种叠加过程。图1(a)中四列波的角频率均是ω0，根据前文公式可知，其依次相差了2π/4=90°的相位差表达式为

IIp=I0sin(ω0t)

(1)

IQp=I0sin(ω0t+π/2)

(2)

IIm=I0sin(ω0t+π)

(3)

IQm=I0sin(ω0t+3π/2)

(4)

这4列波经过半波整流后，每列波横轴下方的波形消失，只留上方的波形，形成了图1(b)所示的类似脉冲余弦的半波信号。这4列半波信号相互叠加即能合成出所需的4ω0信号，实现四倍频，如图1(c)所示，具体的运算过程如下。

图1 线性叠加过程图

首先，IIP和IIm两列波，其角频率相同，但位相相差180°，经过图1(b)所示的半波整流过程后，叠加在一起，明显可得到图1(c)中的一列波IA，IA表达式即为

IA=I0|sin(ω0t)|

(5)

同理，剩余的另两列半波叠加得到了图1(c)中另一列波IB，IB表达式即为

IB=I0|cos(ω0t)|

(6)

将IA和IB线性叠加，可得IC

(7)

将|sin(ω0t)|和|cos(ωt)|的傅里叶级数的三角函数展开得到

(8)

(9)

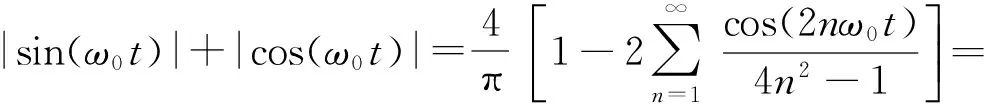
(10)

经过推导分析可知，四列基波线性叠加之后，可产生4ω0的输出信号，4ω0信号对应电流幅值为8/15π，据此可算出采用线性叠加方式制作的四倍频器的倍频效率为

(11)

即变频损耗约为-15.4 dB，同时输出端省去了滤波器的设计，简化了电路的设计。

2 四倍频器设计方案

倍频单片的电路原理框图如图2所示。

图2 40 GHz倍频单片电路原理框图

基波从输入PAD输入，经过四路移相功分器之后，产生了四列依次具有 相位差的波，这4列波经过二极管半波整流后，便可按照前文推倒的叠加过程进行线性叠加，直接产生四倍频信号。

2.1 移相功分电路的设计

实现前文所述的线性叠加方法，首先要产生四列具有相位差的基波信号。本文采用了平面环形巴伦[7]和正交混合网络[8-9]级联的方式，实现了信号的4路功分，同时4路输出信号依次相差90°的相位。如图3所示，输入基波信号由输入pad进入巴伦级，在节点1和节点2处，信号等幅且反相。之后，分别级联完全相同的正交混合网络，即可在端口1～4输出4列等幅且依次具有90°相位差的信号。

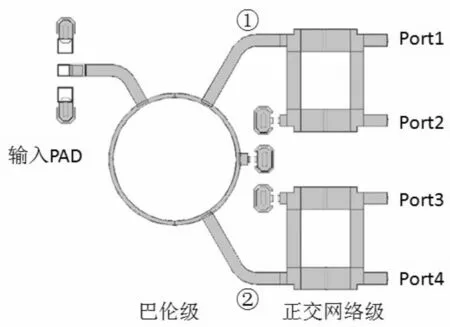
图3 移相功分器设计版图

通过版图设计布局，使输出端口呈严格的对称结构，这保证了在级联过程中的精确性。

2.2 半波整流

半波整流是线性叠加过程中不可缺少的步骤。为了产生较好的整流效果，要求二极管具有较短的反向恢复时间及较小的结电容。肖特基二极管以半导体-金属为依托，与普通二极管相比，肖特基二极管是多数载流子器件，无少数载流子存储效应。当加在肖特基结上的正向导通电压断开时，肖特基结将会在非常短的时间内建立起内建电势，以阻止电子由半导体向金属阳极的迁移。因此，反向恢复的电荷接近于零，这将大幅缩短二极管的反向恢复时间，利于二极管的工作频段向频率高端扩展[10]。

本文中肖特基二极管采用高电子迁移率的GaAs pHEMT工艺制作完成，肖特基二极管结构可由HEMT改进而来，栅极作为二极管的正极，HEMT的源极和漏极相连作为二极管的负极。二极管设计版图如图4所示。

图4 肖特基二极管版图

通过对二极管测试并拟合I-V曲线等工作，建立二极管模型，并在ADS软件中进行仿真设计。提取的零偏下的结电容的容值约为37 pF，二极管导通电压为0.8 V。通过对该二极管模型进行仿真实验，发现当输入频率为10 GHz时，输出的时域波形并不是一个理想的半波，这是因所选二极管受其结电容及反向恢复时间的影响，在时间轴的下方仍能看到电流过冲的现象，如图5所示。

图5 二极管整流后输出时域波形图

3 四倍频器测试结果

通过矢量网络分析、微波探针台、功率放大器、频谱仪等搭建了一套在片测试系统。图6和图7分别为四倍频单片的频谱测试结果和变频损耗测试结果。

图6 四倍频器输出频谱

从上图中可看出，在输入功率为20 dBm，输入频率为10 GHz测试条件下，倍频器基波和三次谐波的抑制度>20 dBc，二次谐波的抑制度>15 dBc。在9.6～10.4 GHz的输入频率范围内，无源四倍频器的变频损耗<24.5 dB，在10 GHz处输出功率最大，为-2.7 dBm，且频带内的输出平坦度较好。

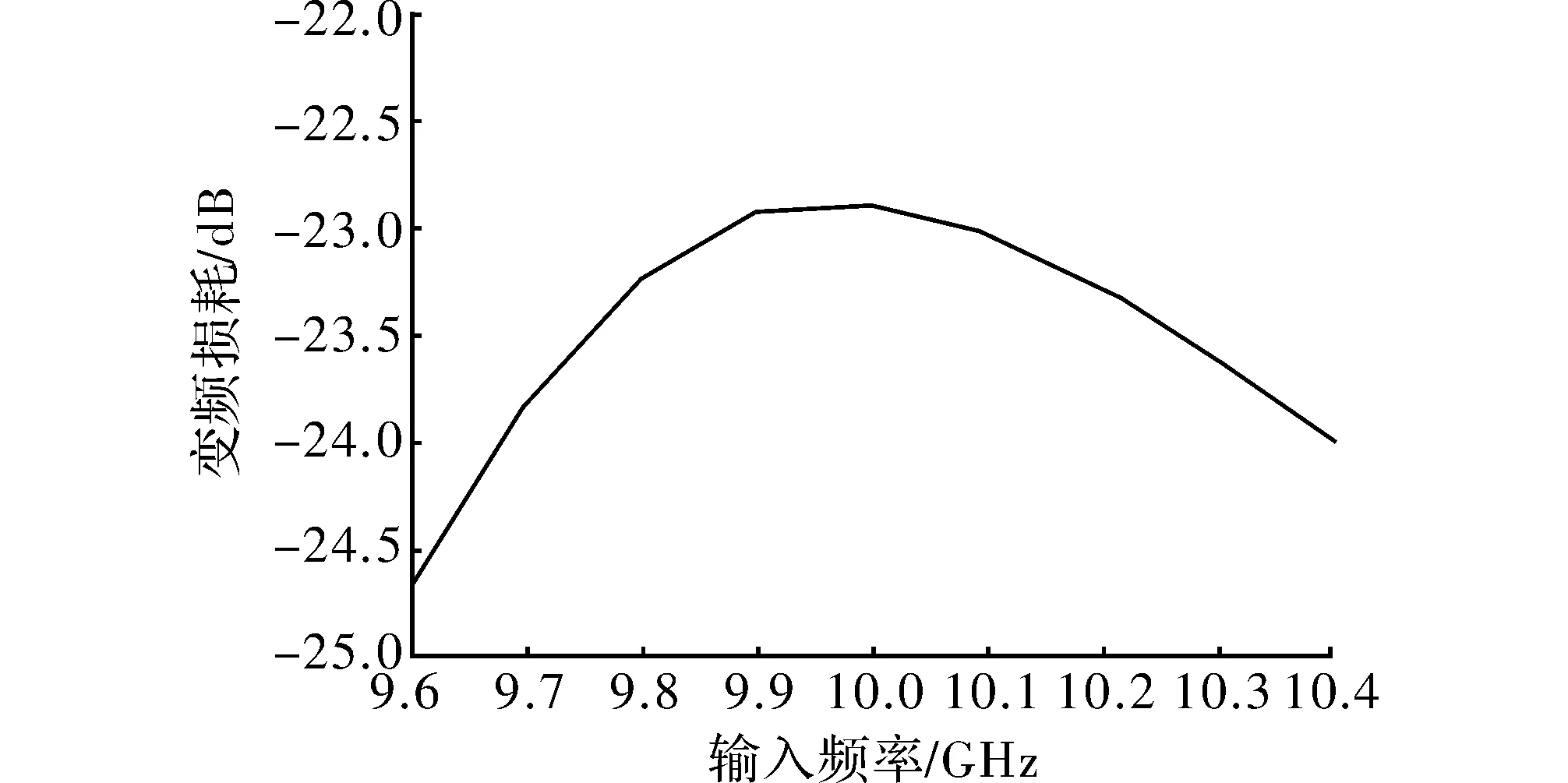
图7 四倍频器变频损耗测试结果

4 结束语

本文主要研究了基于线性叠加技术的无源四倍频单片的设计。采用了平面环形巴伦和正交混合网络级联的方式，实现了基波和无用谐波的高抑制度，且变频损耗较小。传统倍频器为了提高输出功率，在倍频之后接放大器，放大器频段需要满足倍频之后的频率，而本设计可将功放器件接于整流二极管之后，放大器频段只需满足基波频率即可，这一点对更高频率乃至太赫兹倍频器的设计具有指导意义。

[1] 王抗旱.宽带毫米波四倍频器[J].半导体技术,2012,37(3):228-230.

[2] 黄香馥.微波固体电路[M].成都:成都电讯工程学院出版社,1988.

[3] 彭文峰. Ka波段宽带四倍频器的研制[J]. 电子工程师,2003,29(12):56-59.

[4] 税兰英.Q波段宽带四倍频器的研制[D].成都:电子科技大学,2007.

[5] 梁木生,唐小宏,李金艳.Ka波段微带四倍频器研制[J].电子科技大学学报,2008,37(S1):79-81.

[6] Huang Daquan,Tim R.LaRocca.324GHz CMOS frequency generator using linear superposition technique[C].Xi’an:ISSCC,2008.

[7] 汤利霞,于洪喜.平面巴伦的理论分析[J].空间电子技术,2009,6(1):83-91.

[8] Moselhy A M，Nassar A M，Gazza M A E.Analysis and design of microstrip power divider[J].IEEEX plore International Symposium on Signals, Systems, & Electronics Issse, 1995(2):545-548.

[9] David M Pozar.微波工程[M].3版.张肇仪,周乐柱,吴德明,等,译.北京:电子工业出版社,2006.

[10] 陈长友.3mm倍频器MMIC的研究[D].石家庄:中国电子科技集团公司第十三研究所,2015.

Design of MMIC Quadrupler Based on Linear Superposition Technique

WANG Yabing，HE Qingguo，HU Zhifu

(Model Room，The 13th Research Institute of CETC，Shijiazhuang 050051, China)

Aiming at the problem of two stage frequency doubling cascade and large frequency conversion loss in the traditional passive quadrupler, a 40 GHz single stage passive MMIC quadrupler chip is developed by using linear superposition technique. The four-way phase shift power divider is designed by the cascade of planar ring balun and orthogonal hybrid network, which make the suppression of fundamental and other useless harmonics. The circuit design is simplified, and the frequency multiplication loss is reduced by this method. According to the simulation results, the tape-out and test for the quadrupler is completed. The measured results show that under the driving power of 20 dBm, the maximum output power is -2.7 dBm.

quadrupler; linear superposition; MMIC

2016- 03- 21

王亚冰(1990-)，男，硕士研究生。研究方向：器件建模和MMIC设计。

10.16180/j.cnki.issn1007-7820.2017.01.008

TN771

A

1007-7820(2017)01-026-03