功能梯度压电梁的非线性热电耦合分析
梁 校,郭传社,柳 明
(上海理工大学 机械工程学院,上海 200093)
功能梯度压电梁的非线性热电耦合分析
梁 校,郭传社,柳 明
(上海理工大学 机械工程学院,上海 200093)
针对功能梯度压电材料(FGPMs)压电单晶、双晶致动器在机械-电-热耦合下的静态弯曲、自由振动等问题。通过Timshenko梁理论和哈密顿方程推导出其控制方程,并考虑了横向剪切变形与轴向和旋转惯性效应。在此基础上,讨论了几何非线性对于压电悬臂梁的影响。数据表明,在模型趋于细长梁时(l/h≥30),梁的非线性项对于压电梁压电效应的影响误差最大可达到10%以上。
Timoshenko梁理论;功能梯度材料;制动器;几何非线性
压电材料由于具有良好的力电耦合特性而被广泛应用于诸多工程领域。为得到较大的驱动力,工程中目前使用的压电元件多为多层结构,如压电双晶片、Rainbow及压电堆等。这种结构,虽然获得了较大的驱动力,但元件中某些材料成分和性质的突然变化常常会导致结构中出现局部的应力失配,即在层间界面处存在明显的应力差,其后果就是粘结层在低温易开裂、高温易蠕变,进而缩短了元件的寿命。为解决这一缺陷,1995年,Zhu和Meng[1-2]将FGM的概念引入到压电材料中,成功制造出功能梯度压电驱动器。功能梯度压电材料就是将“压电材料”与“功能梯度材料”相结合发展起来的一种新型材料,兼具压电和梯度二者的优点,利用其制作压电元件可克服传统压电元件中服了纯压电材料在强度和脆性方面的缺陷。在压电材料分析的理论研究上,陈伟球等人[3]采用状态空间法,基于三维弹性理论,分析了横观各向同性压电板在四边简支条件下的自由振动问题。Roundy 等人[4]基于单自由度力学模型,研究了压电能量采集器的能量采集特性,并进行了相关实验验证。Sodano等人[5]利用 Hamilton 原理和 Rayleigh-Ritz 方法研究了单自由度压电梁模型,并进行了实验研究。Chen等人[6]根据Euler梁理论,获得了功能梯度压电梁的自由振动频率。Lee[7]采用有限元法分析了功能梯度双晶片在热电耦合作用下的位移与应力分布。假定压电梁由压电层、功能梯度压电层与弹性层3层组成,Joshi等人[8]讨论了温度对压电梁弯曲性能的影响。Adikary和Meng[9]对FGPM 驱动器的电阻特性进行了研究。Qiu和Tani等[10]对高性能功能梯度压电弯曲控制器的制备进行了研究。Chen和Ma[11]采用电泳沉积制备了功能梯度双晶压电控制器。Takagi和Li[12]对PZT/Pt FGPM 驱动器的自备和性能评估进行了实验并发现在电场作用下,观测到曲率呈弱非线性。本文从功能性压电致动器的控制方程出发、讨论了几何非线性对于压电制动器的影响。
1 Timoshenko梁的数学模型
考虑如图1所示的由NL层功能梯度材料组成的压电梁,其中,l,b,h分别为梁的长、宽和总厚度。建立如图1所示的直角坐标系x-o-z,压电梁受到分布载荷q(x,t)和电压V(t)的作用,且假设温度均匀变化量为ΔT。同时假设材料参数沿z轴均匀变化,并且与x轴无关。则第k层功能梯度压电梁的材料参数可表示为
(1)
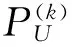
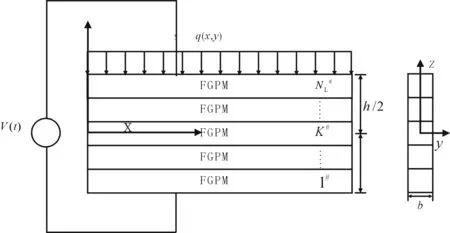
图1 功能梯度压电梁的模型图
根据Timoshenko梁理论[13],功能梯度压电梁的位移模式可给定为

(2)

Wang和Quek[14]给定了压电梁的电势满足

(3)
考虑几何非线性的影响,则Timoshenko梁的几何关系可表示为
(4)
其中,z方向位移w0表示初始的几何缺陷,同时忽略x方向初始缺陷的影响。
同时采用d型压电本构关系,采用平面应力假设,可得到功能梯度压电Timoshenko梁的本构关系为
(5)
其中,Q11,Q55为弹性刚度;α1是材料的热膨胀系数;p3为热电系数。同时由式(3)可得到Ex、Ez和E0,可分别表示为

(6)
采用Hamilton原理推导功能梯度压电梁的动力学控制方程,由总能量的变分可得
(7)
其中,电焓的变分δH,动能的变分δH及由外力q(x,t)所做功的变分δR可分别表示为
(8)
(9)
(10)
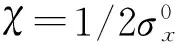
(11)
其中,公式中的系数满足

并由Timoshenko梁的物理意义可得到功能梯度压电Timoshenko梁的轴力N(x),剪力Q(x)和弯矩M(x)可表示为

(12)
(13)
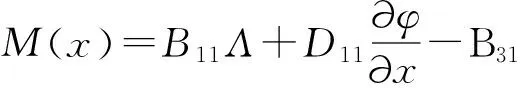
(14)
同时由相应的Hamilton原理可得到相应的电学边界条件为
(15)
给定初值条件为
(16)
因此,问题归结为求满足平衡微分方程方程式(11),力学边界条件和电学边界条件式(15)和初值条件式(16)的解。可见得到问题的解析解较为困难。文中采用微分求积法来对功能梯度压电层合梁结构进行求解。
2 数值结果
2.1 计算模型及参数
如图2所示,考虑几种功能梯度层合梁。其中每层梁厚为hk=Zk-Zk-1。功能梯度压电层(FGPM)选用PZT-4和PZT-5H作为两种基本组分,极化方向如图2所示。除了双晶体压材料的下层体分数按照式(17)取值外,其他各层按照式(18)取值。用λk表示第k层的梯度指标,为便于计算,假设每层的λk相同,并统一表示为λ
(17)
(18)

图2 不同的FGPM驱动器构型
本文引用各类材料的参数如下:
PVDF:E=2.0 GPa,G=0.8 GPa,V=0.29,d31=-23×10-12C/N,d15=-670×10-12C/N,∈11=12.43∈0,∈33=11.98∈0。
PZT-4:Q=81.3 GPa,Q55=25.6 GPa,d31=123×10-12C/N,d31=495×10-12C/N,∈11=1 470∈0,∈33=1 300∈0,p3=2.5×10-5C/(m2K),a1=0.2×10-5K-1,ρ=7 500 kg/m3。
PZT-5H:Q=60.6 GPa,Q55=23.0 GPa,d31=-274×10-12C/N,d31=741×10-12C/N,∈11=3 130∈0,∈33=3 400∈0,p3=0.548×10-5C/(m2K),a1=1×10-5K-1,ρ=7 500 kg/m3。
2.2 数值结果的验证
考虑标准压电双晶片(双层悬臂梁),由两层PZT-5H制作而成,两层的极化方向相反,上表面作用均布荷载q=10 kN/m2或外加电压为100 V,其自由端端部位移及基频列于表1中,解析解取自Lee等人的工作。当离散点数N=15时,本文数值方法趋于收敛,并与上述解析解吻合较好,验证了本文在静力荷载作用下及自由振动问题求解的准确性。

表1 在不同载荷下离散点的数量对数值求解的影响
采用有限元方法,Lee研究了功能梯度压电双晶片驱动器,尺寸为80 mm×10 mm×0.22 mm,即每层厚0.11 mm,外加电压为600 V,驱动器外表面为100%的PVDF,其挠度曲线如图3所示。本文结果与Lee的结果吻合良好。

图3 外加电压下(600V)的双晶FGPM变形曲线比较
2.3 非线性弯曲研究
(1)线性结果与非线性结果的比较。给定双晶压电梁的非均匀指标λ=1,6,载荷分别为:Q=60 KN,V=0 V和Q=0 KN,V=600 V。设长细比a=L/h。图4给出了在不同非均匀指标下, 对中点变形的影响。可以看出,无论是在给定力还是电载荷的情况下对于细长梁(l/h≥30)而言,几何非线性的影响会随着梁的增大而增大。由此可知在对细长的压电梁模型进行仿真与分析时,几何非线性的影响不可忽略。

图4 长细比对单晶梁中间点挠度的影响(λ=1,6)
(2)非均匀指标的影响。给定Q=60 kN,V=0 V和Q=0 kN,V=600 V,研究非均匀指标对双晶压电梁力学特性的影响(在机械载荷和电载荷作用下的非线性弯曲性能。计算中给定l/h=30。可看出在图5(a)施加力载荷中,长细比较小时非线性不明显,长细比增大非线性影响也慢慢明显,其影响最大值约为15%。在图5(b)施加电荷过程中,非线性影响一直存在,且大小随长细比变化不大,其值约为10%。

图5 非均匀指数对单晶的压电梁中点挠度的影响(l/h=30)
3 结束语
功能梯度压电制动器的机械—热—电耦合的研究主要依据Timoshenko梁理论和哈密顿原理,可得到压电制动器在考虑到横向剪切力等影响的控制方程,主要讨论了单晶体双晶体压电悬臂梁在不同长细比,不同非均匀指标下,施加不同载荷时线性结果与非线性结果的对比,可看出在不同情况下非线性对于压电梁的影响。计算发现在模型趋于细长梁时(l/h≥30),梁的非线性项对于压电梁压电效应有明显的影响。
[1] Zhu X H,Meng Z.A functionally gradient piezoelectric actuator prepared by powder metallurgical process in PNN-PZ-PT system[J].Journal of Materials Science Letters,1995, 14(5):16-18.
[2] Zhu X H,Meng Z.Operational principle,fabrication and displacement characteristics of a functionally gradient piezoelectric ceramic actuator[J].Sensors Actuators,1995,48(1):69-76.
[3] 陈伟球,边祖光,丁皓江.功能梯度矩形厚板的三维热弹性分析[J].力学季刊,2002,23(4):443-449.
[4] Roundy S,Wright P K.A piezoelectric vibration based generator for wireless electronics[J].Smart Material Structures,2004(13):1131-1142.
[5] Sodano H A,Park G,Inman D J. Estimation of electric charge output for piezoelectric energy harvesting[J].Strain,2004,40:49-58.
[6] Chen C D .On the singularities of the thermo-electro-elastic fields near the apex of a piezoelectric bonded wedge[J].Solids and Structures,2006,43(9):57-81.
[7] Lee H J.Layerwise laminate analysis of functionally graded piezoelectric bimorph beams[J].Journal of Intelligent Material Systems and Structures,2005,16(3):65-71.
[8] Joshi S, Mukherjee A,Schmauder S.Numerical characterization of functionally graded active materials under electrical and thermal fields[J].Smart Materials and Structures,2003,12(57):1-9.
[9] Adikary S U,Meng Z Y,Jin D R.A resistivity gradient piezoelectric FGM actuator[J].Journal of Materials Science & Technology,2000,16(38):3-6.
[10] Qiu J,Tani J,Ueno T,et al.Fabrication and high durability of functionally graded piezoelectric bending actuators[J].Smart Materials and Structures,2003,12(1):15-21.
[11] Chen Y H,Ma J,Li T.A functional gradient ceramic monomorph actuator fabricated using electrophoretic deposition[J].Ceramics International,2004,30(68):3-8.
[12] Takagi K,Li J F,Yokoyama S,et al. Fabrication and evaluation of PZT/Pt piezoelectric composites and functionally graded actuators[J].Journal of the European Ceramic Society,2003,23(15):77-83.
[13] Timoshenkosp.高等材料力学[M]. 胡人礼,译.北京:科学出版社,1979.
[14] Wang Q,Quek S T.Flexural vibration analysis of sandwich beam coupled with piezoelectric actuator[J]. Smart Materials and Structures,2000,9(10):3-9.
Thermo-electro-mechanical Nonlinear Characteristics of Functionally Graded Piezoelectric Actuators
LIANG Xiao,GUO Chuanshe,LIU Ming
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093, China)
Aiming at the static bending, free vibration, of monomorph, bimorph, and multimorph actuators made of functionally graded piezoelectric materials (FGPMs) under a combined thermal-electro-mechanical load. The governing equations of the beam are derived by using Timoshenko beam theory and Hamilton’s principle, and the transverse shear deformation and axial and rotational inertia effects are considered. On the basis of this, the influence of geometric nonlinearity on the piezoelectric cantilever beam is discussed. The data show that the effect which is caused by the nonlinear term of the beam may leading to error of 10% on the piezoelectric effect of the piezoelectric beam when the model tends to be a slender beam(l/h≥30).
Timoshenko beam theory; FGPMs; actuator; geometric nonlinearity
2016- 03- 15
上海市教委创新基金资助项目(12YZ092,12YZ074);沪江基金资助项目(D14005)
梁校(1990-),男,硕士研究生。研究方向:工程力学。
10.16180/j.cnki.issn1007-7820.2017.01.001
TN751.1
A
1007-7820(2017)01-001-05

