混凝土徐变对坝体温度应力场的影响
李钦智
(新疆石河子市新疆玛纳斯河流域管理局, 新疆 石河子 832000)
混凝土徐变对坝体温度应力场的影响
李钦智
(新疆石河子市新疆玛纳斯河流域管理局, 新疆 石河子 832000)
徐变对温度应力影响很大,可使其减小一半左右。本文用有限单元法研究徐变对大体积混凝土结构温度应力的影响,对混凝土结构温度应力进行仿真计算。结果表明,徐变度越大,温度应力越小,二者近似服从二次函数关系。徐变对温度应力场的影响受水管冷却措施的影响较大,当水管冷却时间较长或水化热发热速率较快时,徐变对温度应力的影响作用明显减小。
混凝土; 坝体; 徐变度; 温度应力; 水管冷却
1 引 言
由于施工时温度变化多样,大体积混凝土产生很大的拉应力,导致混凝土坝出现裂缝,直接影响工程施工安全。因此,对温度应力进行研究分析在混凝土结构设计中十分重要。在浇筑过程中,徐变对温度应力有很大影响。对大体积混凝土工程,徐变可降低或消除一部分由于温度变形所产生的破坏应力。徐变的计算模型有很多种,如:有效模量法模型及其改进模型[2],徐变固化理论模型及其改进模型[3-6],时间微分形式下的Maxwell模型、Kelvin模型和Burgers模型[7-9],老化理论模型,弹性徐变理论模型及弹性徐变老化理论模型等[1]。工程上一般建议采用朱伯芳提出的弹性徐变老化理论模型,它可以较好地反映早期混凝土在卸载作用下徐变的部分可恢复性质。此外,朱伯芳提出徐变对温度应力影响很大,可使温度应力减小一半左右[1]。在徐变对混凝土结构温度应力的影响方面,虽然分析研究不少,但考虑的因素不够全面,一些重要的因素没有考虑,如:水管冷却和水化热发热速率等,因此,有必要深入研究这些因素的影响。
本文根据弹性老化徐变理论式建立模型,对大体积混凝土进行描述;采用有限元法基本原理,编写C++程序TSC,对温度应力场进行仿真计算,从水管冷却、徐变和绝热温升3个条件入手,通过对混凝土浇筑块在有无水管冷却、有无徐变、不同绝热温升和不同冷却时长下进行温度应力计算分析,并对计算结果进行拟合。
2 基本理论
2.1 单元应力计算
在复杂应力状态下时,应力增量与应变增量的关系:
(1)

[B]——几何矩阵;
{Δδn}——位移增量矩阵;
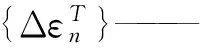
{ηn}——徐变应变。
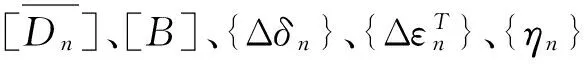
由温度场的有限元方程:
(2)
式中H——热传导矩阵;
R——热容矩阵;
Tn及Tn+1——n时刻和n+1时刻节点温度向量;
Fn+1——温度荷载向量。
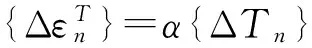
由徐变度公式:
(3)
其中
c1=0.23/E0;c2=0.52/E0
式中t——时间;
τ——加载龄期;
E0——混凝土弹性模量。
代入式(4)中:
(4)
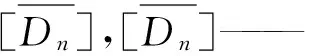
μ——泊松比;
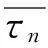
(5)
式中ψs、r0、r1——材料常数。
ηn可由递推公式算出,其中大部分变量为计算过程中的中间量,该递推式在运算中可将其抵消。
有限元的平衡方程为:
(6)
式中 [K]——结构刚度矩阵;
{Δδn}——位移增量矩阵;
{ΔPn}——外荷载增量;

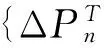

外荷载增量{ΔPn}=∭[B]T{Δσn}dv,其中{Δσn}为应力增量。
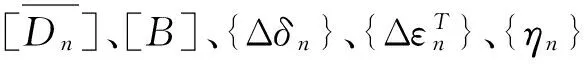
2.2 混凝土表面散热对水管冷却效果的影响
除了开始冷却时的混凝土温度To与水管水温Tω的差值(To-Tω)以及水泥水化热外,混凝土表面散热也会影响到水管冷却的效果。董福品提出了考虑混凝土表面散热对水管冷却效果影响的计算方法[10]。
把时间分为时段Δτi,Δτi=τi-τi-1,Tmi为第i时段末τi时刻混凝土的平均温度。假设Δτ由于混凝土表面散热引起的混凝土平均温度降低为ΔTu,且ΔTu只发生在时段末。
第n时段的ΔTun为:
(7)
混凝土外表面散热对水管冷却效果的影响计算如下:
(8)
式中Tfn——从τo到τn时间混凝土表面散热对水管冷却效果的影响。
3 计算模型及参数的选取
计算模型由混凝土浇筑块和基岩组成,浇筑块高13.5m,分9层浇筑,每层1.5m厚,假定每层瞬时浇筑完成,每个浇筑层划分为3层网格(见图1),混凝土浇筑层与层之间的浇筑间歇为10d。
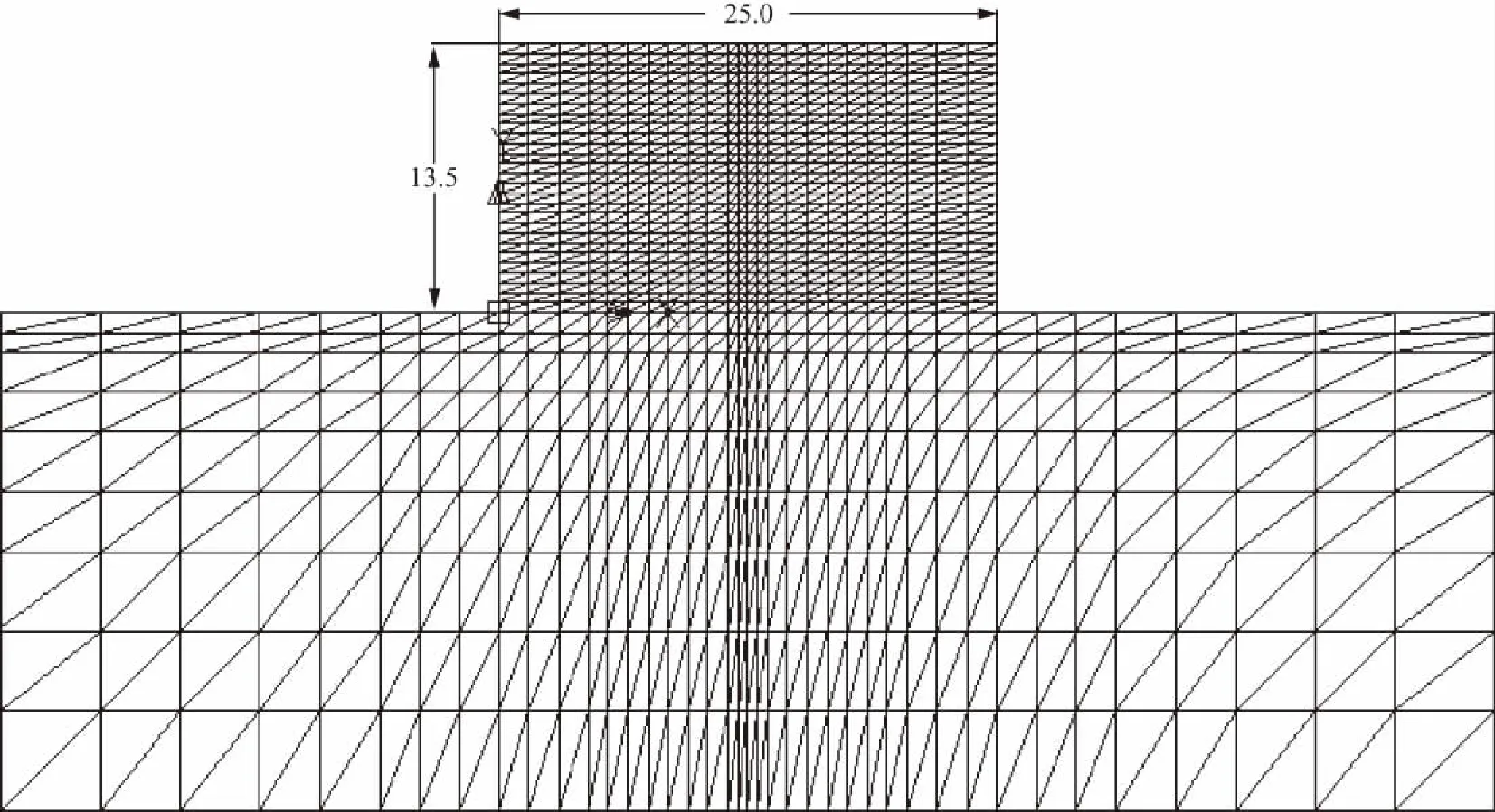
图1 计算模型
计算参数见表1。

表1 模拟参数
无水管冷却工况下,混凝土浇筑温度和气温均设为0℃。
有水管冷却工况下,设混凝土3月浇筑,浇筑温度取为17.1℃。表2为12个月的气温。

表2 气温
4 计算结果及分析
4.1 无水管冷却工况
由二结点法算出混凝土浇筑模型中间截面的最大主应力,对浇筑层的接触面运用线性插值法得出接触面上最大主应力,画出模型温度应力图。所得应力图见图2。(由于篇幅原因,且应力图走势相似,本文只以1倍徐变的应力图对其进行分析。)
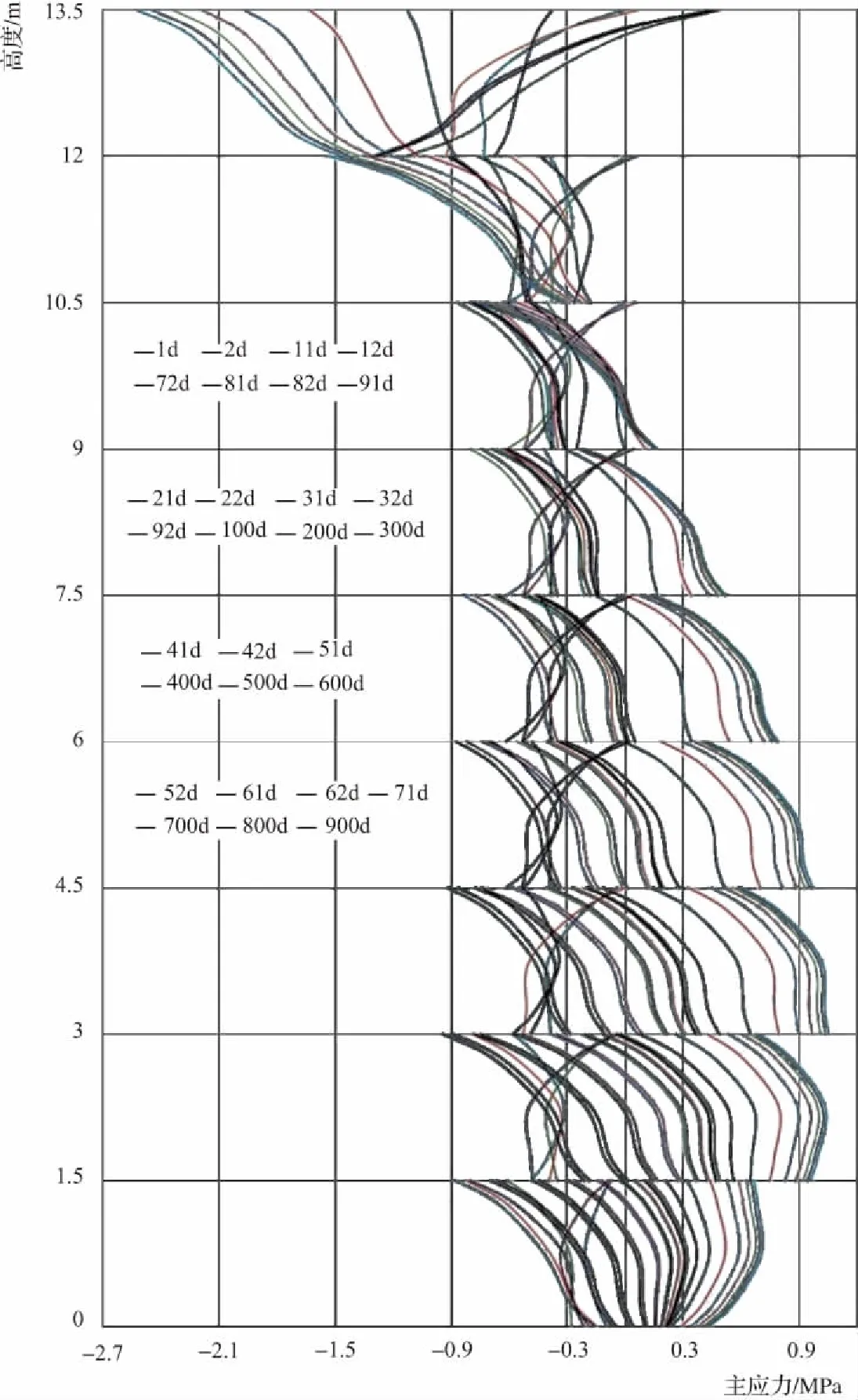
图2 模型中间截面应力图
由图2可知,浇筑初期,层面中间截面受到了压应力。因为暴露早期的混凝土表面温度升高,应力转为压应力。到后期混凝土表面完全冷却后,由于受到基础约束作用,压应力再转变为拉应力。由于前七层应力走势相似,现单独拿出最后两层详细说明。第九层浇筑于81d后,浇筑后表面长期暴露。早期部分受压,后期全面受压。由于长期暴露,表面温度降低,内部完全冷却后,表面产生了压应力。对于整体模型而言,上面两层可以近似看作模型的表面。所以第八层应力走势与第九层相似。而第八层较第九层更靠近内部,温度变化幅度不如第九层大,所以应力变化幅度不及第九层。
定义温度应力减小百分比为:
(9)
式中λ——温度应力减小百分比;
σ1——有徐变度时的最大主应力;
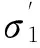
由模型计算结果可知:
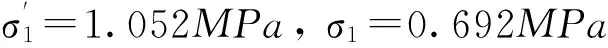
带入上式可得:
可以得出结论:混凝土的徐变对于温度应力具有很大影响。
考虑到不同徐变对温度应力会产生趋势效果,在计算中徐变度分别取为无徐变、0.8倍徐变、0.9倍徐变、1倍徐变、1.1倍徐变、1.2倍、1.3倍徐变,建立不同徐变度对温度应力的影响变化。计算结果见表3。

表3 无水管冷却的计算结果
根据表3,绘制徐变度的倍数c与λ、σ2的关系图,见图3。
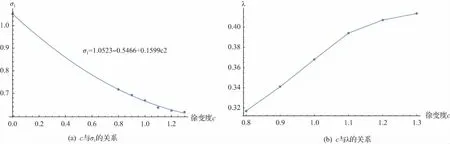
图3 c与λ、σ1的关系
由图3(a)可知,随着徐变增大,σ1逐渐减小,但其减小速率亦逐渐放缓,利用Mathematica对这组数据寻找最佳拟合函数为:
σ1=1.0523-0.5466c+0.1599c2; R2=0.99
(10)
由图3(b)可知,当徐变度在0.8~1.1时,λ随着徐变度的增大而增大,且其斜率固定,约为0.258;当徐变度在1.1~1.2时,其斜率约为0.13。说明当徐变度在1.1~1.2时,λ随着徐变度增大而增大的速率降低,约为前一段的50%。当徐变度在1.2~1.3时,其斜率约为0.075。说明当徐变度在1.2~1.3时,λ随着徐变度增大而增大的速率降低,约为前一段的50%;总体而言,λ随着徐变度的增大而增大。当徐变度小于1.1时,λ随着徐变度的增大以固定速率增长;当徐变度大于1.1时,λ的增长速率开始出现衰减,约为原来增长速率的50%。
4.2 有水管冷却工况
考虑在加入水管冷却条件下,徐变对混凝土温度应力的影响程度大小。水管采用HDPE管,外径32mm,长250m,水管水平间距2.0m,竖直方向间距1.5m,流量1.2m3/h,冷却水温为12℃。
在采用水管冷却措施工况下,分别计算不同水化热发热速率情况下有无徐变时的温度应力。计算中,混凝土的绝热温升θ=25τ/(n+)中n分别取值为1、2、4,水管冷却时间分别为15d和25d。计算结果见图4。
为了直观描述水管冷却和水化热发热速率对λ的影响绘制冷却15d时,水化热达到一半时龄期n与λ的关系,见图4(a);n=2时,冷却时间与λ的关系,见图4(b)。
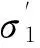
由图4(b)可知,在相同的水化热发展速率下,水管冷却间由15d增加到25d时,λ由47%降低为20%。可见,水管冷却时间对λ的影响很大。
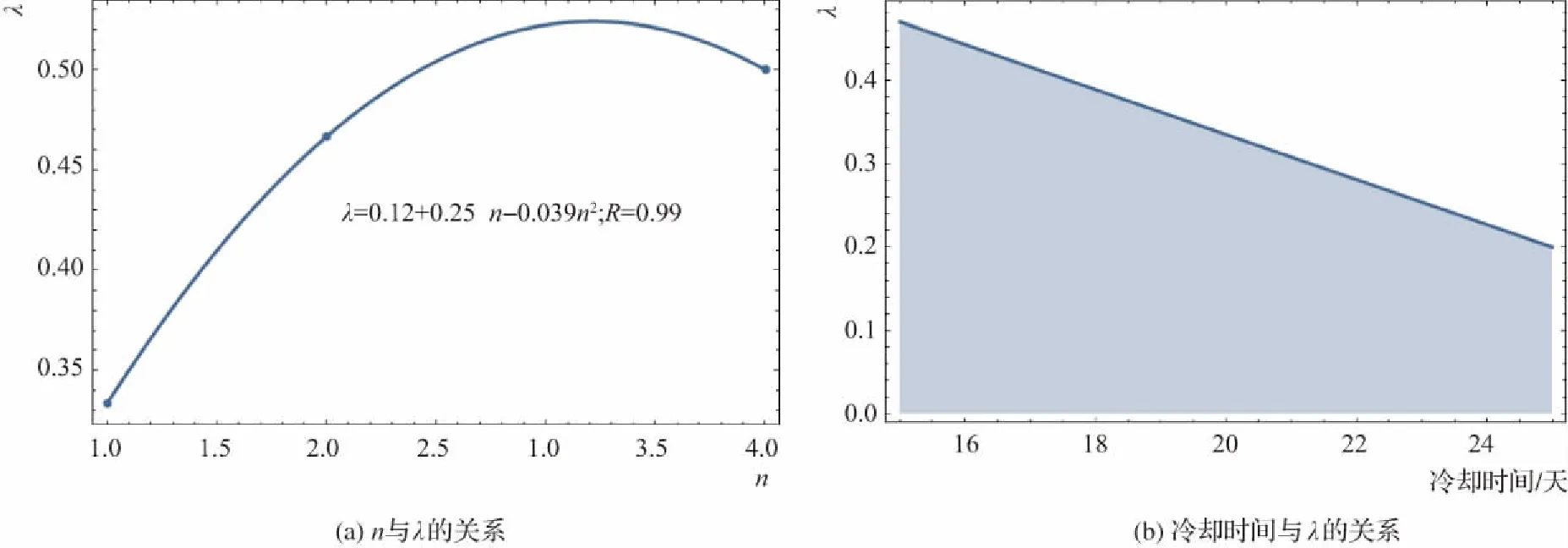
图4 冷却时间、n与λ的关系
5 结 论
a.随着混凝土徐变度的增大,大体积混凝土结构中的温度应力逐渐减小,但其减小速率亦逐渐放缓,温度应力和徐变度之间的函数关系近似为σ1=1.0523-0.5466c+0.1599c2。当徐变度小于1.1时,λ随着徐变度的增大以固定速率增长;当徐变度大于1.1时,λ增长速率开始出现衰减,约为原来增长速率的50%。
b.徐变对混凝土结构温度应力的作用受水管冷却的影响较大。在有水管冷却的工况下,随着水化热发展速率的增加,徐变对温度应力的影响作用先增大后减小。在相同的水化热发展速率下,当水管冷却时间增加时,徐变对温度应力的影响作用减小。
[1] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[2] Bazant Z P,Hon M,Mija H Hubler,et al.Improved estimation of long-term relaxation function from compliancefunction of aging concrete[J].Journal of Engineering Mechanics,2013,139(2):146-152.
[3] Bazant Z P,Prasannan S.Solidification theory for concretecreep(I) : formulation [J]. Journal of Engineering Mechanics,1989,115(8):1691-1703.
[4] Havlásek P,Jirásek M.Modeling of concrete creep basedonmicroprestress-solidification theory [J].Acta Polytechnica,2012,52(2):34-42.
[5] Wei Y,Hansen W.Tensile creep behavior of concretesubject to constant restraint at very early ages [J].Journalof Materials in Civil Engineering,2012,25(9):1277-1284.
[6] Wendner R,Hubler M H,Bazant Z P.The B4 model formulti-decade creep and shrinkage prediction [C].Proceedingsof CONCREEP-9.Cambridge:MIT,2013:429-436.
[7] Anders Boe Hauggaard,Lars Damkilde,Per Freiesleben Hansen.Transitional thermal creep of early age concrete[J].Journal of Engineering Mechanics,1999,125(4):458-465.
[8] 刘杏红,周伟,常晓林.改进的非线性徐变模型及其在混凝土坝施工期温度应力仿真分析中的应用[J].岩土力学,2009,30(2):440-446.
[9] 黄耀英,郑宏,周宜红.考虑混凝土龄期及弹塑性模型徐变的大体积混凝土温度应力研究[J].四川大学学报(工程科学版),2011,43(2):22-27.
[10] 董福品.考虑表面散热对冷却效果影响的混凝土结构水管冷却等效分析[J].水利水电技术,2001,32(6):16-19.
Influence of concrete creep on the stress field of dam temperature
LI Qinzhi
(XinjiangShiheziXinjiangManasRiverBasinAdministration,Shihezi832000,China)
Creep has high influence on temperature stress. It can be decreased by about 50%. In the paper, Finite element method is applied for studying the influence of creep on the temperature stress of mass concrete structure. The temperature stress of concrete structure is simulated and calculated. The results show that creep degree is larger, temperature stress is smaller, and they obey the quadratic function relation approximately. Creep influence on temperature stress field is influenced by water pipe cooling measures strongly. The influence and function of creep on temperature stress are reduced prominently when water pipe cooling time is longer or the heating rate of hydration heat is faster.
concrete; dam body; creep degree; temperature stress; water pipe cooling
10.16616/j.cnki.11- 4446/TV.2017.02.009
TV331
A
1005-4774(2017)02- 0029- 06

