基于网格无关性与时间独立性的数值模拟可靠性的验证方法

冯静安，唐小琦，王卫兵，应锐，张亭

（1石河子大学机械电气工程学院，新疆 石河子 832003；2华中科技大学机械科学与工程学院，湖北 武汉 430074）

基于网格无关性与时间独立性的数值模拟可靠性的验证方法

冯静安1,2，唐小琦2，王卫兵1*，应锐1，张亭1

（1石河子大学机械电气工程学院，新疆 石河子 832003；2华中科技大学机械科学与工程学院，湖北 武汉 430074）

数值模拟的可靠性验证是判断数值模拟可信度的重要方面。本文以水力旋流器一般研究中的纯水相仿真和多相流仿真为例，对数值模拟中的可靠性验证方法进行研究，探究Gambit下网格模型划分、网格质量检验方法、Fluent仿真方法、仿真中的边界条件设置方法、相关参数计算方法，并以此为基础对数值模拟可靠性验证中的网格无关性与时间独立性检验方法进行研究，分析了网格数量与时间步长对水力旋流器压力、速度、流量模拟结果的影响特性，探讨了网格数量与时间步长的确定方法。研究结果表明：以60 mm水力旋流器为例，网格数量不应低于15万；流量的计算较压力、速度的计算对时间步长具有更高的要求，一般精度要求下，计算压力、速度，时间步长不宜低于0.005 s，对于流量计算及压力、速度的高精度计算，时间步长不宜低于0.0001 s。

CFD；数值模拟；可靠性验证；网格质量；网格无关性；时间独立性；水力旋流器

随着计算机技术的发展，数值模拟方法的应用日趋广泛[1-4]。数值模拟能够求解理论分析无法求解的复杂流体力学方程，较实验方法的经济性好、适用性强，但数值模拟作为一种近似求解方法，其准确度受多方面因素影响，数值模拟的有效性还没有形成统一的判定标准[5-6]。针对特定工程问题选取适宜的数值模拟方法，采用仿真方法对数值模拟结果进行可靠性验证，再通过试验测试结果对数值模拟结果进行比对，依然是目前判断数值模拟结果可靠性的常规方法[7-8]。在对特定问题采取合理的数值模拟方法[9]时，数值模拟的准确度还受网格质量、网格数量、时间步长等因素影响[10-12]。至今，关于数值模拟可靠性验证方法的文献极少，模拟结果的可靠性大多仅依赖于最终的试验确认，而对所采用的网格模型质量、网格数量及时间步长未做出较全面的探讨。本研究针对上述存在的问题，以水力旋流器为对象，以水力旋流器一般研究中的纯水相仿真和多相流仿真为例，探究基于网格无关性与时间独立性的数值模拟可靠性验证方法，以供相关研究者借鉴和探讨。

1 模型与方法

1.1 Gambit网格模型及划分方法

1.1.1 Gambit网格模型

水力旋流器结构如图1所示，对应参数如表1所示。

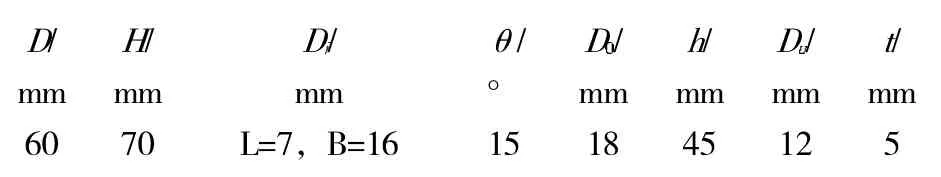
表1 水力旋流器结构参数Tab.1 Structural parameters of hydrocyclone

图1 水力旋流器结构图Fig.1 Structural diagram of hydrocyclone

网络模型的划分方法和网格质量对数值模拟结果具有极大影响[12]。采用合理的网格划分方法，尽可能对结构模型采用结构化网格划分，对减少网格数量、提高计算精度和计算效率具有重要作用。网格纵横比及偏斜度是判定网格质量的重要方面，应在网格划分后对其进行检查，尽量减小其数值大小。

在Gambit中建立水力旋流器网格模型。网格模型、网格纵横比及偏斜度的检验结果分别如图2所示。

网格划分方法。主要是依据表1中的水力旋流器结构参数，将旋流器划分为四部分，分别为入口及入口下表面到柱段上表面部分、入口下表面到柱段下表面部分、溢流管、锥段，全部采用cooper方式生成六面体网格。

图2 水力旋流器网格模型Fig.2 Grid model of hydrocyclone

1.2 Fluent仿真模型

1.2.1 数值模拟方法

湍流模型选取雷诺应力模型，近壁面处理采用标准壁面函数；多相流模拟采用Mixture模型；求解器采用压力基求解器、非稳态时间格式；求解方法采用SIMPLEC压力-速度耦合算法，压力插值格式应采用PRESTO!格式，动量、湍动能、湍流耗散率选择二阶迎风格式，多相流模拟时的体积分数选择QUICK插值格式。

1.2.2 边界条件设置

（1）入口采用速度入口方式，速度方向为边界的法相，入口速度νi=5 m/s；

（2）溢流口和底流口均采用压力出口，采用相对压力，压力值为0，即出口直接与大气相连通，其余均为默认值；

（3）壁面均采用非滑移边界条件，即壁面速度为0；（4）入口处的湍流定义方法采用湍流强度和水力直径；（5）溢流口与底流口的湍流定义方法采用“K and Epsilon”方式，并取默认值；

（6）纯水仿真与多相流仿真中的有关参数根据相关公式计算得到，其中多相流仿真采用混合固相，其质量浓度为CW=0.20，粒度为20 μm；混合固相中的2种固相质量分数分别为：ω1=0.85，ω2=0.15；密度分别为ρ1=2.234 t/m3；ρ2=3.2 t/m3。

1.2.3 相关参数计算方法

相关参数计算公式如下：

式(1)-(9)中：ρ 为固相混合密度,t/m3；φ1、φ2为固相体积分数；ρm为矿浆密度，t/m3；I为湍流强度；dH为水力直径，mm；Re为雷诺数；μm为矿浆粘度，kg/ms；CW为质量浓度；CV为体积浓度。

2 数值模拟的可靠性验证及分析

2.1 纯水相仿真的可靠性验证及分析

对于非稳态数值模拟，需要确定所用网格的数量、时间步长以及与计算结果之间的无关联性，即要对网格进行无关联性验证和时间独立性（无关性）验证。本文主要探讨模拟计算结果中的压力、速度、流量等的无关性检验。

2.2 网格无关性检验

按时间步长0.001 s，对A、B、C、D四种网格数量进行无关性检验，采用纯水相模拟，通过仿真模拟达到稳态后，得出的结果如表2所示。

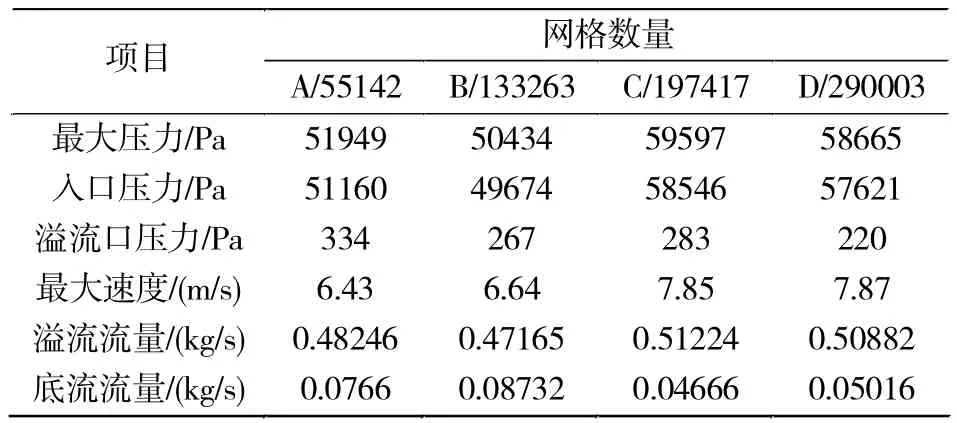
表2 纯水相仿真的网格无关性检验结果Tab.2 Pure water simulation results of the grid independence verification

由表2可知：网格数量对仿真模拟结果具有极大影响，网格数量低于15万时，各检测项目均与高网格数量计算值存在较大差异，而当网格数量超过约20万时，模拟结果变化差异不大。

进一步分析不同网格数量下压力和速度的分布情况。通常认为旋流腔主要作用是对流体预旋、稳定流场，而锥段起主要分离作用，因此，本文对旋流腔与锥段结合面所在高度对流场压力分布及速度分布进行分析，结果如图3所示。

图3 柱锥结合面处的压力分布（a）与速度分布（b）Fig.3 Pressure distribution(a)and velocity distribution(b)of columns taper binding surface

由图3可以看出：网格数量对压力分布和速度分布具有较大影响；在网格数量超过约20万时，模拟结果十分接近，即网格数量增大到一定程度后计算结果趋于稳定。综合考虑计算时间与仿真误差，可以近似认为网格数量C可满足网格数量的无关性要求。

2.2 时间独立性检验

以网格数量C为网格模型，按时间步长0.005、0.001、0.0001 s，对所选网格数量进行时间独立性检验。在模拟进行到稳态后，得出的计算结果如表3所示。

由表3可知：在网格数量达到一定程度后，时间步长对压力、速度的模拟结果差异不大，但时间步长对流量的模拟结果影响较大；相比压力的计算，在进行流量计算时应选取更小的时间步长。

表3 纯水仿真的时间独立性检验结果Tab.3 Pure water simulation results of the time independence verification

进一步对不同时间步长下的压力分布和速度分布进行分析。同样选取旋流腔与锥段结合面所在高度对流场压力分布及速度分布进行分析，结果如图4所示。

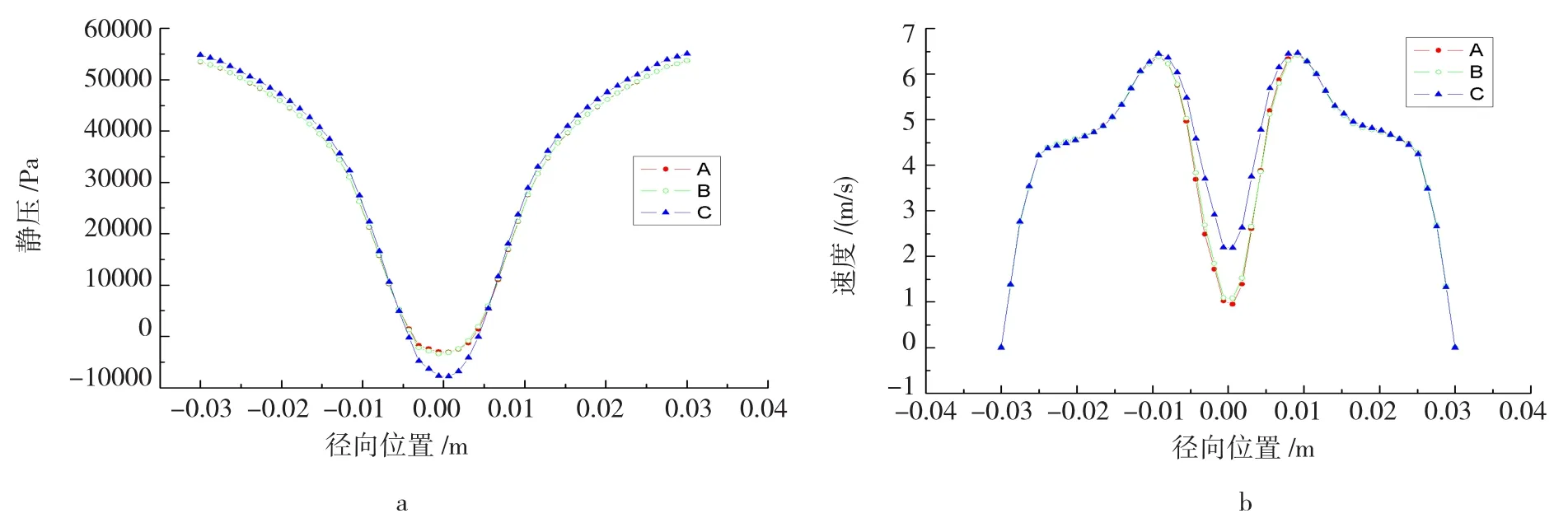
图4 柱锥结合面处的压力分布（a）与速度分布（b）Fig.4 Pressure distribution(a)and velocity distribution(b)of columns taper binding surface

由图4可知：时间步长对压力分布和速度分布的计算结果具有一定影响；在半自由涡区域，时间步长对计算结果的影响不大，但在强制涡区域，时间步长对压力分布和速度分布的计算结果差异均较大。综合考虑，选取0.0001 s的时间步长更为适宜。

3 混合相仿真的可靠性验证与分析

以网格数量C为网格模型，对混合相进行仿真数值模拟的可靠性验证分析。按时间步长 0.005、0.001、0.0001 s，对所选网格数量进行时间独立性检验。在仿真模拟进行到稳态后，得出的结果如表4所示。

由表4可知：在网格数量达到一定程度后，时间步长对压力、速度的模拟结果差异不大，但对溢流、底流流量的影响较大。时间步长较大时，流量的模拟结果差异较大；当时间步长达到0.001 s时，流量的模拟结果较为接近，特别是对固相流量的模拟结果较为接近，但矿浆总体流量与水相流量的偏差较大。

表4 混合相仿真的时间独立性检验结果Tab.4 Multiphase simulation results of the time independence verification

进一步对不同时间步长下的压力分布和速度分布进行分析。选取旋流腔与锥段结合面所在高度对流场压力分布及速度分布进行分析，结果如图5所示。

由图5可以看出：时间步长对压力分布和速度分布在半自由涡区域的影响不大，但对强制涡区域存在一定影响，相比0.0001 s时间步长，时间步长较大时，强制涡域的压力计算结果偏大，而速度的计算结果偏小。综合考虑时间步长对各类误差的影响，同时结合时间步长对仿真计算时间的影响，选取0.0001 s的时间步长更为适宜。

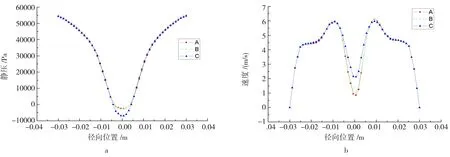
图5 柱锥结合面处的压力分布（a）与速度分布（b）Fig.5 Pressure distribution(a)and velocity distribution(b)of columns taper binding surface

4 结论

（1）提高数值模拟结果的可信度，应针对研究对象采取合理的网格划分方法，建立高质量的网格模型，依据研究对象确定合理的数值模拟方法，在此基础上，进行网格无关性与时间独立性检验，综合考虑计算精度和计算效率，选取合理的网格数量和时间步长。

（2）为减少仿真时间，多相流仿真时，宜先对单一相进行网格无关性检验，确定合理的网格数量，进而对多相流做时间独立性检验。

（3）相比于压力、速度的计算，时间步长对流量计算的影响更大，因此，在流量计算时应选取相对压力、速度计算更小的时间步长。

[1]Bhaskar K U，Murthy Y R，Raju M R，et al.CFD simulation and experimental validation studies on hydrocyclone[J].Miner Eng 2007，20:60-71.

[2]Gao S，Wei D，Liu W，et al.CFD numerical simulation of flow velocity characteristics of hydrocyclone[J].T Nonferr Metal Soc，2011，21:2783-2789.

[3]Swain S，Mohanty S.A 3-dimensional Eulerian-Eulerian CFD simulation of a hydrocyclone[J].Appl Math Model，2013，37:2921-2932.

[4]Safa R，Soltani Goharrizi A.CFD simulation of an industrial hydrocyclone with Eulerian-Eulerian approach:A case study[J].International Journal of Mining Science and Technology，2014，24:643-648.

[5]Stern F，Wilson R，Coleman H W，et al.Comprehensive approach to verification and validation of CFD simulations-Part 1:Methodologies and procedures[J].Journal of Fluids Engineering Transactions of the ASME，2001，123:793-802.

[6]张涵信，查俊.关于CFD验证确认中的不确定度和真值估算[J].空气动力学学报，2010，28(1):39-45. Zhang H X，Zha J.The uncertainty and truthvalue assessment in the verification and validation of CFD[J].Acta mechanica sinica，2010，28(1):39-45.

[7]白文.计算流体力学模拟可信度分析的基本术语[C]//中国空气动力学会.中国航空学会，等.计算流体力学研究进展——第十一届全国计算流体力学会议论文集，2002: 410-415.

[8]张涵信.关于CFD计算结果的不确定度问题[J].空气动力学学报，2008，26(1):47-49，90. Zhang H X.On the uncertainty about CFD results[J].Acta Aerodynamica Sinica，2008，26(1):47-49，90.

[9]梁政，吴世辉，任连城.论水力旋流器流场数值模拟中湍流模型的选择[J].天然气工业，2007(3):119-121. Liang Z，Wu S H，REN Lian cheng.The selection of turbulent model in numerical simulation of flow field of hydraulic cyclone[J].Natural Gas Industry，2007(3):119-121.

[10]侯中喜，夏刚，王承尧.CFD解的数值可靠性分析[C]//中国空气动力学会，等.计算流体力学研究进展——第十二届全国计算流体力学会议论文集，2004:790-795.

[11]康顺，石磊，戴丽萍，等.CFD模拟的误差分析及网格收敛性研究[J].工程热物理学报，2010，31(12):2009-2013. Kang S，Shi L，Dai L P，et al.Analyse of CFD Simulation Error and Study of Grid Convergence[J].Journal of Engineering Thermophysics，2010，31(12):2009-2013.

[12]李涛，左正兴，廖日东.结构仿真高精度有限元网格划分方法[J].机械工程学报，2009，45(6):304-308. Li T，Zuo Z X，Liao R D.Meshing Method of High Precision FEM in Structural Simulations[J].Chinese Journal of Mechanical Engineering，2009，45(6):304-308.

Reliability verification method of numerical simulation based on grid independence and time independence

Feng Jingan1,2,Tang Xiaoqi2,Wang Weibing1*,Yingrui1,Zhang Ting1
(1 College of Mechanical and Electrical Engineering,Shihezi University,Shihezi,Xinjiang 832003,China; 2 School of Mechanical Science and Engineering,Huazhong University of Science and Technology,Wuhan，Hubei 430074,China)

The reliability verification of numerical simulation is an important aspect to judge the credibility of numerical simulation.In this paper,pure water phase simulation and multiphase flow simulation in hydrocyclone research are taken as an example to study the method of reliability verification in numerical simulation.The grid model partitioning and grid quality testing method under Gambit,Fluent simulation method,boundary condition setting method and therelevant parameter calculation method in the simulation are discussed in detail.Based on this,the method of grid independence and time independence verification in the numerical simulation reliability verification are studied,and the number of grids and time step on the pressure,velocity and flow simulation results of hydrocyclone,the method of determining grid number and time step are discussed.The results are shown as follows:as the example of 60 mm hydrocyclone,the number of grids should not be less than 150000;the calculation of flow rate has higher requirements on time step than the calculation of pressure and velocity. The calculation of pressure and velocity in general accuracy,The time step should not be less than 0.005 s,and the time step should not be less than 0.0001 s for the calculation of flow rate and the calculation of pressure and velocity.

CFD;numerical simulation;reliability validation;grid quality;grid independence;time independence;hydrocyclone

TB24;TD455.5

A

10.13880/j.cnki.65-1174/n.2017.01.009

1007-7383(2017)01-0052-05

2016-10-11

国家自然科学基金项目（51264034），石河子大学应用基础研究青年项目（2015ZRKXYQ04）

冯静安（1977-），男，副教授，从事计算流体力学研究，e-mail：fja_mac@shzu.edu.cn。

*通信作者：王卫兵（1967-），男，教授，从事机械制造装备研究，e-mail：wwb_mac@shzu.edu.cn。