坐标解析形合数 图形分离繁化简——2016年中考“图形与坐标”专题解题评析

叶茂恒

（浙江省温州市第十七中学）

坐标解析形合数 图形分离繁化简
——2016年中考“图形与坐标”专题解题评析

叶茂恒

（浙江省温州市第十七中学）

通过对2016年全国各地100多份中考试题的扫描，针对其中有关图形与坐标试题进行整理与解析.其中考点分析部分，针对不同考点，通过典型试题进行考点分析和解法点拨；典型解法评析，阐述了典型解法的产生思路、解法特色，对典型试题进行了归类与分析；最后列举试题的部分新颖解法，以期抛砖引玉.

数学中考；图形与坐标；图形的位置；数形结合

《义务教育数学课程标准（2011年版）》（以下简称《标准》）将“几何与图形”分成图形的性质、图形的变化、图形与坐标三大块，其中图形与坐标主要内容包括坐标与图形位置、坐标与图形运动（含轴对称、平移、旋转、位似等），不难发现图形与坐标是在图形的性质与图形的变化的基础上用坐标结合图形的性质研究图形的位置与变化，从代数角度研究几何图形，通过数与形相结合，从定量与变量等角度研究几何图形.2016年中考试卷图形与坐标试题分布较广，涵盖易、中、难各个层次，在各地的中考试卷中都占有重要的地位.尤其在压轴题上，可以发现图形与坐标是很多中考压轴题的主要背景：一方面，由于压轴题中的几何图形覆盖面广、综合性强、思维含量大，本身就是难点；另一方面，几何问题放置在坐标系中综合了代数问题，使得问题更为复杂，往往是学生解题的困难所在.而这些难点的突破，要有扎实的双基，要有丰富的解题经验，要善于将动态问题分类成多个静态问题，要善于从复杂图形中分离出基本图形，结合基本结论求解，还要善于将代数与几何相结合，灵活运用几何法或解析法分析问题、解决问题.

一、主要考点分析

图形与坐标是初中数学的主干知识，在中考卷中分布较广，涉及的知识点不仅多而且重要，常与几何图形、函数、方程等知识结合，考查的方式有选择题、填空题、解答题等，考查形式灵活多样，2016年中考试题也不例外.

（一）坐标与图形位置

1.考查点坐标的确定

例1（福建·福州卷）如图1，以点O为圆心，半径为1的弧交坐标轴于A，B两点，P是上一点（不与点A，B重合），连接OP，设∠POB=α，则点P的坐标是（ ）.

（A）（sinα，sinα） （B）（cosα，cosα）

（C）（cosα，sinα） （D）（sinα，cosα）

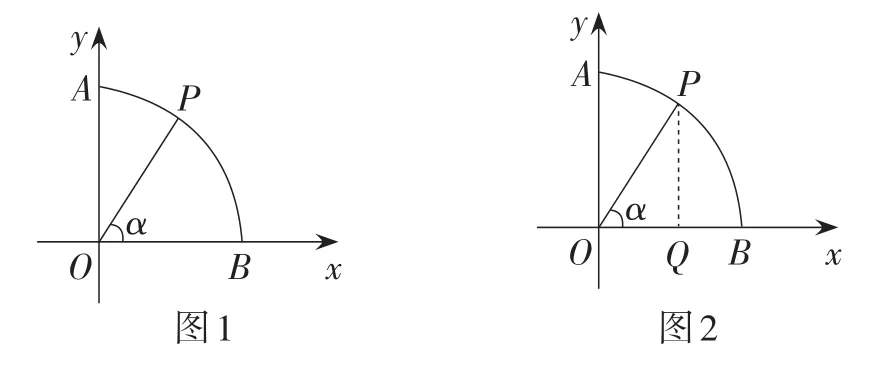
【解法点拨】此题以圆弧上的动点为背景构造了一个由方向和距离确定的点，求解该点在平面直角坐标系中的坐标，试题将两个定位法巧妙结合在一起，并考查两种定位法的表示法的相互转换，独具匠心.一方面，由于要确定点的坐标，要过点作坐标轴的垂线段；另一方面，由于要应用三角函数，也要构造直角三角形.因此，如图2所示构造Rt△POQ得点P的坐标为P（cosα，sinα），故选C.可见，此类问题难度不大，要确定点的坐标，关键在于构造含所求点的直角三角形，解直角三角形即可确定坐标.

2.考查已知坐标确定点的位置

例2（内蒙古·赤峰卷）如图3，在平面直角坐标系内按下列要求完成作图（不要求写作法，保留作图痕迹）．

（1）以（0，0）为圆心，3为半径画圆；

（2）以（0，-1）为圆心，1为半径向下画半圆；

（3）分别以（-1，1），（1，1）为圆心，0.5为半径画圆；

（4）分别以（-1，1），（1，1）为圆心，1为半径向上画半圆．

注：向上、向下指在经过圆心的水平线的上方和下方.

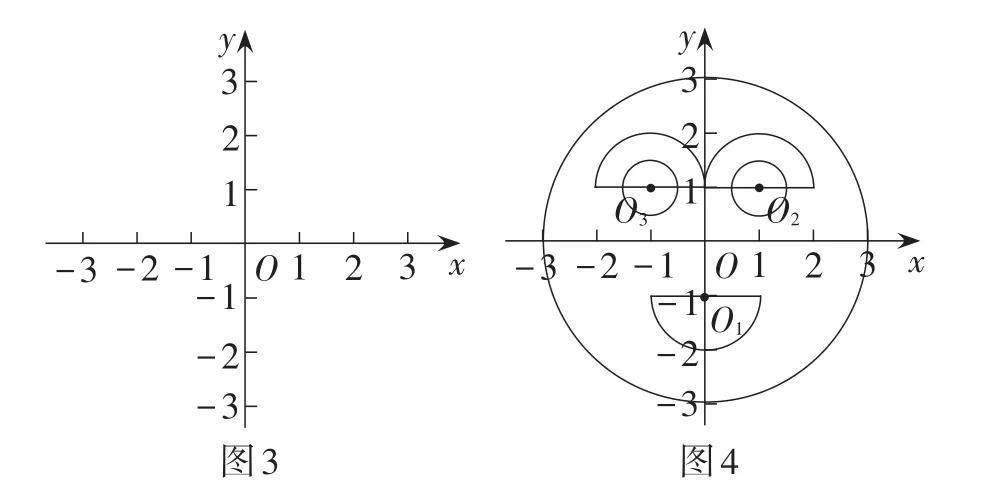
【解法点拨】此题为作图题，考查在平面直角坐标系中按一定要求作圆，由圆心确定位置，半径确定大小.试题中以坐标定位圆心位置，分别以4道小题作圆或半圆，着重考查坐标系中点坐标的确定，及坐标系如何借助坐标取定长线段，解答如图4所示.此题表面上看起来是作圆的作图题，但本质上是坐标点的确定，坐标内两点间距离的获取，及坐标系中坐标轴的方向的确定.

3.考查点坐标象限特征

例3（吉林·长春卷）点P（x-2，x+3）在第一象限，则x的取值范围是___________．

【解法点拨】此题将坐标系中各象限中的点的横、纵坐标的符号特征结合不等式考查，由第一象限中点的横、纵坐标都为正，列出不等式组即可求解.由于点P（x-2，x+3）在第一象限，所以解得x＞2.此类试题在各地、市卷中常有出现，考法的变化不大，难度也较低，属于基础题，问题的解决关键在于象限点坐标特征的掌握与不等式组的求解.

4.考查两点间距离问题

例4（山东·潍坊卷）如图5，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ）.

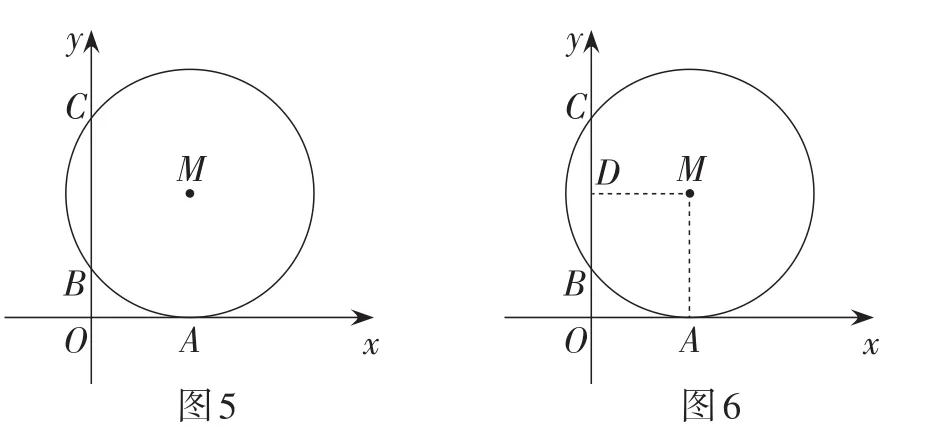
【解法点拨】此题考查平面直角坐标系中点到原点的距离，问题的解决涉及垂径定理与勾股定理的应用.因为⊙M与x轴相切于点A（8，0），故连接MA，可得MA⊥OA.可知点M与点A的横坐标相同为8.只需求得纵坐标即可求解点M与点O的距离.又因为BC为⊙M的弦，不妨作MD⊥BC于点D（如图6），由垂径定理得D为BC的中点.故点D的坐标为D（0，10）.所以MA= OD=10，即点M的坐标为M（8，10）.在Rt△OMA中，有.故选D．此题辅助线添加的思考基础有四点：一是在平面直角坐标系中，求两点间距离，需要点的坐标，一般要构造坐标轴的垂线段来求；二是初中阶段两点间距离公式教材没有要求，所以求两点间距离通常构造直角三角形，结合勾股定理求；三是圆中有弦，常作表示弦心距长度的垂线段结合垂径定理可将半弦、半径、弦心距三者联系起来；四是圆的切线问题，连半径得垂直是常用方法.基于这四点线索，辅助线一半径、一弦心距呼之欲出，这也是这四类相关问题常用的辅助线的作法，教学中值得关注.当然，对于在平面直角坐标系中有更多拓展研究的学生来说，中点公式加上两点间距离公式即可得解.

5.考查中点坐标问题

例5（山东·淄博卷）如图7，抛物线y=ax2+ 2ax+1与x轴仅有一个公共点A，经过点A的直线交该抛物线于点B，交y轴于点C，且点C是线段AB的中点.

（1）求这条抛物线对应的函数解析式；

（2）求直线AB对应的函数解析式．

图7

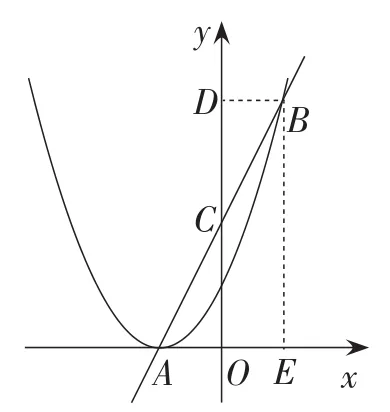
图8

【解法点拨】此题主要考查求一次函数的解析式和二次函数的解析式，但在求解析式时需要先确定抛物线和直线上的点.点A的坐标可根据抛物线与x轴只有一个公共点得Δ=4a2-4a=0.解得a=1.再求得A（-1，0）.也可由抛物线的顶点横坐标为，得点A的坐标为A（-1，0）.进而由顶点纵坐标为0，得a-2a+ 1=-a+1=0.得a=1.故抛物线解析式为y=x2+2x+1.对于点B的求解，可先求横坐标，再结合抛物线解析式求纵坐标.由于初中线段中点坐标公式没有要求，可以考虑用几何法求解.由于C为AB中点，常用辅助线构造全等三角形或是构造中位线，在平面直角坐标系中也不例外，因此可过点B作BD⊥Oy于点D，构造△BCD≌△ACO，或是过点B作BE⊥Ox于点E（如图8），此时OC为△ABE的中位线（即O为AE中点），易得点B的横坐标为1，代入抛物线解析式得点B的坐标为B（1，4），所以直线AB的解析式为y=2x+2.从问题的解决过程可以发现，在平面直角坐标系中涉及中点的问题可构造全等三角形或中位线求解，若有等腰三角形可结合三线合一，若在直角三角形中也可结合直角三角形斜边上的中线性质，若有圆与弦也可用垂径定理.在平面直角坐标系中，几何问题的解决既要联系图形的坐标，又要联系几何图形的原有性质及常用辅助线的添加方法，依托坐标轴构造常用基本图形.

6.考查方向距离定位法

例6（黑龙江·哈尔滨卷）如图9，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的点A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的点B处，则此时轮船所在位置B处与灯塔P之间的距离为（ ）.

（A）60海里

（B）45海里

图9

【解法点拨】此题考查平面内两点之间的距离，但点的位置不是用平面直角坐标定位法，而是用方向距离定位法，通过轮船的行驶过程给出点A，B的方向角及点A，P之间的距离.要求P，B两点之间的距离可以将有关角与边长转化到△ABP中，原问题等价为：在△ABP中，∠A=60°，∠B= 30°，PA=30海里，求PB的长.由于∠A与∠B互余，即△ABP是直角三角形，这是一个已知锐角与一边求解直角三角形的基础问题，结合三角函数即可求得BP=（海里）.故选D.此题提供的两个方向角关系较为特殊，恰为互余，△ABP恰为直角三角形.若△ABP不是直角三角形，如∠A=60°，∠B=45°，可考虑作出三角形的高将△ABP分为两个特殊直角三角形求解即可，这是已知两角一边或两边一角的三角形求解基本方法.总之，此类方向距离定位法问题通常要将这些方向角与距离放置在直角三角形中，结合三角函数或勾股定理求解.

（二）坐标与图形运动

1.考查坐标平面内图形的轴对称与平移变换

例7（甘肃·白银卷）如图10，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．

（1）画出△ABC关于x轴的对称图形△A1B1C1；

（2）将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．

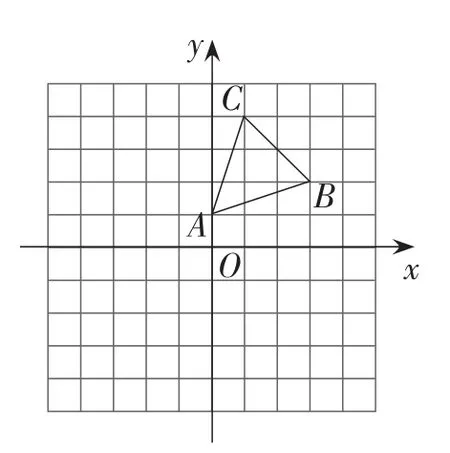
图10

图11

【解法点拨】第（1）（2）小题分别考查平面直角坐标系中图形的轴对称作图与图形平移运动点的坐标确定.由于知道△ABC的三个顶点的坐标，要画出△ABC关于x轴的对称图形可先确定三个顶点关于x轴的对称点坐标，根据关于x轴对称坐标变化规律“纵变横不变”可得△A1B1C1的三个顶点坐标分别为A1（0，-1），B1（3，-2），C1（1，-4），将这三点描出并连线即可画出△A1B1C1（如图11），此作图也可以利用对称点被对称轴垂直平分这一性质来完成.第（2）小题是平移运动，可以画图求得，或是利用点平移坐标变化规律“左减右加，上加下减”得A2（-3，-1），B2（0，-2），C2（-2，-4）．在平面直角坐标系中的轴对称与平移运动后点坐标的确定可以借助网格线画图，也可以利用坐标变化规律直接得到，为避免大意失分，有条件时可以两种方法互参为证.

2.考查坐标在直角平面内图形的中心对称与旋转变换

例8（湖北·武汉卷）已知点A（a，1）与点A′（5，b）关于坐标原点对称，则实数a，b的值是（ ）.

（A）a＝5，b＝1 （B）a＝-5，b＝1

（C）a＝5，b＝-1 （D）a＝-5，b＝-1

【解法点拨】关于原点对称的对称点坐标性质是坐标平面中心对称常见考查方式，此题中由于点A（a，1）与点A′（5，b）关于坐标原点对称，所以a与5，1与b互为相反数，故a＝-5，b＝-1，选D.此类问题，通常以原点为对称中心来命题考查，若问题中的图形不是关于原点中心对称，则可以应用中心对称中对称点连线被对称中心平分这一性质解决，如点A（a，b），B（c，d）关于点C（e，f）中心对称，由于对称中心C为对称点A，B连线的中点，则有，还可以结合中点有关性质求坐标，如转化为平移、中位线或全等图形等问题来解决.

3.考查平面直角坐标系内图形的位似变换

例9（黑龙江·齐齐哈尔卷）如图12，在平面直角坐标系中，矩形AOCB的两边OA，OC分别在x轴和y轴上，且OA= 2，OC=1.在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2，…，依此类推，得到的矩形AnOCnBn的对角线交点的坐标为_______．

图12

【解法点拨】此题考查平面直角坐标系中位似中心为坐标原点的图形的位似变换，问题解决的关键是掌握位似中心为原点的位似变换的基本性质.如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k.由已知条件得点B的坐标为B（-2，1），结合位似比为，所以点B1的坐标为.类似地，点B2的坐标为… 所以有点Bn的坐标为又由矩形对角线交点为对角线的中点，可表示为化简得.此题也是一道规律题，在平面直角坐标系中关于坐标的规律题一般由一种或两种变换连续变化而得，采用位似变换的构造规律的题不是很多，这类题通常以平移或旋转为主，这种问题的解决一般要根据相应的变换性质确定三个以上的点的坐标，这里的坐标可能有时需要保留算式，在算式中可能存在较为直观的规律，有时可能需要计算结果，根据结果数来研究规律，要灵活处理，这也是对数感的考查.

（三）综合应用

1.考查点坐标规律

例10（山东·德州卷）如图13，在平面直角坐标系中，函数y=2x和y=-x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l1于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l1于点A3，过点A3作y轴的垂线交l2于点A4，…，依次进行下去，则点A2017的坐标为_________．

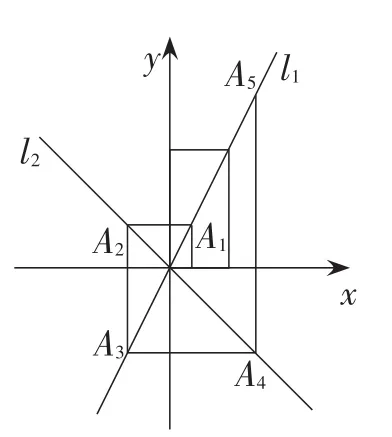
图13

【解法点拨】此题考查坐标点的规律寻找，注意到这些点分别分布在四个象限，通常要分类讨论，其分类的标准是An中的n除4的余数决定的.若k为自然数，当n=4k+1时，点An在第一象限；当n=4k+2时，点An在第二象限；当n=4k+3时，点An在第三象限；当n=4k时，点An在第四象限.因为2017=4×504+1，所以点A2017在第一象限.观察第一象限点A1（1，2），A5（4，8），A9（16，32），…，可知A4k+1（22k，22k+1）.所以A2017的坐标为A2017（22×504，22×504+1）=（21008，21009）.故答案为（21008，21009）．此题还可以以点在不同的直线上为标准分为两类求解，在平面直角坐标系中点的规律问题先要考虑要不要分类，分类的依据如何，再考查坐标的规律.实质上，这类问题一般有两个规律要找：一是要找点的脚码与点分布位置的规律，此时可以结合图形的象限或坐标轴分布情况分类，还可以多画一些图形，以提高直观辨识能力；二是找在脚码分类后的点坐标自身的规律，要注意观察上一个点与下一个点坐标之间的联系，可能会存在等差或等比关系.

2.考查综合问题中几何图形的顶点坐标的确定

例11（内蒙古·呼和浩特卷）已知▱ABCD的顶点A在第三象限，对角线AC的中点在坐标原点，一边AB与x轴平行且AB=2，若点A的坐标为A（a，b），则点D的坐标为_________．

【解法点拨】此题考查的是平面直角坐标系中平行四边形的顶点坐标的确定，由已知条件可知原点为平行四边形的对称中心，因此点B与点D也关于原点中心对称，要求点D的坐标，可先求点B的坐标.由“一边AB与x轴平行且AB=2”知点A，B之间的水平距离为2，问题等价于将点A向左或向右平移2个单位，求点B的坐标，但由于没有说明平移方向，所以要分两种情况讨论.若点A向右平移2个单位得到点B，则点B坐标为B（a+2，b），由关于原点的中心对称坐标性质得点D的坐标为D（-a-2，-b），同理得点A向左平移时点D的坐标为D（2-a，-b）.故答案为（-2-a，-b）或（2-a，-b）.平行四边形的顶点坐标问题可以转化为中心对称问题.一般地，结合点平移变换的坐标性质可得平行四边形一对对角顶点横坐标的和与另一对对角顶点横坐标的和相等，对角顶点的纵坐标也有类似结论，应用此结论可以解决平行四边形顶点坐标分类讨论的问题.

二、典型解法评析

平面直角坐标系如舞台，演绎几何图形与代数关系，如网，包罗数学万象.在《标准》中图形与坐标知识条目虽然只有两大类：坐标与图形位置、坐标与图形运动.但实际考查中却是复杂多变，涉及知识点丰富，综合性强，考查的内容与能力要求的跨度较大，既涉及基础知识的考查，又涉及综合探究能力的考查，要求学生要有扎实的基础知识和熟练运用各类知识的能力，要关注图形几何观念的发展及图形运动过程中数学思想方法的渗透，感悟图形静止或运动中形与量的联系，学会在平面直角坐标系中分离提取基本图形，结合坐标将数形结合发挥极致.下面就对2016年中考“图形的变化”问题的典型解法进行整理、归纳，以期能对读者有所启发.

（一）提取模型，对称转化

例12（江苏·苏州卷）矩形OABC在平面直角坐标系中的位置如图14所示，点B的坐标为B（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（ ）.

图14

图15

【解法点拨】此题考查平面直角坐标系中周长最小值的动点坐标的确定，试题中含有一个基本模型——“将军饮马”问题，由已知条件知CD为定值，CE与DE的长可变，因此问题转化为直线AB外两个定点C，D与直线AB上一点距离和的最小值问题.显然只需将点C或点D作出关于AB的对称点，结合两点间线段最短即可求解.如图15，作点D关于AB的对称点，所以直线CH解析式为当x=3时，，即有当点E的坐标为时，△CDE的周长最小.故选B.此题的解决经历了以下过程：三角形周长最小值问题转化为直线同侧两线段和最小值问题，再转化为直线两侧线段和最小值问题.从解题过程中可以看到，转化思想有利于确定解题策略，基本图形或模型的分离提取有利于快速确定解题方案.

（二）等长线段，等量方程

例13（广东·茂名卷）如图16，抛物线y=-x2+bx+c经过A（-1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．

（1）求经过A，B，C三点的抛物线的函数表达式；

（2）点P是线段BD上一点，当PE=PC时，求点P的坐标；

（3）在（2）的条件下，过点P作PF⊥Ox于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以点F，M，G，N为顶点的四边形是正方形时，求出点M的坐标．

图16

图17

图18

【解法点拨】此题以二次函数图象为背景，设计两个考查有关线段相等的问题.第（1）小题较为简单，应用交点式可得.第（2）小题涉及平面内两点间距离问题，虽然初中没有学习过两点间距离公式，但可以构造直角三角形，结合勾股定理表示出线段PC，PE的长.如图17，由直线BD的解析式为y= -2x+6，可设点P的坐标为P（t，-2t+6），过点P作PH⊥OC，PF⊥OB，又因为PC2=PE2，所以有t2+（3+ 2t-6）2=（t-1）2+（-2t+6）2.解得t=2.所以点P的坐标为P（2，2）；第（3）小题要求确定正方形的顶点M（a，0）的坐标要分类讨论，因为点M可能在直线NF的左侧，也可能位于直线NF的右侧，点N可能在x轴上方，也可能在其下方，化繁为简，去掉图中无关元素得到图18，若四边形MGNF为正方形，则有MF=MG，即有去掉绝对值，化为两个方程①2-a=a2-2a-3；②a-2=a2-2a-3，解得或.所以当以点F，M，N，G为顶点的四边形是正方形时，点M的坐标为此题中第（2）小题为坐标系中线段等长问题，由于线段不与坐标轴平行，可以构造直角三角形结合勾股定理表示线段长，其中线段等长即是等量关系，设元列方程即可求解；第（3）小题中的正方形的本质还是线段等长，且这两条线分别与坐标轴平行，线段长可用点横坐标差或是纵坐标差表示，由于动点问题要分类，稍微复杂一些，但只要抓住问题本质线段等长这一等量关系，设元并将未知的线段长用含未知数的代数式表示，根据等量关系列出方程即可求解，此为通法，可见根据等量关系建立关于横（纵）坐标的方程是平面直角坐标系中求符合一定条件的点的坐标的重要方法.

（三）共点旋转，类比构造

例14（河南卷）（1）发现：如图19（1），点A为线段BC外一动点，且BC=a，AB=b．

填空：当点A位于_______时，线段AC的长取得最大值，且最大值为______（用含a，b的式子表示）.

（2）应用：点A为线段BC外一动点，且BC=3，AB=1，如图19（2）所示，分别以AB，AC为边，作等边△ABD和等边△ACE，连接CD，BE．

①试找出图中与BE相等的线段，并说明理由；

②直接写出线段BE长的最大值．

（3）拓展：如图19（3），在平面直角坐标系中，点A的坐标为A（2，0），点B的坐标为B（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，直接写出线段AM长的最大值及此时点P的坐标．

图19

【解法点拨】此题考查平面直角坐标系一定条件下的线段长的最大值的确定，试题设计了第（1）小题引导学生学习确定共点线段另两个端点距离的最大值，较为简单；第（2）小题在第（1）小题的基础上引导学生发现共顶点等边三角形中两个顶点距离的最大值；第（3）小题是在第（2）小题的基础上，将问题放置在平面直角坐标系中，类比第（2）小题的方法构造共顶点等腰直角三角形探究两顶点距离的最大值.三个问题层层递进，层层铺垫，是一道学习型的试题，学生在解题中学习，在学习中解题，一方面，考查数学知识应用能力；另一方面，也考查学生的数学学习能力.第（1）小题根据点A位于CB的延长线上时，线段AC的长取得最大值a+b；第（2）小题中问题①根据等边三角形的性质得到AD=AB，AC=AE，∠BAD=∠CAE=60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD=BE；问题②由①知线段BE长的最大值等于线段CD的最大值，由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，所以BE的最大值为BD+BC=AB+ BC=4；对于第（3）小题，如图20（1），连接BM，将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，得到△APN是等腰直角三角形，根据全等三角形的性质得到PN=PA=2，BN=AM，根据当点N在线段BA的延长线上时，线段BN取得最大值，即可得到最大值为；如图20（2），过点P作PE⊥Ox于点E，根据等腰直角三角形的性质即可得此题是基于一个基本图形与结论的应用而命制的，即两个有公共对应点相似的等腰三角形中，一般存在另一对三角形全等，这一对全等三角形也可看成是公共点旋转而成的.也是俗称“手拉手型三角形”的一种特殊情况（全等），在问题解决中如果能认识到这一结论，就可类比第（2）小题，在第（3）小题中构造一个以点P为公共顶点的等腰直角△APN，图中就浮出另一对全等△APM与△NPB，其中△NPB可以看成△APM绕点P旋转而得.从此题的解决，可以感受到数学学习要重视基本图形的归纳与总结，要关注类比思想的应用，在平时要积极主动地积累解题活动经验.

图20

（四）直角分类，构造K型

例15（浙江·湖州卷）如图21，已知二次函数y=-x2+bx+c（b，c为常数）的图象经过点A（3，1），点C（0，4），顶点为点M，过点A作AB∥Ox，交y轴于点D，交该二次函数图象于点B，连接BC．

（1）求该二次函数的解析式及点M的坐标；

（2）若将该二次函数图象向下平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；

（3）点P是直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似，试直接写出所有点P的坐标（直接写出结果，不必写解答过程）．

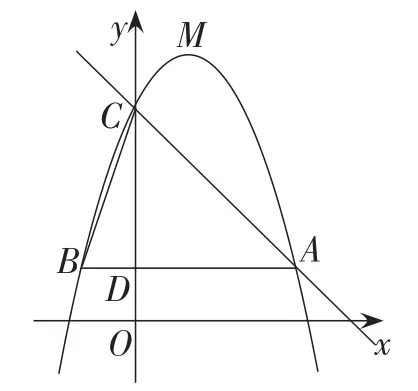
图21

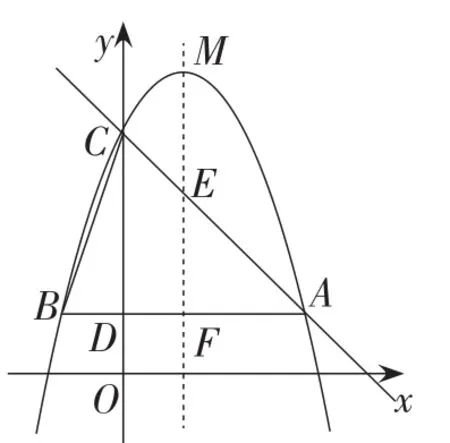
图22

【解法点拨】此题考查二次函数解析式求法及抛物线的平移和直角三角形的相似分类讨论，三道小题都涉及坐标点的确定.第（1）小题较为基础，二次函数解析式为y=-（x-1）2+5，点M的坐标为M（1，5）.第（2）小题中要确定m的取值范围，可转化为抛物线对称轴被△ABC所截得的线段EF的两端点E，F纵坐标的确定（如图22），易得2＜m＜4.第（3）小题为相似三角形的分类讨论，由已知可得△BCD为直角三角形，且BD∶CD=1∶3，又因为CM⊥AC，若点P，点C，点M所构成的三角形与△BCD相似，可按PC∶CM=1∶3或PC∶CM=3∶1分类讨论，而点P在AC上，可能在点C的左侧或右侧，所以共需分四种情况讨论.①当点P在点C的左侧且PC∶CM=3∶1时（如图23（1）），由∠PCM=90°，过直角顶点C作EF∥Ox，过点P，M分别作PF⊥EF于点F，ME⊥EF于点E，则△CEM∽△PFC，且相似比为1∶3.由CE=ME=1，得PF=CF=3.所以点P的坐标为P（-3，7）.②当点P在点C的左侧且PC∶CM=1∶3时（如图23（2）），类似得点P为③当点P在点C的右侧且PC∶CM=1∶3时（如图23（3）），类似得点P为；④当点P在点C的右侧且PC∶CM=3∶1时（如图23（4）），类似得P（3，1）.故所有符合题意的点P的坐标有4个，分别为P1（-3，7），

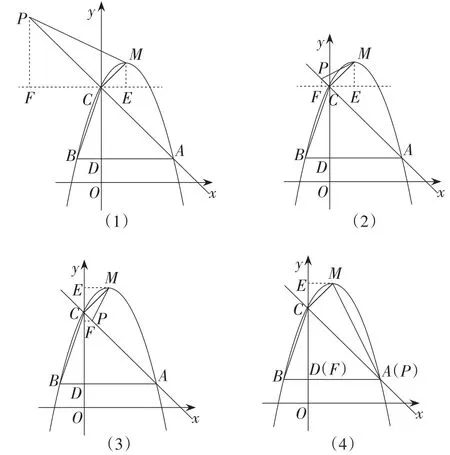
图23

从第（3）小题中可以看到在平面直角坐标系中，遇到直角问题，可借助坐标轴（如③④）或经过直角顶点与坐标轴的平行线（如①②）构造三垂直（即K型图）基本图形，可以化难为易，这里直角问题，可以是平面直角坐标系中直角三角形相似的分类讨论，也可以以动点何时为直角进行讨论，还可以是矩形（正方形）的分类讨论，或是直角边比给定的（如m∶n型）直角三角形的分类讨论，或是特殊角的直角三角形（如含30°角的直角三角形）的分类讨论，还有旋转90°的运动变换等，都可以构造三垂直寻找数量关系.若是问题中图形是非直角的特殊角，如两边长为1∶3且两边的夹角为60°的三角形顶点坐标的确定，可以类似直角构造三垂直的方法依托坐标轴或其他直线构造三等角基本图形来解决.

三、试题解法欣赏

中考命题追求试题的灵动，鼓励学生用不同方法求解，命题者独具匠心，解法亦是精彩纷呈.现摘录一二，供大家教学参考.

例16（湖北·武汉卷）抛物线y＝ax2＋c与x轴交于A，B两点，顶点为点C，点P为抛物线上且位于x轴下方的点．

（1）如图24（1），若P（1，－3），B（4，0）.

① 求该抛物线的解析式；

② 若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；

（2）如图24（2），已知直线PA，PB与y轴分别交于E，F两点．当点P运动时，是否为定值？若是，试求出该定值；若不是，说明理由．

图24

②如图25，若点D在点P左侧，由∠DPO＝∠POB，得DP∥OB，点D与点P关于y轴对称.由P（1，-3），得D（-1，-3）.

如图26，若点D在点P右侧，即图中点D2，则∠D2PO＝∠POB.延长PD2交x轴于点Q，则QO＝QP.设Q（q，0），则（q－1）2＋32＝q2.解得q＝5.所以点Q的坐标为Q（5，0）.则直线PD2为.求交点得.综上可得，点D的坐标为D（-1，-3）或

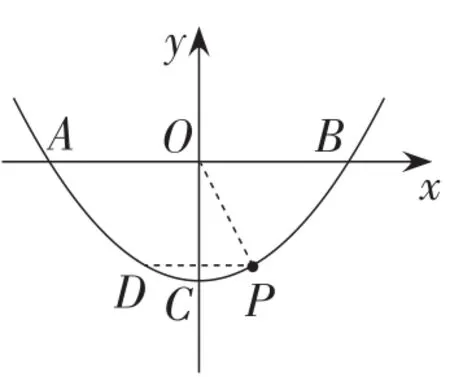
图25

图26

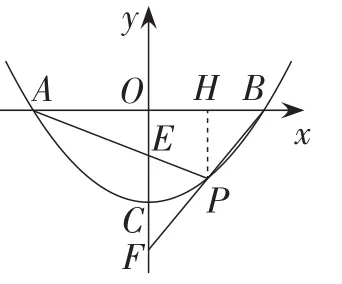
图27

例17 （浙江·杭州卷）如图28，已知四边形ABCD和四边形DEFG为正方形，点E在线段DC上，点A，D，G在同一直线上，且AD=3，DE=1，连接AC，CG，AE，并延长AE交CG于点H．

（1）求sin∠EAC的值．

（2）求线段AH的长．

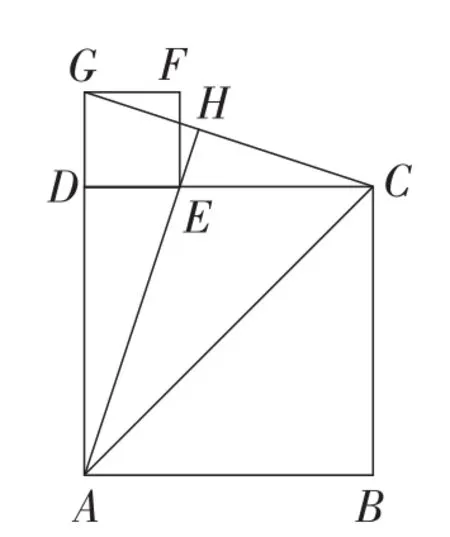
图28

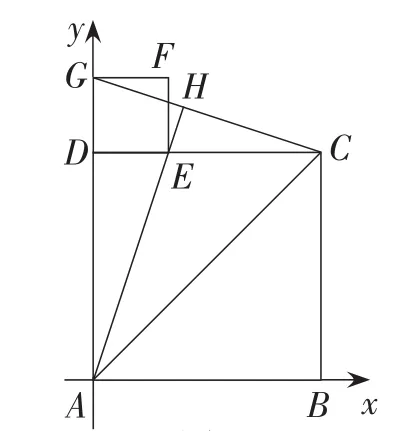
图29

【解法点拨】此题没有平面直角坐标系，应用全等及等积或相似即可解，但此题也可以采用解析法求解.不妨以点A为坐标原点，以AB为横轴正方向，AG为纵轴正方向建立平面直角坐标系（如图29），由E（1，3）得直线OE解析式为y=3x，由点C为C（3，3），G为G（0，4）得到直线CG解析式为联立方程组可求得交点H为所以可以发现，此题虽不复杂，但建立直角坐标系用解析式也是别有一番风味，也为解析法求几何问题提供了一种思路.数学试题的设计常常会将几何问题结合平面直角坐标系融入数形结合思想，从数、形两方面合作研究几何问题，但在解题时在几何问题中添加平面直角坐标系应用解析法求解并不常用，似乎有些厚此薄彼的感觉，有失偏颇.解析法解几何问题在平时的教学中值得关注，有些几何图形建立直角坐标系后思考会有意想不到的收获.

［1］中华人民共和国教育部制定．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

［2］李兴梅.2015年中考数学试题“图形与坐标”专题解题评析［J］.中国数学教育（初中版），2016（1/2）：112-126.

［3］周宁，叶茂恒.2015年中考数学试题“图形的变化”专题解题评析［J］.中国数学教育（初中版），2016（1/2）：92-102.

［4］张晋华，薛红霞.2014年中考数学试题“图形与坐标”分类解析［J］.中国数学教育（初中版），2015（1/2）：86-97.

［5］景敏，陈丽敏，王瑾.2013年中考数学试题分类解析：图形与几何［J］.中国数学教育（初中版），2014（1/2）：63-82.

2016—12—26

叶茂恒（1975—），男，中学高级教师，主要从事数学课堂教学与初中数学命题研究.