一种基于相位噪声的大规模MIMO预编码算法

王 军，戴建新，程崇虎，汪 鹏，李 莎

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 理学院，江苏 南京 210023)

一种基于相位噪声的大规模MIMO预编码算法

王 军1，戴建新2，程崇虎1，汪 鹏1，李 莎1

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 理学院，江苏 南京 210023)

在大规模MIMO系统中，使用廉价的硬件会带来一些问题，本地振荡器引起的相位噪声就是其中之一。相位噪声会影响到基站侧对CSI的估计，使得在信号发送过程中的CSI不同于估计的CSI，然而预编码矩阵的设计依赖于CSI，最终影响到基站侧对信号的处理导致系统性能的下降。针对大规模MIMO系统中存在的廉价的本地振荡器引起的相位噪声这一问题，通过分析其对信号以及CSI的影响，提出一种基于相位噪声的预编码算法。通过仿真结果得出，当基站侧不存在相位噪声时，提出算法和传统预编码算法有着相同的性能。但是当基站侧存在相位噪声时，提出算法优于传统预编码算法。从而可以得出结论，当基站侧存在相位噪声时，提出算法一定程度上降低了其对系统的影响程度。

大规模MIMO；相位噪声；预编码算法；CSI估计；振荡器

0 引 言

为了满足人们对服务质量和数据速率不断提高的需求，提出了一些新的无线通信技术，其中大规模MIMO(Multiple-Input Multiple-Output，多输入多输出)技术就扮演着重要角色。而且，大规模MIMO技术已被纳入下一代移动通信系统中的关键技术之一，其使得中心基站或者分布式基站侧装有上百根天线，从而大大提高了通信速率和服务质量[1-4]。

虽然大规模MIMO技术能带来很多好处，但是由于同时服务多个用户，使得用户间干扰也随之增大[1]。现今，有很多技术可以抑制用户间干扰，比如在基站侧采用预编码技术[5]。文献[6]提出迫零(Zero Forcing，ZF)线性预编码算法，利用信道求逆来实现预编码。文献[7]提出块对角化(Block Diagonalization，BD)预编码算法，通过奇异值分解获得各用户相对于其他用户的正交基，从而把多用户MIMO信道分解成并行的互不干扰的单用户信道。

以上所述的预编码算法都是以理想的硬件为前提，现实中这几乎不可能。由于在大规模MIMO系统中，廉价硬件的使用影响到系统的整体性能，比如有噪声的本地振荡器引起的相位噪声就是非理想硬件带来的问题之一[8-10]。相位噪声的存在会导致信道状态信息(Channel State Information，CSI)估计的误差，使得在传输信号期间的CSI不同于基站侧估计到的CSI，导致系统性能的下降[9-10]。因此，有必要研究因本地振荡器引起的相位噪声对系统性能的影响状况。

近年来，对于相位噪声的研究做出了很多努力。例如，文献[8-10]研究了在大规模MIMO系统中，相位噪声对上行性能的影响。文献[11-12]研究得出，除加性高斯白噪声以外，本地振荡器对于CSI的估计有着很大影响。文献[13]研究了在单输入单输出系统中，相位噪声对信号到达方向估计的影响。然而，通过预编码方法来消除大规模MIMO中下行链路的相位噪声还是比较少的。

文中研究了在大规模MIMO系统下行链路中，本地振荡器引起的相位噪声对系统性能的影响，同时采用预编码技术消除这种影响。由文献[8]可知，在下行链路中，基站侧和用户侧都存在相位噪声。为了分析方便，只考虑基站侧的相位噪声。同时假设在时分双工(Time Division Duplex，TDD)的工作方式下，基站侧每一根天线都和一个振荡器相连，从而每根天线上的相位噪声都是不同的。在以上假设下，分析相位噪声对CSI的影响，提出一种对传统预编码改进的算法并对其进行仿真。

1 系统模型

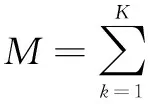
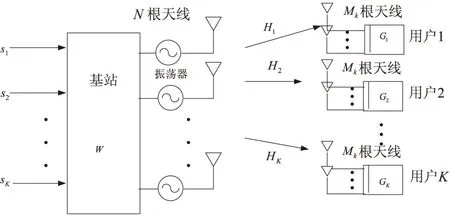
图1 系统模型

图中，Hk∈CMk×N是第k位用户的信道矩阵，其每个元素都是均值为0、方差为1的高斯复随机变量；W∈CN×M是所有用户的预编码矩阵，不同的预编码方案会得到不同的预编码矩阵；sk∈CMk×Lk是第k位用户在预编码前的信号向量，Lk代表信号向量的长度；Gk∈CMk×Lk是第k位用户的信号检测矩阵。

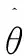
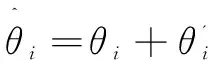
(1)

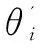
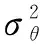
因此，可得基站第i根天线到第k位用户的有效信道为：

(2)

其中，hk,i(i∈{1,2,…,N})为复物理信道。

至此，可以得出所有用户接收到的信号Y。

(3)

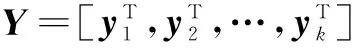
E{‖Ws‖2}=PT

(4)

2 基于相位噪声的预编码算法

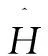
文中通过这个理念提出基于相位噪声的迫零(PhaseNoiseZeroForcing，PN-ZF)和基于相位噪声的块对角化(PhaseNoiseBlockDiagonalization，PN-BD)预编码算法。

2.1 PN-ZF预编码算法

由文献[6]可知，PN-ZF预编码矩阵WPN-ZF为：

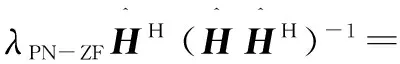
(5)

其中，λPN-ZF是满足式(4)的功率因子。

2.2 PN-BD预编码算法

设第k位用户的预编码矩阵为WPN-BD,k=λPN-BDWk1Wk2Γk[7]。其中，Wk1∈CN×Dk主要是用来消除用户间的干扰；Wk2∈CDk×Lk主要是把第k位用户的信道分成平行子信道；λPN-BD是用来满足式(4)的功率因子；Γk∈CLk×Lk是对角化功率加载矩阵。下面，介绍Wk1和Wk2的计算方法。

由式(3)，可得第k位用户接收的信号yk为：

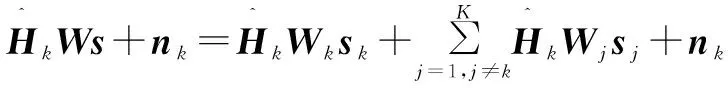
(6)

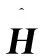
由式(6)知，只要满足式(7)，那么就能消除用户间的干扰。

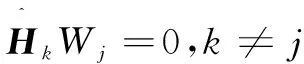
(7)

此时，第k位用户接收的信号yk为：

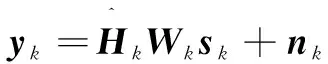
(8)

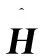
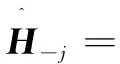
(9)

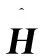
(10)

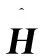
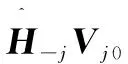
(11)

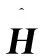
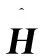
(12)

至此，可以得出所有用户的预编码矩阵和检测矩阵：

(13)

(14)

2.3 和速率分析

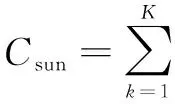
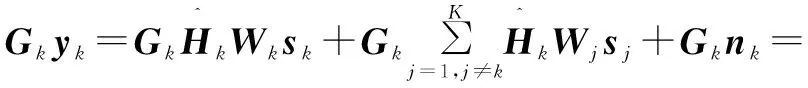
(15)

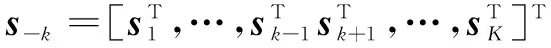
由信息论的知识可以得出，第k位用户的数据速率为：

(16)

其中，Rxx表示x的自相关函数。

因此，可以得出：

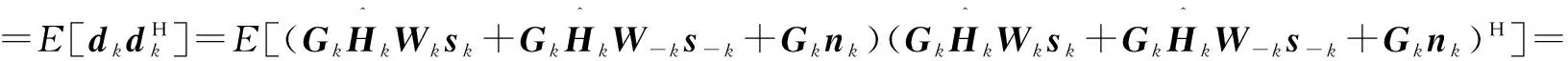
(17)

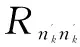
(18)

故，可得：

CPN-BD,k=

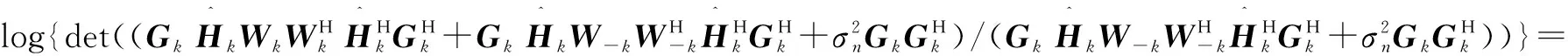
(19)

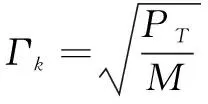
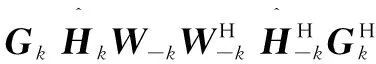
CPN-BD=

(20)

当不存在相位噪声时，由文献[18]可知BD预编码下，第k位用户的数据速率为：

(21)

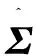
(22)

3 数值仿真

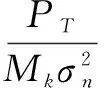
图2和图3显示了不同预编码算法在误码率(BitErrorRatio，BER)上的比较。

由图2可以看出，当不存在相位噪声时，文中算法和传统预编码算法有着相同的性能。同时由图3可以看出，文中算法优于传统预编码算法，尤其是在高信噪比的时候。

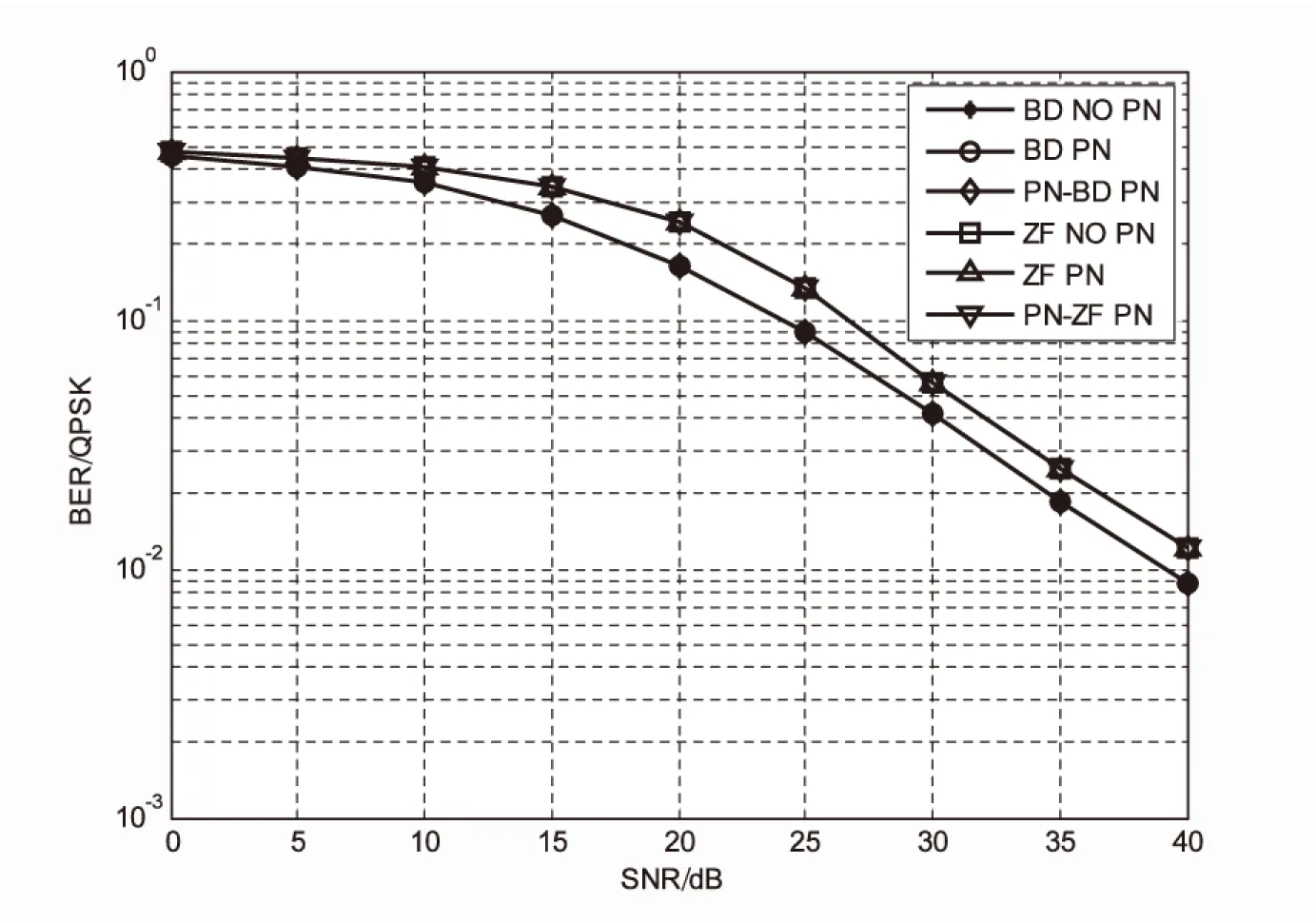
图2 不同预编码算法在BER上的比较=0°)

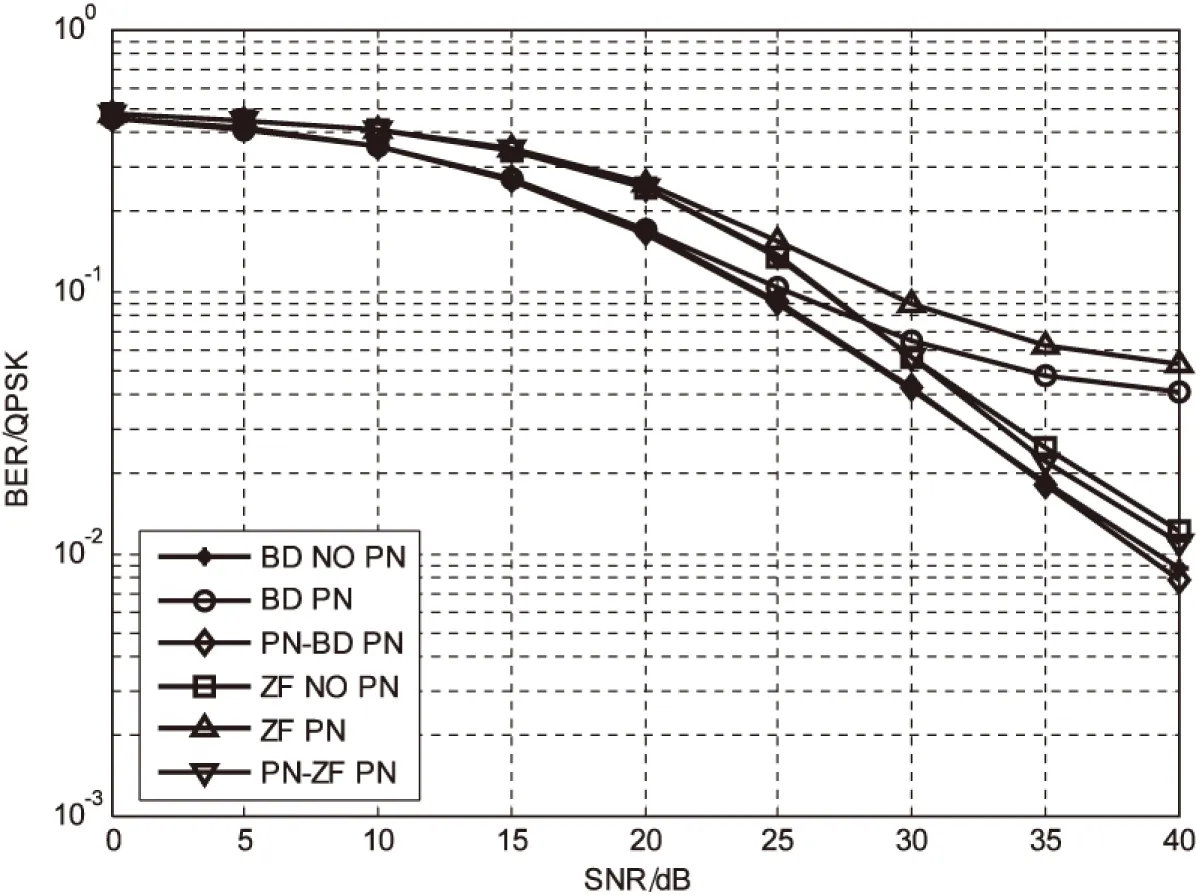
图3 不同预编码算法在BER上的比较=3°)

图4显示了当存在相位噪声时，不同预编码在和速率上的比较。

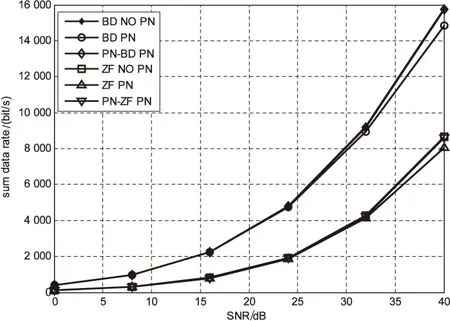
图4 不同预编码算法在和速率上的比较=3°)

可以看出，传统预编码的和速率会受到相位噪声的影响，而文中算法表现出了很好的优势，尤其在高信噪比的情况下。

4 结束语

针对大规模MIMO中本地振荡器存在的相位噪声问题，通过研究相位噪声对系统性能的影响，分析传统预编码的不足，提出一种基于相位噪声的预编码算法。仿真结果表明，在误码率方面，当基站侧不存在相位噪声时，文中算法和传统算法有着相同的性能。当基站侧存在相位噪声时，文中算法较优于传统算法，且随着信噪比的不断增大，文中算法所表现出来的性能更佳。同时，在和速率方面，文中这算法相比传统算法也具有很大的优势。下一步的研究方向就是考虑用户端存在相位噪声和时变的相位噪声的场景。

[1]LuL,LiG,SwindlehurstAL,etal.AnoverviewofmassiveMIMO:benefitsandchallenges[J].IEEEJournalofSelectedTopicsinSignalProcessing,2014,8(5):742-758.

[2]RusekF,PerssonD,LauBK,etal.ScalingupMIMO:opportunitiesandchallengeswithverylargearrays[J].IEEESignalProcessingMagazine,2013,30(1):40-60.

[3]LarssonE,EdforsO,TufvessonF,etal.MassiveMIMOfornextgenerationwirelesssystems[J].IEEECommunicationsMagazine,2014,52(2):186-195.

[4]deLamareRC.MassiveMIMOsystems:signalprocessingchallengesandfuturetrends[J].InformationTheory,2013,32(7):183-188.

[5]CaireG,ShamaiS.OntheachievablethroughputofamultiantennaGaussianbroadcastchannel[J].IEEETransactionsonInformationTheory,2003,49(7):1691-1706.

[6]PeelCB,HochwaldBM,SwindlehurstAL.Avector-perturbationtechniquefornear-capacitymultiantennamultiusercommunication-partI:channelinversionandregularization[J].IEEETransactionsonCommunications,2005,53(1):195-202.

[7]SpencerQH,SwindlehurstAL,HaardtM.Zero-forcingmethodsfordownlinkspatialmultiplexinginmultiuserMIMOchannels[J].IEEETransactionsonSignalProcessing,2004,52(2):461-471.

[8]BjornsonE,HoydisJ,KountourisM,etal.MassiveMIMOsystemswithnon-idealhardware:energyefficiency,estimation,andcapacitylimit[J].IEEETransactionsonInformationTheory,2014,60(11):7112-7139.

[9]KrishnanR,KhanzadiMR,KrishnanN,etal.OntheimpactofoscillatorphasenoiseontheuplinkperformanceinamassiveMIMO-OFDMsystem[J].IEEESignalProcessingLetters,2014,34(5):120-125.

[10]PitarokoilisA,MohammedSK,LarssonEG.Uplinkperformanceoftime-reversalMRCinmassiveMIMOsystemssubjecttophasenoise[J].IEEETransactionsonWirelessCommunications,2014,14(2):711-723.

[11]BaumDS,BolcskeiH.ImpactofphasenoiseonMIMOchannelmeasurementaccuracy[C]//IEEEvehiculartechnologyconference.[s.l.]:IEEE,2004:1614-1618.

[12]AlmersP,WyneS,TufvessonF,etal.EffectofrandomwalkphasenoiseonMIMOmeasurements[J].Technology,2005,1(1):141-145.

[13]KivinenJ,VainikainenP.Calibrationschemeforsynthesizerphasefluctuationsinvirtualantennaarraymeasurements[J].Microwave&OpticalTechnologyLetters,2000,26(3):183-187.

[14]KrishnanR,ColavolpeG,AlexandreGIA,etal.AlgorithmsforjointphaseestimationanddecodingforMIMOsystemsinthepresenceofphasenoiseandquasi-staticfadingchannels[J].IEEETransactionsonSignalProcessing,2013,63(13):1.

[15]KrishnanR,KhanzadiMR,KrishnanN,etal.LinearmassiveMIMOprecodersinthepresenceofphasenoise-alarge-scaleanalysis[J].IEEETransactionsonSignalProcessing,2015,13(3):11-19.

[16]RutmanJ.Characterizationofphaseandfrequencyinstabilitiesinprecisionfrequencysources:fifteenyearsofprogress[J].ProceedingsoftheIEEE,1978,66(9):1048-1075.

[17] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[18]SungH,LeeSR,LeeI.GeneralizedchannelinversionmethodsformultiuserMIMOsystems[J].IEEETransactionsonCommunications,2009,57(11):3489-3499.

A Linear Pre-coding Algorithm Based on Phase Noise in Massive MIMO

WANG Jun1，DAI Jian-xin2，CHENG Chong-hu1，WANG Peng1，LI Sha1

(1.College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications，Nanjing 210003,China；Abstract:In large scale MIMO system,the phase noise caused by local oscillator is one of the problems because of the use of cheap hardware.Phase noise will affect the estimation of CSI,which is different from the CSI of the process of sending signal.However,the design of pre-coding matrix is dependent on CSI and ultimately affects the signal processing from the base station side which leads to a decline in the performance of the system.Due to phase noise by cheap local oscillator in massive MIMO system,a pre-coding matrix is proposed by anglicizing the influence of phase noise on signal.The simulation results show that the proposed algorithm has the same performance as the traditional pre-coding algorithm when there is no phase noise in the base station.But when phase noise exists in the base station,the proposed algorithm is better than the traditional algorithm.So it can be concluded that the proposed algorithm can reduce the impact of the system to a certain extent when the phase noise exists in the base station.

large scale MIMO;phase noise;pre-coding algorithm;CSI estimation;oscillator

2016-04-13

2016-08-10

时间：2017-01-10

江苏省博士后科研资助计划(1501073B)；南京邮电大学自然科学基金(NY214108)

王 军(1991-)，男，硕士生，研究方向为大规模MIMO系统中的预编码；戴建新，博士，副教授，研究方向为5G移动通信系统的关键技术；程崇虎，博士，教授，研究方向为电磁场。

http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1028.064.html

TN929．5

A

1673-629X(2017)03-0103-05

10.3969/j.issn.1673-629X.2017.03.021