压缩感知中基于快速不动点迭代算法的研究

刘 艳,宋欢欢,李 雷

(南京邮电大学 非结构化数据计算理论与应用研究中心,江苏 南京 210046)

压缩感知中基于快速不动点迭代算法的研究

刘 艳,宋欢欢,李 雷

(南京邮电大学 非结构化数据计算理论与应用研究中心,江苏 南京 210046)

针对传统迭代算法在解决大规模问题时速度较慢的问题，在介绍了压缩感知中重构的基本模型以及传统不动点迭代方法(FPC)的基础上，提出了一种新的重构算法-快速不动点迭代方法(FFPC)。传统的不动点迭代方法其实是基于算子分裂的方法。为了提高去重构性能，通过引入软阈值和正则化参数的双收缩，逐步迭代恢复原始图像信号，以加快算法的收敛速度，减小重构误差，从而改善图像的重构质量。仿真结果表明，在相同的实验环境下，与传统的不动点迭代算法以及其他算法相比，快速不动点迭代算法重构图像的峰值信噪比较高，相对误差较小，在低采样率下运行时间较少，性能最优。

压缩感知；图像重构；传统不动点迭代算法；快速不动点迭代算法；收敛速度；重构质量

1 概 述

压缩感知[1]理论指出：对可压缩的信号可通过远低于Nyquist标准的方式对数据进行测量，仍能够精确地恢复出原始信号。压缩感知理论的基本原则和目标就是从较少的相对不完整的测量值b=Ax中恢复出K稀疏的信号x∈Rn。理论上，恢复信号x最简单的方法，是求解下面的l0范数最小化问题

(1)

其中，‖x‖0表示x中非零元素的个数。

但是l0范数模型(1)是NP难题[2]，在实践上不可行。因此，Candes等[3-5]、Donoho等[6]指出，在一定条件下，问题的解x∈Rn通过解式(2)获得：

(2)

详细信息见文献[3,7-16]。

优化算法通过解问题(2)或者与其相近的l1范数最小二乘问题来找到问题(1)的解。

(3)

其中，μ>0。

不动点连续(FPC)方法主要解决l1范数问题。

(4)

其能够解决大规模问题。

基于不动点迭代方法，文中提出了一种收敛速度更快、算法性能更优的新算法-快速不动点迭代方法。实验结果表明，该算法表现出了最优的性能。

2 FPC方法理论基础

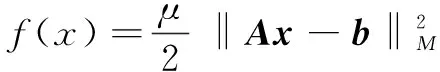
0∈T(x)⟺0∈(x+τT1)-(I-τT2)⟺ (I-τT2)x∈(I+τT1)x⟺x=(I+τT1)-1(I-τT2)x

(5)

由式(5)，通过使用向前向后分裂算法即可找到算子T的零点。

xk+1=(I+τT1)-1(I-T2)xk

(6)

至此，得到了不动点迭代式(6)。对于凸优化问题(4)，令T2=f(x)。

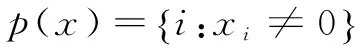
g(x)=

(7)

|E|表示集合E的势；λi(M),i=1,2,…,n，λmax(M)和λmin(M)分别表示矩阵的最大特征值和最小特征值。

对于t∈R，用符号函数表示。那么，|t|的次微分即可用集值函数来表示：

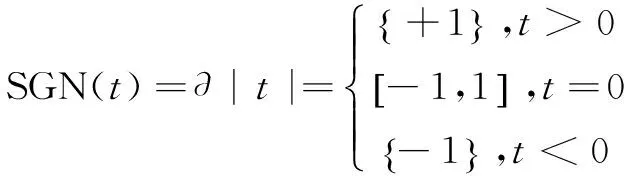
(8)

因此，对于向量x∈Rn，定义sgn(x)∈Rn和SGN(x)∈Rn，其中(sgn(x))i=sgn(xi)，(SGN(x))i=SGN(xi)，显然有：

sgn(x)=sgn(x')⟺SGN(x)=SGN(x'),∀x,x'

(9)

接着，对于凸规划(4)的最优性和最优解集，假设X*是Φ(x)的最优解集。由凸分析[17]可知最优性条件为：

x*∈X*⟺0∈SGN(x*)+g(x*)

(10)

或者，等价表示为：

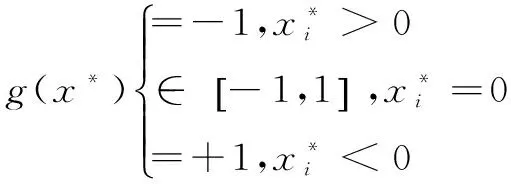
(11)

由式(11)可知，若‖g(0)‖∞≤1,则0是凸优化(4)的一个最优解，即

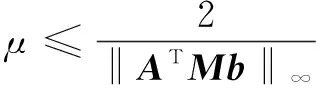
(12)

因此，可以很方便地检测凸优化(4)是否有零解。

命题1：X*是Φ(x)的最优解集，对于∀τ>0,x*∈X*，当且仅当

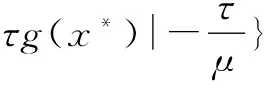
(13)

方程(13)是由两个Rn→Rn映射组成，定义如下：

h(·)=I(·)-τg(·)

(14)

(15)

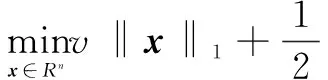
(16)

令向前向后分裂推导出的式(6)中的T1(x)=∂‖x‖1,T2(x)=g(x)，即可直接得出式(6)与式(16)是等价的。

3 快速不动点迭代(FFPC)方法

3.1 FFPC算法思想

FFPC算法求解的是问题(4)的等价表示：

(17)

其中，μ是引入的正则化参数，用来平衡l1,l2范数所占的比重，利用优化算法可求得最优解x*。

(18)

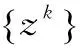
(19)

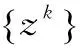
使用式(19)更新x类似于使用最快下降方法。

Φ(xk+1)=Φ(xk-tktkΦ(xk))

(20)

在满足式(20)的基础上，受文献[18]的启发，使用式(21)来寻找最优步长tk。

(21)

因此式(16)可更新为：

xk+1=Sv∘h(zk)=sgn(zk-τg(zk))⊙max{|zk- τg(zk)|-τμ,0}

(22)

由于阈值v=τμ影响了不动点迭代式(21)的收敛速度，v越大，收敛速度越快。则只要使得τ，μ的取值尽量大，就可以加快不动点迭代式(22)的收敛速度。使用BB(Barzilai和Borwein)步长更新参数τ：

(23)

对于正则化参数μ，其作用是平衡二次函数f(x)和l1范数‖x‖1的比重。为使式(17)侧重于保证项f(x)最小，通常选取μ=δ·max(ATb)(δ是大于0的常数)作为初始值。在迭代过程中，为了使x快速稀疏，对μ作适当收缩，令μ=αμ(其中α是收缩因子，0<α<1)，平衡二次函数f(x)和l1范数‖x‖1在迭代过程中的比重。

快速不动点迭代方法的迭代停止条件是由x的两次相邻迭代的相对误差决定的。

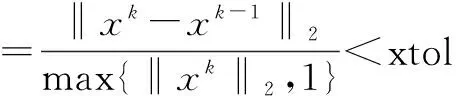
(24)

终止条件为xtol和gtol，当满足上述终止条件时，停止迭代。

3.2 FFPC方法的收敛性证明

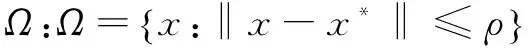
(25)

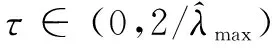
‖h(x)-h(x')‖≤‖x-x'‖

(26)

此外，当g(x)=g(x')时，式(26)依然成立。

由引理1可知，算子h(·)是非扩张的，根据FPC算法的q1阶线性收敛性质，可以判定文中FFPC的迭代式(22)是全局收敛的。

引理2：对于k>1，FFPC算法产生的序列{xk,zk}满足：

‖xk+1-xk‖≤‖xk-xk-1‖,‖zk+1-zk‖≤ ‖zk-zk-1‖,x*=z*

(27)

‖S(zk+1)-S(zk)‖≤‖zk-zk-1‖

(28)

又由式(22)可知zk+1=S(zk+1)，故

‖zk+1-zk‖=‖S(zk)-S(zk-1)‖≤‖zk-zk-1‖

(29)

证毕。

3.3 算法描述

FFPC算法步骤如下：

Step1：令信号在小波域的变换稀疏为x0=0，初始化迭代次数k=1,t1=1,z1=0。

Step2：利用式(16)计算xk。

Step3：计算tk+1，根据式(19)对t进行更新，利用式(17)计算zk。

Step4：按照式(22)计算迭代终止函数值Gk(xk,xk-1)，如果满足迭代终止条件，则令x*=xk，否则执行Step5。

Step5：扩张正则化参数μ=αμ，更新迭代次数k=k+1，更新τ，将zk带入Step2，重复上述过程。

迭代结束后，得到的迭代结果x*即是对原始信号的估计值。

3.4 除 偏

FFPC算法重构的信号存在一些误差，采用除偏(Debiase)方法来去除误差比较大的元素，使得非零的系数个数不超过m。FFPC算法和FPC算法类似，当输入信号绝对稀疏时，使用除偏过程能够使得算法FFPC重构信号的精度更高。

Debiase算法：

输入参数：FFPC算法中的测量矩阵A，测量信号b和原始信号x。

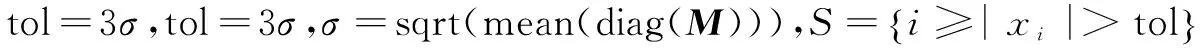
若1≤|S|≤m，那么

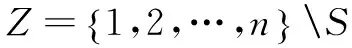
xz=0

否则，停止计算。

4 仿真实验和结果分析

为了说明提出算法的优越性，使用Matlab对提出的快速不动点迭代方法进行实验。为了比较客观地说明FFPC算法的有效性，将FFPC的实验数据与IST算法、FIST算法、贪婪算法CoSaMP、子空间追踪SP算法以及不动点连续方法的结果进行比较，分别从信号重构时间、相对误差和峰值信噪比三个方面进行比较。

图1(a)为各个算法重构时间随采样率的变化曲线。从中可见，文中提出的FFPC算法，重构Camera图像的速度最快，充分体现了FFPC算法的速度及稳定性。此外，图1(b)和图1(c)则展示了这5种算法重构信号的质量，图1(b)中不动点系列算法的相对误差都较小，FFPC算法的准确性和FPC算法接近，而图1(c)中FFPC算法重构出来的信号的信噪比比较高。

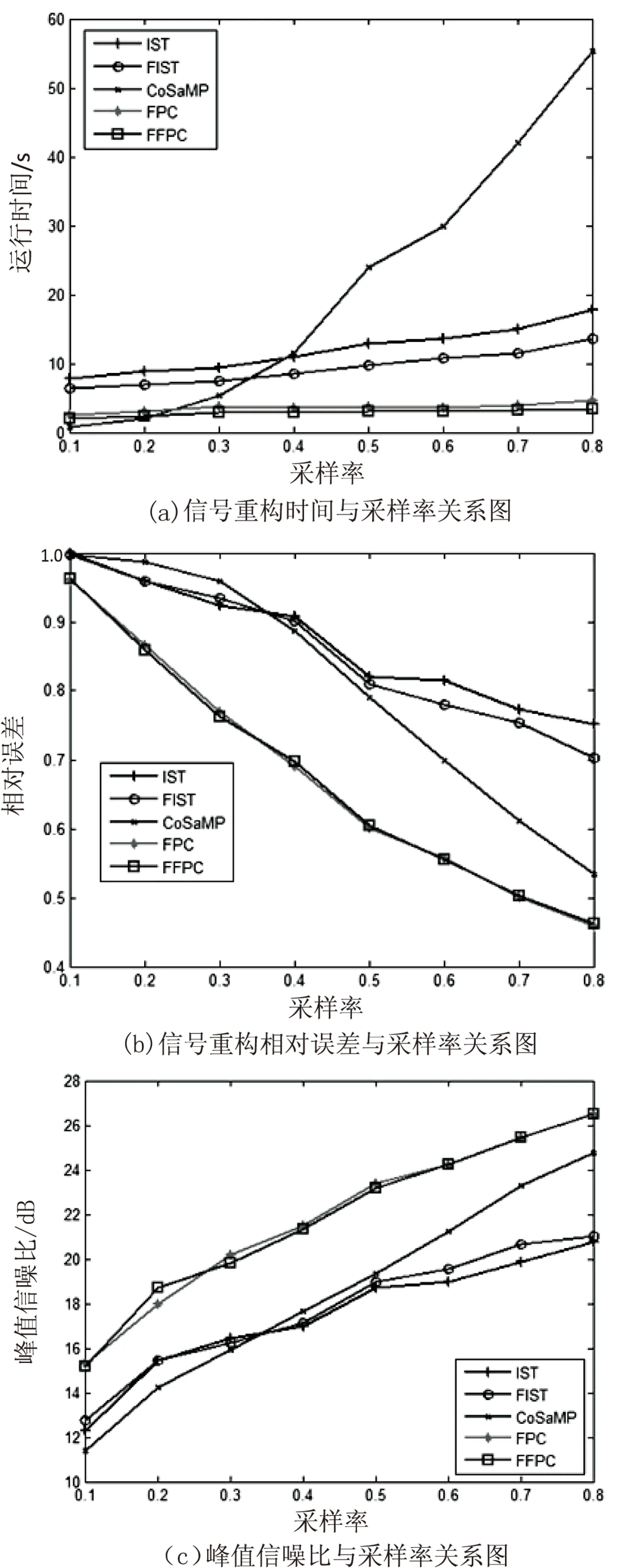
图1 FFPC算法性能随采样率变化图

Camera图像处理结果如表1所示。

如表1所示，在重构Camera图像所用的时间上，FFPC算法的重构速度最快。例如，在采样率为0.5时，FFPC算法比FIST和FPC算法分别快了4s和0.781 3s；在重构误差方面，FFPC算法的效果也很好，在采样率为0.25和0.75时，重构误差均最小，其他情况下，误差值均与FPC算法接近；在图像重建质量方面，FFPC重构信号的峰值信号比也比IST、FIST和CoSaMP高出很多，信号重建质量与FPC算法相近。

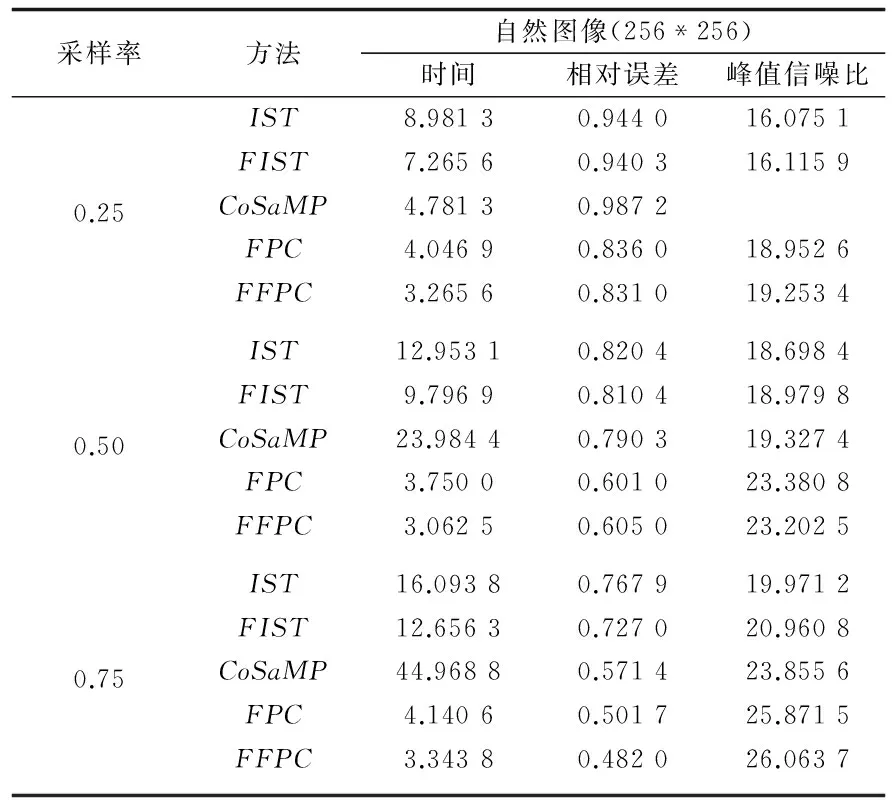
表1 Camera图像处理结果

图2给出了使用FFPC算法在采样率为0.25,0.5和0.75时对自然图像的重构效果。

图2 FFPC算法对自然图像的重构效果

FFPC算法在采样率为0.25时，重构出的图像中噪点较多。当采样率达到0.5时，重构出来的图像信号都比较清晰，噪点较少，视觉效果相对很好。

由于FPC和FFPC算法在求解大规模问题时，往往得到的稀疏解中非零系数的个数偏差较大，所以文中采用除偏的方式来处理FPC和FFPC算法得到的粗糙解，结果如表2所示。

与原来的重构结果相比，除偏后图像的峰值信噪比均有所提高。当采样率为0.25时，经过除偏操作后，FFPC算法重构自然图像的峰值信噪比和原来相比提高了1.843 6dB。

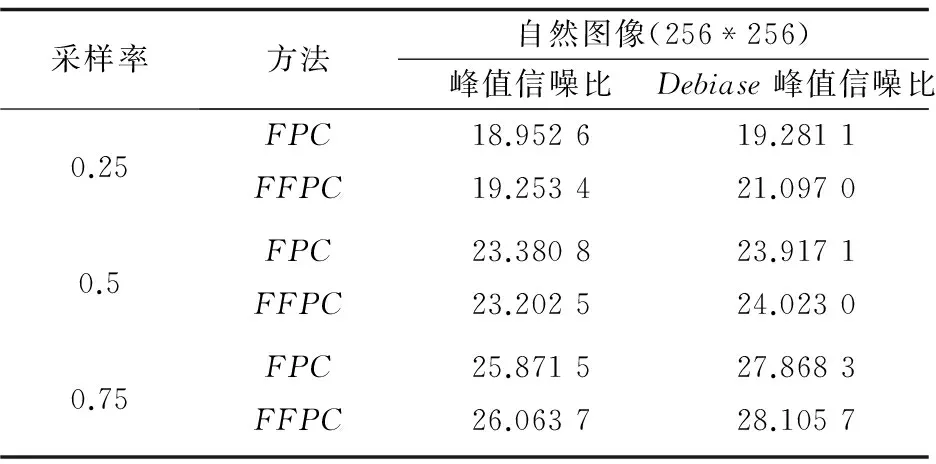
表2 图像除偏结果

图3给出了经过除偏操作后，自然图像Camera的重构效果。

图3 自然图像的Debiase结果图

可以看出，除偏后，图像的清晰度和对比度明显提高，噪点也明显减少。

5 结束语

基于传统的不动点迭代方法，文中提出了一种新的快速不动点迭代方法。该算法通过引入软阈值和正则化参数的双收缩，提高了算法的收敛速度和信号重构质量。通过在不同压缩比下比较各算法的重构性能，同时还比较了在相同压缩比下各算法的图像重构效果。仿真结果表明，所提的快速不动点算法较传统的不动点迭代方法性能更优。

[1]KashinBS,TemlyakovVN.Aremarkoncompressedsensing[J].MathematicalNotes,2007,82(5-6):748-755.

[2] 焦李成.自然计算、机器学习与图像理解前沿[M].西安:西安电子科技大学出版社,2008.

[3]CandesE,RombergJ.Quantitativerobustuncertaintyprinciplesandoptimallysparsedecompositions[J].FoundationsofComputeMathematics,2006,6(2):227-254.

[4]CandesE,RombergJ,TaoT.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.

[5]CandesE.Ridgelets:theoryandapplications[D].Stanford:StanfordUniversity,1998.

[6]DonohoDL,TsaigY.Extensionsofcompressedsensing[J].SignalProcessing,2006,86(3):533-548.

[7]TroppJA.Justrelax:convexprogrammingmethodsforidentifyingsparsesignalsinnoise[J].IEEETransactionsonInformationTheory,2006,52(3):1030-1051.

[8]WakinMB,LaskaJN,DuarteMF,etal.Anarchitectureforcompressiveimaging[C]//IEEEinternationalconferenceonimageprocessing.[s.l.]:IEEE,2006:1273-1276.

[9]WakinMB,LaskaJN,DuarteMF,etal.Compressiveimagingforvideorepresentationandcoding[C]//Proceedingsofthepicturecodingsymposium.Beijing,China:[s.n.],2006.

[10]LaskaJN,WakinMB,DuarteMF,etal.Anewcompressiveimagingcameraarchitectureusingoptical-domaincompression[C]//ProceedingsofSPIE.[s.l.]:[s.n.],2010:43-52.

[11]LustigM,DonohoD,PaulyJM.SparseMRI:theapplicationofcompressedsensingforrapidMRimaging[J].MagneticResonanceinMedicine,2007,58(6):1182-1195.

[12]TroppJA,WakinMB,DuarteMF,etal.Randomfiltersforcompressivesamplingandreconstruction[C]//IEEEinternationalconferenceonacoustics,speechandsignalprocessing.[s.l.]:IEEE,2006:14-19.

[13]KirolosS,LaskaJ,WakinM,etal.Analog-to-informationconversionviarandomdemodulation[C]//IEEEDallas/CASworkshopondesign,applications,integrationandsoftware.[s.l.]:IEEE,2006:71-74.

[14]LaskaJ,KirolosS,MassoudY,etal.Randomsamplingforanalog-to-informationconversionofwidebandsignals[C]//IEEEDallas/CASworkshopondesign,applications,integrationandsoftware.[s.l.]:IEEE,2006:119-122.

[15]LaskaJN,KirolosS,DuarteMF,etal.Theoryandimplementationofananalog-to-informationconverterusingrandomdemodulation[C]//IEEEinternationalsymposiumoncircuitsandsystems.[s.l.]:IEEE,2007:1959-1962.

[16]YangJ,ZhangY,YinW.AfastalternatingdirectionmethodforTVL1-L2signalreconstructionfrompartialFourierdata[J].IEEEJournalofSelectedTopicsinSignalProcessing,2010,4(2):288-297.

[17] 刘晓曼,丛 佳,朱永贵.不动点方法及其在压缩感知核磁共振成像中的应用[J].中国传媒大学学报:自然科学版,2014,21(1):28-34.

[18] 段世芳,马社祥.图像压缩感知的双收缩快速迭代算法[J].计算机工程,2012,38(19):226-228.

[19]HaleET,YinW,ZhangY.Afixed-pointcontinuationmethodfor'1-regularizedminimizationwithapplicationstocompressedsensing[R].[s.l.]:[s.n.],2007.

Research on Iteration Algorithm Based on a Fast Fixed Point in Compressed Sensing

LIU Yan,SONG Huan-huan,LI Lei

(Unstructured Data Calculation Theory and Application Research Center,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

Due to the low convergence rate of traditional iterative methods for solving large-scale problems,a fast fixed point continuation method is proposed after introducing the reconstructed models and the traditional fixed point continuation methods.This method,which brings in soft threshold shrinkage and regularization parameter shrinkage,restores image signals by gradual iteration in order to speed up the convergence rate and improve the quality of restored images.Simulation results show that compared with traditional fixed point continuation methods,it makes Peak Signal to Noise Ratio (PSNR) of the reconstructed image higher and the relative error smaller,and reduces running time when the sampling rate is low.

Compressed Sensing (CS);image reconstruction;fixed point continuation method;fast fixed point continuation method;convergence speed;quality of reconstructed

2016-04-21

2016-08-11

时间：2017-02-17

国家自然科学基金资助项目(61070234,61071167,61373137,61501251);江苏省普通高校研究生科研创新计划资助项目(KYZZ15_0236)；南京邮电大学引进人才科研启动基金资助项目(214191)

刘 艳(1991-)，女，硕士，研究方向为非线性分析及其应用；李 雷，教授，研究方向为智能信号处理和非线性科学及其在通信中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20170217.1628.028.html

TP301.6

A

1673-629X(2017)03-0052-05

10.3969/j.issn.1673-629X.2017.03.011