一种基于LDPC码译码的改进型最小和译码算法及仿真

焦冬莉，谭艳丽，赵永强，薄晓宁

(太原工业学院电子工程系，山西 太原 030008)

一种基于LDPC码译码的改进型最小和译码算法及仿真

焦冬莉，谭艳丽，赵永强，薄晓宁

(太原工业学院电子工程系，山西 太原 030008)

基于LDPC码译码原理提出了一种新的高效的最小和译码算法。对基于双曲正切规则的校验节点更新过程中的两个方向的处理进行了简化。出于减少水平处理过程中近似误差的考虑，新算法降低了复杂度。垂直方向的部分与和积译码算法相同，另一部分采用MS算法简化了计算。与严格的逼近方法相比，该方法具有计算复杂度低的优点。仿真结果表明,新提出的算法可以非常接近传统译码算法的性能。

计算复杂度；MS算法；仿真

LDPC(Low Density Parity Check)码是一种基于稀疏奇偶校验矩阵编码的分组码，是哥拉格(Gallager)[1]于1962年发现的。然而，由于当时计算机处理能力的限制和相关理论的薄弱，因此并未受到人们的足够重视。随着上世纪90年代Turbo码的兴起，人们认识到LDPC码也是一种较好的编码。1996年，MacKay从现代编码理论观点出发，重新研究LDPC码，获得了巨大的突破[2]。LDPC码凭借其优异性能及其在信息可靠传输中的良好应用前景[3](例如光通信，卫星通信、深空通信、第4代移动通信系统，高速与甚高速率数字用户线)，已引起世界各国学术界和IT业界的高度重视。

和积译码(简称SPA)算法是LDPC码中最流行的译码算法之一，又称为置信度传播算法[4]。从该算法名称就可以看出其保留了大量的加法、乘法数学运算，这大大限制了该算法的应用。人们基于此算法又提出了许多改进算法以降低算法的运算复杂度[5]，使其硬件实现更加容易。最小和译码算法是一种最突出的和积译码算法的次优算法[6]；迭代译码过程中的校验节点更新过程被大大简化，但性能也得到了损失。本文基于最小和译码的简化思路，提出一种新的校验节点更新过程，在保留迭代译码过程所需的主要外信息的基础上，使其运算量更接近于最小和译码算法。采用线性逼近的思路[7]，本文提出了一种新的改进方案简化对数函数的计算。最终提出的改进算法在与最小和译码算法有相似运算复杂度的情况下，性能得到了较大提高。

本文内容安排如下：第1部分简述最小和译码算法；第2部分给出了改进的算法方案，第3部分进行仿真结果分析，第4部分给出结论分析。

1 最小和译码算法

标准的LDPC码译码最小和算法(MS Algorithm)是并行迭代的软译码算法。消息传递的过程顺序与SP算法一样，但是更新的法则具有较大不同。MS 算法的译码公式如下：

初始化：对于每一个n∈{0,1,2,…,N}

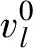
(1)

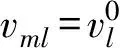
(2)

uml=0 .

(3)

迭代：1) 水平扫描(校验节点更新规则)

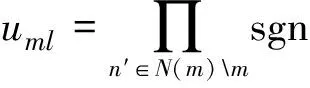
(4)

2) 垂直扫描(变量节点更新规则)

(5)

3) 译码：对每一个比特，计算其后验对数似然比(LLR)

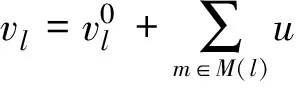
(6)

2 改进的算法方案

本部分主要集中于简化水平扫描过程既校验节点的更新，降低算法运算复杂度，使硬件实现变得更加容易。由经典的LLR-BP译码算法知道，校验节点的更新过程可以表示如下：

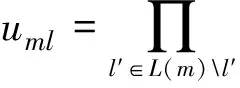
(7)

其中

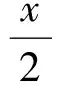
(8)

且

αml=sign(vml) .

(9)

对公式7中的核心函数f(x)做如下变换：

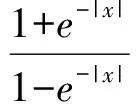
=log(1+e-|x|)-log(1-e-|x|)

≈a(x)-s(x) .

(10)

在式(10)中，用两条分段线性函数来逼近函数f(x)。对于去除了对数和指数的校验节点更新过程，运算量得到了较大的优化。函数a(x)能够被极其精确的用分段线性函数逼近，线性函数的斜率为以2为底的指数次幂。图1中的曲线表示分段逼近

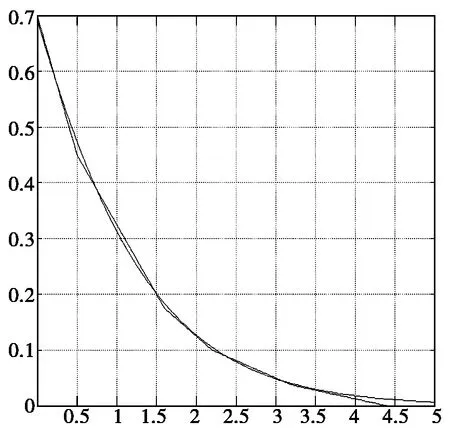
图1 函数a(x)=log(1+e-|x|)

函数与标准函数的接近程度，表1是分段逼近函数在各个区间上的具体表现形式。

表1 函数log(1+exp(-x))的分段线性逼近函数

函数S(x)能够极其精确的用分段线性函数逼近，其均方误差小于0.05。图2是分段逼近函数与标准函数的接近程度，表2是分段逼近函数在各个区间上的具体表现形式。

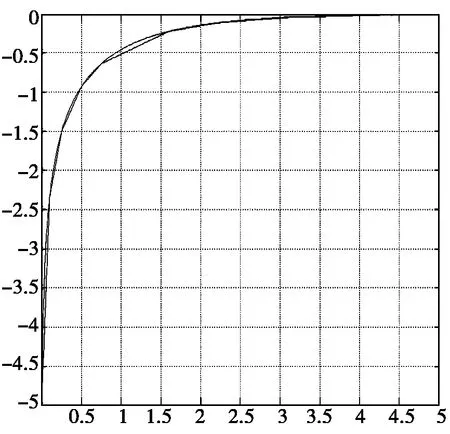
图2 函数s(x)=log(1-e-|x|)

由最小和译码算法的思想，对经典的SPA译码算法进行一种新的处理方式。随机的保留一半数量的水平方向的校验节点外信息，在一定的误差范围内降低水平方向更新过程的计算量。式11是经典LLR-BP算法的水平方向更新过程。

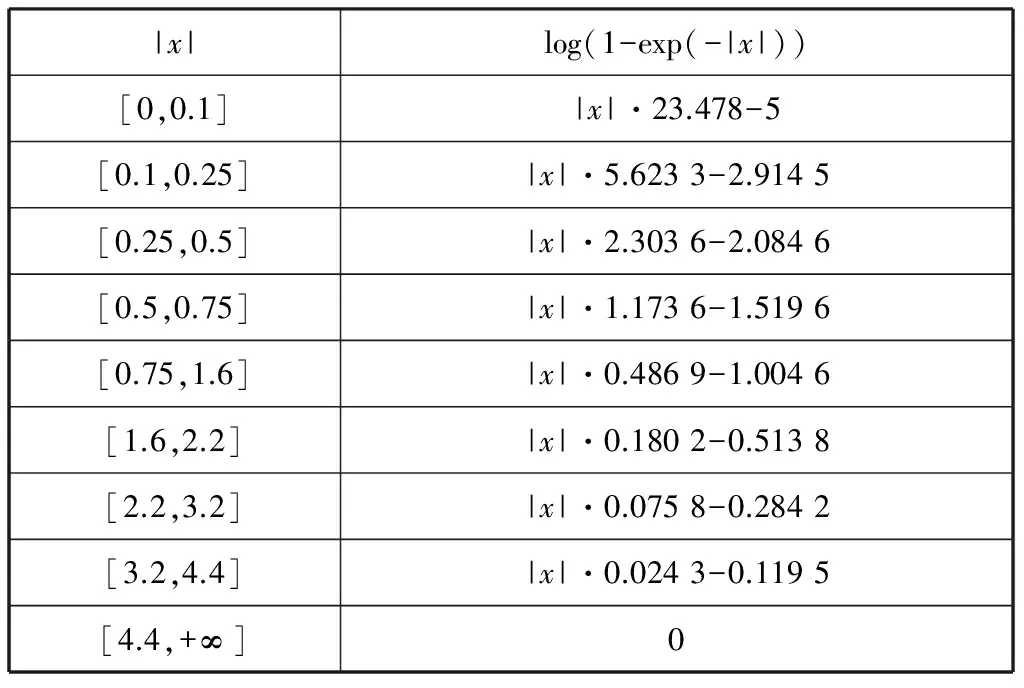
表2 函数log(1-exp(-x))的分段线性逼近函数

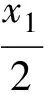
(11)

对式(11)进行如下操作，变化为式(12)或(13)

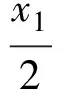
(12)

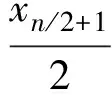
(13)

在水平方向的更新过程中，选择式(12)或者(13)作为水平方向的数据处理依据。

3 仿真及仿真结果分析

图3、4分别是BPSK调制下，使用1/2、2/3、3/4、5/6码率码长为576和2304时的三种不同译码算法的误码率曲线图。仿真的实验环境为高斯信道，所使用的迭代次数都是30次。

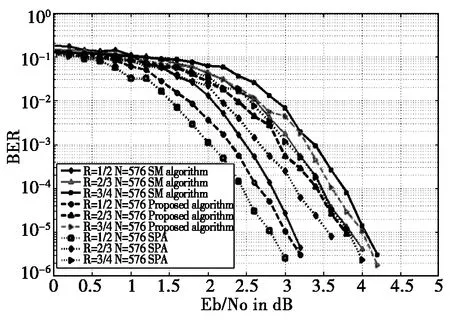
图3 L=2304，迭代次数为30时性能曲线

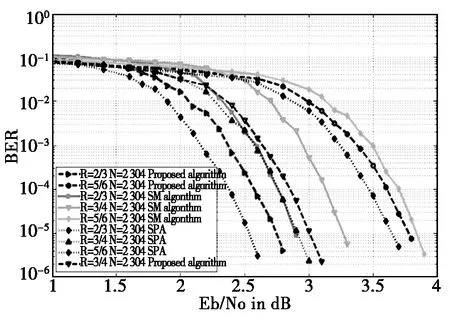
图4 L=2304，迭代次数为30性能曲线

从图3、4中可以看出，无论是哪种码率或者码长，SPA算法都具有最好的译码性能，改进的算法紧随其后，而最小和译码算法的性能最差，说明无论在何种情况下，改进的算法都在运算复杂度和译码性能上取得了一个很好的折中。从图3中可以看出，改进算法相较于最小和译码算法性能最大提升0.3 dB。从图4中可以看出，改进算法在低码率低信噪比情况下，性能提升情况更加明显。

表3描述了在校验节点更新过程中的主要运算量。我们知道在LDPC码的迭代译码过程中，大量的数据运算主要集中于校验节点更新。在改进算法中，整个运算过程中已经不再包含特殊运算，并且加法和乘法等常规的运算次数也有了大幅度的降低。相较于最小和译码算法，改进算法的运算随着节点数量的增多都是呈线性增长。

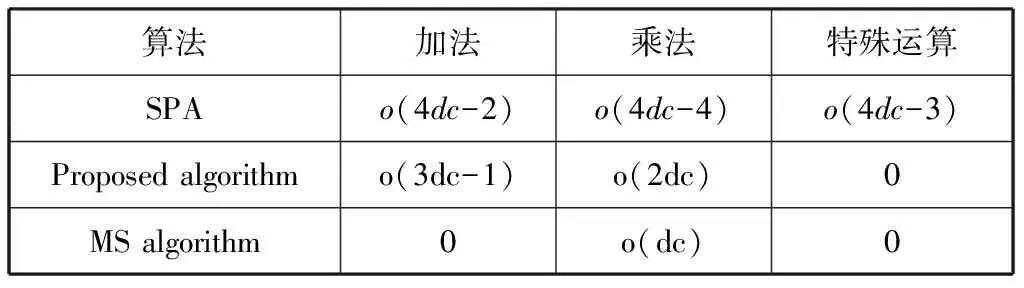
表3 各种算法的运算量对比

注：dc是奇偶校验矩阵的行重

4 结论

本文提出了一种新的改进的关于LDPC码的迭代译码算法。对基于双曲正切函数的水平更新过程，本算法得到了较大优化。在降低算法运算量的基础上，并没有降低译码性能。而基于最小和译码思路的简化过程，在减少运算量的同时也使得性能优于最小和译码算法。因此改进的译码算法是一个完全可行的，并且优于最小和译码算法的译码算法。

[1] Gallager R G.“Low-density Parity-check Codes,” IRE Trans[J].Inform Theory,1968，IT-8：21-28.

[2] MacKay J C.Good Error-correcting Codes Based on Very Sparse Matrices[J].IEEE Trans Inf Theory,1999,45：399-431.

[3] Chung S Y,Forney G D,Jr., T J.Richardson,et al.On the Design of Low-density Parity-check Codes Within 0.004 5 dB of the Shannon Limit[J].IEEE Commun Lett,2001,5:58-60.

[4] Richardson T,Urbanke R.The Capacity of Low-density Paritycheck Codes Under Message-passing Decoding[J].IEEE Trans Information Theory,2001,47(2):599-618.

[5] Chen J,Dholakia A,Eleftheriou E,et al.Reduced Complexity Decoding of LDPC Codes[J].IEEE Trans Commun,USA,2005,53(8):1288-1299.

[6] Wiberg N,Loeliger H A,Koetter R.Codes and Iterative Decoding on General Graphs[J].Eur Trans Telecommun,1995(6):513-526.

[7] Papaharalabos S,Sweeney P,Evans B G,et al.Performance Evaluation of a Modified Sum-product Decoding Algorithm for LDPC Codes[G].Proc.2nd Int. Symp. Wireless Commun.Systems (ISWCS),Siena,Italy,September,2005:800-804.

A Novel Modified MS Algorithm Based on LDPC Code Decoder

Jiao Dongli, Tan Yanli, Zhao Yongqiang, Bo Xiaoning

(TaiyuanInstituteofTechnology,TaiyuanShanxi030008,China)

A novel efficient Min-sum (MS) algorithm with LPDC code is proposed in this paper. Basing on the hyperbolic tangent rule, the check node update with two horizontal processes is modified with similar calculation. The proposed algorithm reduces the complexity, which is motivated by reducing the approximation error in the horizontal process. One part of the vertical process is the same with sum-product algorithm (SPA), and the other part adopts MS algorithm and simplifies the calculation. Compared with the exiting approximations, the proposed method has low computational complexity than SP algorithm. The simulation results show that the performance of this algorithm is very close to the general algorithm.

calculation complexity; MS algorithm; simulation

2016-11-10

焦冬莉(1971- )，女，山西运城人，讲师，研究方向：信号分析与处理。

1674- 4578(2017)01- 0022- 04

TP301.6

A