数学思想方法在化学中的应用

江苏 印志林

(作者单位：江苏省常州市横山桥高级中学)

数学思想方法在化学中的应用

作为一门工具学科，数学在化学的各个领域中都有着广泛的应用。在化学复习中重视数学思想方法的运用，有意识地将化学问题抽象为数学问题，可提高自己的思维能力和复习效率。下面具体举例，就数学思想方法在化学中的应用进行分析。

一、基础数学知识的运用

数学知识在化学中的运用几乎是无处不在的。例如，用数轴表示溶液的pH或化学反应的产物，用几何知识判断有机物分子中原子的位置关系，用集合图表示化学概念之间的逻辑关系，用数学归纳法归纳核外电子的排布规律或某类有机物的分子通式，用排列组合知识判断同分异构体的数目，用不等式求数值范围，等等。学习时要有数学意识，自觉地建立数学模型，借用数学知识分析解决化学问题。

例1 研究反应物的化学计量数与产物之间的关系时，使用类似数轴的方法可以收到的直观形象的效果。下列表达不正确的是

( )

A．密闭容器中CuO和C高温反应的气体产物：

B．Fe在Cl2中的燃烧产物：

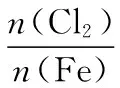
C．AlCl3溶液中滴加NaOH后铝的存在形式：

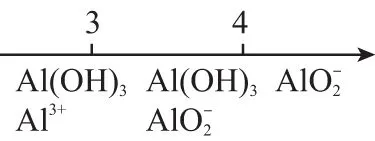
D．氨水与SO2反应后溶液中的铵盐：

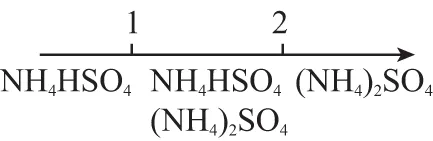
解析：A、C、D项中反应的产物与反应物的物质的量之比有关；Fe在Cl2中燃烧的产物只有FeCl3，与Fe和Cl2的用量无关。

答案：B

( )

A．5___________ B．7___________ C．8___________ D．10

答案：D

二、基本数学思想的运用

数学思想是对数学事实与理论经过概括后产生的本质认识，掌握数学思想，就是掌握数学的精髓。将数学思想应用于化学学科，是化学学科趋于成熟的一大表现。

1．数形结合思想

化学中形式多样的图象问题，就是数形结合的具体体现。不管是哪类图象题，解题的关键都是要看懂图象，分析曲线的坐标、起点、转折点、平台、终点及变化趋势所表示的含义，联系有关知识规律解决问题。

例3 25℃时，取浓度均为0.1 mol·L-1的醋酸溶液和氨水各20 mL，分别用0.1 mol·L-1NaOH溶液、0.1 mol·L-1盐酸进行中和滴定，滴定过程中pH随滴加溶液的体积变化关系如图所示。下列说法正确的是

( )

A．曲线Ⅰ：滴加溶液到10 mL时,

c(CH3COO-)>c(Na+)>c(H+)>c(OH-)

B．曲线Ⅰ：滴加溶液到20 mL时，

C．曲线Ⅱ：滴加溶液在10 mL～20 mL之间,

D．曲线Ⅱ：滴加溶液到10 mL时,

c(CH3COO-)-c(CH3COOH)=2[c(H+)-c(OH-)]

答案：D

2．方程函数思想

方程函数思想在化学计算中的使用非常普遍。有关混合物的计算是高中化学中常见的题型，其解题过程大体可分为两个阶段，第一阶段利用化学知识找出题目中各物质或量的关系，第二阶段利用关系列出方程计算得出结果。

例4 1.52 g铜镁合金完全溶解于50 mL密度为1.40 g/mL、质量分数为63%的浓硝酸中，得到NO2和N2O4的混合气体1 120 mL (标况)，向反应后的溶液中加入1.0 mol/L NaOH溶液，当金属离子全部沉淀时，得到 2.54 g 沉淀，下列说法不正确的是

( )

A．该合金中铜与镁的物质的量之比是2∶1

B．该浓硝酸中HNO3的物质的量浓度是14.0 mol/L

C．NO2和N2O4的混合气体中，NO2的体积分数是80%

D．得到2.54沉淀时，加入NaOH溶液的体积是600 mL

答案：D

另外，分类讨论、等价转化、分类与整合、化归与转化、特殊与一般等数学思想在化学中也都有重要应用，同学们可以在做题过程中自己去体会。

三、重要数学方法的运用

在化学计算中，有几种常用的特殊数学方法，运用这些方法解题，往往可以出奇制胜。

1．差量法

差量法是指根据化学反应前后物质的量发生的变化，找出“理论差量”。这种差量可以是质量、物质的量、气态物质的体积和压强、反应过程中的热量等。用差量法解题时，应先把化学方程式中的对应差量(理论差量)跟差量(实际差量)列成比例，然后求解。

例5 为了检验某含有NaHCO3杂质的Na2CO3样品的纯度，现将w1g样品加热，其质量变为w2g，则该样品的纯度(质量分数)是

( )

解析：样品受热时NaHCO3分解，根据固体质量变化可列质量差比例求解。

168___________ 106___________62

m(NaHCO3)___________(w1-w2) g

答案：A

2．平均值法

若混合物只有A、B两种成分，且已知M1>M2，则必有M1>M>M2[M代表平均相对原子(分子)质量、平均浓度、平均含量、平均生成量、平均消耗量等]。若已知M，则M1和M2必有一个比M大，另一个比M小。也就是说我们只要知道M就可推知M1、M2的取值范围，而不需要进行复杂的计算就可以迅速得出正确的答案。

例6 将15 g由两种金属组成的混合物投入足量盐酸中，充分反应后得到11.2 L H2(标准状况)，则原混合物的组成肯定不可能为

( )

A.Mg和Ag________________B.Zn和Cu

C.Al和Zn___________D.Al和Cu

解析：本题可用平均摩尔电子质量(即提供1 mol电子所需的质量)法求解。反应中H+被还原生成H2，产生0.5 mol H2需得到1 mol e-，即15 g 金属混合物可提供1 mol e-，其平均摩尔电子质量为15 g·mol-1。各选项中，金属Mg、Zn、Al的摩尔电子质量分别为12 g·mol-1、32.5 g·mol-1、9 g·mol-1，其中不能与盐酸反应的Ag和Cu的摩尔电子质量可看作无穷大。根据平均值原理可知，原混合物中一种金属的摩尔电子质量大于15 g·mol-1，另一金属的摩尔电子质量小于15 g·mol-1，据此可得答案。

答案：B

3．极值法

极值法是采用极限思维方式解决一些模糊问题的解题技巧。它是将题设构造为问题的两个极端，然后依据有关化学知识确定所需反应物或生成物的量值，进行判断分析，求得结果。

( )

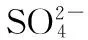
A.9.0 L___________B.13.5 L

C.15.7 L___________D.16.8 L

解析：12.0 g CuO 的物质的量为0.15 mol。混合气体中，NO2和NO的体积比为1∶1，则其组成相当于NO1.5，N的平均化合价为+3价。

①若混合物中只有CuS，则CuS的物质的量为0.15 mol。

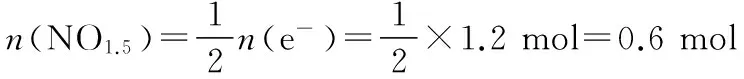
②若混合物中只有Cu2S，则Cu2S的物质的量为0.075 mol。

因此，V的取值范围为8.4

答案：A

(作者单位：江苏省常州市横山桥高级中学)

趣味阅读

诺贝尔化学奖趣闻(一)

获奖人数——自1901年设立以来至2013年，诺贝尔化学奖一共颁发了105次。在112年的历史上，共有166人次获颁诺贝尔化学奖。不过，由于英国生物化学家弗雷德里克·桑格曾在1958年及1980年两度问鼎，实际获奖人数应该是165。从1901年到2013年，独享诺贝尔化学奖荣耀的科学家共有63位；由两位获奖者平分秋色的情况出现过23次；另有19次为三个人分享大奖，今年便是如此。

最年轻的获奖者——1935年，35岁的法国科学家弗雷德里克·约里奥捧得诺贝尔化学奖桂冠，成为该奖项最年轻的获奖者，与他携手走上领奖台的还有他的妻子伊雷娜·约里奥·居里(居里夫人的长女)。

8次空缺——诺贝尔化学奖的颁发出现过8次空缺：1916年、1917年、1919年、1924年、1933年、1940年、1941年和1942。原因不外乎两点：没有能够达到评奖标准的候选者，以及众所周知的不可抗力——一战和二战。