基于改进混杂扩展卡尔曼滤波的炮弹阻力系数辨识

杨 靖,常思江,王中原

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

基于改进混杂扩展卡尔曼滤波的炮弹阻力系数辨识

杨 靖,常思江,王中原

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

针对利用炮弹飞行数据辨识阻力系数的问题,提出了一种改进形式的混杂扩展卡尔曼滤波(IHEKF)方法。引入虚拟过程噪声并且在每个时间步长对称化协方差矩阵,避免了混杂扩展卡尔曼滤波在实际应用中由于系统建模误差及弹载计算机的精度有限引起的发散问题,提高了阻力系数辨识的鲁棒性。数值仿真结果表明:当建模误差可以忽略不计时,采用IHEKF能以高精度辨识出阻力系数;当建模误差较大时,采用IHEKF具有较好的鲁棒性。

炮弹;无控飞行;参数辨识;扩展卡尔曼滤波

火炮武器系统在战场中反应迅速,能够提供强大且持续的火力支援,是未来部队联合作战的重要组成单元。随着现代战争理念的发展,远程压制、精确打击及高效毁伤等成为适配弹箭的发展方向。受炮射平台的限制,新型适配的弹箭往往修正能力或控制能力有限。因此,提高参数的准确度,降低模型误差,对充分发挥新型弹箭的潜在能力具有重要意义。

气动参数的获得方法分为三大类[1]:计算流体力学方法,风洞吹风法,利用飞行数据进行参数辨识的方法。数值计算得到的结果可作为参数的先验知识,风洞试验与飞行试验可用来校正参数。3种方法相辅相成,可以获得更为准确的气动参数。本文研究在已获得先验气动参数的基础上,利用飞行试验数据辨识弹箭阻力系数的问题。

关于利用飞行试验数据提取弹箭阻力系数的问题,许多学者开展了研究。祁载康[2]采用多段样条曲线拟合的方式,设计了一种通过雷达遥测数据提取弹丸阻力系数的方法。杜昌平等[3]提出了一种基于遗传算法的分段多项式拟合阻力系数辨识方法。Dutta等[4]采用最大似然估计理论,设计了一种阻力系数的辨识方法。Rogers等[5]针对智能弹药,提出了一种基于证据理论的参数估计方法。史金光等[6]将阻力系数辨识问题转化为状态估计问题,应用扩展卡尔曼滤波方法,通过地面雷达测量的数据对弹道修正弹进行了阻力系数辨识。相比于多项式拟合及最大似然估计等离线辨识方法,将参数辨识问题转化为状态估计问题,可以实现在线递归估计。对于某些应用问题,实时的参数辨识具有重要意义。因此,本文将阻力系数的辨识问题转化为状态估计问题。

阻力系数辨识需要的弹道信息可采用北斗二代接收机获得。北斗导航系统是我国具有完全自主知识产权的全球导航定位系统,可以提供三维位置和速度信息,其采用载波相位测量原理的二代产品可实现厘米级的定位精度[7]。

实际中,描述弹箭运动轨迹的弹道模型是连续时间的,而采用的测量数据往往是离散的。采用扩展卡尔曼滤波需要对弹道模型进行离散化处理,而混杂扩展卡尔曼滤波方法(HEKF)[8]可直接应用于这种情形。但是,弹道建模与实际的弹箭飞行过程总是存在一定的偏差,且弹载计算机的精度有限,存在截断误差,直接应用标准形式的HEKF可能出现状态估计发散的问题。

基于上述考虑,本文将利用北斗测量数据辨识炮弹阻力系数的问题转化为状态估计问题。引入虚拟过程噪声并且在每个时间步长对称化协方差矩阵,增强混杂扩展卡尔曼滤波方法的鲁棒性和状态估计精度。应用改进的方法进行阻力系数辨识。

1 问题描述

采用北-天-东地面坐标系作为参考惯性坐标系,记为OxEyEzE。由外弹道理论[9]可知,六自由度刚体弹道模型可以较为全面地描述弹箭飞行过程的运动特征。但是,该模型较为复杂,系统阶数较高,包含较多参数以及不可测量的状态信息,不便于直接用于参数辨识。因此,将六自由度弹道模型作为基准弹道,而辨识过程采用下述简化模型。

为得到合理的简化模型,采用分层思想,在高度方向对弹道进行分层,如图1所示,在每一层内,炮弹的高度与速度变化不大,从而随高度变化的空气密度以及随弹体质心与气流相对速度变化的阻力系数可近似为常数。若炮弹具有较好的动态稳定性,则在每一弹道层内其绕心运动对质心运动造成的影响相对较小。因此,可以用质点弹道模型近似描述在每一弹道层内的弹体运动过程。

图1 弹道分层示意图

取系统状态为

x=(xyzvxvyvz)T

(1)式中:x,y,z分别为弹体质心位置分量;vx,vy,vz分别为弹体质心速度在地面坐标系OxEyEzE中三轴的分量。

假设当地风速为常值,将随机风及其他随机因素对炮弹运动的作用描述为高斯白噪声,即ω～N(0,Q),可得随机质点弹道模型:

(2)

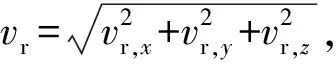
综上所述,阻力系数辨识问题描述为采用式(2)的随机质点弹道模型,利用每一弹道层的飞行数据(位置与速度测量值),获取对应的阻力符合系数kD。

2 改进的混杂扩展卡尔曼滤波器

随机质点弹道模型(2)是连续时间的,而采用的测量数据往往是离散的。混杂卡尔曼滤波方法(HEKF)适用于这种情形的状态估计问题。然而,在实际应用中,由于弹载计算机的精度有限以及建模误差等因素,标准的HEKF可能会出现发散问题。因此,本文在标准HEKF的基础上引入2种改进策略,得到了一种实用的改进形式的HEKF。

2.1 标准形式的HEKF

考虑状态方程由微分方程描述而量测方程是离散的一般形式的动力学系统:

(3)

式中:状态向量x∈Rn,输出向量y∈Rm,向量yk为输出向量y的第k次测量值,向量xk为对应采样时刻的系统状态,ω∈Rn为系统过程噪声,vk∈Rm为量测噪声,将ω及vk假设为高斯白噪声,则

(4)

时间更新方程表示为

(5)

(6)

量测更新方程表示为

(7)

(8)

2.2 改进策略

时间更新方程(5)中的第二式等价于量测协方差矩阵趋于无穷的微分Riccati方程,要求协方差矩阵P始终为对称矩阵。然而,数值求解该微分方程时,由于计算机精度有限,存在舍入误差。因此,在时间更新过程中的每一次积分后,对称化协方差矩阵P,即令

P=(P+PT)/2

(9)

为后续表述方便,将采用上述改进策略的标准HEKF记为IHEKF。

3 基于IHEKF的阻力系数辨识

采用滤波方法进行参数辨识的思想是将未知常值参数增广为系统状态,利用滤波方法对增广后的系统进行状态估计,从而获得待辨识的未知常值参数。本节以式(2)描述的随机质点模型为基础,将阻力符合系数kD扩展为系统状态,得到用于阻力系数辨识的增广随机质点模型。然后,利用IHEKF对所得到的增广模型进行状态估计,即实现了阻力系数的辨识。

3.1 用于阻力系数辨识的增广质点模型

将阻力系数增广为系统状态,可得:

xa=(xyzvxvyvzkD)T

(10)

结合式(2),可得新的随机质点弹道模型:

(11)

(12)

对照式(6),可得噪声增益矩阵为La=I7×7,I为单位矩阵,增广状态偏导数矩阵为

其中:

(13)

(14)

(15)

3.2 量测模型

北斗导航系统是我国具有完全自主知识产权的全球导航定位系统,可以提供三维位置和速度信息。因此,本文以北斗定位装置的测量信息进行阻力系数的辨识。

北斗导航系统采用东-北-天导航坐标系OxNyNzN。该坐标系与本文采用的地面坐标系OxEyEzE是相对静止的,其转换易于实现。因此,直接在地面坐标系下描述北斗二代系统的测量模型。

量测向量取为

yk=(xyzvxvyvz)T

(16)

量测方程可表示为

yk=Hkxa,k+Mkvk

(17)

式中:Hk=(I6×6O6×1),Mk=I6×6。

4 数值仿真分析

为验证本文提出的改进型混杂卡尔曼滤波器(IHEKF)在实际应用中的有效性与优越性,本节分2种情形进行了仿真分析:其一为IHEKF在无系统建模误差情况下的阻力系数辨识;其二为存在系统建模误差情况下的IHEKF与标准形式的HEKF的阻力系数辨识性能对比。

1)无系统建模误差(情形1)。

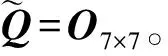
图2～图4展示了采用IHEKF在无系统建模误差情形下的滤波过程。可以看出,位置滤波误差Δx,Δy,Δz,速度滤波误差Δvx,Δvy,Δvz与阻力符合系数辨识误差ΔkD都很快趋于稳定。状态估计协方差矩阵很好地预测了滤波结果。表1给出了整个过程的各状态估计偏差的标准差S(·)。

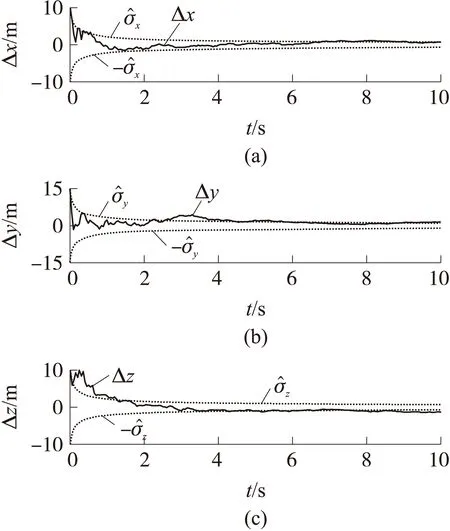
图2 IHEKF方法的位置滤波误差(情形1)

图3 IHEKF方法的速度滤波误差(情形1)

图4 IHEKF方法的阻力符合系数辨识误差(情形1)

表1 估计误差标准差

2)有系统建模误差(情形2)。

如前所述,六自由度刚体弹道模型可以较为全面地描述炮弹在空中的实际飞行过程。因此,本节将六自由度刚体弹道仿真数据作为实际的测量数据。显然,式(2)的随机质点弹道模型与六自由度刚体弹道模型相比存在一定的系统建模误差。

图5～图7为HEKF未引入过程噪声时的滤波过程。

图5 HEKF方法的位置滤波误差(情形2)

图6 HEKF方法的速度滤波误差(情形2)

图7 HEKF方法的阻力符合系数辨识误差(情形2)

由图可见,位置及速度滤波误差出现发散现象,尽管阻力符合系数的辨识结果收敛,但其收敛过程非常缓慢。状态估计协方差矩阵不再具有预测滤波结果准确度的性能。

图8～图10为引入过程噪声的IHEKF的滤波过程。

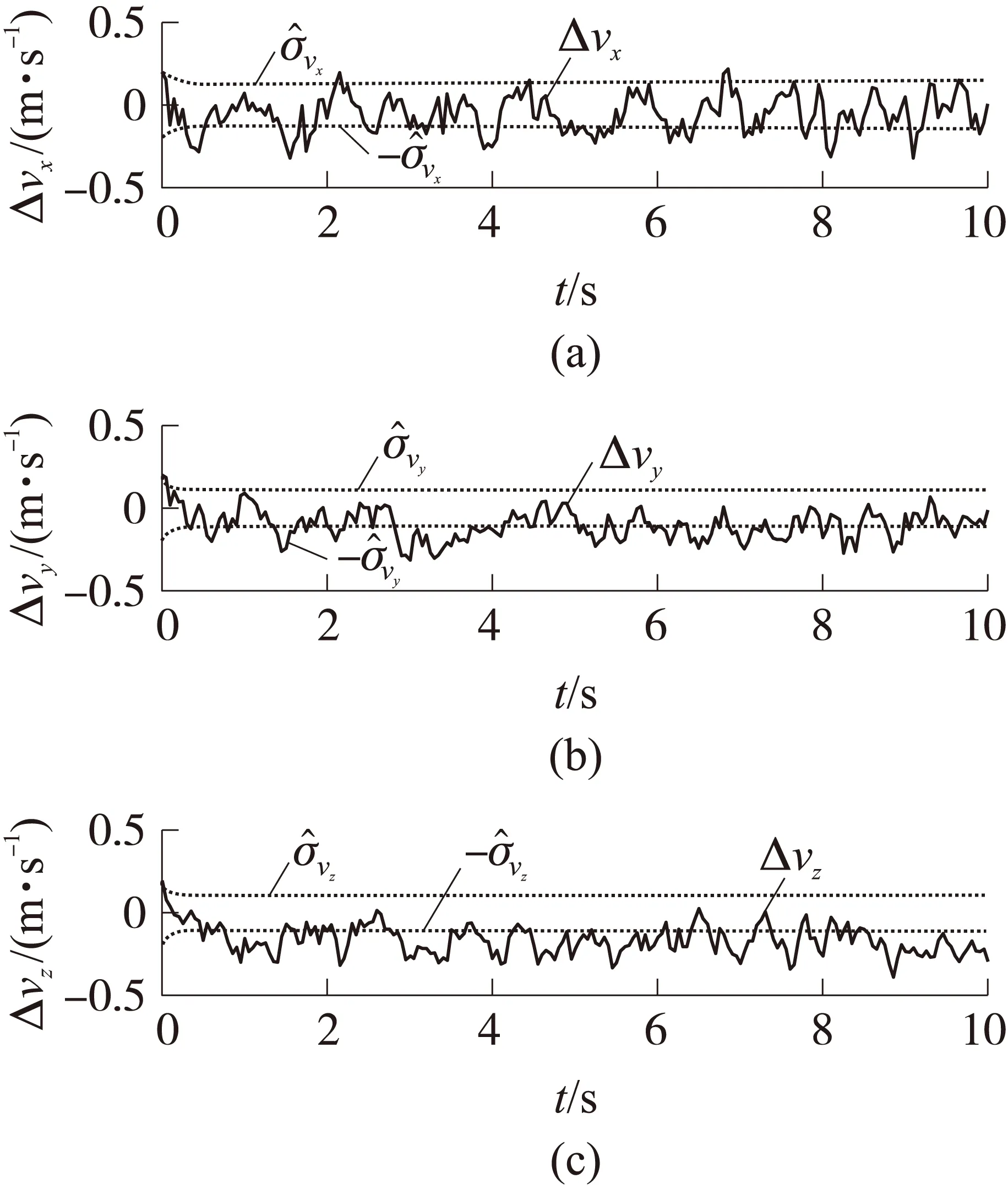
图9 IHEKF方法的速度滤波误差(情形2)

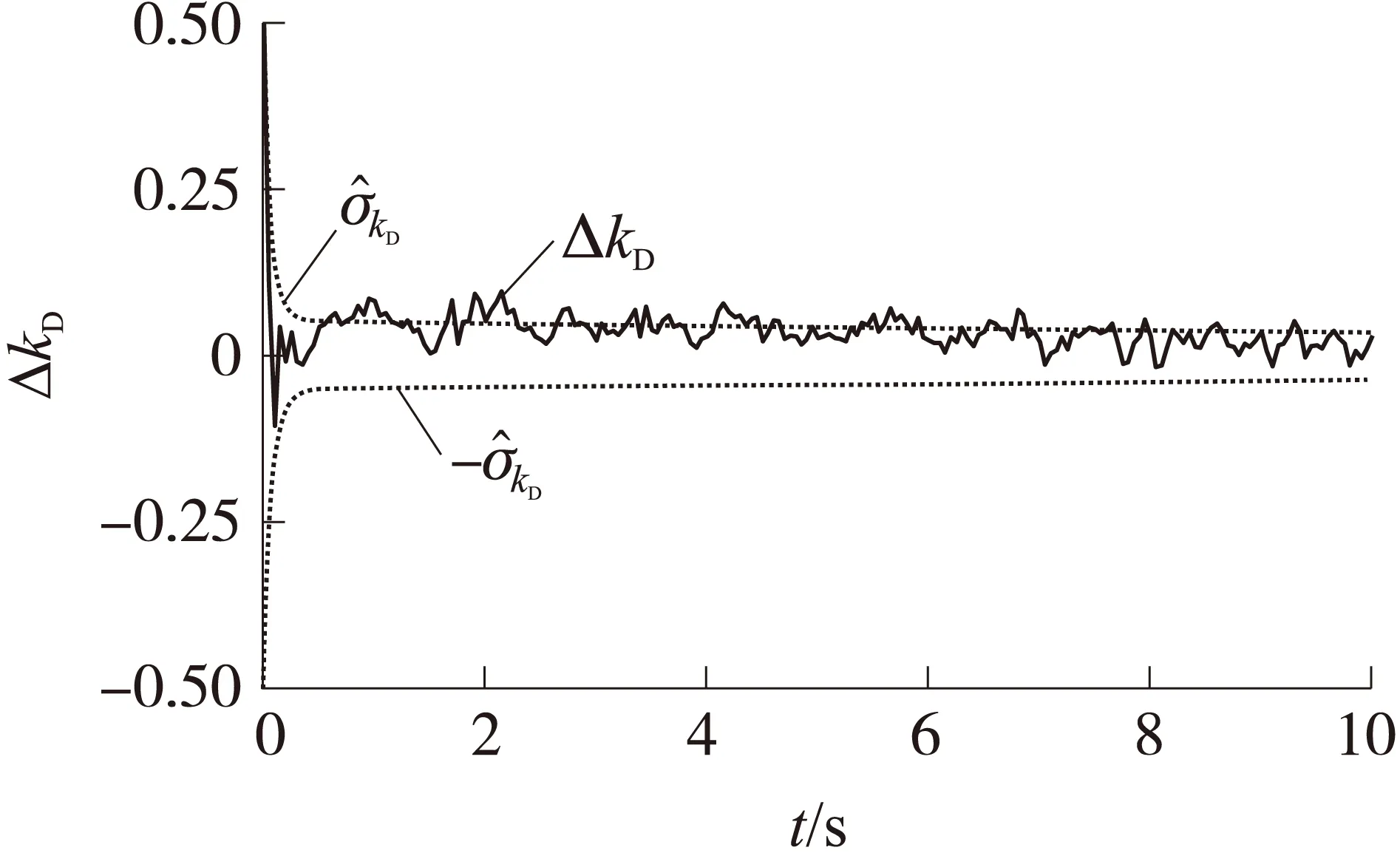
图10 IHEKF方法的阻力符合系数辨识误差(情形2)

可以看出,IHEKF方法在存在建模误差的情况下未出现滤波结果发散的现象。状态估计协方差矩阵对滤波结果具有较好的预测性。尽管阻力系数辨识的精度有所下降,但是提高了辨识过程的鲁棒性。

5 结束语

本文针对利用炮弹飞行数据辨识阻力系数的问题,提出了一种改进形式的混杂扩展卡尔曼滤波方法。在滤波过程中,引入虚拟过程噪声并且在每个时间步长对称化协方差矩阵。仿真结果表明:

①当建模误差可以忽略不计时,采用改进形式的混杂扩展卡尔曼滤波器能够以高精度辨识出阻力

系数;

②当建模误差较大时,采用改进形式的混杂扩展卡尔曼滤波器具有较好的鲁棒性。虚拟噪声过程的调整需要综合考虑实际应用中的炮弹飞行条件。

[1] KLEIN V,MORELLI E A.Aircraft system identification theory and practice[M].Reston:American Institute of Aeronautics and Astronautics,2006.

[2] QI Z.Multi-spline technique for the extraction of drag coefficients from radar data[J].Journal of Beijing Institute of Technology,1994(1):33-42.

[3] 杜昌平,周德云,宋笔锋,等.基于遗传算法的弹道参数辨识方法研究[J].西北工业大学学报,2008,26(3):373-376. DU Chang-ping,ZHOU De-yun,SONG Bi-feng,et al.Weapon parameter identification algorithm based on genetic algorithm[J].Journal of Northwestern Polytechnical University,2008,26(3):373-376.(in Chinese)

[4] DUTTA G G,SINGHAL A,GHOSH A K.Estimation of drag coefficient from flight data of a cargo shell:AIAA 2006-6149[R].Keystone:AIAA,2006.

[5] ROGERS J,COSTELLO M.Smart projectile state estimation using evidence theory:AIAA 2011-6337[R].Portland:AIAA,2011.

[6] 史金光,刘猛,曹成壮,等.弹道修正弹落点预报方法研究[J].弹道学报,2014,26(2):29-33. SHI Jin-guang,LIU Meng,CAO Cheng-zhuang,et al.Research on method of falling point prediction for trajectory correction projectile[J].Journal of Ballistics,2014,26(2):29-33.(in Chinese)

[7] 白征东,元荣,过静珺,等.北斗二代卫星厘米级相对定位[J].测绘通报,2014(7):11-13. BAI Zheng-dong,YUAN Rong,GUO Jing-jun,et al.Performing centimeter-level relative positioning using BeiDou navigation satellite system[J].Bulletin of Surveying and Mapping,2014(7):11-13.(in Chinese)

[8] SIMON D.Optimal state estimation:Kalman,H∞,and nonlinear approaches[M].New Jersey:John Wiley & Sons,Inc.,2006.

[9] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008. HAN Zi-peng.Exterior ballistics of projectiles and rockets[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

Drag Coefficient Estimation for Projectiles Based on Improved Hybrid Extended Kalman Filter

YANG Jing,CHANG Si-jiang,WANG Zhong-yuan

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

An improved hybrid extended Kalman filter(IHEKF)was proposed aiming at drag coefficient estimation from flight data of projectiles.The fictitious process noise was added to the system model,and the covariance matrix was symmetrized at each time-step.The divergence caused by modeling errors and finite precision of digital microprocessors onboard the projectiles in the implementation of HEKF is avoided,and the robustness is improved.While the modeling errors can be ignored,the IHEKF can estimate the drag-coefficient with high-precision;while the modeling errors are great,IHEKF has great robustness.

projectiles;free flight;parameter estimation;extended Kalman filter

2016-10-11

国家自然科学基金项目(11402117)

杨靖(1988- ),男,博士研究生,研究方向为弹箭飞行动力学,制导与控制。E-mail:JingYangNUST@163.com。

TJ303.4

A

1004-499X(2017)01-0028-06