非合作博弈下考虑用户满意度的虚拟电厂经济优化运行

路 尧，刘继春，许立雄

（四川大学电气信息学院，四川成都610065）

非合作博弈下考虑用户满意度的虚拟电厂经济优化运行

路 尧，刘继春，许立雄

（四川大学电气信息学院，四川成都610065）

现如今能源问题逐步受到重视，分布式发电（distributed generation，DG）以及网络通信技术的发展为更好地缓解能源需求紧张，改善环境问题，提高可再生能源渗透率等系列问题提供了可能。但到目前为止，传统的虚拟电厂（virtual power plant，VPP）优化研究更侧重于内部DG能量调配以及对外网提供市场交易等辅助服务方面，未能很好地考虑用户需求侧的负荷多样性和用电灵活性，以及其作为需求侧响应参与内部能源调配的主动性和互动性等突出问题。该文在此基础上，运用非合作博弈理论构建发电侧和用户需求侧的互动模型。此模型为解决提升发电侧与用户需求侧的互动灵活度等一系列问题提供了理论基础，并同时考虑用户满意度，以各自效用最大化为目标进行博弈寻优运算。仿真结果验证了所提理论的可行性，结果表明，此方法相比于VPP传统优化方案可实现兼顾用户满意度的用户负荷侧经济最优以及发电侧效用最优，并且有效地提高了可再生能源利用率，进而实现了VPP经济优化运行。

非合作博弈；虚拟电厂 （VPP）；用户满意度；经济优化

0 引言

随着世界人口增长和经济快速发展，能源紧缺越发成为公众关注的严峻问题，同时，被过分依赖的煤炭、石油等化石燃料的过度使用产生的大量碳排放也将给环境带来持续不断的不利影响［1－3］。鉴于此，分布式能源得到了广泛的应用，同时为平抑可再生能源［4］的随机性和波动性，在此引入虚拟电厂（virtual power plant，VPP）来有效聚合不同类型数量、地域结构的分布式电源（distributed generation，DG）以保证系统运行的稳定性和经济性［5－7］。

到目前为止，有关虚拟电厂的优化研究更倾向于诸如其内部DG的优化运行以及对外市场交易等方面。文献 ［8］通过包含有小型热电联产（combined heat and power，CHP）的VPP调度优化模型，考虑了在系统不同风险、储热容量的前提下，用户侧对激励信号的响应方式特点，以及对整个系统的出力运行描述。文献［9］研究了通过一种直接负荷控制（direct load control，DLC）的手段来进行对大量家用电器设备运行控制以及负荷管理，以实现VPP系统内部电量短缺的问题，从而更高效地从电力市场获取收益。不难发现，以上文献更侧重从系统单一电源侧或是负荷资源侧进行直接优化控制管理，或是直接对负荷侧资源“一视同仁”地统一化，简单传统地按照负荷是否具备可中断性进行归类划分。如文献［10-11］所示，用户负荷侧大量存在着可与系统进行互动的可平移负荷，而且就其相关用户用电情况以及转移度的不确定性进行了详述，但由于其过分强调用户侧经济性而造成其用电舒适度的牺牲。如今随着网络信息技术的完善和发展，在未来能源互联网［12］日新月异，不断发展、完善的大框架下，系统资源参与配置的开放性、自主性得到不断提高，凭借提升清洁能源等可再生能源渗透率来更好地平衡系统供需已然成为关注重点，另一方面，需求侧资源作为一种响应手段参与进来，同样作为参与系统综合资源调控的一方，用以配合发电侧资源，更好地平衡系统出力、资源调配以及获得经济最优。因此，基于以上分析，本文提出计及用户侧用电满意度的“发电-用户”两侧互动非合作博弈的VPP经济优化模型，通过对VPP内部能源出力的描述，令发电侧制定相关负荷激励措施，并与用户侧二者于非合作博弈条件下进行互动寻优。

1 VPP及其内部控制模型

1.1 VPP结构

VPP通过先进的通信控制技术将分布于相应区域内的不同类型以及不受地理位置限制的分布式能源有效整合起来，对外呈现为一个可操控的、类似于传统发电厂的柔性运行输出系统，而其内部的可再生能源发电诸如风机、光伏等本身具有出力随机性和间歇性特征，使得VPP具备对外开放型以及可与外部市场交易的特性［13］。本文所构建VPP结构模型如图1所示。

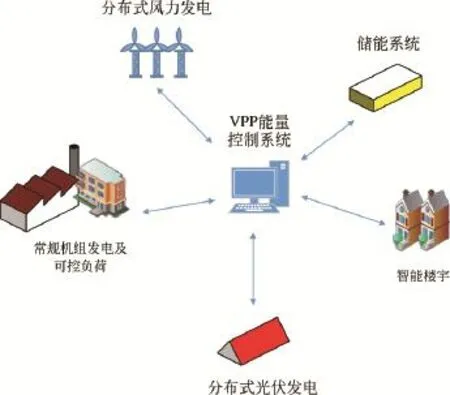
图1 VPP结构图Fig.1 Structure diagram of VPP

1.2 VPP运行控制方式

VPP内部控制策略通常有集中控制和分散控制方式。

首先是集中控制方式，其通过协调控制中心（control coordination centre，CCC）以双向通信通道对所辖范围内发电及用电单元进行自上而下的信息流交互和实时控制，具备强控制力和灵活多变的特点，但同时因通信流量巨大导致兼容性较差，为应对此问题，可在此控制模式下实施分层控制，即于特定批量的DG和用电单元处装设分布式电源控制器（distributed generation controller，DGC），从而对上层起到更好的信息分流和传达作用，有效地解决了扩展性差等问题。

不同于以上控制方式，完全分散控制则是将原本全权由控制中心负责调度管理的VPP分解为不同的智能自主性的子系统，其由相应智能代理管辖，原来的控制中心则“进化”为数据交换和处理中心。系统内部的信息交互和处理则是通过与子系统相对应的智能代理进行决策，并且需要多次的信息迭代进行更新和确定，但同时亦对此运行方式下子系统一系列复杂日常事务管理提出了高标准严要求。

1.3 风机模型

风速受气候、地形等因素影响进而产生随机性和不确定性，其概率密度函数可近似用Weibull分布函数进行描述，即

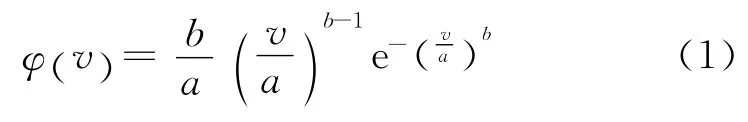
式中：v表示风速；a作为尺度参数，其大小受此时间段内风速数据的方差和均值影响；b为形状参数。并且由风速v可以得到其相应风机输出功率函数，即

式中：Pwind为风速vwind时的风机输出功率；vci，vco，vR分别为风机的切入、切出和额定风速；PR为该风机的额定出力。因此，风机出力就可用通过蒙特卡洛抽样得到的数据带入式（2）进行模拟计算。

1.4 光伏机组模型描述

光伏发电出力受当地光照强度等因素的影响，而光照强度数据则近似服从Beta分布函数，其系统出力数据亦如此。下面给出其相应概率密度函数，即

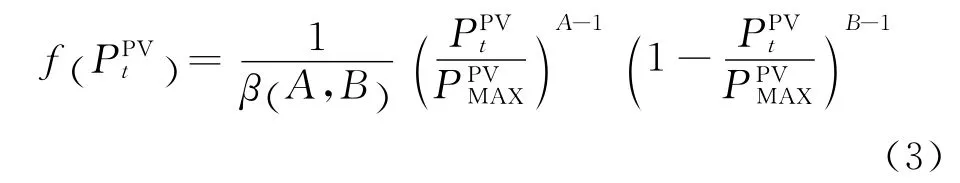
式中：PPVt表示某一时段的光伏出力；PPVMAX则表示其可能出力最大值；这里涉及Beta函数即β（A，B），其数学模型为

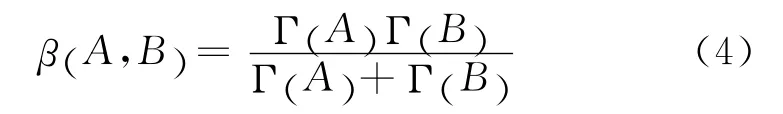
式中：A、B分别表示形状参数；Г（·）为Gamma函数。

式中：σPV、μPV分别表示光辐射强度的标准差和均值。

将气象预测数据及其相关参数带入式（3），并由其计算出光伏出力分布函数，再通过光伏出力函数即可得到所要模拟的光伏发电功率数据。

1.5 铅酸蓄电池组

蓄电池组的充放电状态与其荷电状态Qoc的关系为：

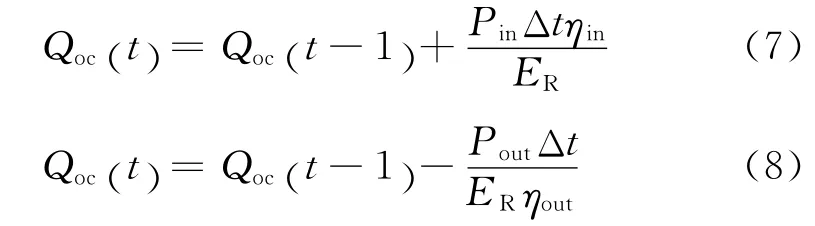
式中：Qoc、Pin、Pout、ηin、ηout、ER、Δt分别表示蓄电池组的荷电状态、充放电功率、充放电效率、蓄电池额定容量以及充放电时间。

1.6 柴油发电机组

式中：CG、PG，t分别代表柴油发电机组燃料成本、t时间段内机组净出力；aG、bG、cG分别表示发电机组成本系数。

2 考虑用户满意度的VPP经济调度模型分析

2.1 博弈论及VPP内部调度

博弈理论［14］主要用来描述各竞争主体之间为寻求利益而进行决策的互动关系。在一次博弈过程中，各参与者需根据其他参与者行为信息以及决策次序采取相应的策略，以获取自身收益。

根据博弈时各主体之间能否达成协议这个标准，又可分为合作博弈和非合作博弈。在非合作博弈中，还需考虑各博弈方信息是否透明，以及决策次序是否同步等变量，故而还可细分为（非）完全信息（静）动态博弈这4种博弈类型。

本文为分析考虑用户满意度条件下VPP经济调度系统中用户侧需求响应与VPP发电侧的互动关系，采用了非合作博弈理论中的完全信息动态博弈模型。旨在确保各决策主体于绝对理性条件下实现各自效用最大化，同时又能很好地促进可再生能源的消纳，提升了用户满意度。

2.2 VPP内部发电侧与用户侧互动博弈模型

互动博弈双方分别为发电侧与用户侧，其相应策略分别为电价和负荷，以全天划分为M＝24时段为例进行优化博弈。

构建用户侧使用负荷效用函数模型，其中包括购电成本以及用户用电满意度等部分，为实现用户效用最大化，则需对其成本函数模型取负；发电侧效用模型则可看作售电利润与用户满意度的差值，其中售电利润为售电收益与发电成本之差，其二者数学模型、发电侧发电成本模型及其相关参数模型如下：

式中：w1，w2分别代表发电侧与用户侧效用模型；si，ri，ci，gi分别表示i时段的售电电价，用户作为需求响应的实际用电量，发电侧发电边际成本以及相应发电量；Cj，OMj分别为第j类柴油机的燃油成本以及设备运行维护费；ξ为惩罚因子，代表可再生能源出力偏离总发电量的差值；γ为波动系数；gRE为i时段内可再生能源发电量；CR，yi（ri，ni）分别为用户成本以及用户用电满意度函数，其中ni为i时段用户侧需求电量，i＝1，2，…，M代表不同时段。

这里，用户满意度为用户需求电量与用户实际用电量二者构成的函数关系式，其具体反映二者偏差关系。不难看出，当需求电量低于实际使用电量时，用户满意度函数值为正，代表用户比较满意；而当需求电量高于用户实际用电量时，其值为负，此时用户不满意当前用电方式。其表达式如下：

式中：αi，βi表示t时段电价弹性参数以及与用户类型相关的参数，如图2所示。

图2 用户满意度在不同参数下函数曲线Fig.2 Users'satisfaction function curve for different values

决策双方在上述提及的效用函数模型条件下进行互动博弈时需满足以下约束。

（1）发电侧售电电价约束：

（2）用户实际用电量约束：

即保证当电价足够高时，不至于使用户实际用电量低于最小需求电量，即不可中断负荷电量；并且，也不会由于电价偏低造成用户用电量无上限，其值最大不应超过发电侧最大发电量和用户最大需求电量二者的最小值为宜，考虑到实际电力系统运行，则本文可令发电量近似为用户实际用电量，以方便计算。

（3）系统可中断负荷量约束：

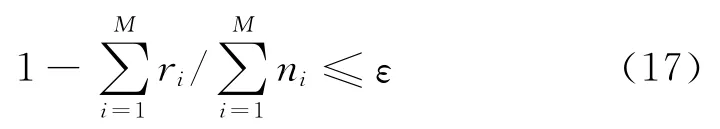
即表示可中断负荷存在比例限度值，式中ε表示可中断负荷最大存在比例。

（4）系统各分布式电源出力约束：

式中：Pj，i表示各分布式电源出力范围；Rj.max、Rj.min表示单位时间内各分布式电源出力的最大值与最小值。

（5）蓄电池充放电效率及剩余电量约束：

参照GB 17149-1-1997《化妆品皮肤病诊断标准及处理原则总则》斑贴试验方法进行试验，选取符合标准受试人员32人。将10种防晒剂溶液放入斑试器，取0.02～0.025 mL样品加在斑试器所附滤纸片上。

式中：Pbat，i，Ebat，0分别表示蓄电池i时段充放电功率以及初始零时刻荷电量；T为单位时间段，其中对储能电池单位时间充放电功率和相应剩余电量进行了约束；Qoc表示蓄电池荷电状态，为反映放电深度，其值应不小于0.35，即保证其留有冗余电量以便配合实时调度。

在用户侧与发电侧二者构成的互动博弈模型中，用户侧是根据发电侧制定的分时电价s来进行用电量响应的，故而相应地用电响应量r则看作为发电侧分时电价函数，本文即是求取二者达到纳什均衡状态时的最优解，即最优用电负荷与最优分时电价。

首先在假设电价si已知的前提下求取用户侧效用函数最大化时的最优电量响应r＊i（si），然后将其带入发电侧效用函数w1中进行优化，并求得相应最优分时电价s＊i。

令用户侧效用函数w2对ri（si）求偏导并整理可得：

式中：κi＝－αiβi＞0；θi＝（αi－1）－1＜0。

进行二阶求导之后发现：

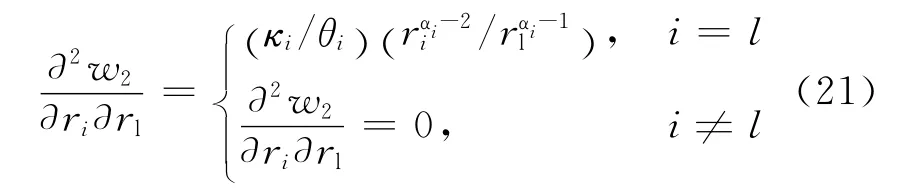
不难看出，此时因αi＜1，αiβi＜0故θi＜0，κi＞0，故可判定Hessian矩阵为负定，即可得到关于既定电价si的最优用电负荷r＊i（si）。

然后将此最优负荷带入发电侧效用函数进行寻优，即

从而得到函数w1最优时相应最优电价s＊i，如此循环往复进行迭代运算，又因si为ri的反函数，即si（ri）＝κi（－ri/ni）1/θi，此时相应约束条件式（15）、（16）、（17）可转化为

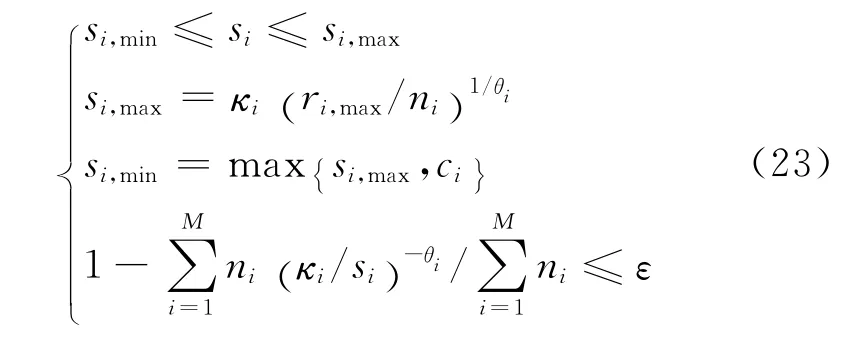
2.3 VPP内部优化流程

VPP的内部优化流程图见图3。

3 算例仿真

由于本文侧重研究虚拟电厂内部发电侧与用户侧之间互动博弈关系下的能源配置问题，并有意引导用户按照可再生能源出力走势进行用电，故而暂不考虑其与外部电力市场的交易问题。设定VPP内部各DG及储能装置相关参数，其中包含柴油发电机3台，额定出力分别为25，25，30kW，其发电成本参数aG＝－0.085，bG＝1.45，cG＝1.1，维护成本系数为0.086 2元/kW；风机5台，参数为vci＝3.5m/s，vco＝25m/s，vR＝10m/s，维护成本系数为0.031 4元/kW；光伏阵列3组，总额定出力45kW，维护成本系数为0.007 8元/kW；储能单元1组，额定容量110kW·h，维护成本系数为0.079 1元/kW；γ取0.02，ε取9%为宜，βi取1。本文优化流程利用Matlab优化工具箱进行实现。

根据风速、光照强度以及温度等日前预测基础数据绘制相应日前风电及光伏出力预测曲线，并同时给出未来24h内用户需求负荷曲线，如图4所示。

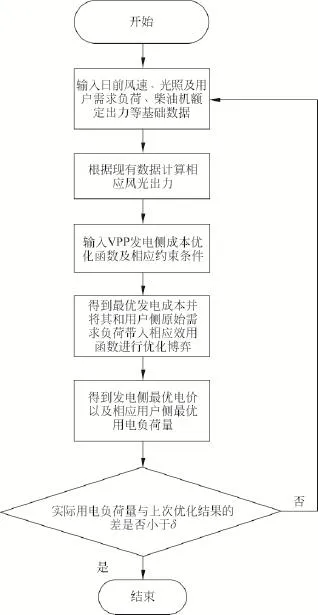
图3 VPP内部优化流程Fig.3 Flow chart of optimization in VPP

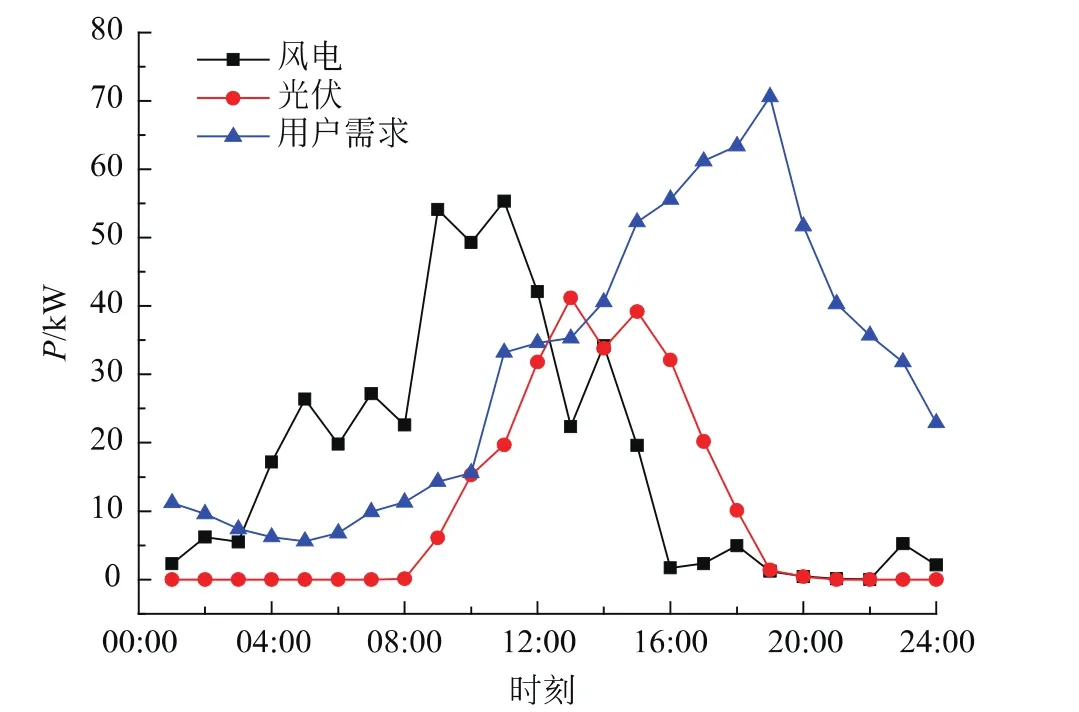
图4 风光出力及用户需求负荷日前预测曲线图Fig.4 Prediction diagram of the capacity of WT，PV and users'demand load

本文分别采用传统峰谷分时电价和博弈优化电价2种策略进行对比分析，给定峰平谷三阶段电价分别为2.82，1.78，0.91元/（kW·h），相应划分时段则分别13：00—22：00；08：00—13：00，22：00—01：00；01：00—08：00。经优化后结果如表1所示，相比于博弈电价优化策略，采用传统峰谷电价时，VPP内部发电侧收益略高，为986.72元，但同时会使用户在给定电价条件下为保证效用函数最大化而过于增大其可中断负荷比例，严重降低了用电舒适度，进而造成不便。经博弈优化后的用户实际负荷曲线及分时电价曲线分别如图5、6所示。不难看出，优化后的负荷曲线较原始需求负荷曲线来说更贴近可再生能源出力曲线，而且灵活的新型分时电价策略不会因某些时段价格过高过于固定而使用户因被迫断电失去舒适度。

表1 2种策略模式下用户用电量及发电侧效益Table 1 Users'electricity consumption and benefit of power generation side in two kinds of strategy mode

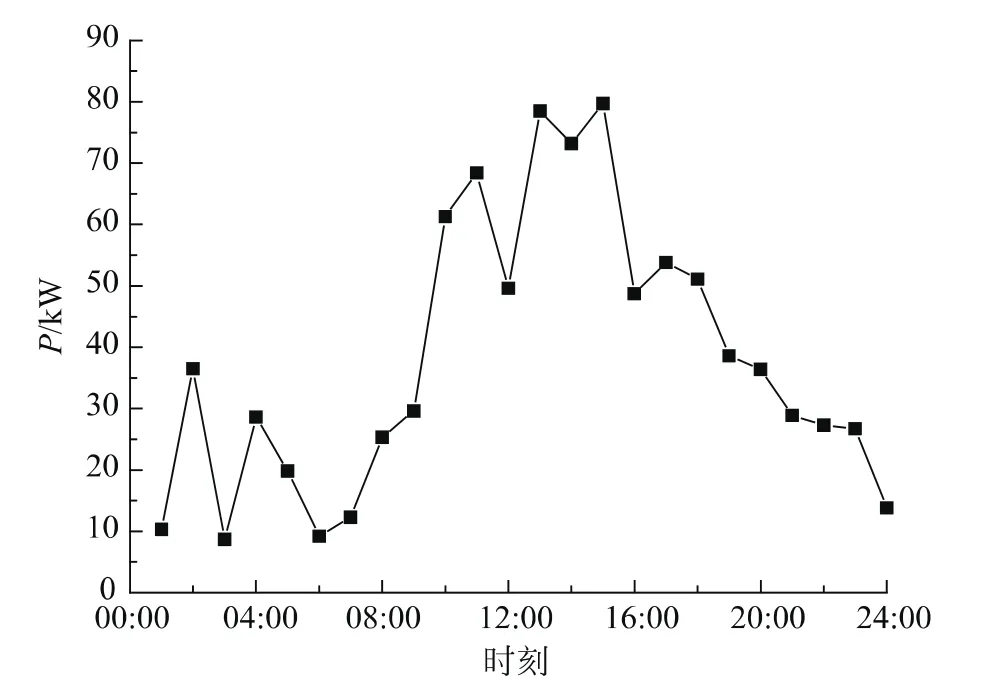
图5 博弈优化后用户实际负荷曲线Fig.5 Users'actual load curve after game optimization

4 结论

本文运用了非合作博弈模型对VPP内部发电侧与用户侧的互动关系进行了描述，同时考虑到用电满意度及各自保持绝对理性等条件，旨在实现能源利用率及运行经济最优。仿真结果表明，基于VPP内部发电侧与用户侧互动博弈的策略模型，得到相比于传统更合理的分时电价，充分考虑用电满意度指标，有力保障消费者权益，并使用电负荷曲线更契合可再生能源出力变化趋势，积极响应节能减排政策，同时也对发电侧经济效益起到优化作用，有效实现VPP内部能源的最优利用。

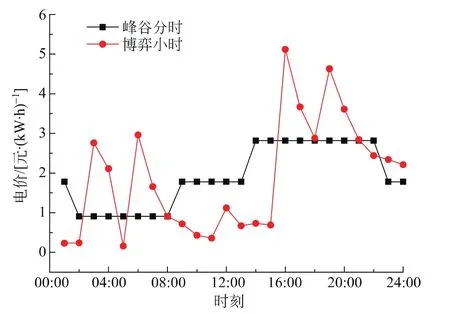
图6 2种电价策略曲线对比Fig.6 Comparison curve of the two kinds of electricity price strategy

［1］廖秀英，王婷，程辉，等.中国CO2能源排放量与CO2大气浓度时空分布研究［J］.湖南科技大学学报（自然科学版），2014，29（3）：103-107.LIAO Xiuying，WANG Ting，CHENG Hui，et al.Research on spatial and temporal distribution of carbon dioxide energy emission and concentration［J］.Journal of Hunan University of Science ＆Technology（Natural Science Edition），2014，29（3）：103-107.

［2］SIMS R E H，ROGNER H H，GREGORY K.Carbon emission and mitigation cost comparisons between fossil fuel，nuclear and renewable energy resources for electricity generation［J］.Energy Policy，2003，31（13）：1315-1326.

［3］KASMAN A，DUMAN Y S.CO2emissions，economic growth，energy consumption，trade and urbanization in new EU member and candidate countries：apanel data analysis［J］.Economic Modelling，2015，44（44）：97-103.

［4］BAYOD-RUJULA A A.Future development of the electricity systems with distributed generation［J］.Energy，2009，34（3）：377-383.

［5］KUMAGAI J.Virtual power plants，real power［J］.IEEE Spectrum，2012，49（3）：13-14.

［6］夏榆杭，刘俊勇.基于分布式发电的虚拟发电厂研究综述［J］.电力自动化设备，2016，36（4）：100-106，115.XIA Yuhang，LIU Junyong.Review of virtual power plant based on distributed generation［J］.Electric Power Automation Equipment，2016，36（4）：100-106，115.

［7］XIA Y H，LIU J Y.Optimal scheduling of virtual power plant with risk management［J］.Journal of Power Technologies，2016，96（1）：49-56.

［8］GIUNTOLI M，POLI D.Optimized thermal and electrical scheduling of a large scale virtual power plant in the presence of energy storages［J］.IEEE Transactions on Smart Grid，2013，4（2）：942-955.

［9］RUIZ N，COBELO I，OYARZABAL J.A direct load control model for virtual power plant management［J］.IEEE Transactions on Power Systems，2009，24（2）：959-966.

［10］余贻鑫，刘艳丽.智能电网的挑战性问题［J］.电力系统自动化，2015，39（2）：1-5.YU Yixin，LIU Yanli.Challenging issues of smart grid［J］.Automation of Electric Power Systems，2015，39（2）：1-5.

［11］孙宇军，李扬，王蓓蓓，等.计及不确定性需求响应的日前调度计划模型［J］.电网技术，2014，38（10）：2708-2714.SUN Yujun，LI Yang，WANG Beibei，et al.A day-ahead scheduling model considering demand response and its uncertainty［J］.Power Systems Technology，2014，38（10）：2708-2714.

［12］董朝阳，赵俊华，文福栓，等.从智能电网到能源互联网：基本概念与研究框架［J］.电力系统自动化，2014，38（15）：1-11.DONG Zhaoyang，ZHAO Junhua，WEN Fushuan，et al.From smart grid to energy internet：Basic concepts and research framework［J］.Automation of Electric Power Systems，2014，38（15）：1-11.

［13］陈春武，李娜，钟朋园，等.虚拟电厂发展的国际经验及启示［J］.电网技术，2013，37（8）：2258-2263.CHEN Chunwu，LI Na，ZHONG Pengyuan，et al.Review of virtual power plant technology abroad and enlightenment to China［J］.Power Systems Technology，2013，37（8）：2258-2263.

［14］卢强，陈来军，梅生伟.博弈论在电力系统中典型应用及若干展望［J］.中国电机工程学报，2014，34（29）：5009-5017.LU Qiang，CHEN Laijun，MEI Shengwei.Typical applications and prospects of game theory in power system［J］.Proceedings of the CSEE，2014，34（29）：5009-5017.

路 尧

（编辑 蒋毅恒）

Economic Optimization Operation of Virtual Power Plant Considering the Users'Satisfaction Based on Non-Cooperative Game Theory

LU Yao，LIU Jichun，XU Lixiong
（School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，Sichuan Province，China）

Nowadays the energy problems are gradually paid attention，the development of distributed generation（DG）and network communication technology relieves the strain on energy demand，improves the environment problems，and increases the permeability of renewable energy.But up to the present day，the optimization study of the common virtual power plant（VPP）focuses more on the energy scheduling of the internal DGs and the supply of the ancillary services such as market transactions for the external power grid etc.However，the common research fails to consider the load diversity and the electricity flexibility of the user demand，and the initiative and interactivity participating in internal energy scheduling as resources of demand side response.On this basis，the non-cooperative game theory is employed to build the interaction model of the power generation side and the demand side of users in this study.This model provides a theoretical basis to solve problems such as how to improve the interaction flexibility between the power generation side and the demand side of users，considering the satisfaction of users，gaming with their respective maximization of benefit as the goal.The simulation results verify the feasibility of the proposed theory，and compared with the traditional VPP optimization solution the method can realize the economic optimality of both the power generation side and the users'load side considering the users'satisfaction.Moreover，the proposed method improves the utilization rate of renewable energy and realizes the economic optimal operation of the VPP.

non-cooperative game；virtual power plant（VPP）；customer satisfaction；economic optimization

2017-01-11

路 尧（1989），男，硕士研究生，主要从事电力系统混沌振荡、电力市场及能源互联网方面的研究工作；

刘继春（1975），男，博士，教授，硕士生导师，主要从事电力系统分析及电力市场方面的研究工作；

许立雄（1982），男，博士，讲师，本文通信作者，主要研究方向为电力系统稳定与控制，xulixiong＠163.com。

TK01；TM62

A

2096-2185（2017）01-0023-07

10.16513/j.cnki.10-1427/tk.2017.01.004