交流系统故障时MMC-HVDC系统的控制策略

李 辉，张 琪，梁 栋，王林川

（1.东北电力大学电气工程学院，吉林吉林132012；2.国网山东电力公司平邑县供电公司，山东平邑273300；3.国网吉林省电力有限公司吉林供电公司，吉林吉林132300）

交流系统故障时MMC-HVDC系统的控制策略

李 辉1，张 琪2，梁 栋3，王林川1

（1.东北电力大学电气工程学院，吉林吉林132012；2.国网山东电力公司平邑县供电公司，山东平邑273300；3.国网吉林省电力有限公司吉林供电公司，吉林吉林132300）

交流系统故障时，基于模块化多电平换流器（modular multilevel converter，MMC）的柔性直流输电（voltage sourced converter-high voltage direct current，VSC-HVDC）系统的控制策略研究具有很重要的工程意义。为了解决传统的串级PI控制策略存在的PI调节器数量多、控制参数调试困难、系统的稳定工作区域小等缺点，设计了新的控制策略。文章分析了交流系统故障时MMC的特性，设计了基于反馈线性化原理的正负序双电流控制策略，该控制策略在交流电网正常及故障状态下均具有良好的控制性能。进一步分析了在负序电流得到抑制的情况下，直流侧电压和电流产生二倍频波动的原因，并且设计了直流电压纹波抑制器 （direct current voltage ripple suppressing controller，DCVRSC）。通过仿真软件PSCAD/EMTDC验证了文章设计的控制策略的正确性。结果显示，与传统的串级PI控制策略相比，本文设计的控制策略的参数调试简单，系统的稳定性高，直流电压的波动得到有效抑制。

模块化多电平换流器 （MMC）；柔性直流输电 （VSC-HVDC）；反馈线性化原理；双电流控制；直流电压纹波抑制器（DCVRSC）

0 引言

近年来，随着可再生能源的大规模开发利用，传统的输电方式已经不能满足新能源并网和远距离输电的要求。基于电压源换流器的高压直流输电（voltage sourced converter-high voltage direct current，VSC-HVDC）系统相比于传统的直流输电具有很大的技术优势［1－2］。这种输电技术能够快速实现有功功率和无功功率的独立解耦控制，能够向无源网络或弱交流系统供电，不需要站间通信，并且可以构成多端直流系统。此外，该技术还能够同时向交流系统进行有功功率和无功功率的支援，以提高输电系统的稳定性［3］。因此，大量的基于电压源型换流器的柔性直流输电工程被相继投入运行，然而这些工程主要是基于两电平或三电平的拓扑结构，存在串联器件动态均压、开关损耗大等问题。模块化多电平换流器（modular multilevel converter，MMC）以其可以进行模块化设计、开关损耗低、输出波形质量高、电平易于扩展等优势成为柔性直流输电领域非常具有应用前景的一种拓扑结构［4］。

自从模块化多电平换流器问世以来，国内外学者对模块化多电平换流器型高压直流输电（modular multilevel converter-high voltage direct current，MMC-HVDC）系统的稳态控制策略进行了大量研究，然而这些控制策略大多只适用于电网正常状态，针对交流系统故障时MMC-HVDC系统的特性分析和控制策略研究则显得较为不足［5－6］。MMC-HVDC系统是一个强耦合、多变量、非线性的系统，一般的控制策略很难满足控制要求，文献［7］中提出的基于串级PI调节的控制策略，虽然能达到理想的控制效果，但是却存在PI调节器数量多、控制参数调试困难、系统的稳定工作区域小等缺点。因此，有必要寻找一种更加理想的控制器。

本文将非线性系统反馈线性化理论应用到MMC-HVDC系统的数学建模和控制器设计中，所设计的控制器既能应用于电网正常状态，又能应用于电网故障状态。并且针对交流电网不对称故障时直流电压、电流存在二倍频波动的问题，设计一种直流电压波动抑制器，并在PSCAD/EMTDC上搭建仿真模型，验证所提出控制策略的正确性。

1 系统建模

1.1 工作原理

图1为模块化多电平换流器的电路图。如图1所示，换流器有3个相单元，每个相单元分为上下2个桥臂，每个桥臂由n个子模块和一个桥臂电抗器串联组成。图1中：L0为桥臂电感值；P和N分别为直流侧的正极和负极，O为直流侧中性点，在实际系统中并不存在。

MMC中每个子模块的结构图如图2所示，每个子模块包含1个储能电容，2个绝缘栅双极型晶体管（insulated gate bipolar transistor，IGBT）以及2个与之反并联的二极管。图中Usm为子模块的输出电压，ism为子模块的输出电流，Uc为子模块的电容电压。

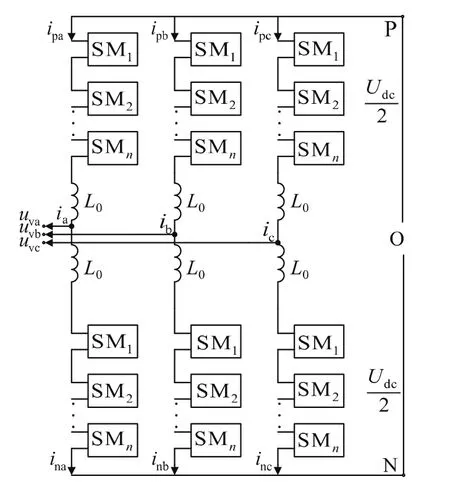
图1 MMC电路图Fig.1 Circuit diagram of MMC

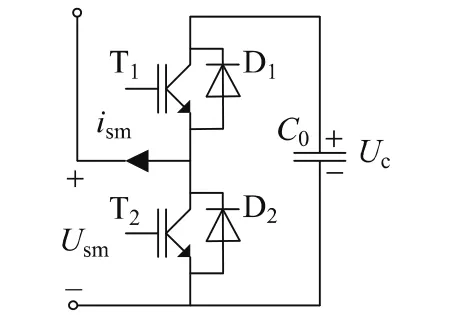
图2 子模块结构图Fig.2 Structure chart of submodule

直流侧的直流电压由3个相单元并联来维持，为了保证直流电压的稳定，任意时刻每个相单元中投入的子模块数必须是n个，通过改变相单元中n个投入的子模块在上下桥臂之间的分配来得到期望的交流输出相电压［5］。

1.2 换流站建模

图3为MMC单相等值电路图。如图3所示：V点为换流器的交流输出端，通过变压器与交流电网相连，这一点的线电流和相电压分别为ivj，uvj；L0为桥臂串联电抗，R0为桥臂等值电阻；Udc为直流侧电压，Idc为直流侧电流；桥臂电压可以用6个受控电压源upj、unj（j＝a，b，c）来等效，下角标p、n分别表示上、下桥臂；ipj、inj（j＝a，b，c）分别表示对应的各相上下桥臂相电流，参考方向如图3所示。

如图3所示，由基尔霍夫电流定律可得：

在j相单元中自上而下流动的电流为

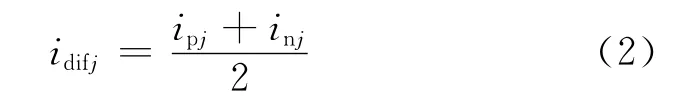
令Idc/3和iacj为idifj的直流分量和交流分量，则可得j相上下桥臂电流为：

图3 MMC单相等值电路Fig.3 Single-phase equivalent circuit of MMC

对j相上、下桥臂分别列写基尔霍夫电压方程可得：

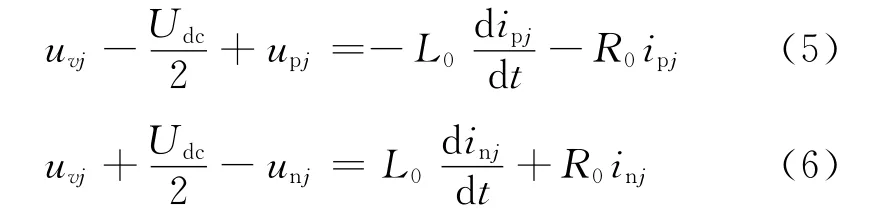
将式（5）和式（6）相加再除以2可得：

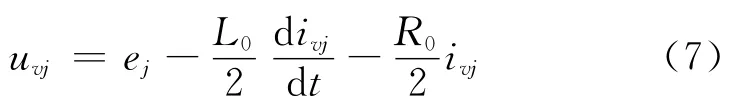
其中：

式（7）描述了换流器交流侧的动态特性。

将式（5）和式（6）相减再除以2可得：

式（9）描述了换流器直流侧的动态特性。

2 电网故障时的控制策略

2.1 电网不对称故障时换流站的数学模型

当电网侧交流系统发生不对称故障时，由于换流变压器一般都采用Y/△或△/Y的接线方式，可以隔离电网侧零序分量，因此只有正序分量和负序分量可以传递到换流器［8］。

将R＝R0/2，L＝L0/2代入式（7），并根据对称分量法，将式（7）分解为正序和负序2个独立的方程［9］：

式（10）中：上标“＋”和“－”分别表示正序分量和负序分量。

为了消除稳态误差、实现解耦控制，对式（10）施加同步dq坐标变换可得［10－11］：

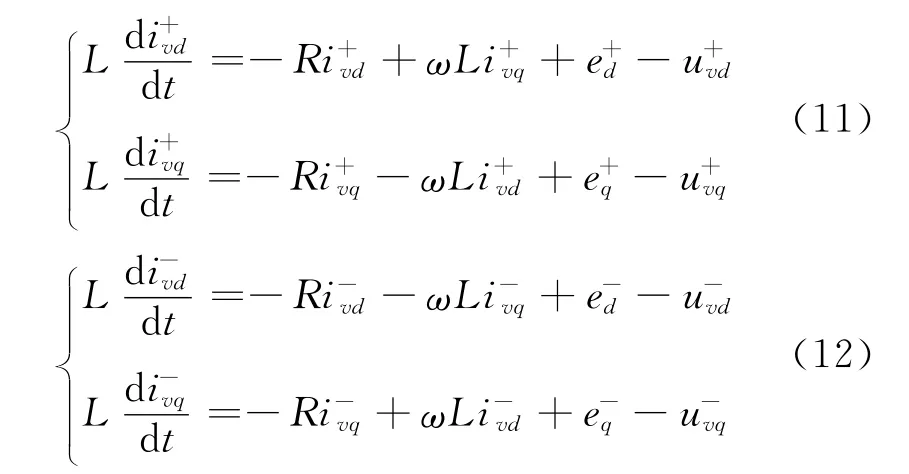
式中：ω为电网基波角频率。当换流站在正常状态下运行时，有。

2.2 控制器设计

2.2.1 内环电流控制器

为了提高控制系统的稳定性，在设计控制器时采用基于输入输出反馈线性化的电流解耦控制策略［12］。因此，将式（11）和式（12）变换成如下形式：

设正序分量子系统和负序分量子系统满足如下关系：

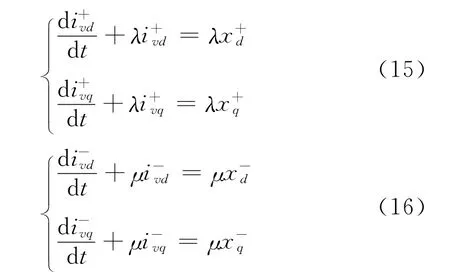
式（15）和式（16）中，λ和μ为比例控制参数。将式（15）和式（16）分别代入式（13）和式（14）并整理得：

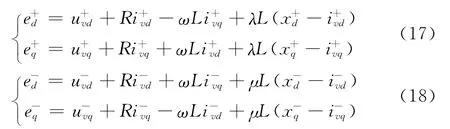
根据式（17）和式（18）可以设计出电网故障时的换流站的内环电流控制器结构如图4所示。

图4 内环电流控制器结构图Fig.4 Structure diagram of inner current controller

由图4可知，电网故障时的控制系统由正序电流控制器和负序电流控制器构成。图中的x＋d、x＋q分别代表正序有功电流和无功电流的参考值，x－d、x－q分别代表负序有功电流和无功电流的参考值。当电网正常运行时，不存在负序电压和负序电流，此时正序系统电流控制器输出的电压矢量即为换流器的调制波；当电网发生不对称故障时，电网中会存在负序电压和负序电流，为了抑制负序电流，将负序有功电流和无功电流的参考值设定为0。

2.2.2 外环控制器

正序有功电流和无功电流参考值来自外环功率控制器的输出参考值。为了简化控制器的设计，本文中外环功率控制器直接采用串级PI调制控制策略中外环功率控制器的设计方式，由此得到正序有功和无功电流的参考值［8］为

当换流器采用定直流电压控制时，正序有功电流的参考值为

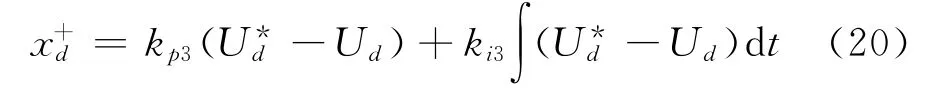
式（19）和（20）中的kp1、kp2、kp3和ki1、ki2、ki3分别为对应的PI控制器中的比例系数和积分系数。

3 直流电压波动抑制器

当交流电网发生不对称故障时，本文所设计的正负序电流控制能够很好地抑制交流电网中的负序电流，保持三相电流对称。但是由文献［10］的分析可知，当负序电流得到抑制时，直流侧电压和电流不可避免的会存在二倍频的波动，因此有必要提出一种以抑制直流侧电压波动为目的的控制策略，该控制策略能够和双电流控制策略相结合，在保证交流侧三相电流对称的同时，还能消除 MMCHVDC系统直流侧电压的二倍频波动。

A相上桥臂电压为

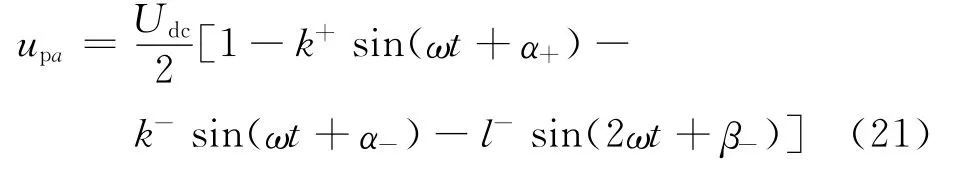
其中：

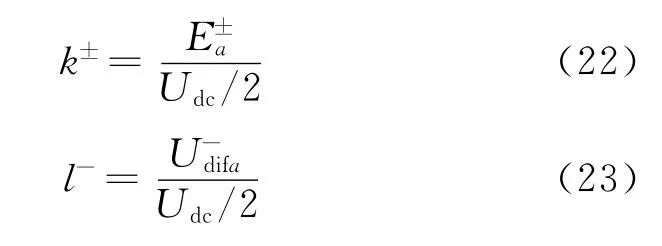
同理，A相下桥臂电压为

因为在交流电网发生不对称故障时，MMC产生的内部电动势的负序分量e－j将交流系统的负序电流抑制为零，所以并没有负序电流分量流入MMC的桥臂。与此同时，MMC的内部环流分量也被环流抑制器所产生的udifj抑制，因此，A相上下桥臂的电流就只包含直流分量和正序交流分量，式（3）和（4）可被重新表示为：

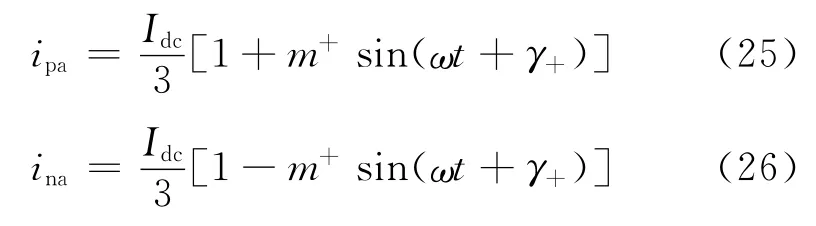
其中：m＋为正序电流调制比；γ＋为交流电网正序电流的初相角。

由式（21）、（24）、（25）、（26）可得A相的瞬时功率为

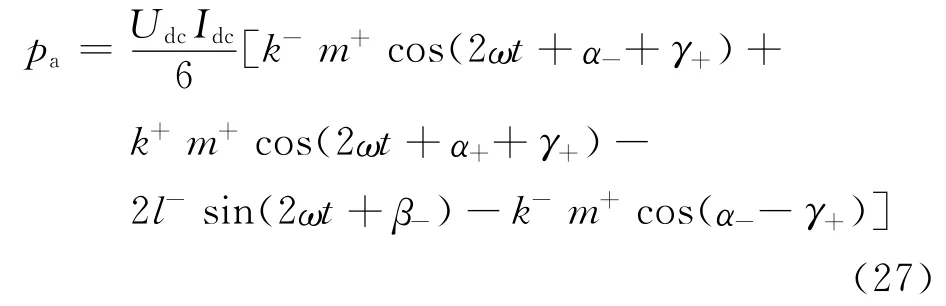
同理可得B、C相的瞬时功率为：

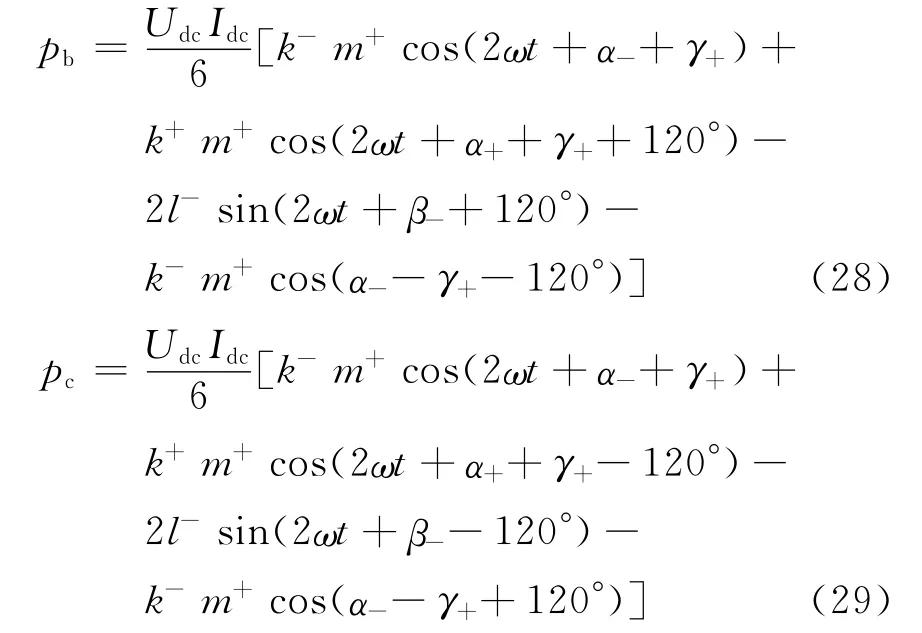
由式（27）、（28）、（29）可知，3个相单元的瞬时功率是由1个零序二倍频分量、2个负序二倍频分量和1个直流分量组成。由于零序分量无法相互抵消，因此只能通过直流线路传递到对端的换流站，造成直流电压和电流的二倍频波动，影响换流站的正常运行［13－14］。

通过以上分析可知，欲消除直流电压和电流中的二倍频分量，只有控制上下桥臂，使其输出的相单元电压中包含1个与前述的二倍频零序电压大小相等方向相反的分量，将之前的零序电压补偿掉，方可消除直流线路中的二倍频分量。直流电压波动抑制器的结构如图5所示。

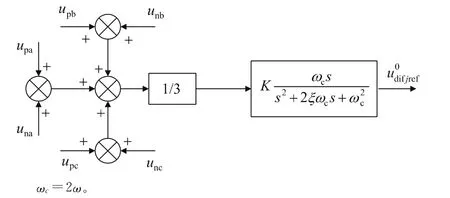
图5 直流电压波动抑制器Fig.5 DC voltage ripple suppression controller

直流电压波动抑制器产生的u0difjref与内环电流控制器产生的ej叠加后，再结合合适的调制策略即可得到相应的触发脉冲。

4 仿真算例

为了验证所提出的控制策略和直流电压波动抑制策略的正确性，基于PSCAD/EMTDC搭建了如图6所示的双端MMC-HVDC系统仿真模型。

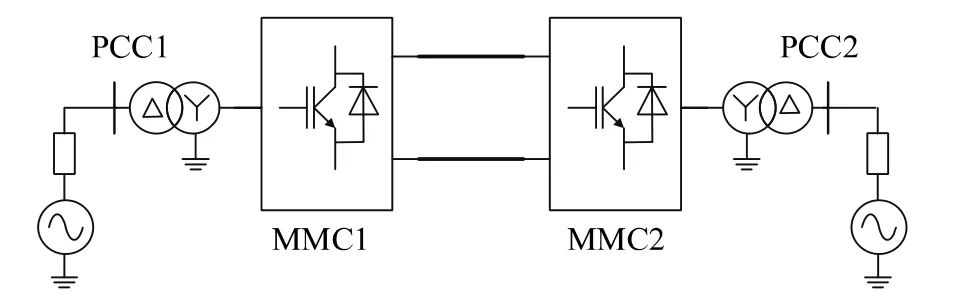
图6 MMC-HVDC系统结构图Fig.6 System structure diagram of MMC-HVDC

MMC1为整流站，采用定有功功率和定无功功率控制方式，MMC2为逆变站，采用定直流电压和定无功功率控制方式，仿真参数见表1。

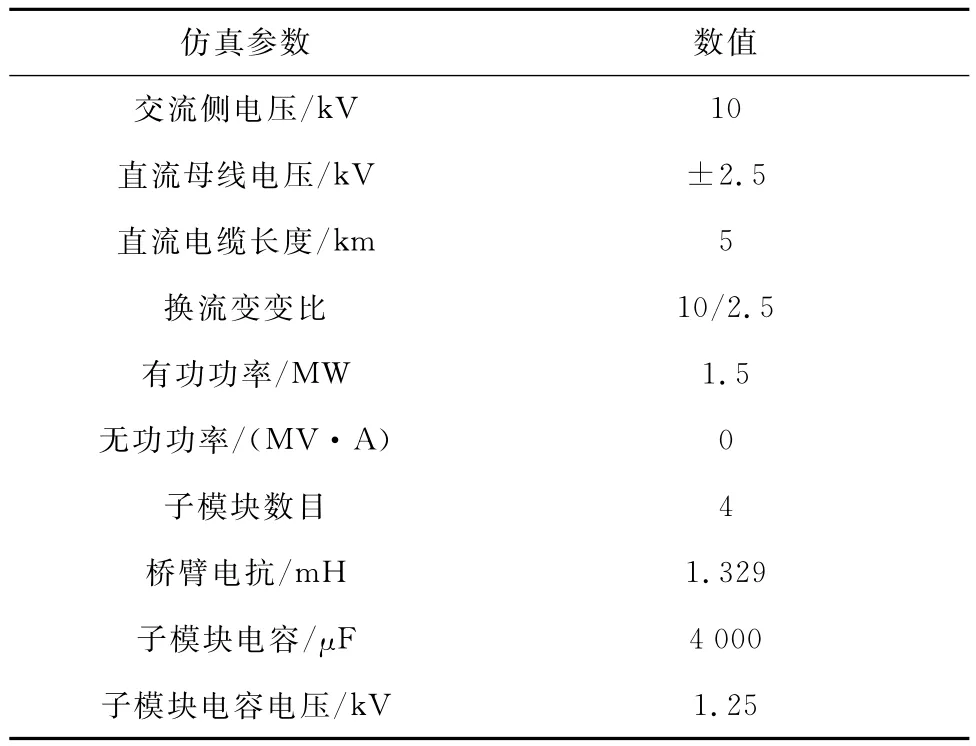
表1 仿真模型参数Table 1 Parameters of simulation model

当t＝3s时PCC1处发生C相接地故障，故障持续时间为300ms，t＝3.1s时直流电压波动抑制器投入运行。图7（a）是PCC1处的电网三相电压。图7（b）和图7（c）分别为整流站的交流输出电压和电流，如图7所示，文中所提出的双电流控制策略能够在故障情况下保证换流站输出的三相交流电流平衡。图7（d）为MMC1的C相上桥臂子模块电容电压。图7（e）和图7（f）分别为直流侧的电压和电流。如图所示，直流电压波动抑制器投入运行后，直流侧电压和电流的二倍频波动得到了有效抑制。图8（a）为PCC2处的电网三相电压，图8（b）和图8（c）为MMC2的交流侧输出电压和电流，图8（d）为MMC2的C相上桥臂子模块电压，由图8可知，当PCC1处发生单相接地故障时，所设计的正负序双电流控制器和直流电压波动抑制器能够保证对端换流站的正常运行。

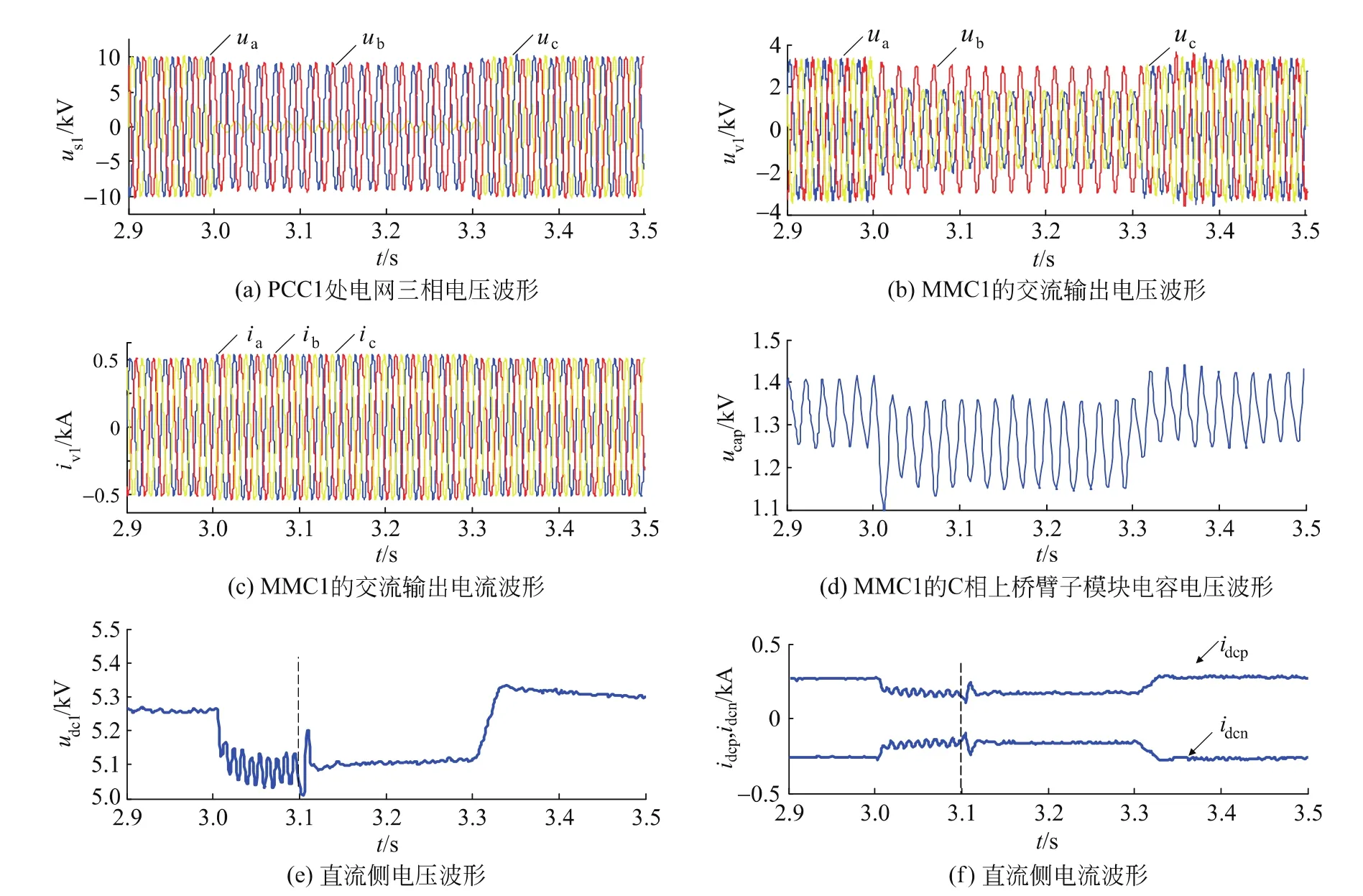
图7 MMC1仿真波形Fig.7 Simulation waveforms of MMC1

图8 MMC2仿真波形Fig.8 Simulation waveforms of MMC2

5 结论

本文通过分析模块化多电平换流器的工作原理，建立了故障状态下的数学模型，并且进一步设计了以保持三相电流平衡为目标的正负序双电流控制器。交流电网发生不对称故障，在负序电流得到有效控制的情况下，直流侧电压和电流仍存在二倍频波动的问题，基于此问题设计了直流电压波动抑制器。基于PSCAD/EMTDC的仿真验证了所设计的控制器的有效性。

［1］FLOURENTZOU N，AGELIDIS V G，DEMETRIADES G D，et al.VSC-based HVDC power transmission systems：An overview［J］.IEEE Transactions on Power Electronics，2009，24（3）：592-602.

［2］马成廉，潘文明，姚天亮，等.VSC-HVDC在交流电网非故障时的控制策略研究［J］.东北电力大学学报，2015，35（6）：26-32.MA Chenglian，PAN Wenming，YAO Tianliang，et al.Research on control strategy of VSC-HVDC in AC power grid［J］.Journal of Northeast Dianli University，2015，35（6）：26-32.

［3］徐政，陈海荣.电压源换流器型直流输电技术综述［J］.高电压技术，2007，33（1）：1-10.XU Zheng，CHEN Hairong.Review and applications of VSCHVDC［J］.High Voltage Engineering，2007，33（1）：1-10.

［4］蔡新红，赵成勇，庞辉，等.基于MMC欧拉－拉格朗日模型的HVDC不对称故障控制［J］.电力系统自动化，2013，37（17）：112-118.CAI Xinhong，ZHAO Chengyong，PANG Hui，et al.Control of HVDC transmission system based on euler-lagrange mathematical model of MMC under unbalanced faults［J］.Automation of Electric Power Systems，2013，37（17）：112-118.

［5］黄伟煌，李明，刘涛，等.柔性直流输电受端交流侧故障下的控制策略［J］.南方电网技术，2015，9（5）：27-31.HUANG Weihuang，LI Ming，LIU Tao，et al.Control strategy for VSC-HVDC under AC system fault of receiving end［J］.Southern Power System Technology，2015，9（5）：27-31.

［6］ANTONOPOULOS A，ANGQUIST L，NEE H P.On dynamics and voltage control of the modular multilevel converter［C］//Proceedings of European Power Electronics（EPE）Conference.Barcelona，Spain：IEEE，2009：1-10.

［7］GUAN M Y，XU Z.Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions［J］.IEEE Transactions on Power Electronics，2012，27（12）：4858-4867.

［8］管敏渊，徐政，潘武略，等.电网故障时模块化多电平换流器型高压直流输电系统的分析与控制［J］.高电压技术，2013，39（5）：1238-1245.GUAN Minyuan，XU Zheng，PAN Wulue，et al.Analysis and control of modular multilevel converter based HVDC transmission systems during grid faults［J］.High Voltage Engineering，2013，39（5）：1238-1245.

［9］DU C，SANNINO A，BOLLEN M H J，et al.Analysis of response of VSC-based HVDC to unbalanced faults with different control systems［C］//Proceedings of 2005IEEE/PES Transmission ＆Distribution Conference ＆Exposition：Asia ＆Pacific.Dalian，China：IEEE，2005：1-6.

［10］YAZDANI A，IRAVANI R.A unified dynamic model and control for the voltage-sourced converter under unbalanced grid conditions［J］.IEEE Transactions on Power Delivery，2006，21（3）：1620-1629.

［11］XU L，ANDERSEN B，CARTWRIGHT P，et al.VSC transmission operating under unbalanced AC conditions-Analysis and control design［J］.IEEE Transactions on Power Delivery，2005，20（1）：427-434.

［12］刘钟淇，宋强，刘文华.采用MMC变流器的VSC-HVDC系统故障态研究［J］.电力电子技术，2010，44（9）：69-71.LIU Zhongqi，SONG Qiang，LIU Wenhua.Research on the VSC-HVDC system using modular multilevel converters under fault condition［J］.Power Electronics，2010，44（9）：69-71.

［13］SAEEDIFARD M，IRAVANI R.Dynamic performance of a modular multilevel back-to-back HVDC system［J］.IEEE Transactions on Power Delivery，2010，25（4）：2903-2912.

［14］汤广福.基于电压源换流器的高压直流输电［M］.北京：中国电力出版社，2010.

（编辑 蒋毅恒）

Control Method of MMC-HVDC Systems During AC System Faults

LI Hui1，ZHANG Qi2，LIANG Dong3，WANG Linchuan1
（1.Institute of Electrical Engineering，Northeast Electric Power University，Jilin 132012，Jilin Province，China；2.Pingyi Power Supply Corporation of State Grid Shandong Electric Power Corporation，Pingyi 273300，Shandong Province，China；3.Jilin Power Supply Corporation of State Grid Jilin Province Electric Power Co.，Ltd.，Jilin 132300，Jilin Province，China）

With the framework of the modular multilevel converter（MMC），the research of control method for the voltage source converter-high voltage direct current（VSC-HVDC）systems plays an important role in the engineering application When AC system malfunctions.A new control method is designed to alleviate the challenging，i.e.，the large number of the PI regulator，the difficulty of the control parameter debugging，the narrow stable work area of the system.The character of MMC is analysized when AC system occurs faults，and with the assistance of the feedback linearization theory，a dual-current control method of positive-sequence and negative-sequence is introdued，which indicates that the proposed method has perfect control performance when AC system is normal and enconter a failure.The reasons that the DC voltage and current have second-order harmonics when negative-sequence current has been suppressed are further analysized，and a DC voltage ripple suppressing controller（DCVRSC）is designed.The accuracy of the proposed method is validated by the simulation software PSCAD/EMTDC.Compared with the common cascade PI control method，the proposed method has advantages such as the parameter debugging is simple，the stability of the system is high and the direct current voltage is suppressed.

modular multilevel converter（MMC）；voltage sourced converter-high voltage direct current（VSCHVDC）；feedback linearization theory；dual-current control；DC voltage ripple suppressing controller（DCVRSC）

2017-01-03

李 辉（1989—），男，硕士，主要研究方向为柔性直流输电技术，18744056956＠163.com；

张 琪（1991—），男，助理工程师，主要研究方向为智能配电网，838259199＠qq.com；

梁 栋（1983—），男，硕士，工程师，主要研究方向为继电保护技术；

王林川（1955—），男，硕士，教授，主要研究方向为电力系统运行分析，wlc550＠yeah.net。

TM721

A

2096-2185（2017）01-0016-07

10.16513/j.cnki.10-1427/tk.2017.01.003