数据缺失情况下函数型数据聚类方法及应用＊

高明慧，易丹辉，彭 锦，胡镜清，杨 燕

（1.中国人民大学应用统计科学研究中心 北京 100872；2.中国人民大学统计学院 北京100872；3.中国中医科学院中医临床基础医学研究所 北京 100700;4.中国中医科学院中医基础理论研究所北京 100700;5.湖北中医药大学 湖北 430065)

1 引言

随着现代科学的发展，越来越多的时间序列数据对于分析现实问题及预测有重要意义。为充分利用时间观测整体的信息，将时间观测作为连续函数关系进行深入分析，James Ramsay和Bernard Silverman在1982年提出函数型数据的分析方法[1]（Ramsay，1982）。函数型数据分析认为离散的时间序列观测由连续的时间上的函数产生，即离散观测背后存在着关于时间的连续函数。函数型数据的优势在于，一方面基函数拟合的思想提供了一种非参数的曲线拟合方法，不再拘泥于传统已知函数形式的参数方法；另一方面，将离散的观测连续化，通过求导运算可以更简便的分析个体在时间上的变化趋势[2]（Tokushige，2007）。

函数型数据分析的基本思想认为，时间序列观测背后真实存在连续时间上的函数影响观测的在不同时间的变化，因而寻找这一真实存在的函数关系是进行深入分析的关键。由于时间的连续性，函数曲线本质上是无穷维的，在一段时间内有无穷多个时间点，因此函数型数据在这一时间段内有无穷多个取值。但无穷维的数据无法使用传统的多元统计方法进行分析，因此将无穷维的连续曲线降维到有限维的空间非常重要。

原始的函数型聚类方法通过观测数据直接聚类[3]（Abraham，2003）。将每一个时间点看作一个变量，将离散时间点记录的数据看作多变量数据进行多元聚类分析。Shuichi Tokushige教授在2007年提出用改进的kmeans聚类方法进行函数型数据的聚类分析，即对每一个时间点上的样本观测进行kmeans聚类。样本在不同时间点所属的类别不同，反映了每一类样本不同的特点。这两种方法并不适用于含有缺失的函数型数据聚类分析。Catherine Sugar教授提出基于模型的自适应聚类方法，通过极大似然的方法估计参数，利用所有样本的观测值信息进行聚类，解决了缺失数据难以直接进行基函数拟合的问题。

事实上，自适应方法在含有缺失数据的函数型聚类问题中应用广泛。科罗拉多州立大学教授在2005年提出稀疏的函数型数据的自适应分析方法，其中提出利用函数型主成分分析法，在数据存在缺失情况下的函数曲线估计[4]。继而有学者在2008年提出针对稀疏数据的联合模型聚类方法，将函数曲线分解为固定效应和随机效应两部分，利用对数似然函数进行参数估计，从而实现函数型数据的聚类[5]。Peter Hall教授在2008年提出响应变量不服从连续的正态分布时的函数型数据分析方法，运用函数型主成分分析法对数据进行处理后，再根据主成分得分进行聚类分析[5]。其后，黄辉教授于2014年提出二分类变量函数型数据的联合模型聚类方法，并对于不同类别的方差进行了差异化设计，提高了聚类结果的准确性[6]。另外，李浩成教授在2014和2015年提出函数型数据的分层模型分析方法，将函数型数据分成样本个体、每天、每周的层次进行固定效应和随机效应的分析[7]。常微分方程[8]和生存分析[3]也可结合到函数型数据的分析当中。

本文第二部分介绍传统函数型数据聚类方法的局限性，第三部分介绍存在数据缺失情况下的自适应聚类方法，包括单变量时间观测和多变量时间观测两种情况。第四部分通过模拟比较处理缺失数据的函数型聚类方法，第五部分通过中医科学院提供的老年人宗气数据进行自适应聚类方法的实证分析。第六部分回顾了方法的介绍和实证结果，并对未来的研究提出展望。

2 传统函数型聚类方法的局限

传统函数型聚类方法包括直接利用原始数据聚类和筛选方法（filtering method）聚类。这两种方法在解决含有缺失的函数型数据聚类问题中均存在局限。

2.1 原始数据聚类的局限性

为解决时间序列观测的聚类问题，最朴素的聚类方法将每一时间观测点视为一个变量，离散时间点记录的数据看作多变量的函数型数据进行多元聚类分析。这种方法在大部分情境中并不适用。一方面，当时间点的取值过于密集或测量时间段较长时，时间的维度数高于样本数，聚类结果会受到维度过高的影响，尤其当变量数多于一个时，聚类分析的维度等于时间维度和变量维度的乘积，大大增加普通聚类分析的难度；另一方面，当样本之间的时间点取值不同时，这种聚类方法难以将观测时间点不同的样本统一看作多元数据，将离散的时间点转化为多维度的变量进行分析。另外，直接利用原始数据聚类忽视了时间上的连续性，不考虑时间先后的关系，会遗漏数据隐含的信息，导致分析结果不准确。在数据存在缺失的情况下，将每一个时间观测点当作一个变量进行多元聚类，会由于每个样本在多个变量上没有观测，无法进行聚类分析。

2.2 筛选法聚类（filtering method）的局限性

2.2.1 筛选方法的原理

Gareth James教授和Catherine Sugar教授首次将基函数拟合进行聚类的方法命名为筛选方法（filter⁃ing method）。筛选方法先用基函数对时间序列观测进行拟合和降维，然后再对有限维的函数型数据进行聚类。筛选方法的聚类依据是降维后系数之间的距离。筛选方法第一步利用基函数进行降维。基函数的形式记为

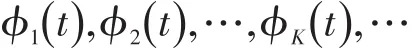
那么xi(t)即可表示为

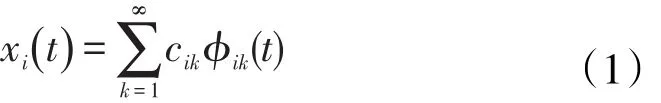
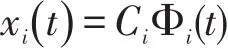
其中，基函数的选择可以是傅里叶基函数、样条基函数、小波基函数等。Ramsay的研究认为，当观测在时间上呈现明显的周期性时，可以选用傅里叶基函数；当观测没有周期性时，可以选用样条基函数；当观测存在频繁且剧烈的波动时，建议选用小波基函数[1]（Ram⁃say，2006）。

图1 某样本观测缺失时心律拟合值

当函数曲线表示为xi()t=CiΦi(t)时，为使得基函数能准确表示原函数，Ci的维度实际上是无穷维的，为了用更低的维度代替原始数据进行聚类分析，需要进行降维。

如果基函数表达的连续时间函数形式为，

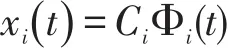
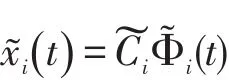
则可以有，使得

K即利用前K个基函数表示的时间函数x~i()t可以近似真实的时间函数xi(t)。这样通过牺牲一部分的准确性，完成了函数曲线从无穷维降到K维。由于样本的基函数选择相同，因此函数曲线可以由基函数系数代表，函数曲线之间的距离转化为基函数系数之间的距离，作为聚类的依据。

2.3.2 筛选方法的局限性

筛选方法的关键在于用有限个基函数系数表示函数曲线。在分析含有缺失的函数型数据时，每个样本由于数据缺失，观测数较少，只能通过较少的基函数拟合函数曲线，而过少的基函数会导致拟合效果不理想，与真实曲线相差较远的情况。如在宗气数据中，心率变量的取值一般在60至80之间。由于数据缺失较为严重，某样本在直接通过基函数拟合时，缺失部分的函数曲线的取值出现200以上或0以下的情况，如图1所示，与人的心率变化完全不符。从图1还可以看出，该样本在下午13点至18点的心率变量使用筛选方法得到的心率拟合值在17点之后迅速降低至-1 500以下，原因在于17点之后数据没有观测，拟合时缺乏足够的信息，导致基函数的拟合存在严重误差。当基函数系数无法代表函数曲线时，根据基函数系数进行聚类的结果是不准确的。

3 存在缺失的函数型数据自适应聚类

自适应方法是筛选方法的改进，筛选方法中基函数系数是固定的，在确定函数曲线拟合的基函数形式后，基函数的系数随之确定；而自适应方法中基函数系数是由类别中心决定的，并且存在随机效应。类中心由该类别中所有样本决定，因而，某个样本的系数不仅仅由这个样本自身的观测决定，还受属于同一类别的其他样本的影响，故其系数可根据样本所属类别不同而变化。一方面保证基函数系数的灵活性，另一方面借助类内不同样本的信息，使用最大似然法确定样本所属类别，在数据存在缺失的情况下可以有效补充缺失部分的信息。

自适应方法不仅适用完整时间观测的函数型数据聚类，还用于含有随机缺失的函数型数据聚类[9]（James，2003）。由于自适应方法同时确定样本的系数和样本所属类别，因此需要迭代算法进行计算，本文在求解过程中选用EM算法。

3.1 自适应聚类方法的优势

利用原始数据进行聚类，在处理含有缺失的函数型数据时，一方面会遇到时间观测不完整，多数时间点观测有缺失的问题，无法将n个时间点看作n个多元变量进行多元聚类；另一方面，当时间点过多时，多元聚类的变量维度过高，运算量非常大。筛选方法在对含有缺失的函数型数据进行聚类时，若每个样本的观测数较少，会使选用的基函数个数较少，难以对函数曲线进行较为准确的拟合，从而导致基函数系数之间的距离无法很好代表函数曲线之间的距离，致使聚类结果不准确。

自适应方法需事先确定基函数种类、个数和聚类个数。这种方法不直接使用基函数系数进行聚类，而是在已知分布信息的情况下，给定类中心系数等参数的初始值，运用EM算法，得到类中心对应系数的估计值；再根据函数型曲线的系数与类中心之间的马氏距离进行聚类。

3.2 单变量函数型数据的聚类

令gi(t)是第i个个体在时间t上的真实值，Yi(t)是第i个个体在时间t上的观测值，ϵi是第i个个体的测量误差。真实值等于观测值与测量误差的叠加。

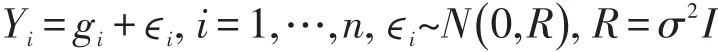
其中，s(t)是p维样条基函数向量，ηi是服从正态分布的基函数系数向量。由于基函数的系数的随机效应，ηi可以表示成与类别相关的固定效应μzi与随机效应γi之和。（3）式是真实函数曲线由无限维向p维空间的投影，即第一次投影。

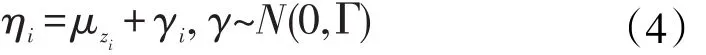
其中，zi表示个体i所属类别。James和Sugar认为样条基函数的系数αi根据所属类别k不同，服从均值为μk，方差为Σ的混合高斯分布。对于第k类的类中心μk，

其中λ0和αk分别为p维和h维向量，Λ是 p×h维矩阵，其中h≤min(p,G-1)。（5）式是p维的类中心 μk向h维空间中αk的投影，即第二次投影。在保证不损失信息的前提下进一步降维，一方面减少了待估参数，另一方面使高维情况下的聚类结果可视化。结合（3）、（4）、（5）、（6）式可以得出函数型聚类的模型。

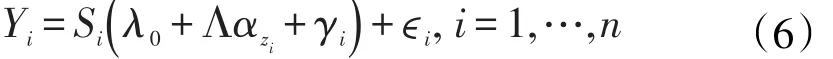
其中，n是个体数量。E()ϵi=0，测量误差之间、测量误差与gi之前均为独立。真实的函数可以用基函数进行拟合。

在自适应模型中，假设ϵi和γi都服从均值为0的正态分布。

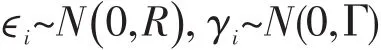
为保证模型可以求得唯一解，需要对λ0,Λ,αk加上两个约束条件。

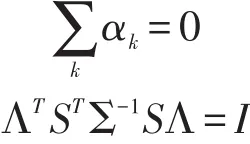
根据参数的分布假定可以得出，参数的极大似然函数可以写成

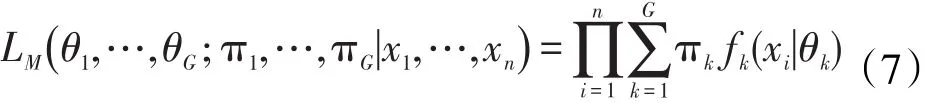
通过EM算法求解（7）式极大似然的最大值可以估计出样本所属类别πk，残差项方差Γ，随机扰动的方差σ2，截矩项λ0，投影矩阵Λ，投影后的类中心系数αi。α^i与αk之间的马氏距离决定了曲线i属于第k类的概率，即可以通过（8）式得出聚类结果。

其中，

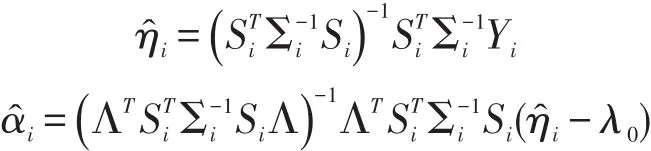
另外，通过参数的估计值可以得出曲线的拟合结果。借助第k类的信息，可以计算出完整时间区间内基函数的系数η^Mi，将基函数系数的估计值η^Mi

与基函数Si相乘，即得到曲线的拟合值。

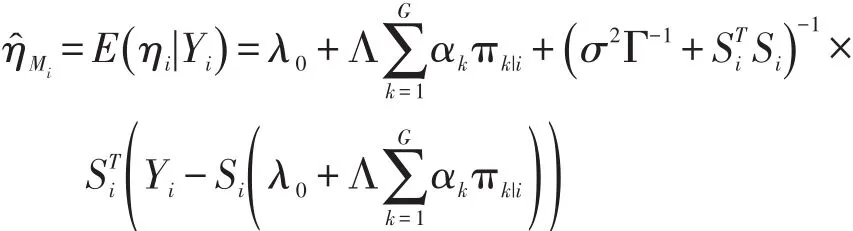
其中，

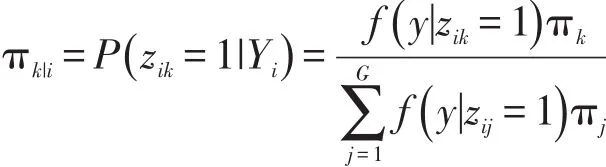
3.3 多变量函数型数据的聚类

自适应方法同样可以处理存在缺失的多变量函数型数据。Yij代表时间点tij1,…,tijnij上，第i个个体在第j个变量上的观测值，J为变量个数。Yij=(Yijtij1,Yijtij2,…,

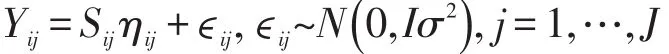
与上述过程相似，模型的形式为，

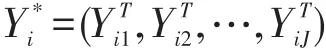
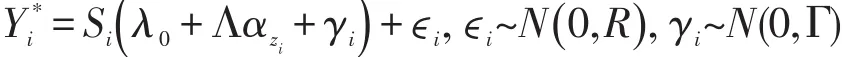
同样可以用EM算法估计参数，判断个体所属类别，画出拟合曲线的方法与单变量分析相似。

4 模拟设定

本文通过模拟比较不同缺失比例下函数型数据聚类方法的可行性，说明自适应方法在处理缺失数据时的优势。可行性是指在多次重复的实验中，该方法可以进行聚类分析的次数占总实验次数的比例。

在重复多次的情况下，由于每次随机生成的数据不同，缺失位置不同，聚类方法在相同缺失比例情况下，运行结果并不相同。模拟生成来自3个类别的100个样本，每个样本有60个时间观测。由（3）式，样本观测等于误差ϵ加上基函数s(t)与系数η的乘积。即其中对于所有样本，s(t)取基函数个数为10的B样条基函数。第一类有20个样本，η1为(η1,1,η1,2,…,η1,10)，10个元素取自均值为-10，方差为5的正态分布。第二类有30个样本，η2η1为(η2,1,η2,2,…,η2,10)(η1,1,η1,2,…,η1,10)，10个元素取自均值为0，方差为5的正态分布。第三类有50个 样 本 ，η3η2η1为 ( )η3,1,η3,2,…,η3,10(η2,1,η2,2,…,η2,10)(η1,1,η1,2,…,η1,10)，10个元素取自均值为10，方差为5的正态分布。误差ϵ服从标准正态分布。每个观测时间点上随机缺失的比例分别设定几种情况：1%，2%，5%，10%，20%。模拟设定实验重复1000次，记录成功进行聚类的次数，并计算该次数与总重复次数的比例。

Yi=gi+ ∈i,i=1,…,n,ϵi～N(0 ,R),R=σ2I，gi(t)=s(t)Tηi。

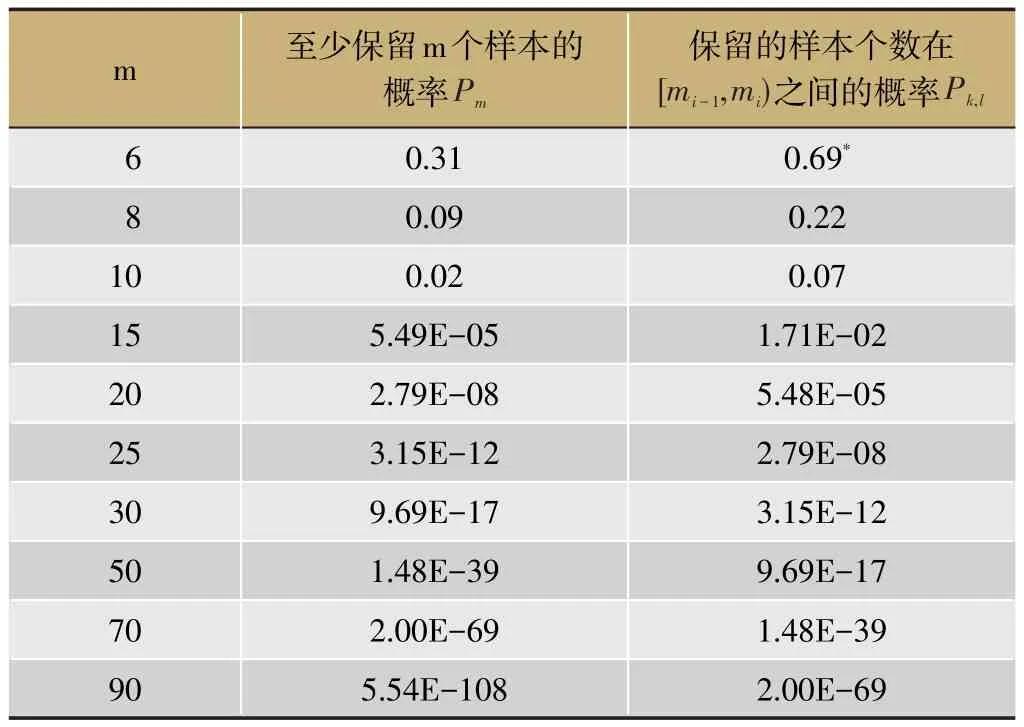
表1 5%缺失下保留m个样本的概率

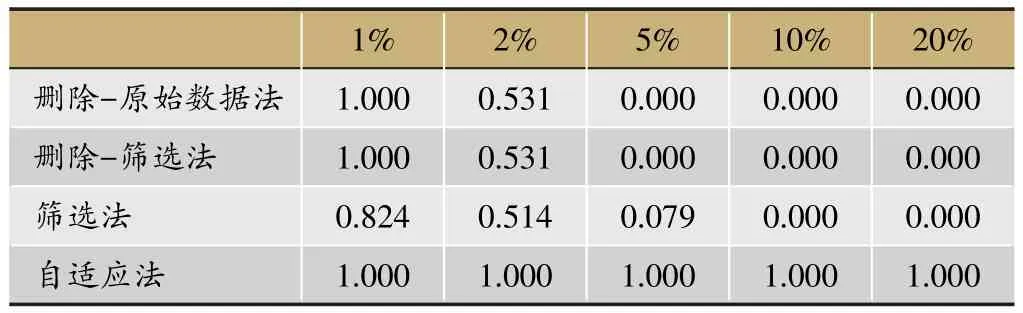
表2 不同缺失比例下聚类方法的可行性结果

对于删除法，即“直接丢弃含缺失数据的记录”[23]的方法，当剩余完整观测的样本数量大于等于30时，认为处理后的数据集足够代表原数据集的特征，可以进行聚类分析。对于筛选法，数据需要保证最小二乘估计的矩阵满秩，估计出基函数系数后进行函数型聚类。对于自适应法，只要EM算法可以进行最大似然估计，就可以进行函数型聚类分析。

结合处理缺失数据的删除法和不同聚类方法，模拟设定以下4种情况比较：删除法处理缺失数据，得到完整数据后通过原始数据法进行函数型聚类（下记“删除-原始数据法”）；删除法处理缺失数据，得到完整数据后通过筛选法进行函数型聚类（下记“删除-筛选法”）；直接使用筛选法进行函数型聚类（下记“筛选法”）；使用自适应法进行函数型聚类（下记“自适应法”）。其中原始数据法和筛选法由于自身的局限性，需要通过删除法得到完整的数据以进行聚类分析；而自适应法本身可以处理含有缺失数据的函数型聚类，不需要删除数据，因此不进行删除法与自适应法结合的聚类。

一般在缺失比例较低时可以使用删除法，但是当缺失比例较高，即模拟设定中缺失比例为5%及以上时，被删除的样本可能比较多，剩余样本无法代表原数据集进行后续分析。表1以缺失比例5%的情况为例说明保留m个样本的概率。令缺失比例为c，未被删除的样本个数为m，至少保留m个样本的概率为

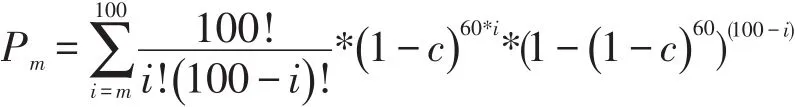
剩余样本个数在[k,l)之间的概率为Pk,l

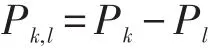
当m等于30时，至少保留30个样本的概率为9.69E-17，十分接近0，说明经过删除法处理后的样本个数在30个以上的概率非常低。当m等于6时，保留的样本个数小于6的概率为0.69，说明在缺失比例为5%的情况下，处理后的样本个数很可能剩余不到6个。在1 000次的模拟中，每次剩余样本的个数均不到30个，因此删除法不可行。

不同缺失比例下聚类方法的可行性结果如表2所示。

从表2可以看出，原始数据法、筛选法在缺失比例为1%时，数据经过删除法处理剩余较多样本，可以进行聚类分析；在缺失比例小于等于2%时，方法可运行的比例在50%以上；当缺失比例达到5%时，样本被删除的概率很大，“删除-原始数据法”和“删除-筛选法”不再可行。缺失比例大于5%，三种方法基本失效。

因此，前三种处理含有缺失数据的函数型数据聚类方法在缺失比例达到10%及以上时均不可行，只有自适应法可以进行缺失情况下的函数型聚类分析。在实例分析中，老年人的宗气数据在下午13点至18点之间的缺失比例高达70%，因此只能选择自适应法对该数据进行函数型聚类分析。

5 应用

5.1 数据形式

数据来源于中国中医科学院提供的老年人宗气数据。宗气的概念来自中医，主要指人体内脏的消化运输、升清降浊的功能。宗气主宰着机体心肺枢机的功能活动，是心肺功能交互为用的结果和产物（温武兵，2000）[10]。人体的心率、动脉血氧饱和度、体温、呼吸频率等特征可以反映宗气足或不足。通过分析这些数据可以对老年人宗气状态进行分类。

数据形式为仪器检测的58位老年人一天24小时内的心率、动脉血氧饱和度、体温和呼吸频率。经过数据清洗，截取下午一点至六点的时间序列观测，每五分钟取值一次，每个个体有60个观测值。由于仪器本身的准确性以及老年人使用操作的影响，部分数据存在缺失，删除缺失比例95%以上的个体，剩余52位老年人的观测纳入分析。根据心率、动脉血氧饱和度、体温、呼吸频率四个变量对人群聚类，在含有缺失数据的情况下使用多变量自适应方法进行函数型数据聚类。

5.2 聚类分析

5.2.1 基函数个数的选择

在Ramsay的2006年的函数型分析书中提到，函数曲线不存在周期性时一般选用B样条基函数进行拟合，而基函数个数的选择可以借鉴BIC和CV等方法，也可以主观选择，基函数个数只要在合理的区间内，对于分析结果的影响并不明显。周教授11在成对的稀疏函数型数据联合模型分析一文中也提到，基函数主要起到平滑函数曲线的作用。在宗气数据的研究中，本文将函数型数据进行了两次投影，最终将无穷维的函数型数据降维至二维平面中，因此基函数主要起到了将离散的时间数据转化为函数曲线这一作用，降维后基函数个数对于聚类结果的影响较小。另一方面，由于宗气数据的稀疏性，当所有样本需要用相同个数的基函数进行拟合时，最多只可以选用10个基函数。

本文通过十折交叉验证(ten-fold cross validation)的方法确定基函数的个数，结果如图2所示，其中横轴为基函数个数，纵轴为交叉验证的残差平方和。由于样本观测的稀疏性，52个个体中在下午一点至六点之间观测数最少为10个。Ramsay在函数型数据分析中提到，为保证基函数二阶导的连续性，基函数的个数最少取4个。另外，基函数个数不应大于个体的观测数，因此本文选择基函数个数的交叉验证的范围为4至10个基函数。评判基函数的拟合效果的标准为，残差平方和（Sum of the Squared Errors,SSE）越小拟合效果越好。从图2看，适宜选择10个基函数进行拟合。

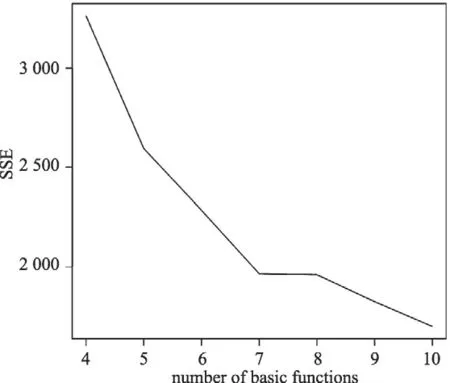
图2 基函数个数的交叉验证结果

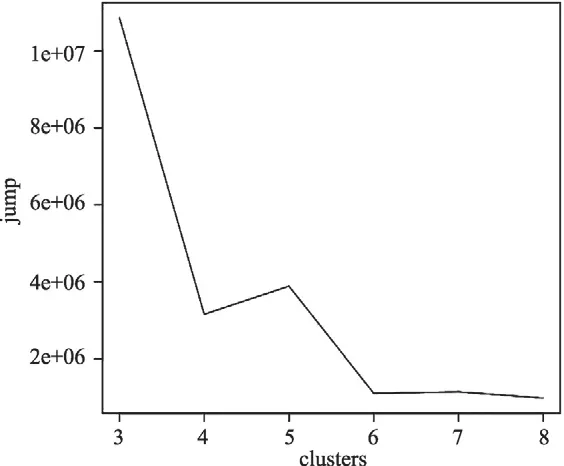
图3 聚类个数的选择碎石图

5.2.2 聚类个数的选择

聚类个数的选择一方面需要考虑分类的效果，使类内距离更小，类间距离更大。参考James和Sugar提出的原则，使用平均类内马氏距离dK确定聚类个数。

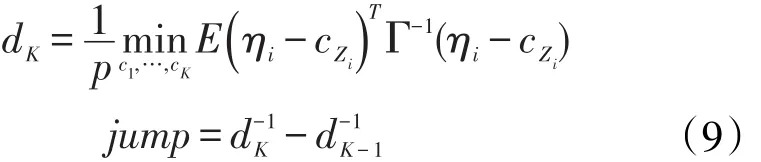
根据（9）式类内马氏距离的变化选择聚类个数。图3中纵轴为（8）式求得的类内距离之差jump，横轴为聚类个数。Jump越大，说明类内距离的变化越大，分隔不同个体的效果越明显。从图3中可以看出，聚成三类时jump最高，说明统计学上聚成三类是合理的。另外，结合宗气水平的中医理论，人群可分为宗气充足、宗气水平一般、宗气不足三种，因此聚成三类在实际应用中有现实意义。

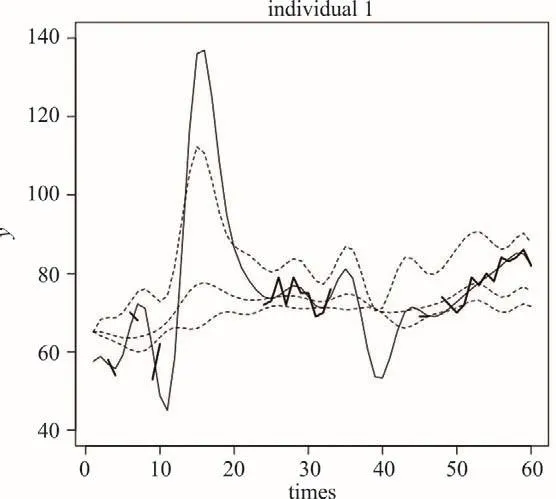
图4 某个体的观测值与拟合值

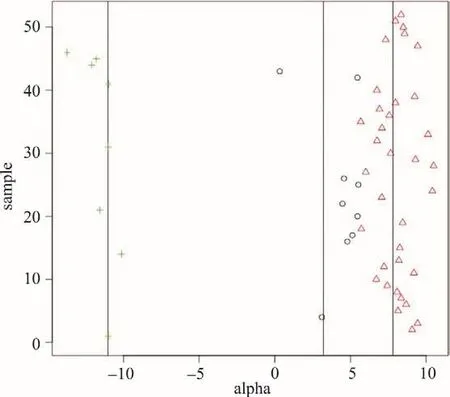
图5 聚成三类的样本在低维空间中的α值

5.2.3 聚类结果的解释

图4中粗实线代表一个体的含有缺失数据的观测值，细实线代表个体的拟合值，虚线代表三个类别的平均水平。从图4中可以看出，个体的观测值存在缺失因而观测曲线有多处间隔，而通过自适应方法的处理，个体的拟合值借助了三类平均水平的信息，因此可以得到连续的平滑的拟合值。这是自适应方法的优势之一。

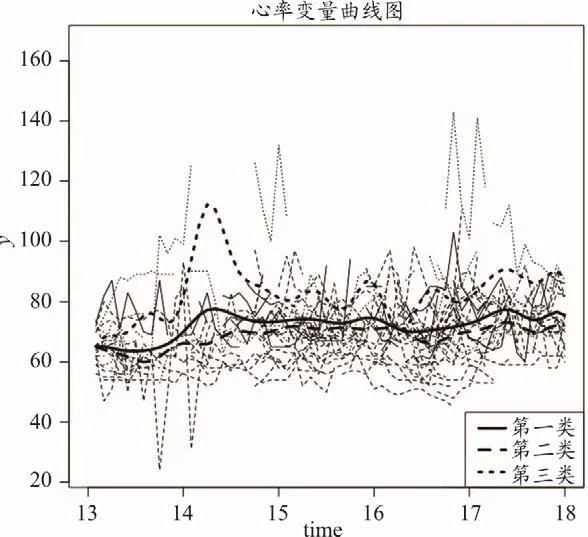
图6-1 三类个体在心率变量上的表现

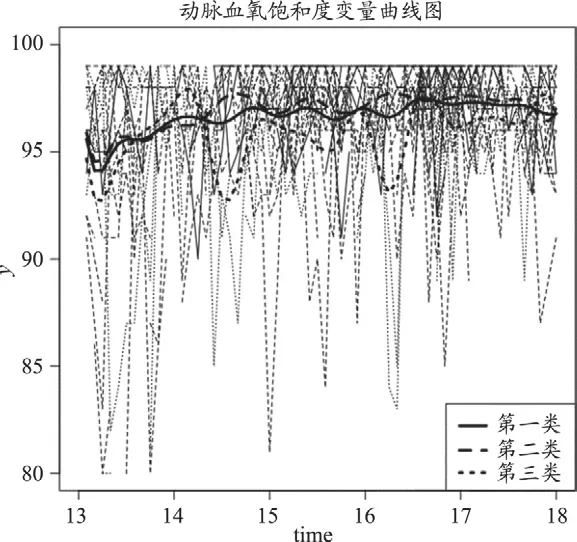
图6-2 三类个体在动脉血氧饱和度变量上的表现

考虑到聚类结果的解释意义，可以将老年人的宗气水平划分为三类。聚成三类的结果如下所示。图5横轴为个体降维后的α值，纵轴代表样本编号。中间两条竖线代表两类的均值。当类内样本的α值较为集中，类间样本的α值距离较远时，即说明样本的聚类效果较好。图5中圆圈代表第一类样本在低维空间的投影，三角形代表第二类样本在低维空间的投影，十字代表第三类样本在低维空间中的投影。可以看出第一类样本所对应的α值在3左右，第二类样本所对应的α值在8左右，第三类样本所对应的α值在-12左右，第三类和另外两类的α值分隔较为清晰，类中心相距较远，第一类和第二类之间也有一定的区别。因此可以认为统计上的聚类效果较好。

三类人群在心率、动脉血氧饱和度、体温、呼吸频率四个变量上的表现不同。在心率方面，第三类人群的心率较快，且波动较大，在13点至14点之间出现了明显的峰值；第一类人群和第二类人群的心率均较为平稳，其中第二类人群的心率相比于第一类人群更慢。

在动脉血氧饱和度方面，第一类人群的动脉血氧饱和度较为平稳，呈现缓慢上升的趋势。第二类人群的动脉血氧饱和度稍有波动，第三类人群的波动最为明显，其平均水平也低于前两类人群。

在体温方面，第一类和第二类人群的体温较为相近，在13点到14点之间，和15到16点之间有小幅度上升，整体波动不大。第三类人群的体温波动较为明显，尤其在16点之后，出现明显的下降和上升。总体上看，第三类人群的体温低于前两类人群。

在呼吸频率变量上，第二类人群的呼吸频率变化最为平缓，第一类人群的平均呼吸频率略高于第二类人群且略有波动。第三类人群的呼吸频率明显高于前两类人群，并且在14点、16点等时间点周围出现大幅波动。

综合四个变量的曲线图中信息可以看出，在下午13点至18点之间，第一类人群和第二类人群的特征较为相似，心率较慢且较为平稳；动脉血氧饱和度变化幅度小，且呈现缓慢上升的趋势；体温呈现小幅波动；呼吸频率变化平缓。其中第二类人群的心率和呼吸频率低于第一类人群。第三类人群在心率、动脉血氧饱和度、体温、呼吸频率四个变量上的波动幅度相对较明显，并且在心率和呼吸频率变量上水平明显高于第一类和第二类人群，在动脉血氧饱和度和体温变量上的水平略低于前两类人群。

中医理论发现，宗气不足的主要表现有心率快、血氧低、体温低、呼吸频率高，并且在每个变量上的波动幅度均比较大。因此可以认为，聚类所得三类人群中，第三类人群与第一类和第二类人群明显不同，有心率和呼吸频率较高、血氧含量和体温较低、四个指标均波动较大的特点，属于宗气不足人群。第二类人群相比于第一类人群的心率和呼吸频率更低，且波动幅度更加平缓，可以将第二类人群定义为宗气充足人群。第一类人群在各变量的水平介于第二类和第三类人群之间，与第二类宗气充足人群更为相近，因此可以将第一类人群定义为宗气水平一般的人群。

6 结论与讨论

本文主要介绍了函数型数据的特征，函数型数据的聚类方法以及中医科学院来年人宗气数据的实证分析。函数型数据分析的关键点在于降维，常用的降维方法是基函数法，用有限个基函数与系数的乘积表示连续的函数曲线。函数型聚类的方法有原始数据聚类法、筛选方法和自适应方法。原始数据聚类法当某些时间点上的样本观测存在较多缺失时，聚类方法无法计算样本所属类别，缺失比例增大，会导致无法进行聚类。筛选方法通过基函数法对函数曲线降维，再对基函数的系数进行多元聚类分析，当数据存在缺失时，拟合效果不理想，聚类效果不好，缺失比例增大也会出现无法聚类的情况。自适应方法在筛选方法的基础上，假定基函数系数根据样本所属类别不同服从不同的分布，这种方法提高了拟合的灵活性，并且适合处理稀疏数据的聚类问题。自适应方法也有其自身的局限性，一方面，当数据缺失过多，某些时间点上的观测值小于两个甚至没有观测时，自适应方法有可能无法运行。另一方面，本文仅讨论了自适应方法在缺失情况下进行聚类的可行性，其聚类效果有待进一步研究。本文讨论数据缺失的处理时，仅考虑了删除法，没有涉及插补法，因为当数据缺失较多时，插补的结果很可能是不准确的，基于插补数据的后续分析也很可能出现问题。函数型数据如何进行插补还有待研究。

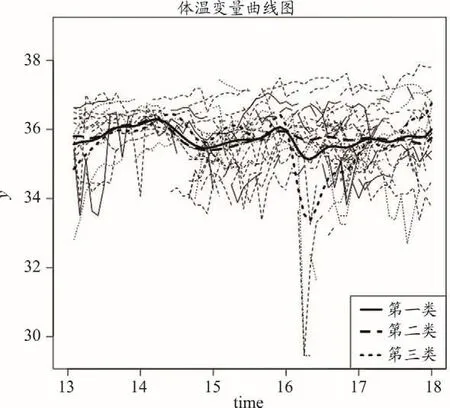
图6-3 三类个体在体温变量上的表现

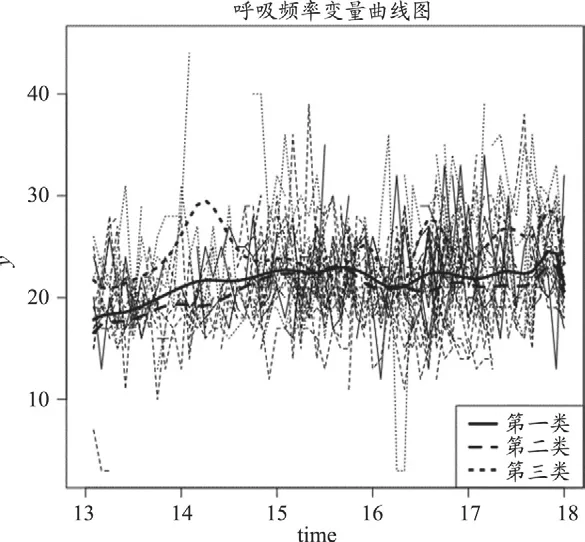
图6-4 三类个体在呼吸频率变量上的表现

应用部分主要分析了老年人在下午一点至六点的时间序列观测，通过心率、动脉血氧饱和度、体温、呼吸频率四个变量的聚类结果分析老年人宗气状况。利用针对含缺失数据的自适应聚类方法，将老年人分为宗气充足、宗气水平一般、宗气不足三类人群，其中宗气不足人群与前两类人群有明显差别。

本文中选取基函数个数的方法为交叉验证，使残差平方和最小的基函数个数为最优。由于拟合的函数曲线非线性，残差平方和难以反映拟合的效果，因此在未来的研究中可以考虑其他反应拟合效果的统计量代替残差平方和。另外，基函数个数的选择与样本观测数之间的关系也有待探究。自适应方法中，拟合每一条样本观测的基函数个数受样本观测稀疏性的限制，而聚类后每一类内的总观测数相对较充足，可以考虑扩大基函数个数的选择范围。

一般情况下，二次投影后的维度h选取1或2以保证可视化的效果。本文选择将无限维的函数曲线二次投影到一维空间上，在未来的研究中可以讨论将函数曲线投影到二维空间或更高维空间中的情况。

1 Ramsay J O.Functional data analysis.John Wiley&Sons,Inc.,2006.

2 Tokushige S,Yadohisa H,Inada K.Crisp and fuzzy k-means clustering algorithms for multivariate functional data.Comput Stat,2007,22(1):1-16.

3 Abraham C,Cornillon P A,Matzner-Løber E,et al.Unsuper⁃vised curve clustering using B-splines.Scandi J stat,2003,30(3):581-595.

4 Yao F,Müller H G,Wang J L.Functional data analysis for sparse longitudinal data.J Ame Stat Associ,2005,100(470):577-590.

5 Hall P,Müller H G,Yao F.Modelling sparse generalized longi⁃tudinal observations with latent Gaussian processes.J Royal Stat So⁃ci:Series B(Statistical Methodology),2008,70(4):703-723.

6 Huang H,Li Y,Guan Y.Joint modeling and clustering paired generalized longitudinaltrajectories with application to cocaine abuse treatment data.J Ame Stat Associ,2014,109(508):1412-1424.

7 Li H,Kozey Keadle S,Staudenmayer J,et al.Methods to as⁃sess an exercise intervention trial based on 3-level functional da⁃ta.Biostatistics,2015,16(4):754-771.

8 Little R J A,Schenker N.Missing data[M]//Handbook of statisti⁃cal modeling for the social and behavioral sciences.Springer US,1995:39-75.

9 James G M,Sugar C A.Clustering for sparsely sampled func⁃tional data.J Ame Stat Associ,2003,98(462):397-408.

10 温武兵.论宗气的生理功能.山东中医药大学学报,2000,24(4):247-250.

11 Zhou L,Huang J Z,Carroll R J.Joint modelling of paired sparse functionaldata using principalcomponents.Biometrika,2008,95(3):601-619.