深水网箱护栏力学性能分析及优化

刘海阳，王绍敏，黄小华，陶启友，胡 昱，郭根喜，宋利明



深水网箱护栏力学性能分析及优化

刘海阳1,2，王绍敏1,2，黄小华1,2，陶启友1,2，胡 昱1,2，郭根喜1,2※，宋利明3

（1. 中国水产科学研究院南海水产研究所，农业部南海渔业资源开发利用重点实验室，广东省网箱工程技术研究中心，广州 510300；2.中国水产科学研究院南海水产研究所热带水产研究开发中心，三亚572018； 3. 上海海洋大学海洋科学学院，上海201306）

护栏是深水网箱浮架系统不可或缺的重要构件，对支撑网衣、保持养殖容积、协同网箱浮架抵抗波浪流冲击起到重要作用。该文分别对中国当前应用的圆型深水网箱和六三型深水网箱护栏开展了弹塑性阶段的力学试验和有限元分析。结果表明：1）波流和气流的共同频率达到深水网箱护栏固有频率14.25 Hz时更易产生共振疲劳破坏；2）冲角为0°的集中载荷使护栏变形最大，此时扶手管中心为最易变形区域，立柱下端为最易破坏区域；3）同规格同材料的圆形扶手管抗形变能力显著大于六边形扶手管；4）扶手管的载荷-位移方程服从对数函数分布。护栏结构优化结果显示将管材的圆形截面处理为椭圆，护栏的水平抗弯性能增加6.58%。

有限元法；力学性能；高密度聚乙烯；深水网箱；护栏

0 引 言

圆型深水网箱是中国当前应用较广泛的主流深水网箱，其锚泊系统均为多点系泊；六三型深水网箱（网箱外浮管形成类三角形结构、内浮管形成六角形结构，故称“六三型”）为中国针对未来深远海养殖而开发的单点系泊深水网箱[1-4]。护栏是深水网箱浮架系统不可或缺的重要构件，对支撑网衣、保持养殖容积、协同网箱浮架抵抗波浪流冲击和为养殖工人提供安全工作环境起到重要作用，其结构安全问题是影响网箱系统可靠性的主要因素之一。在风浪流作用下，浮架随波浪做升沉运动[5-7]，护栏与浮管协同受力，浮架护栏可能会由于无法承受网衣和环境的过大载荷而导致破坏[8-10]。Fredriksson等[11]基于有限元模型对高密度聚乙烯（high density polyethylene，HDPE）浮管结构临界荷载条件的局部破坏准则进行了评估；王笛清等[12-13]对波流共同作用下的圆型网箱浮管结构应力和变形进行了有限元模拟；鄢奉林等[14]对圆型网箱浮管结构承载极限进行了有限元分析；Wu等[15-21]从不同角度研究了波流作用下圆型网箱的浮管受力及其运动变形。目前，国内外关于深水网箱的相关力学研究主要集中在网衣[22-23]、锚绳[24]及浮管[25]等方面[26-27]，而深水网箱护栏受力与极端荷载条件下的破坏机理及判定准则等尚未见报道。

本研究针对多点系泊圆型深水网箱和单点系泊六三型深水网箱的护栏部件分别进行了线性及非线性过程的力学试验和有限元分析，对比分析了圆型和六三型网箱护栏的力学特性、抗载荷能力以及可能的破坏条件和形式，以期为优化设计护栏、浮架系统和提升深水网箱系统极限承载力提供理论依据。

1 有限元分析模型

1.1 护栏有限元模型

护栏主要包括扶手管、三通、立柱和工字架（图1a）。护栏管材的结构及尺寸为国家标准（GB/T 13663.2－2005[28]），材料为高密度聚乙烯。根据护栏的结构及尺寸，利用Unigraphics NX软件构建护栏三维实体模型（图1b）。将Unigraphics NX护栏模型导入ANSYS Workbench软件进行有限元分析。由于护栏为圆柱体结构，故选用六面体网格进行自动优化网格划分，尺寸为20 mm× 20 mm，网格质量满足精度要求[12]。分别在ANSYS Structure模块内直接构建圆形和六边形扶手管模型。

a. 护栏结构尺寸

a. Structure size of guardrail

1.2 护栏模型数值求解

1）护栏弹性阶段的应力-应变方程依据胡克定律

式中为应力，MPa；为弹性模量，MPa；为应变。

2）护栏及扶手管静力学弹性分析的载荷-位移一元线性回归方程

式中为恒力，kN；为护栏刚度，kN/mm；为位移，mm。

3）扶手管塑性阶段的载荷-位移非线性方程

式中为载荷，kN；为位移，mm；1、2均为方程的系数。

4）扶手管塑性阶段的切线模量非线性方程

式中为切线模量，MPa ，为的导数。

5）扶手管应力-应变的非线性方程

式中为应力，MPa；1、2均为方程的系数。

6）扶手管塑性模量的非线性方程

式中′为塑性模量，MPa，为的导数。

7）有限元模拟与力学试验在弹性阶段的误差计算方法

式中Δε为误差率；E为有限元模拟值，MPa；其中=2代表护栏，=3代表扶手管；1为材料力学试验值，MPa。

8）管材截面弯曲正应力（在=max即横截面上离中心轴最远的各点处弯曲正应力最大）

式中σ为最大弯曲正应力，MPa；为弯矩，kN·mm；为抗弯截面系数，mm3。

9）管材截面拉压正应力

式中σ为截面拉压杆正应力，MPa；F为轴向载荷，kN；为横截面面积，mm2。

10）根据载荷叠加原理可知，管材截面最大正应力

式中σ为管材截面最大正应力，MPa。

1.3 护栏模型求解思路

护栏模型有限元计算的原理及思路：1）基于加权余量法，建立护栏初边值问题等价的积分表达式；2）护栏单元离散，将护栏区域划分为若干相互连接且不重叠的单元；3）护栏单元分析，确定护栏单元基函数；4）建立护栏总体有限元方程；5）设定护栏本质边界条件；6）求解护栏各节点的函数值。

2 材料与方法

2.1 护栏管材力学试验方法

2.1.1 力学性能测试方法

护栏管材的拉伸、压缩和弯曲强度分别参照GB/T 1040.1-2006[29]、GB/T 1041-2008[30]和GB/T 9341-2008[31]中的测试方法进行，使用的仪器为微机控制电子万能试验机（SCT-57（232））。

2.1.2 疲劳试验方法

护栏海上作业时会随波流和气流等产生运动响应[32]，若波流和气流的共同频率达到护栏的共振频率则易发生疲劳破坏。利用液压伺服疲劳试验机对护栏管材进行多批次疲劳试验[33]，设定工作频率为5 Hz，应力幅值为最大拉伸强度时所对应力值的80%（19.6 MPa），试件为光滑圆柱标准件，原理如图2所示[34]。

2.2 护栏有限元分析方法

2.2.1 模态分析方法

护栏模态分析的约束方式为：浮管两端为全约束，扶手管和立柱可自由振动。护栏模态分析的约束方式及模态分布场如图3所示。

2.2.2 静力学分析方法

1）六三型护栏

对护栏进行有限元静力学分析，根据护栏海上作业时的约束条件和载荷方式，抽象其力学模型。六三型护栏的约束方式为：1）浮管施加、、方向位移为0的紧固约束。工字架施加方向位移为0的约束，防止工字架在浮管上滑动，模拟注塑限位块对工字架的固定作用。护栏模型的载荷方式为：对1/12扶手管分别施加冲角为0°、45°、90°[35]的均布和集中恒力1～6 kN，该文选择冲角为90°、集中载荷为2 kN的分析结果进行示意，如图4a所示；条件下的位移、应力、应变的分布场分别如图4b、4c及4d。

2）扶手管

对比研究六三型深水网箱和圆型深水网箱扶手管的局部稳定性。HDPE扶手管建立各向同性材料双线性等向强化模型（bilinear isotropic hardening model for isotropic materials，BISO），切线模量设定为120 MPa[36]。护栏在海上使用过程中主要受到风流环境的均布载荷和网衣的集中载荷[37]。锚绳为单点系泊和多点系泊作业状态时，浮架随波浪移动，当浮架处于稳定状态时护栏迎风流载荷区域始终固定。故施加的约束及载荷为：将六边形和圆形扶手管围绕圆心平均分为12段，在每段节点处分别施加0°（方向）、45°（方向）、90°（方向）方向位移为0的约束，两节点之间的每段扶手管施加均布载荷。

3 结果与分析

3.1 护栏管材力学试验结果

3.1.1 力学性能测试结果

由护栏管材静力学试验，获得护栏的材料力学特性及破坏条件，见表1。其中拉伸强度、压缩强度、弯曲强度作为判定护栏管材失效的临界标准[38]。

表1 高密度聚乙烯（HDPE）护栏管材力学性能

3.1.2 护栏疲劳分析结果

HDPE护栏模态分析结果见表2。由表2可知，六三型护栏1～6阶振动模态固有频率为14.25～33.59 Hz，位移为8.07～12.77 mm，应力为6.370～21.658 MPa，应变为0.005 568～0.017 466；扶手管为振动位移最大区域，立柱为振动应力最大区域，护栏固有频率较低且共振位移、应力、应变均较小。通过疲劳试验可得拉伸疲劳断裂时间为23.5 h，疲劳断裂时间较短。根据振动理论可知，扶手管海上作业过程中可能达到1～6阶振动模态，扶手管与波流共振机率较高，更易导致护栏振动失稳和疲劳断裂。考虑到护栏的振动疲劳问题，应增加减震保护设施以满足振动强度要求。

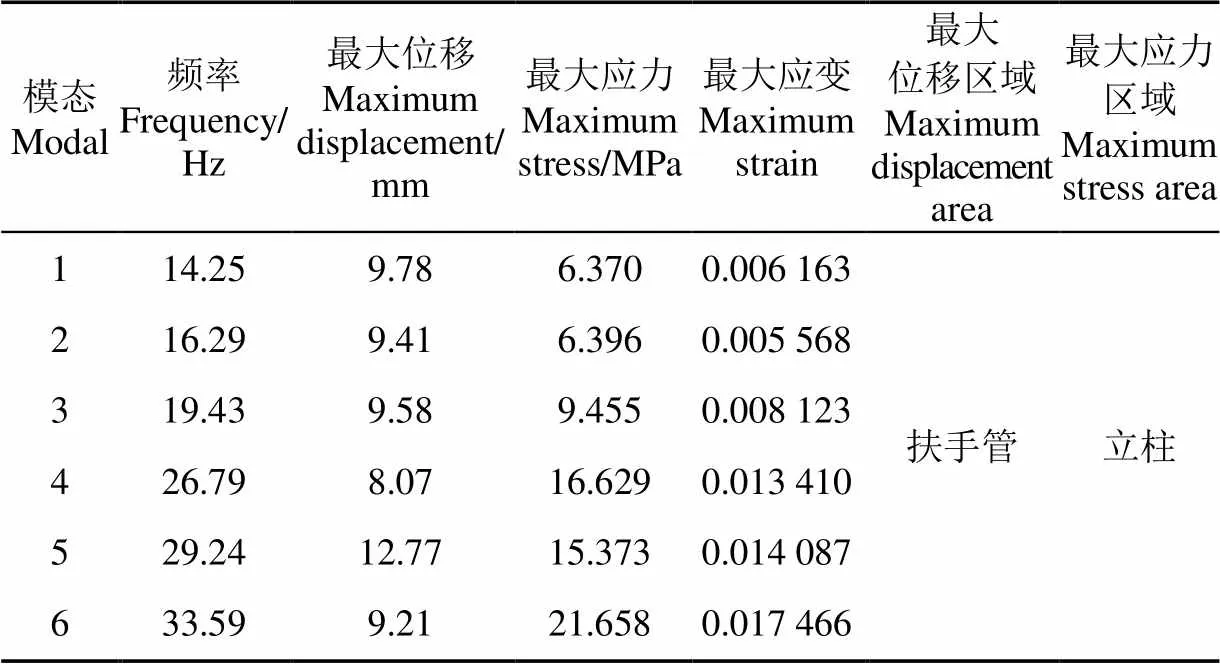
表2 HDPE六三型护栏有限元模态分析

3.2 护栏、扶手管有限元分析结果

3.2.1 六三型护栏弹性模拟结果

六三型护栏静力学分析结果（载荷为2 kN）的最大值及所在区域见表3，六三型护栏弹性变形阶段的载荷-位移、应力-应变方程皆采用一元线性回归的方法进行拟合，回归曲线如图5所示。

表3 HDPE六三型护栏有限元静力学分析（2 kN载荷）

由图5可得，六三型护栏刚度拟合方程见式（11）～（16），应力-应变方程见式（17）。

1）护栏均布载荷-位移弹性阶段拟合方程

T1=0.118 2L1,2=0.999 （11）

T2=0.168 5L2,2=0.999 （12）

T3=0.184 1L3,2=0.999 （13）

式中T为均布载荷，kN；L为均布载荷的位移，mm；1、2、3分别表示冲角为0°、45°和90°。

2）护栏集中载荷-位移弹性阶段拟合方程

T1=0.056 8L1,2=0.999 （14）

T2=0.075 3L2,2=0.999 （15）

T3=0.157 4L3,2=0.999 （16）

式中T为集中载荷，kN；L为位移，mm。

3）护栏弹性阶段应力-应变拟合方程

σ=1 132.5ε,2=0.987 （17）

式中σ为护栏线性阶段的应力，MPa；ε为护栏线性阶段的应变。

由表3可知，六三型护栏冲角为0°、45°、90°时，扶手管中心及两端的位移最大，为最易变形区域；立柱下端及三通的应力、应变最大，为最易破坏区域。由图5可知，不同冲角的位移、应力及应变表现为0°>45°>90°，集中载荷的位移、应力及应变均高于均布载荷，说明0°冲角的集中载荷对护栏的破坏强度最大。根据表3、式（14）、（17），冲角为0°、集中载荷为4 kN时，位移、应力、应变分别为70.47 mm、28.922 MPa、0.026 434，外力引起的最大应力大于HDPE材料的弯曲强度（25.2 MPa）时产生屈服断裂，导致护栏失效。为了提高护栏整体强度，可将管材形状由圆柱型优化为阶梯型（也可增加套管），以减小危险区域的曲率半径与管壳厚度比。

冲角为0°时，扶手管的最大位移区域为扶手管两端，而90°时的最大位移区域为扶手管中心，根据杠杆原理，扶手管两端连接区域无立柱的支撑保护作用，远端悬臂长度增大，从而使冲角为90°时的扶手管两端区域变形增大，表明立柱对扶手管的保护作用较明显，增加立柱数量能有效减小扶手管变形。

冲角为0°时，护栏最大应力、应变均在立柱底部区域，立柱受力形式可抽象为悬臂梁模型（受力点为三通区域，固定点为工字架区域）。可对立柱进行加固处理，在立柱底部增加肋板和筋骨件，或将圆柱型立柱优化为圆台型。冲角为90°时，护栏最大应力、应变均在扶手管与三通接触区域，受力形式为拉压杆模型（作用于立柱的受力作用线与立柱的轴线重合），扶手管与三通接触区域产生轴向压缩，增大立柱轴径或增大三通与扶手管接触面积，均可提高护栏强度。

3.2.2 扶手管弹性模拟

扶手管有限元静力学分析结果的最大值及所在区域见表4，扶手管弹性变形阶段的拟合曲线如图6。

表4 HDPE圆形、六边形扶手管有限元静力学分析（2 kN载荷）

由图6可得，扶手管刚度见式（18）～（23），弹性模量见式（24）。

1）圆形扶手管载荷-位移弹性阶段拟合方程

T1=0.446 4L1,2=0.999 （18）

T2=0.436 1L2,2=0.999 （19）

T3=0.429 2L3,2=0.999 （20）

式中T为圆形扶手管的载荷，kN；L为圆形扶手管的位移，mm。

2）六边形扶手管载荷-位移弹性阶段拟合方程

T1=0.172 2L1,2=0.999 （21）

T2=0.185 2L2,2=0.999 （22）

T3=0.191 1L3,2=0.999 （23）

式中T为六边形扶手管的载荷，kN；L为六边形扶手管的位移，mm。

3）扶手管弹性阶段应力-应变拟合方程

σ=1 236.7ε,2=0.998 （24）

式中σ为扶手管线性阶段的应力，MPa；ε为扶手管线性阶段的应变。

根据表1、式（17）和（24），HDPE弹性模量的试验值1=1 240 MPa，HDPE弹性模量的护栏模拟值2=1 132.5 MPa，HDPE护栏弹性模量的模拟误差为∆1=(2−1)/1×100%=8.669 4%<10%；HDPE弹性模量的扶手管模拟值3=1 236.7 MPa，HDPE扶手管弹性模量的模拟误差为∆2=(3−1)/1×100%=0.266 1%<10%。HDPE护栏及扶手管弹性模量的模拟误差均在数值模拟误差范围内（8.67%<10%，0.27%<10%）[39]。

由图6可知，同等载荷条件下的圆形扶手管位移、应力、应变皆小于六边形扶手管。双因素方差分析表明，在同等载荷条件下，六边形扶手管的位移显著大于圆形扶手管（=0.001 72<0.05），说明圆形扶手管的刚度大于六边形扶手管，圆形扶手管抵抗变形的能力较强。根据表4，圆形扶手管的载荷分布较均匀；六边形扶手管最大位移在六边形边角两侧区域，最大应力、应变均在六边形边角区域（出现应力集中）。因此，可在六边形扶手管边角处安装弯头（圆弧曲率过渡）以优化六边形扶手管。

由图6可知，六边形扶手管不同冲角下的位移表现为0°>45°>90°，应力、应变均表现为0°<45°<90°；圆形扶手管不同冲角下的位移表现为0°<45°<90°，应力、应变均表现为0°>45°>90°。对冲角为0°、45°、90°的有限元模拟结果进行双因素方差分析，=0.994 47>0.05，说明冲角对扶手管刚度无显著性影响。扶手管受力时可简化为简支梁模型（仅在两端受铰支座约束），扶手管主要产生弯曲应力。冲角为0°、均布载荷为6 kN时，位移、应力、应变分别为33.87 mm、27.202 MPa、0.022 012，应力大于扶手管的弯曲强度（25.2 MPa），此时六边形扶手管失效；冲角为0°、载荷为16 kN时位移、应力、应变分别为36.597 mm、25.932 MPa、0.020 914，此时圆形扶手管失效。

3.3 扶手管塑性分析

六边形、圆形扶手管塑性变形的拟合曲线如图7所示。

由图7可知，扶手管载荷-位移非线性方程见式（25）～（30），应力-应变非线性方程见式（31）～（32）。

1）六边形扶手管试验的载荷-位移方程

式中F、S分别为六边形扶手管试验的载荷（kN）和位移（mm），′为六边形扶手管试验的切线模量（MPa）。

2）六边形扶手管模拟的载荷-位移方程

式中F、S分别为六边形扶手管模拟的载荷（kN）和位移（mm），′为六边形扶手管模拟的切线模量（MPa）。

3）圆形扶手管模拟的载荷-位移方程

式中F、S分别为圆形扶手管模拟的载荷（kN）和位移（mm），′为圆形扶手管模拟的切线模量（MPa）。

4）扶手管模拟的应力-应变方程

式中σ、ε分别为扶手管非线性阶段的应力和应变，′为HDPE扶手管的塑性模量。

六边形扶手管载荷-位移的试验值与有限元模拟值进行对比研究，塑性阶段试验数据与有限元模拟数据的拟合曲线如图7a所示。进行双因素Kolmogorov-Smirnov (K-S)拟合优度检验，=0.122，=0.861 3>0.05，即扶手管非线性阶段的实测值与有限元模拟值无显著性差异。

该研究根据第四强度理论及等向强化Von Mises屈服准则判定扶手管塑性失效形式，失效形式主要是经过大量塑性变形而产生较大的残余伸长。应力-应变关系曲线反映了HDPE材料在受力条件下的内在变化规律。由图7b可得，扶手管随着应力增大，应变逐渐增大，且其变化速率逐渐加快，由弹性变形逐渐转变为塑性变形。由式（31）、（25）、（27）、（29）可知，扶手管应力-应变曲线（图7b）、载荷-位移曲线（图7a）均服从对数函数分布，且形状相似。以六边形扶手管为例，其载荷-位移曲线可简化为2个阶段：1）弹性变形阶段OE（点O为载荷为0时的初始点，点E为弹性变形过渡到塑性变形的临界点）；2）屈服极限强化（塑性硬化）阶段EB（点B为塑性变形过渡到缩颈变形的极限点），不考虑理想曲线中比例极限屈服（应变软化）过程及强度极限颈缩（断裂破坏）过程。根据图7a，圆形扶手管的弹性变形过程明显大于六边形扶手管，另外，载荷相同时六边形扶手管的塑性变形明显大于圆形扶手管，表明圆形扶手管的结构性能优于六边形扶手管。

切线模量（应变硬化模量）为材料屈服后塑性变形极限范围内的宏观模量，塑性模量为屈服极限和强度极限之间的曲线斜率（应力-应变函数的变化率）。该研究扶手管的切线模量方程、塑性模量方程皆服从反比例函数分布，施加载荷前期，扶手管变形的变化速率较小，随着载荷的增加，扶手管变形的变化速率会迅速增加。同等载荷条件下，圆形扶手管的切线模量（式（30））大于六边形扶手管（式（28）），表明圆形扶手管的变形速率小于六边形扶手管，进一步说明圆形扶手管的力学性能明显优于六边形扶手管。

4 护栏截面优化设计

根据壳体理论可知，护栏为薄壳杆静定结构，受力时为拉弯组合变形，其中扶手管主要产生弯曲应力，立柱主要产生拉压应力，可通过优化管材截面形状以提高护栏强度。

由式（8）可知，最大弯曲正应力与弯矩成正比，与抗弯截面系数（模量）成反比。抗弯截面系数为管材抵抗变形能力的指标且只与截面形状及中轴位置相关，其综合地反映了截面形状与尺寸对弯曲正应力的影响。由式（9）可知最大拉压正应力与轴向载荷成正比，与横截面面积成反比。由式（10）可知管材最大正应力为最大弯曲正应力与最大拉压正应力之和。

目前常用的护栏管材横截面为空心圆形，如图8a；扶手管管材压扁10%处理为空心椭圆，如图8b；优化立柱横截面近似为空心方形，如图8c。空心圆形、空心椭圆、空心方形的截面面积与抗弯截面系数表达式分别见公式（41）～（43）和（44）～（47），式中字母的定义见图8。均布载荷为2 kN时，空心圆形、空心椭圆、空心方形的截面面积与抗弯截面系数见表5。

1）护栏管材截面面积计算方程

空心圆形截面：

空心椭圆截面：

空心方形截面：

式中A为空心圆形截面面积，mm2；为空心圆形外径，mm；为空心圆形内径，mm；A为空心椭圆截面面积，mm2；为空心椭圆长轴外半径，mm；为空心椭圆长轴内半径，mm；为空心椭圆短轴外半径，mm；为空心椭圆短轴内半径，mm；A为空心方形截面面积，mm2；为空心方形外边长，mm；为空心方形内边长，mm。

2）护栏管材抗弯截面系数计算方程

空心圆形截面：

空心椭圆截面：

长轴方向：

短轴方向：

空心方形截面：

表5 护栏管材优化前后的截面面积及抗弯截面系数

注：1、2、3分别为空心椭圆（空心方形）管材与空心圆形管材的用料、拉压正应力、弯曲正应力的百分比增长率；、分别为空心椭圆的长轴短轴。

Note:1,2,3is the growth rate for hollow-oval (hollow-square) comparing with hollow-circle in terms of material, tensile normal stress and normal stress in bending respectively;,is the hollow-oval’s major axis and minor axis respectively.

由式（41）～（47）、表5可知，W<W<W<W，A<A<A。空心椭圆、空心方形抗弯截面系数与截面面积均大于空心圆形，管材截面优化后的最大弯曲正应力与最大拉压正应力皆小于优化前。故适当将管材作压扁处理有利于提高扶手管抵抗水平载荷的能力；立柱横截面采用近似方形有利于提高立柱刚度。空心椭圆、空心方形比空心圆形的用料分别增加0.50%、1.86%，空心椭圆、空心方形比空心圆形的抗压性能分别增加0.50%、1.86%；空心椭圆长轴的抗弯性能比空心圆形增加6.58%、短轴比空心圆形减少5.68%，空心方形的抗弯性能比空心圆形增加6.83%。

5 结 论

该文对深水网箱护栏系统的力学性能进行了弹塑性过程的试验分析和数值模拟，研究结果表明：

1）深水网箱护栏在振动频率为5 Hz时的疲劳断裂时间为23.5 h，当达到固有频率14.25～33.59 Hz时护栏产生共振，更易产生疲劳破坏。

2）冲角为0°的集中载荷对护栏的破坏性最大，此时立柱受力形式为悬臂梁模型；冲角为90°时护栏扶手管受力形式为拉压杆模型。扶手管中心及两端的位移最大，为最易变形区域；立柱下端及三通的应力、应变最大，为最易破坏区域。

3）同等规格的圆形扶手管刚度显著大于六边形扶手管，具备良好的抗形变能力。

4）扶手管非线性阶段的载荷-位移方程服从对数函数分布，切线模量方程服从反比例函数分布，反映了扶手管发生弹塑性变形的过程。

在未来设计网箱护栏系统时，可考虑将护栏管材适当压扁处理为空心椭圆，以利于提高护栏抵抗水平载荷的能力。

[1] 郭根喜，黄小华，胡昱，等. 深水网箱理论研究与实践[M]. 北京：海洋出版社，2013.

[2] 袁军亭，周应祺. 深水网箱的分类及性能[J]. 上海水产大学学报，2006(3)：350－358.

Yuan Junting, Zhou Yingqi. Classification of offshore fish cages and their performances[J]. Journal of Shanghai Fisheries University, 2006(3): 350－358. (in Chinese with English abstract)

[3] Xu T J, Dong G H, Li Y C, et al. Numerical study of a self-submersible single-point mooring gravity cage in combined wave-current flow[J]. Applied Ocean Research, 2014, 48: 66－79.

[4] Zhao Y P, Bi C W, Chen C P. Experimental study on flow velocity and mooring loads for multiple net cages in steady current[J]. Aquacultural Engineering. 2015, 67: 24－31.

[5] Huang X H, Guo G X, Tao Q Y, et al. Numerical simulation of deformations and forces of a floating fish cage collar in waves. Aquacultural Engineering, 2016, 74: 111－119.

[6] Li L, Fu S X, Xu Y W, et al. Dynamic responses of floating fish cage in waves and current[J]. Ocean Engineering, 2013, 72(7): 297－303.

[7] Bi C W, Zhao Y P, Dong G H, et al. A numerical analysis on the hydrodynamic characteristics of net cages using coupled fluid-structure interaction model[J]. Aquacultural Engineering, 2014, 59(2): 1－12.

[8] 吴常文，朱爱意，沈建林. HDPE深水网箱抗风浪流性能的海区验证实验[J]. 海洋工程，2007，25(2)：84－90，97.

Wu Changwen, Zhu Aiyi, Shen Jianlin. Experiment on validating the capability of HDPE offshore cage to go against wind, wave and current in the sea[J]. The Ocean Engineering, 2007, 25(2): 84－90, 97. (in Chinese with English abstract)

[9] Kristiansen T, Faltinsen O M. Experimental and numerical study of an aquaculture net cage with floater in waves and current[J]. Journal of Fluids and Structures, 2015, 54: 1－26.

[10] Kristiansen T, Faltinsen O M. Modelling of current loads on aquaculture net cages[J]. Journal of Fluids and Structures, 2012, 34(4): 218－235.

[11] Fredriksson D W, Decew J C, Tsukrov I. Development of structural modeling techniques for evaluating HDPE plastic net pens used in marine aquaculture[J]. Ocean Engineering, 2007, 34(16): 2124－2137.

[12] 王笛清. 重力式网箱浮架结构变形-应力特性有限元分析[D]. 大连：大连理工大学，2014.

Wang Diqing. Finite Element Analysis on the Stress - Deformation Features of Gravity Cage Flotation Structures[D]. Dalian: Dalian University of Technology, 2014. (in Chinese with English abstract)

[13] Fredriksson D W, DeCewb J, Lader P, et al. A finite element modeling technique for an aquaculture net with laboratory measurement comparisons[J]. Ocean Engineering, 2014, 83(6): 99－110.

[14] 鄢奉林，郭根喜，何真，等. 圆形网箱浮架结构有限元分析[J]. 广东海洋大学学报，2011，31(4)：69－74.

Yan Fenglin, Guo Genxi, He Zhen, et al. Finite element analysis of circular net cage flotation structures[J]. Journal of Guangdong Ocean University, 2011, 31(4): 69－74. (in Chinese with English abstract)

[15] Wu C W, Gui F K, Li Y C, et al. Hydrodynamic coefficients of a simplified floating system of gravity cage in waves[J]. Journal of Zhejiang University SCIENCE A, 2008, 9(5): 654－663.

[16] Dong G H, Hao S H, Zong Z, et al. A theoretical analysis of dynamic elastic response of a circular ring to water waves[J]. Journal of Offshore Mechanics and Arctic Engineering, 2007, 129(3): 211－218.

[17] Tang H J, Huang C C, Chen W M. Dynamics of dual pontoon floating structure for cage aquaculture in a two-dimensional numerical wave tank[J]. Journal of Fluids and Structures, 2011, 27(7): 918－936.

[18] 黄六一. HDPE圆形双浮管网箱系统水动力学特性研究[D]. 青岛：中国海洋大学，2013.

Huang Liuyi. Study on Hydrodynamic Characteristics of Circular HDPE Sea Cage System with Double Floating Tubes[D]. Qingdao: Ocean University of China, 2013. (in Chinese with English abstract)

[19] 黄小华，郭根喜，胡昱，等. 波浪作用下圆形网箱浮架系统的运动特性分析[J]. 水产学报，2009，33(5)：878－884.

Huang Xiaohua, Guo Genxi, Hu Yu, et al. Movement characteristics of floating circular collar of net cages subjected to waves[J]. Journal of Fisheries of China, 2009, 33(5): 878－884. (in Chinese with English abstract)

[20] 黄小华，郭根喜，胡昱，等. 圆形网箱浮架系统的受力特性研究[J]. 南方水产，2009，5(4)：36－40.

Huang Xiaohua, Guo Genxi, Hu Yu, et al. Forces on floating circular collar of net cages subjected to waves[J]. South China Fisheries Science, 2009, 5(4): 36－40. (in Chinese with English abstract)

[21] 郑艳娜，董国海，桂福坤，等. 圆形重力式网箱浮架结构在波浪作用下的运动响应[J]. 工程力学，2006，23(增刊1)：222－228.

Zheng Yanna, Dong Guohai, Du Fukun, et al. Movement response of floating circle collars of gravity cages subjected to waves[J]. Engineering Mechanics, 2006, 23(Supp.1): 222－228. (in Chinese with English abstract)

[22] Shainee M, DeCew J, Leira B J, et al. Numerical simulation of a self-submersible SPM cage system in regular waves with following currents[J]. Aquacultural Engineering, 2013, 54(3): 29－37.

[23] Zhao Y P, Wang X X, Decew J, et al. Comparative study of two approaches to model the offshore fish cages[J]. China Ocean Engineering, 2015, 29(3): 459－472.

[24] Fredriksson D W, Swift M R, Irish J D, et al. Fish cage and mooring system dynamics using physical and numerical models with field measurements[J]. Aquacultural Engineering, 2003, 27(2): 117－146.

[25] 姚晓杰. 小尺度浮管结构水动力特性研究[D]. 舟山：浙江海洋学院，2015.

Yao Xiaojie. Hydrodynamic Behaviors of Small Scale Floating Tube[D]. Zhoushan: Zhejiang Ocean University, 2015. (in Chinese with English abstract)

[26] 宋瑞银，周敏珑，李越，等. 深海网箱养殖装备关键技术研究进展[J]. 机械工程师，2015，10：134－138.

Song Ruiyin, Zhou Minlong, Li Yue, et al. Development and prospect of open-sea cage equipment engineering[J]. MechanicalEngineers, 2015, 10: 134－138. (in Chinese with English abstract)

[27] Klebert P, Lader P, Gansel L, et al. Hydrodynamic interactions on net panel and aquaculture fish cages: A review[J]. Ocean Engineering, 2013, 58(4): 260－274.

[28] 中华人民共和国国家质量监督检验检疫总局. GB/T 13663.2-2005给水用聚乙烯(PE)管道系统第2部分：管件[S]. 北京：中国标准出版社，2005.

[29] 中华人民共和国国家质量监督检验检疫总局. GB/T 1040.1-2006塑料拉伸性能的测定第1部分：总则[S]. 北京：中国标准出版社，2006.

[30] 中国石油和化学工业联合会. GB/T 1041-2008塑料压缩性能的测定[S]. 北京：中国标准出版社，2008.

[31] 中国石油和化学工业联合会. GB/T 9341-2008塑料弯曲性能的测定[S]. 北京：中国标准出版社，2008.

[32] Huang Y C, Huang S C, Meng P J, et al. Influence of strong monsoon winds on the water quality around a marine cage-culture zone in a shallow and semi-enclosed bay in Taiwan[J]. Marine Pollution Bulletin. 2012, 64(4): 851－860.

[33] 关长涛，陆光炯，林德芳，等. 圆形网箱框架用PE管材的弯曲疲劳试验[J]. 中国海洋大学学报，2006，36(2)：236－240.

Guan Changtao, Lu Guangjong, Lin Defang, et al. Bending fatigue test on PE pipes used for circular cage floating collars[J]. Periodical of Ocean University of China, 2006, 36(2): 236－240. (in Chinese with English abstract)

[34] 赵建玉，王旭东，何芳，等. 电液伺服疲劳试验机的计算机控制研究[J]. 仪器仪表学报，2002，23(3)：320－323.

Zhao Jianyu, Wang Xudong, He Fang, et al. Study on computer control of the electro-hydraulic servo fatigue testing machine[J]. Journal of Scientific Instrument, 2002, 23(3): 320－323. (in Chinese with English abstract)

[35] 陈天华，孟昂，桂福坤. 波浪高度及方向对桩柱式围网养殖系统网片水力特性的影响[J]. 农业工程学报，2017，33(2)：245－251.

Chen Tianhua, Meng Ang, Gui Fukun. Effect of wave height and direction on hydraulic characteristics of net of pile-column type net enclosure aquaculture system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 245－251. (in Chinese with English abstract)

[36] 李晶. 多链聚乙烯单轴拉伸形变过程的Monte Carlo模拟[D]. 上海：复旦大学，2006.

Li Jing. The Monte Carlo Simulation of Multi-Chain Polyethylene Uniaxial Tensile Deformation Process[D]. Shanghai: Fudan University, 2006. (in Chinese with English abstract)

[37] 黄小华，郭根喜，陶启友，等. HDPE圆形重力式网箱受力变形特性的数值模拟[J]. 南方水产科学，2013，9(5)： 126－131.

Huang Xiaohua, Guo Genxi, Tao Qiyou, et al. Numerical simulation of the forces and deformation of HDPE circular gravity cages[J]. South China Fisheries Science, 2013, 9(5): 126－131. (in Chinese with English abstract)

[38] 机械设计手册编委会. 机械设计手册：第1卷[M]. 3版.北京：机械工业出版社，2007.

[39] 董晓传. 大型液压机组合部件的临界预紧力研究[D]. 秦皇岛：燕山大学，2014.

Dong Xiaochuan. Study on Critical Preload of Prestressed Composite Structures of Large Hydraulic Press[D]. Qinhuangdao: Yanshan University, 2014. (in Chinese with English abstract)

Mechanical property analysis and optimization of deep-water net cage guardrail

Liu Haiyang1,2, Wang Shaomin1,2, Huang Xiaohua1,2, Tao Qiyou1,2, Hu Yu1,2, Guo Genxi1,2※, Song Liming3

(1.,,,,,510300,; 2.,,,572018,; 3.,,201306,)

Guardrail is an indispensable component of the deep-water net cage floating system, and it plays an important role to maintain culture volume of net cage and to resist the impacts of wave and current with net cage floating system. But there are few researches on guardrail mechanical properties of deep-water net cage. In order to improve the safety of deep-water net cage structure, three-dimensional solid models of guardrail were established by software Unigraphics NX, these models were calculated by finite element method of the software ANSYS Workbench. Firstly, mechanics properties of hexagon-triangle and circle type guardrails were investigated; Secondly, the collected data in the experiment and numerical simulation were analyzed by using linear and nonlinear regression methods to understand the mechanical performance of guardrails, and finally the design of guardrail was optimized with consideration of experiment and simulation results. The results of statics test showed that for high density polyethylene (HDPE) guardrail, tensile yield strength was 23.8 MPa, Young’s modulus was 1 240 MPa, and flexural strength was 25.2 MPa. Results of finite element modal analysis indicate that natural frequency range of guardrail was 14.25-33.59 Hz; stress range was 6.370-21.658 MPa. Fatiguevibration experiment was conducted by using hydraulic servo fatigue testing machine. Vibration frequency was set as 5 Hz, and vibration amplitude was 80% maximum compressive intensity of stress value (19.6 MPa). Results of fatigue test showed that fatigue fracture time was 23.5 h. According to finite element statics analysis, the biggest, medium and smaller displacement, stress and strain of guardrail was occurred in attack angle of 0°, 45°, and 90°. The displacement, stress and strain of concentrated load was higher than those of distributed load. The guardrail failed when the concentrated load was 4 kN in attack angle of 0°, and displacement, stress and strain was 70.47 mm, 28.922 MPa, 0.026 434, respectively. The maximum displacement area was in the center of guardrail-handrail; themaximum stress areawas in thebottom of guardrail-column. When attack angle to guardrail is 0°, the column was simplified as cantilever beam model. When attack angle is 90°, handrail was simplified as the form of tension and compression bar model. Based on finite element linear analysis of circular and hexagonal handrails, handrails of circle and hexagon failed when distributed loads were 6 kN and 16 kN, respectively, and stiffness of circular handrail was greater than that of hexagon significantly. Based on finite element nonlinear analysis of circular and hexagonal handrails, HDPE material model was set up by bilinear isotropic hardening model for isotropic materials (BISO). Deviations between simulation value and experimental value of guardrail and handrail at elastic stage were 8.67% and 0.27%, respectively. Deviation between simulation data and experimental data of handrails at plastic stage was analyzed by using method of Kolmogorov–Smirnov (K-S) two - factor fitting goodnessexamination. And the examined result of hexagonal handrail was=0.861 3>0.05, namely, there is no significant difference between finite element simulation and mechanics experiment in linear and nonlinear process. The sectional rigidity of guardrail was improved by designing the cross-sectional shape of guardrail-pipe. Compared with hollow-circle section of guardrail, flexural property of hollow-oval section and hollow- square section was increased by 6.58%, 6.83% respectively, in same materials. This study provides theoretical basis for the structural and mechanical properties for guardrail system.

finite element method; mechanical properties; high density polyethylene; deep-water net cage; handrail

10.11975/j.issn.1002-6819.2017.04.034

S953.5

A

1002-6819(2017)-04-0248-10

2016-05-27

2017-02-12

中央级公益性科研院所基本科研业务费专项资金(中国水产科学研究院南海水产研究所)资助项目（2016TS14，2015TS12）；海南省重大科技计划项目（ZDKJ2016011）；国家自然科学基金资助项目（31402349）；海洋经济创新发展区域示范专项项目（GD2013-D01-001）；广东省科技计划项目（2013B020501001）

刘海阳，男，硕士，从事渔业设施工程技术与装备研究。广州 中国水产科学研究院南海水产研究所，510300。Email：18818399534@139.com

郭根喜，男，研究员，从事设施渔业研究。广州 中国水产科学研究院南海水产研究所，510300。Email：scsggx@163.com

刘海阳，王绍敏，黄小华，陶启友，胡 昱，郭根喜，宋利明. 深水网箱护栏力学性能分析及优化[J]. 农业工程学报，2017，33(4)：248－257. doi：10.11975/j.issn.1002-6819.2017.04.034 http://www.tcsae.org

Liu Haiyang, Wang Shaomin, Huang Xiaohua, Tao Qiyou, Hu Yu, Guo Genxi, Song Liming. Mechanical property analysis and optimization of deep-water net cage guardrail[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 248－257. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.04.034 http://www.tcsae.org