一种改进的多分量正弦调频信号时频分析算法

吕 军， 贠乐应， 牛敏杰

(陆军装甲兵学院信息工程系，北京 100072)

自然界中的信号可按照频率是否随时间线性变化分为线性调频(Linear Frequency Modulation, LFM)信号和非线性调频(Non-Linear Frequency Modulation, NLFM)信号[1]，其中正弦调频(Sinusoidal Frequency Modulation, SFM)信号是一种常见的非线性调频信号，广泛存在于无线通信等诸多领域，对这类信号进行分析具有重要的意义。如：目标微运动引起的雷达回波信号就是一种典型的SFM信号，对这类信号进行分析可为雷达目标微多普勒特征提取奠定基础[2]。

由于频率特性是信号的重要特性，其中蕴含着很多信号特征，因此有必要对SFM信号的频率特性进行分析。但是SFM信号的频率随时间呈正弦形式变化，属于频谱时变信号，采用传统的傅里叶变换无法很好地描述其频率的变化规律，需采用时频分析方法[3]。

现有的时频分析方法主要有短时傅里叶变换(Short-Time Fourier Transform, STFT)、魏格纳分布(Wigner-Ville Distribution, WVD)、平滑伪魏格纳分布(Smoothed Pseudo WVD, SPWVD)、重排平滑伪魏格纳分布(Reassigned SPWVD, RSPWVD)等[4]，其中：STFT的性能受窗函数的影响较大，当窗函数较短时，时域分辨率高，频域分辨率低，反之，频域分辨率高，时域分辨率低，但是没有交叉项的干扰；WVD具有较高的时频分辨率，但是交叉项干扰严重；SPWVD通过加窗减少了交叉项干扰，但是同时也降低了时频分辨率；RSPWVD通过对SPWVD时频分布进行重排，大幅度减少了SPWVD中的交叉项干扰，同时提高了时频分辨率，但是计算复杂度较高，实时性差[5]。

基于以上问题，为了获得一种时频分辨率高、交叉项干扰抑制强、运算量低以及更接近于真实结果的时频分析算法，笔者基于STFT和WVD的优点，提出一种改进的STFT-WVD时频分析算法，并通过仿真分析验证该算法的有效性。

1 SFM信号分析

SFM信号可统一表示为[6]

x(t)=Aexp[jφ(t)]=

Aexp[j2πfct+jmfsin(2πfmt)],

(1)

式中：0≤t≤T；A为信号的幅度；fc为载频；fm为调制频率；mf为调制指数。

对信号的相位项关于时间求导，可推导出SFM信号的频率为

(2)

式中：mffm为调制频偏，即Δf。则可得SFM信号理论时频特性如图1所示。

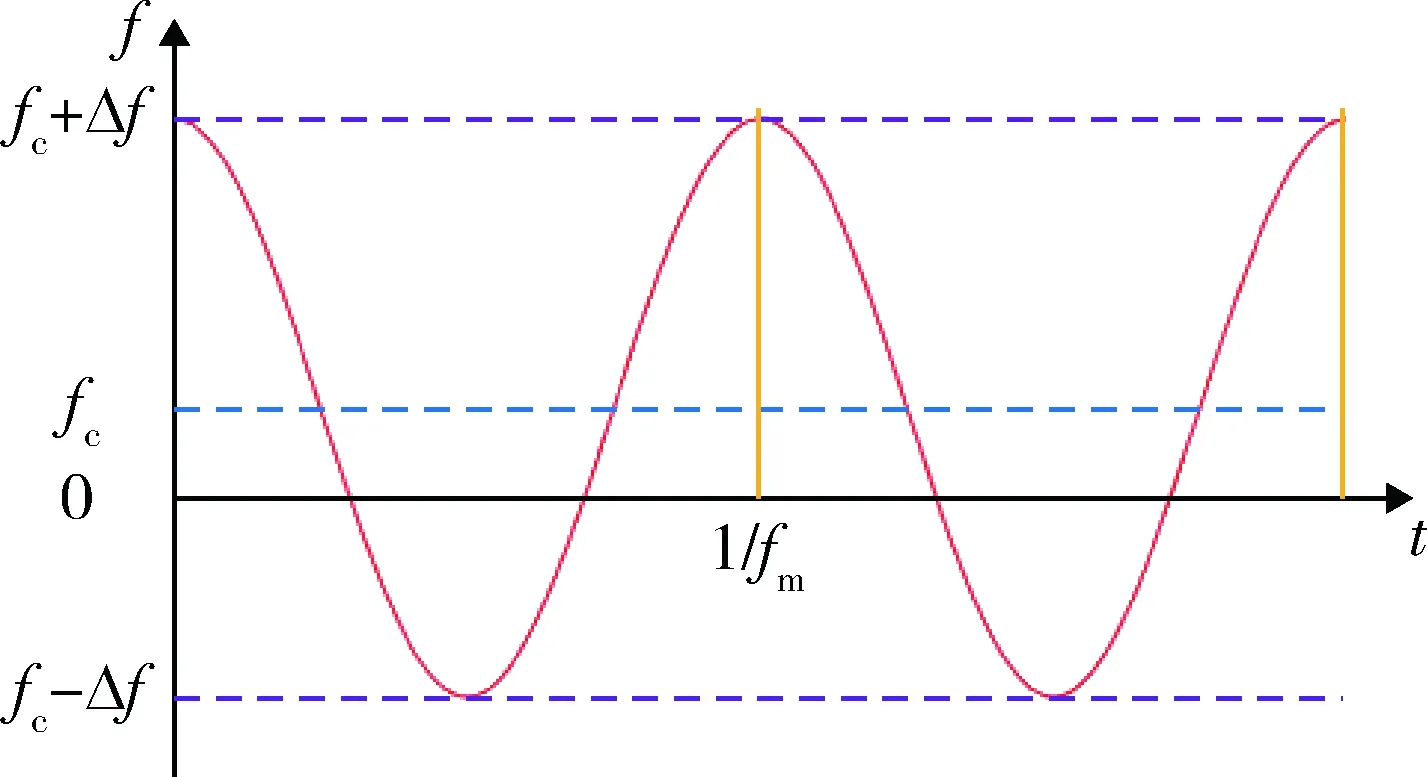
图1 SFM信号理论时频特性

由图1可知：SFM信号的频率以载频fc为中心轴随时间呈正弦形式变化，其幅度为Δf，信号频率的变化周期为1/fm。

由式(1)可得：N个分量SFM信号的模型为

(3)

同理，可得其时频特性为多个频率随时间呈正弦形式变化的曲线，每个分量曲线的中心轴线不同，与载频fci相关；初始频率也不同，与各分量的调制频偏Δfi相关。

2 改进的STFT-WVD时频分析算法

王见等[7]给出了一种STFT-WVD算法的定义：对信号的STFT谱设立阈值，当STFT谱的值小于该阈值时，令谱值为0，当STFT谱的值大于该阈值时，令谱值为1，得到新的矩阵，将该矩阵与WVD矩阵相乘，得到新的时频分布。此时，WVD中交叉项部分对应的谱值均变为0。其定义式为

Vx(t,f)=Wx(t,f){|Sx(t,f)|>c}，

(4)

式中：c为阈值；Wx(t,f)为信号的WVD变换所得矩阵；Sx(t,f)为信号的STFT变换所得矩阵。由定义可知：该方法所得时频分布的时频分辨率会得到一定提高，同时交叉项干扰也得到了抑制。

由式(3)可知: 对于多分量SFM信号，在同一时间，不同分量信号的频率会有相等的情况，对这类信号采用STFT算法进行时频分析后，由于STFT谱时频分辨率差，在频率相等的地方容易形成模糊的区域，采用STFT-WVD算法进行时频分析后，这一区域仍然存在，所得时频分布的性能仍有待提高[8]。

为了在较短时间内实现对多分量SFM信号时频特性的分析，笔者提出一种改进的STFT-WVD时频分析算法，主要思想为：通过对STFT矩阵和WVD矩阵的乘积矩阵设立阈值来改善时频分布性能，对2类矩阵求积之后，STFT谱中的模糊区域以及WVD谱中的交叉项部分保持不变，但信号的自项部分得到了加强，此时再设立阈值进行后续分析，得到的时频分布的性能必将优于直接使用STFT-WVD算法所得。改进的STFT-WVD算法定义式为

Dx(t,f)=Wx(t,f)×

(5)

式中：a为幂调节系数。

改进的STFT-WVD算法具体步骤如下：

1)对信号y(t)进行STFT变换和WVD变换,分别得Sx(t,f)和Wx(t,f)；

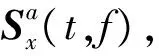
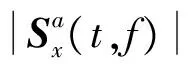
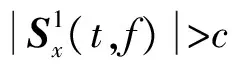
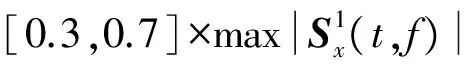
3 仿真分析

为了检验改进的STFF-WVD算法对多分量SFM信号进行时频分析的效果，笔者进行了仿真分析。假设y(t)为具有6个分量(i=1,2,…,6)的SFM信号，其信号幅度Ai=1，载频fci=1100Hz，信

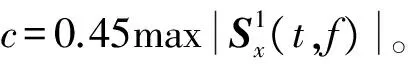
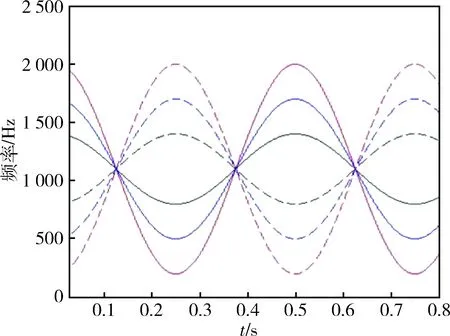
图2 多分量SFM信号理论时频特性

分析图2、3可以看出：1) STFT、WVD、SPWVD、RSPWVD、STFT-WVD及改进的STFT-WVD算法所得的时频分布变化规律与理论推导所得一致，验证了理论分析的正确性和改进算法的有效性；2) STFT算法时频分辨率较低，WVD算法时频分布自项部分完全淹没在交叉项中，SPWVD、RSPWVD和STFT-WVD算法时频分布在不同分量频率相等处均出现频率特征丢失或者改变的情况；3)改进的STFT-WVD算法时频分辨率较高，交叉项干扰少，同时与STFT-WVD算法相比，在不同分量频率相等处特征丢失较少。

为了对比不同算法的复杂度，笔者对不同算法完成多分量SFM信号时频分析耗时进行了对比，结果如表1所示。可以看出：对多分量SFM信号的时频分析中，RSPWVD算法耗时最多，SPWVD算法次之，其余4种算法耗时较少，均低于0.5 s。因此，在实时性要求较高的多分量SFM信号时频分析中，RSPWVD和SPWVD算法不再适用，而改进的STFT-WVD算法则可满足实时变换的要求。

表1 不同算法时频分析耗时对比

为了检验改进的STFT-WVD算法的抗噪能力，分别对上述仿真信号加入-5、0、5 dB高斯白噪声进行时频分析，并与STFT、STFT-WVD算法的时频分析结果进行对比，分别如图4-6所示。

图4 信噪比为-5 dB时不同算法时频分析结果对比

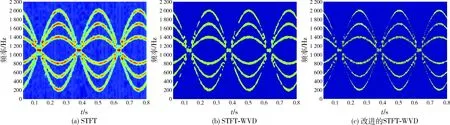
图5 信噪比为0 dB时不同算法时频分析结果对比

图6 信噪比为5 dB时不同算法时频分析结果对比

对比分析图4-6可知：1)STFT算法对噪声极其敏感，信噪比越小，时频分析效果越差；2)STFT-WVD和改进的STFT-WVD算法对噪声都不太敏感，但是改进的STFT-WVD算法性能更优，在信噪比较低的情况下，仍能获得时频分辨率较高、特征丢失较少的时频分布，具有良好的抗噪能力。

4 结论

时频分析作为研究非线性、非平稳信号的主要手段，已成为公认的有效方法，但没有适合所有信号的通用时频分析方法。本文从多分量SFM信号的时频分析方法出发，提出了一种改进的STFT-WVD时频分析算法。理论和仿真分析结果表明：与STFT-WVD算法相比，改进算法保留了原算法在时频分辨率、交叉项干扰抑制和运算量等方面的优点，但在不同分量频率曲线交叉区域特征丢失较少，验证了改进算法对多分量SFM信号处理的有效性。

[1] 陈晶.线性调频信号与正弦调频信号参数估计方法[D].哈尔滨：哈尔滨工程大学，2012.

[2] CHEN V C.Micro-Doppler effect in radar phenomenon,model and simulation study[J].IEEE transactions on aerospace and electronic systems,2006,42(1):2-21.

[3] 邹红星,周小波,李衍达.时频分析:回溯与前瞻[J].电子学报,2000,28(9):78-84.

[4] 王炳和.现代数字信号处理[M].西安：西安电子科技大学出版社，2011：351.

[5] 陈超，郝雁中，高宪军，等.基于WVD改进算法的跳频信号参数估计[J].海军工程大学学报,2011,23(6):91-95.

[6] 朱航，张淑宁，赵慧昌. 基于广义周期性的单通道多分量正弦调频信号分离和参数估计[J].电子与信息学报,2014,36(10):2438-2444.

[7] 王见,李金同,卢华玲，等.采用STFT-Wigner变换抑制Wig-ner-Ville分布交叉项[J].重庆大学学报，2013，36(8)：15-18,25.

[8] 葛哲学，陈仲生.MATLAB时频分析技术及其应用[M].北京：人民邮电出版社，2006：16.

[9] 张纳温，李树彬，李松，等. 基于STFT-WVD联合的认知无线电频谱感知分析与仿真[J]. 吉林大学学报，2010，28(2)：124-130.