基于自抗扰算法的“动中通”系统控制策略

陆 叶，邓桐彬，蒋忠伟，陶慧敏

(中国电子科技集团公司第二十八研究所，南京 210001)

基于自抗扰算法的“动中通”系统控制策略

陆 叶，邓桐彬，蒋忠伟，陶慧敏

(中国电子科技集团公司第二十八研究所，南京 210001)

“动中通”(SOTM)伺服控制系统通常采用三闭环PID控制策略进行控制器的设计;然而，由于系统扰动和系统时变性参数的存在，传统PID算法难以保证“动中通”系统稳定、可靠地工作;针对传统控制策略的弊端，建立了“动中通”系统数学模型，并提出了一种基于自抗扰(ADRC)算法的双闭环控制策略;仿真实验表明，基于ADRC的双闭环控制策略不仅具有更快的响应速度和更高的控制精度，还有更强的鲁棒性，能有效地弱化系统扰动的影响，满足“动中通”系统的功能需求。

动中通；自抗扰；伺服控制系统

0 引言

“动中通”(SOTM)是一种在运动状态下利用通讯卫星传递话音、数据、图像及其他信息的重要通信技术，由于其抗干扰能力强，保密性能好，通信距离远的特点，“动中通”系统在军事指控系统中得到了广泛应用。为了能在运动过程中保持精准的对星，“动中通”系统要求建立一个响应速度快、控制精度高、鲁棒性好的伺服控制系统，目前“动中通”系统的控制主要采用PID控制、超前之后控制等传统控制算法[1]。但是，考虑到在“动中通”系统对星过程中参数时变性的影响，传统的控制算法很难满足“动中通”系统的要求[2]。另一方面，由于军事作业的特殊性，要求“动中通”系统能在各种复杂恶劣的路况下正常工作，对系统鲁棒性提出了极高的要求，针对传统控制算法的弊端，本文提出了一种基于ADRC控制算法的双闭环控制策略，并在MATLAB/Simulink环境下进行仿真实验。仿真结果表明，本文提出的控制策略能对“动中通”系统实现精确控制，不仅具有快速的响应速度和较高的控制精度，还具有较强的鲁棒性，能有效地弱化外部扰动和时变性参数对系统的负面影响。

1 系统分析与建模

基于仿真实验的要求，本文在实验室环境下搭建了“动中通”系统，其机械结构如图1所示。

图1 “动中通”系统机械结构

“动中通”系统主要由卫星天线和二自由度转台组成。转台由俯仰轴和横滚轴两个轴系构成，两轴系彼此正交，无耦合关系，可在电机驱动下独立工作。卫星天线固定于转台上，通过调整转台俯仰角和横滚角，即可实现“动中通”系统的姿态控制，以达到对星目的[3-4]，其主要技术参数如表1所示。

表1 “动中通”转台主要参数

系统硬件电路总体结构框图如图2所示。

图2 系统硬件电路总体结构框图

其中系统以微处理器作为控制器的核心，以FAULHABER公司的3863碳刷直流电机为执行元件，另外配有GPS定位系统、倾角传感器用于采集系统当前位置信息和姿态信息。其中控制器通过RS232与GPS定位系统相连，获取当前地理位置信息。“动中通”系统的姿态信息由倾角传感器测得病送至控制器。控制器根据测得信息分析计算，并发送PWM指令驱动电机，通过姿态校正的方式跟踪卫星，实现对“动中通”系统的闭环控制。

为简化研究对象，“动中通”系统可解耦为两个单自由度(俯仰、横滚)转台，在对单自由度“动中通”系统各组成环节进行线性化分析的基础上，本文建立了“动中通”系统数学模型。考虑到“动中通”系统由转台负载和电机组成，负载与电机之间可视为纯刚性链接，两者之间阻尼效应和弹性效应可以忽略[5]。因此，单自由度“动中通”系统可用图3表示[6]。

图3 “动中通”系统原理图

图中参数如下所示：

Ua为电枢电压；La为电枢电感；Ra为电枢绕组；E为反电动势；Te为电磁转矩；Tl为负载转矩。

根据图3分析可得，系统平衡方程如下：

电机动力学平衡方程：

(1)

其中：J为转动惯量；ω为转动角速度。

电机电枢电压平衡方程：

(2)

式(2)经Laplace变换可得：

(3)

其中：τ1为电磁时间常数。

根据电机电磁转矩和电枢反电势可表示为：

(4)

其中：Cm为电磁转矩常数；Ce为电势常数。

式(4)代入式(1)可得：

(5)

Idl为等效负载电流。

经Laplace变换后可得：

(6)

其中：τm为机电时间常数。

根据以上分析，“动中通”系统传递函数为式(3)、式(6)，可简化为一个二阶模型，其系统框图如图4所示。

图4 “动中通”系统框图

根据第1章分析可知，在“动中通”工作过程中，负载转矩随卫星天线的转动而改变，考虑到参数时变性的影响，传统PID算法难以满足系统工作的稳定性和可靠性。在第2章中，本文研究了自抗扰(ADRC)控制算法，并将其应用到“动中通”伺服控制系统中。

2 控制器设计

自抗扰(ADRC)控制是一种不依赖于被控系统精确数学模型的非线性控制器，它将时变性参数的影响和系统外部扰动作为控制系统的总扰动[7]，并进行扰动观测和扰动补偿。相比于传统PID控制器，本文研究的自抗扰控制器具有更高的控制精度和更强的鲁棒性[8-9]，其基本结构如图5所示。

图5 ADRC控制器基本结构

2.1 自抗扰理论

如图5所示，自抗扰控制器可分为3个模块，跟踪微分器(TD)，扩展状态观测器(ESO)，非线性控制率(NLSEF)[10]。

(1)跟踪微分器(TD)。

跟踪微分器用于跟踪输入信号并预测输入信号的变化趋势，可有效地减小系统初始误差，若参数设计合理，可使系统无超调地进入稳态，其数学表达式为：

(7)

其中：h为积分步长；r为上升时间常数；fst为非线性函数。

(2)扩展状态观测器(ESO)。

扩展状态观测器是自抗扰控制器的核心部分，可用于估计系统状态、模型和外部扰动，从而提高控制系统的精确性和鲁棒性，其数学表达式为：

(8)

其中：

Zi为扩展状态观测器输出；y为系统输出；β1i为观测器系数；u为系统控制输入；b0为系统控制系数。

(3)非线性控制率(NLSEF)。

非线性控制率针对扩展状态观测器反馈的被控对象状态给出控制信号针对外部扰动的实时作用量而给以补偿，其数学表达式为：

(9)

其中：ei为误差输入；β2i为状态反馈系数；uo为控制器输出。

2.2 系统结构

“动中通”伺服控制系统通常采用三闭环PID控制，由于负载时变性的影响，PID参数需要实时在线调整，不仅参数配置十分麻烦，而且很难保证系统的稳定性和可靠性[11-12]。针对三闭环PID控制策略的弊端，本文设计了一种基于自抗扰算法的双闭环控制策略，其系统框图如图6。

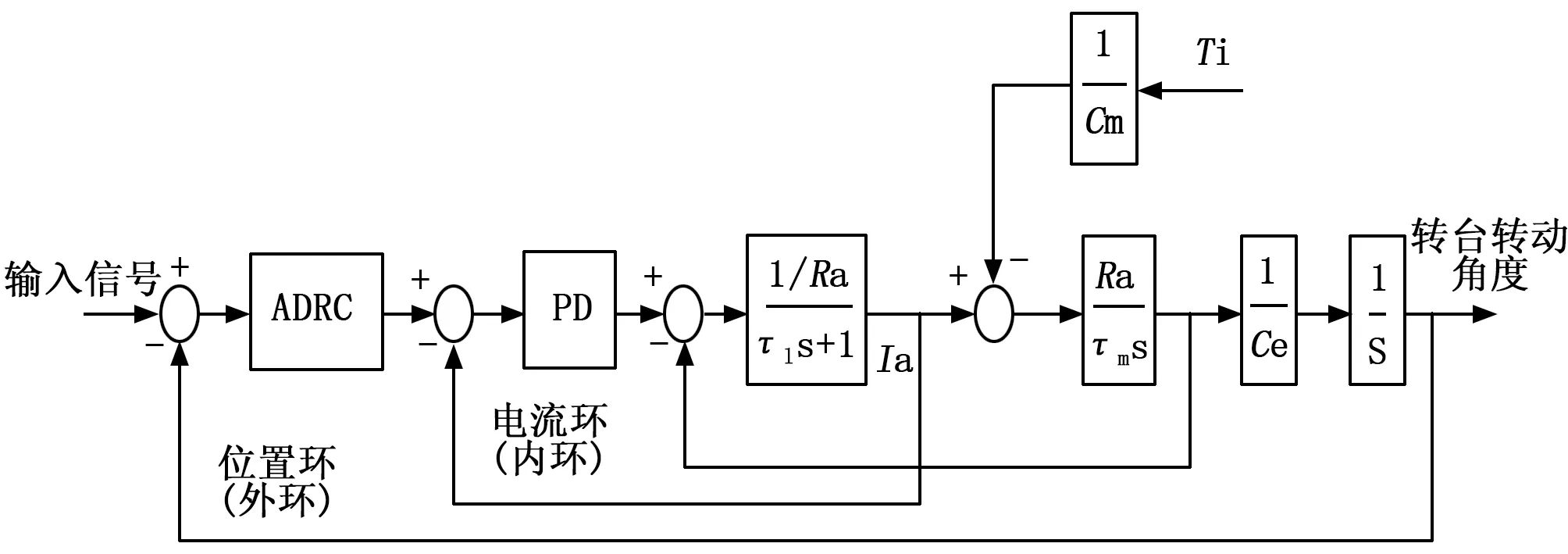
图6 控制系统系统结构图

如图6所示，控制系统由电流环和位置环组成双闭环控制系统，内环(电流环)用于提高系统响应速度，采用PID控制器设计；外环(位置环)采用ADRC控制器设计，用于“动中通”系统的姿态控制，并提高系统的鲁棒性，弱化时变性参数和外部扰动对系统的影响。仿真结果表明，相比于传统PID三闭环控制策略，基于自抗扰控制算法的双闭环控制策略不仅简化了系统结构，降低了参数配置的复杂度，而且极大地提高了系统控制精度和鲁棒性。

3 仿真实验

为验证ADRC双闭环控制策略的有效性，本文在MATLAB/Simulink环境下进行了仿真试验。

3.1 阶跃响应实验

给“动中通”系统输入30°或 -30°的阶跃控制信号，观察在两种不同控制策略下的系统响应曲线。

如图7所示，在ADRC双闭环控制策略的控制下，系统超调量远远小于传统PID控制策略，同时，系统阶跃响应上升时间约为0.2秒，而在PID控制策略下系统阶跃响应时间为2秒。因而，对于“动中通”系统，本文提出的ADRC双闭环控制策略的控制性能明显优于传统PID控制策略。

图7 阶跃响应实验

3.2 抗扰动仿真实验

考虑到“动中通”系统多通常工作在恶劣的环境下，因此鲁棒性是检验其控制系统性能的重要指标。在MATLAB/Simulink环境下控制系统转轴转动30°，给系统施加在0～1Nm范围内变化的扰动转矩，两种不同控制策略下的系统响应曲线如图8所示。

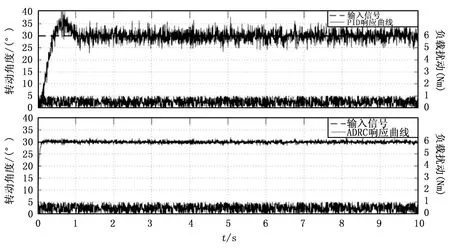
图8 抗扰动仿真实验

如图8所示，采用PID控制策略的动中通系统受外部扰动影响严重，其转轴最大角度误差高达5°。相比于传统PID控制策略，本文提出的ADRC双闭环控制策略几乎不受外部扰动影响，具有更强的鲁棒性。

4 结论

仿真实验结果证明了本文提出的ADRC控制策略具有优秀的控制性能和极强的鲁棒性。事实上，ADRC控制策略不仅适用于单自由度“动中通”系统，还能应用于各种复杂的多阶系统。仿真试验表明，相比于传统的PID控制策略，ADRC控制策略具有以下特性：

(1)减小了系统超调量，提高了系统响应速度。相比于PID控制策略，ADRC控制策略表现出更好的静、动态特性。

(2)通过扩展状态观测器实时观测时变性参数和外部环境扰动的负面影响，并通过控制算法予以补偿，极大地提高了系统的鲁棒性。

[1] 田 华.船载“动中通”定向天线控制系统的研究与开发[D].西安：西安电子科技大学,2008.

[2]JamesDebruin.EstablishingandMaintainingHigh-bandwidthSatelliteLinksDuringVehicleMotion[J].IEEEcontrolmagazine, 2008, 28(1): 93-101.

[3]XuH,YaoM,ShenX.Studyonbasicprinciplesoftri-axialstabilizationforflatSOTMonvehicle[J].SystemSimulationandScientificComputing. 2008,47(2):1104-1109.

[4] 杜江鹏.基于三轴自助跟踪平台的研究与实现[D].南京：南京理工大学,2010.

[5] 钱 健,王维亚. 无刷直流电机模型的建立及控制系统仿真研究[J].广西大学学报(自然科学版),1995,20(1):73-77.

[6]YuXH,ManZH.FastterminalslidingmodecontroldesignforNonlinearDynamicalSystems[J].IEEEtransactiononCircuitsandSystems:FundamentalTheoryandApplications, 2002, 49(2): 262-264.

[7] 韩京清，自抗扰控制技术：估计补偿不确定因素的控制技术[M].北京：国防工业出版社,2008.

[8] 韩京清. 非线性状态误差反馈控制律──NLSEF[J]. 控制与决策, 1995(3).

[9] 孟凡东.自抗扰控制器的设计与应用研究[D]. 哈尔滨：哈尔滨理工大学,2009.

[10]HikertJM.InertiallyStabilizedPlatformTechnology[J].IEEEControlSystemsMagazine, 2008,28(1): 26-46.

[11]LureAI,PostnikovVN.Onthetheoryofstabilityofcontrolsystems[J].Appliedmathematicsandmechanics,2005,8(3).

[12]HanJingqing.FromPIDtoActiveDisturbanceRejectionControl[J].IndustrialElectronics, 2009, 56(3): 900-906.

An Active Disturbance Rejection Control Strategy for SOTM Servo Control System

Lu Ye, Deng Tongbin, Jiang Zhongwei, Tao Huimin

(28thResearch Institute, China Electronics Technology Group Corporation,Nanjing 210001,China)

Satcom-on-the-Move (SOTM) servo control system is usually designed as a three closed-loop system with PID algorithm. However, traditional PID algorithm can hardly meet the requirements of SOTM servo control system because of the influences from the time-varying property of the parameters and the disturbance. In this paper, a mathematical model of SOTM system is depicted and a dual closed-loop system with active disturbance rejection control (ADRC) algorithm is proposed. Compared with the traditional PID algorithm, the proposed algorithm has many advantages, such as faster response and higher precision, robustness to the influence of the load disturbance, etc.. The simulating results have verified these advantages.

SOTM；ADRC；servo control system

2016-09-03；

2016-11-02。

陆 叶(1989-)，男，江苏南通人，助理工程师，主要从事系统集成方向的研究。

1671-4598(2017)03-0063-04

10.16526/j.cnki.11-4762/tp.2017.03.018

TP273

A