温度约束的MEMS陀螺零漂补偿模型
阎歆婕,林 宇,李 建,张 晋,林丹丹
温度约束的MEMS陀螺零漂补偿模型
阎歆婕,林 宇,李 建,张 晋,林丹丹
(昆明物理研究所,云南 昆明 650223)
针对现有MEMS零位随机漂移的缺陷,本文建立关于温度约束的确定性模型MEMS陀螺零位漂移补偿模型。首先,依据MEMS陀螺信号的测量模型,将陀螺信号误差分解为确定性误差和随机性误差,针对由温度引入的确定性误差,建立温度-零偏和温度-主频率分量确定性约束模型,有效消除信号序列中的温度引入趋势项和辨识周期项;其次,利用自回归滑动平均模型(Auto-Regressive and Moving Average Model,简称为ARMA模型)逼近MEMS陀螺信号中的随机误差项,准确地预测出随机误差的变化趋势;最后,采用Kalman滤波优化ARMA模型的预测效果,进一步提高模型的状态估计精度。理论分析和实验结果验证了该模型的鲁棒性和有效性。
温度约束;零漂补偿;MEMS陀螺
0 引言
随着惯性技术的发展,高性能陀螺的小型化正逐渐成为目前研究的主流。硅微机械陀螺(MEMS Gyroscope)由于体积小、重量轻且其性能指标满足一定精度级别的优点,得到业界的广泛关注。硅微机械陀螺由单晶硅片经过光刻和各向异性的刻蚀工艺制造而成,继承硅微型惯性器件的缺点,即其输出容易受自身裁量、制造工艺以及工作环境等各种因素的影响,尤其是温度所造成的影响不可忽视。在尺寸限制的组合导航、小型化稳定平台等应用中,对陀螺仪精度要求较高且有空间大小约束时,难以在矛盾的性能与体积之间取舍。为满足应用环境中对陀螺尺寸和性能双需求,必须采用可行方法有效提高MEMS陀螺的精度,补偿其漂移。
由于环境温度的影响,MEMS陀螺仪自身材料特性和其外围电路的电气特性都会随温度的变化而变化,并带来影响陀螺性能的热噪声[1],进而影响到陀螺的零位输出和标度因数,导致MEMS陀螺仪的输出精度低和稳定性差。
近年来,关于MEMS陀螺随机漂移的研究得到广泛关注并取得一定进展。Igor P. Prikhodk等[2]提出一种基于自感应实时温度值的高品质因数速率MEMS陀螺零位漂移补偿算法;在研究基于MEMS陀螺的计算机先进鼠标系统中,杜家英[3]对比高通滤波器、经典Kalman滤波、最小均方根原则的LMS自适应滤波3种方法对MEMS陀螺信号的处理效果,验证Kalman滤波的效果最佳;针对光电稳定平台的性能受陀螺速率精度影响的问题,国防科大的朱华征[4]对比数字低通滤波、最优小波阈值滤波和Kalman滤波3种方法,分析每种方法的优点和局限性,建立MEMS陀螺随机漂移的ARMA模型,以Allan方差与功率谱相结合的方法分析陀螺随机漂移的补偿效果,有效地提高稳定平台精度。上海交大的王昊等[5]详细分析陀螺信号随机漂移的非平稳性,利用梯度径向基(RBF)神经网络对陀螺随机漂移建模。李士心[6]针对MEMS陀螺的零偏随温度非线性变化的情况,提出一种基于灰色模型和RBF神经网络结合的零偏温度补偿方法。时间序列分析法及ARMA模型[3-4,7]在陀螺信号处理中较为常用,而神经网络和小波分析[8]等方法由于受硬件平台的计算能力所限,可能会产生复杂的计算量,导致补偿延时的问题。
针对MEMS陀螺零位温度漂移的问题,本文建立一种温度约束的MEMS陀螺零位漂移补偿模型。首先,通过采集到的实验数据对温度引入的确定性误差建模,消除信号序列中的温度引入的趋势项和利用温度电压辨识周期项。其次,在处理后的数据通过平稳性检验后,利用ARMA模型模拟MEMS陀螺信号中的随机漂移,预测出随机误差的变化趋势。最后借助经典Kalman滤波的最优线性预测效果优化ARMA模型的预测性能,进一步提高模型的状态估计精度。
1 MEMS陀螺测量模型
根据陀螺信号的特点,建立的MEMS陀螺测量误差模型[9]如式(1)所示:
=(+D)+null+Noise (1)
式中:为陀螺的输出电压;为陀螺的标度因数;为陀螺的速率值;D为陀螺标度因数误差;null为零位偏置;Noise为随机误差。其中,零偏和标度因数误差属于确定性误差,并且受环境因素的影响,如温度、振动、外场加速度等。
本文假设MEMS陀螺零位输出的影响因素之间彼此相互独立,即各因素的影响效果线形叠加,因此若分别补偿确定性误差和随机误差,便能在一定程度上提高MEMS陀螺输出的速率精度。
根据采集到的MEMS陀螺信号数据发现,零位偏置f受温度影响,且陀螺零位信号频谱分析中幅值最大的频率项也会随温度变化而不同。本文主要研究的是陀螺零漂与温度的关系,故在下面的改进公式中仅列出温度引入的相关项,见式(2)、式(3):
null=1()+2() (2)
Noise=Noise1()+Noise2(3)
式中:1()是温度引入的零位偏置趋势项;2()是与温度相关的周期项;Noise1()是温度引入的随机误差项;Noise2近似为白噪声。
2 温度约束的确定性模型
2.1 温度-零偏约束模型
MEMS陀螺在不同温度点下的静态输出的均值不同,因此本文假设陀螺的零位偏置电压是关于温度值的函数。为进一步确定温度与MEMS陀螺的零位电压输出的关系,进行实验如下。
将某型MEMS陀螺放置于温箱中,在温度范围为-40℃~60℃内每间隔10℃采集MEMS陀螺的温度和速率电压输出,令采样率为1000Hz,采集前先保温30min,采样时间为1h。取每一环境温度点下温度稳定后的全部温度、速率电压数据均值,建立陀螺零位速率与温度的关系曲线图,如图1(a)所示,每个温度点速率电压数据的方差与温度的关系如图1(b)所示。
由图1可知,随温度的增加陀螺零位速率逐渐增大,零位速率的方差也随之增大,即温度不仅影响陀螺零位输出的趋势项,也影响陀螺零位输出的随机误差。
根据图1(a)采用多项式拟合方法,建立温度模型如式(4)所示:
1()=aT+…+1+0(4)
式中:为温度;a,…,1,0为模型参数;为模型的阶数。
结合式(4),选取陀螺温度传感器输出稳定后的数据作为训练数据,以最佳曲线逼近法为原则,估计不同阶数模型的参数得到各阶次模型指标如表1所示,表示模型预测值和实际值的误差,表示模型的运算时间,以此衡量模型的计算量。
由表1可知,随着阶次的增加,误差的最大值、均方误差和、误差标准差变化趋势一致,表明未发生过拟合现象。=4时,最小误差值较小,但不影响总体趋势,可能为偶然因素导致。值从4变化到5时各指标变化较大。结合不同阶次模型的计算量,本文选取=5。
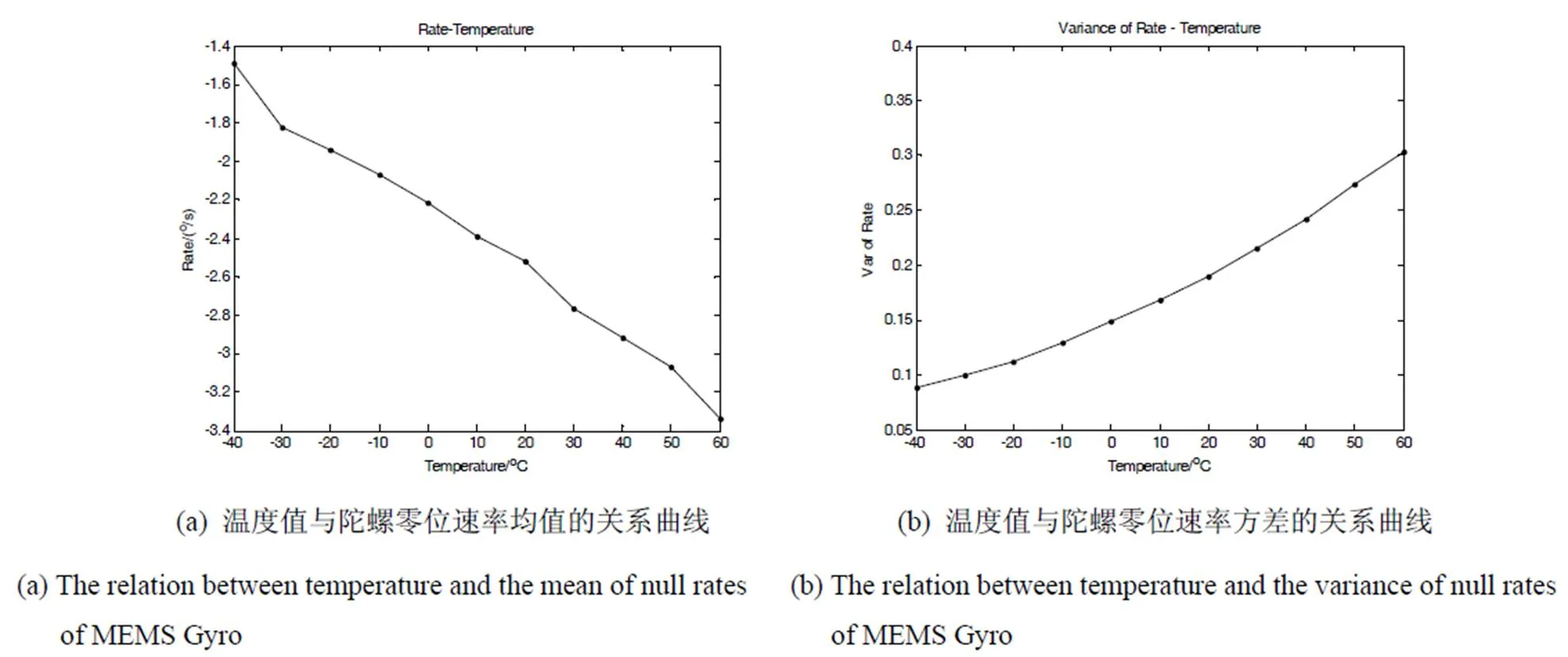
图1 温度值与陀螺零位速率输出均值及其方差的关系
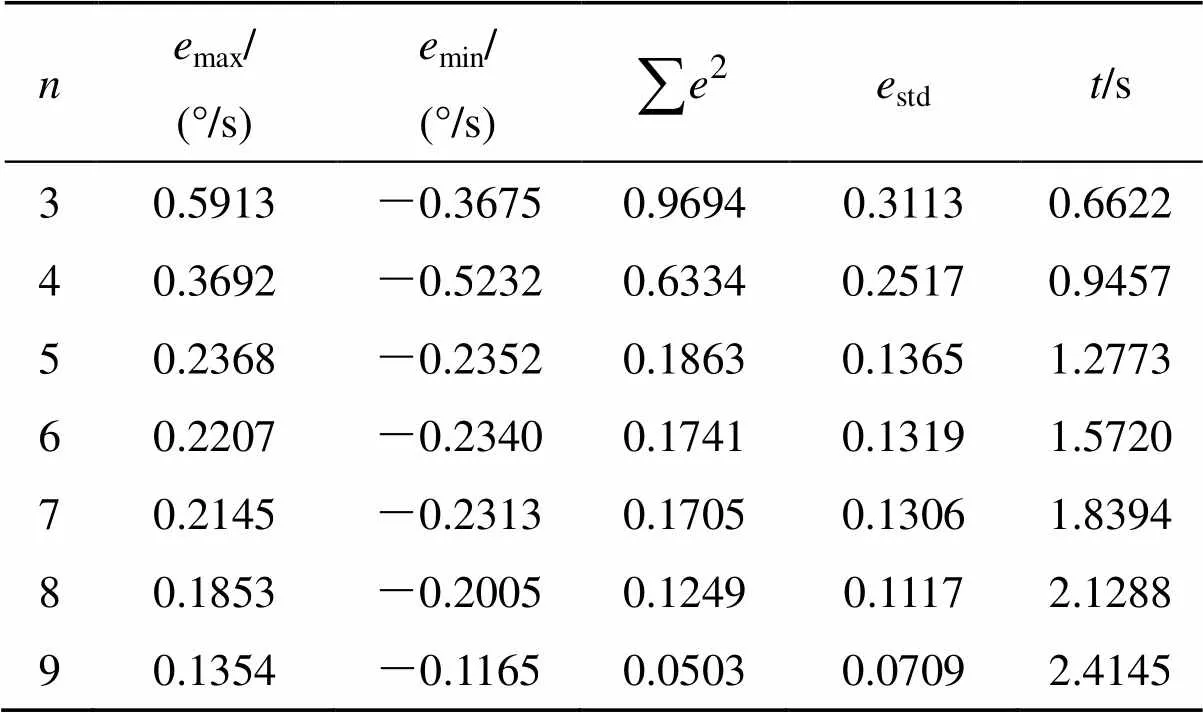
表1 n选取3~9时多项式拟合模型效果
=5时温度-零偏约束模型,如式(5)所示:
1(T)=-1.02675×10-13T5+1.46185×10-9×
T4-8.2987×10-6T3+0.0235T2-
33.0885T+21583.7263 (5)
式中:T表示陀螺的温度电压。
根据式(5)建立的温度-零偏约束模型,得到MEMS陀螺零位偏置速率与温度的拟合关系曲线如图2所示,并对陀螺输出速率信号的零偏进行补偿,效果如图3所示。
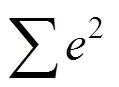
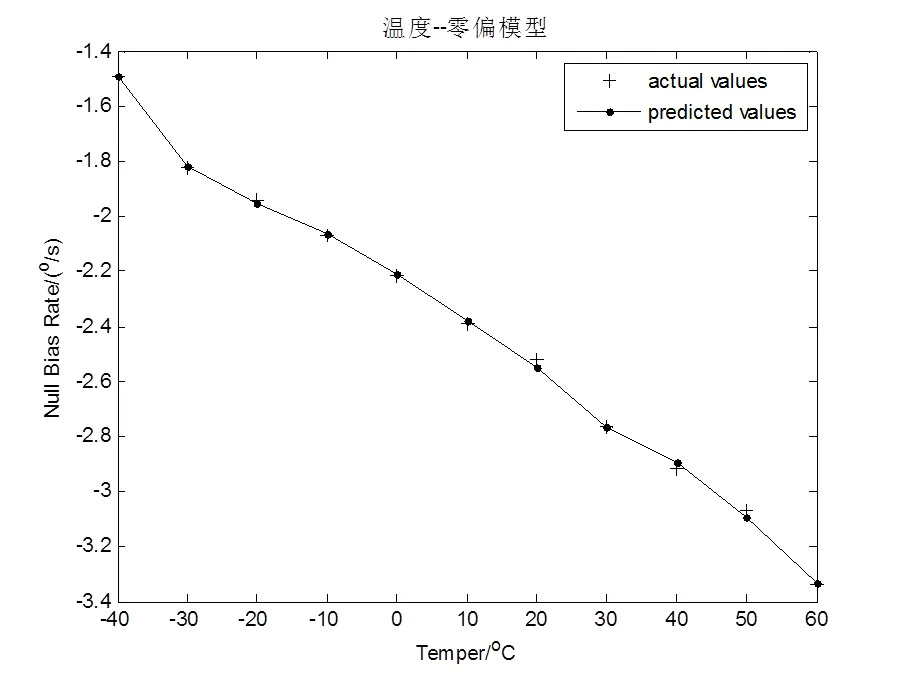
图2 温度-零偏约束模型曲线
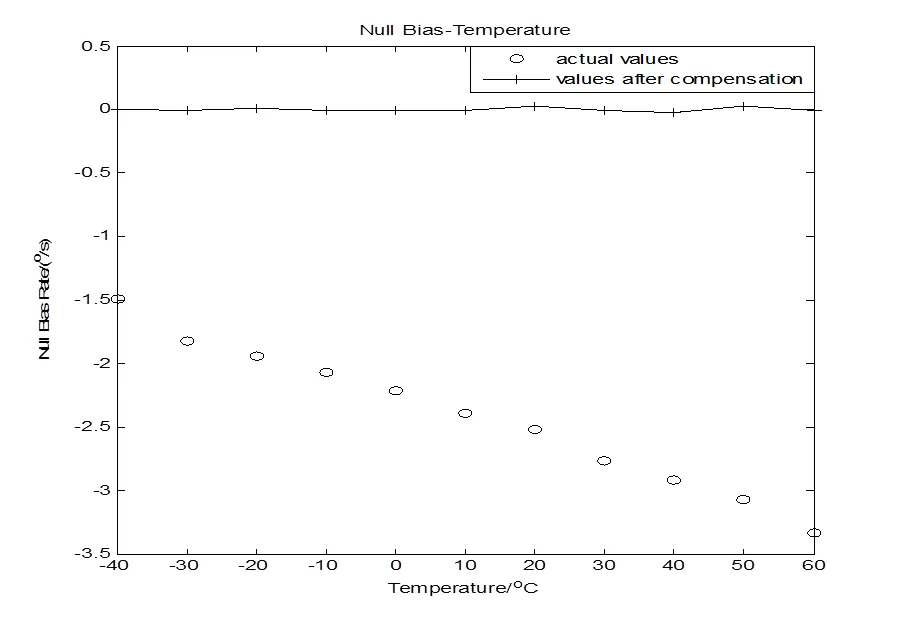
图3 补偿前后结果对比
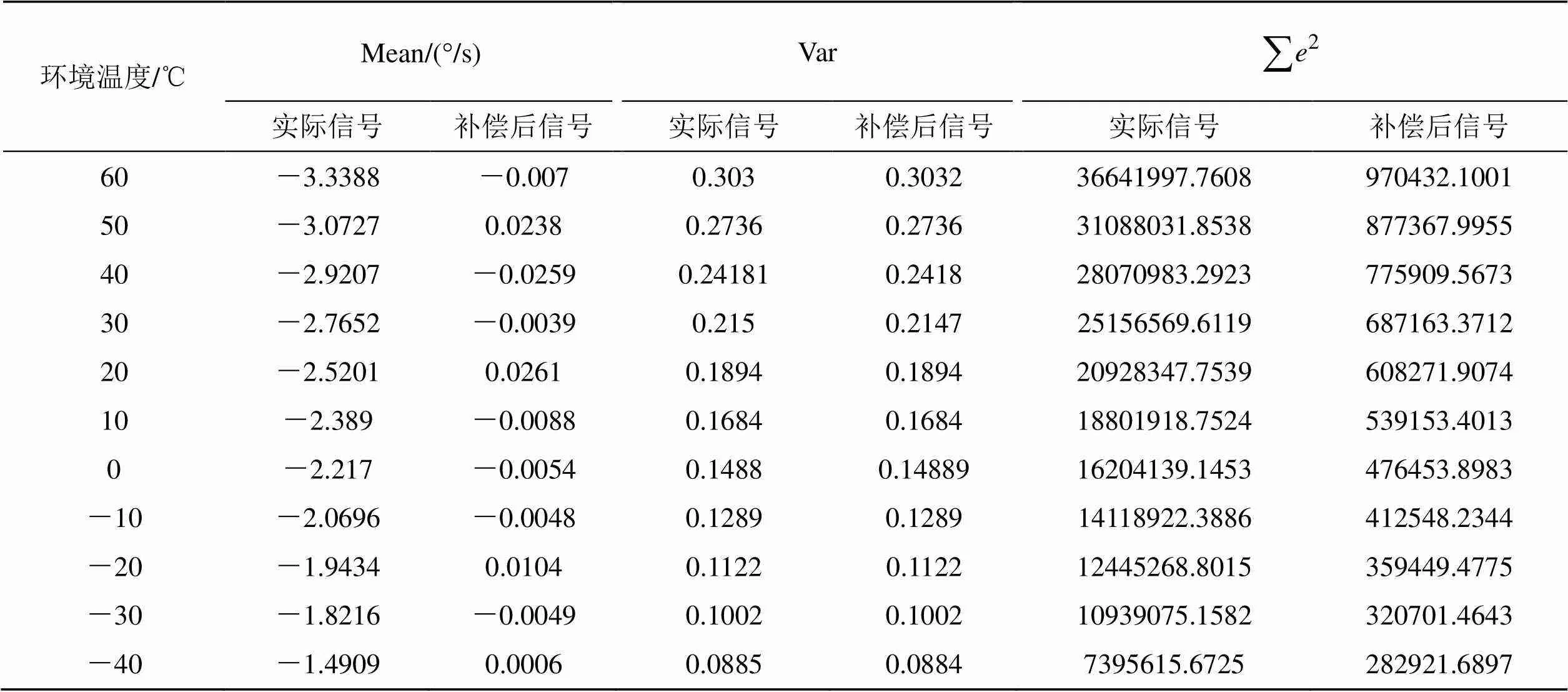
表2 60℃~-40℃下温度-零偏约束模型补偿效果
2.2 温度-主频率分量约束模型
对各环境温度点下采集的MEMS陀螺零位速率输出信号进行频谱分析,发现在有效温度范围内的任一温度点下,信号频谱在50Hz、96Hz、144Hz处幅值都略大,随温度的降低,幅值最大的主频率项会近似线性增大,如图4所示。
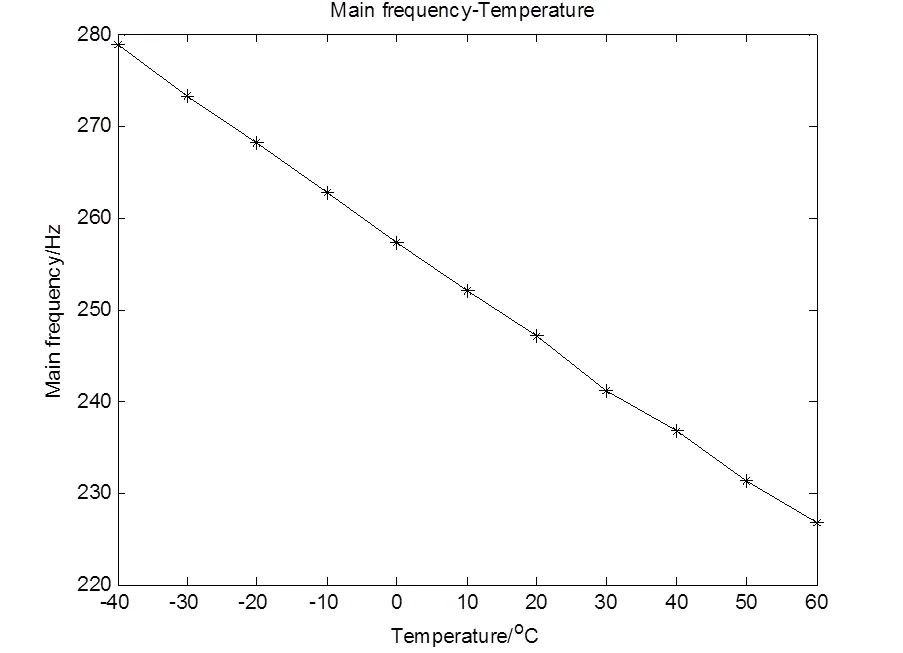
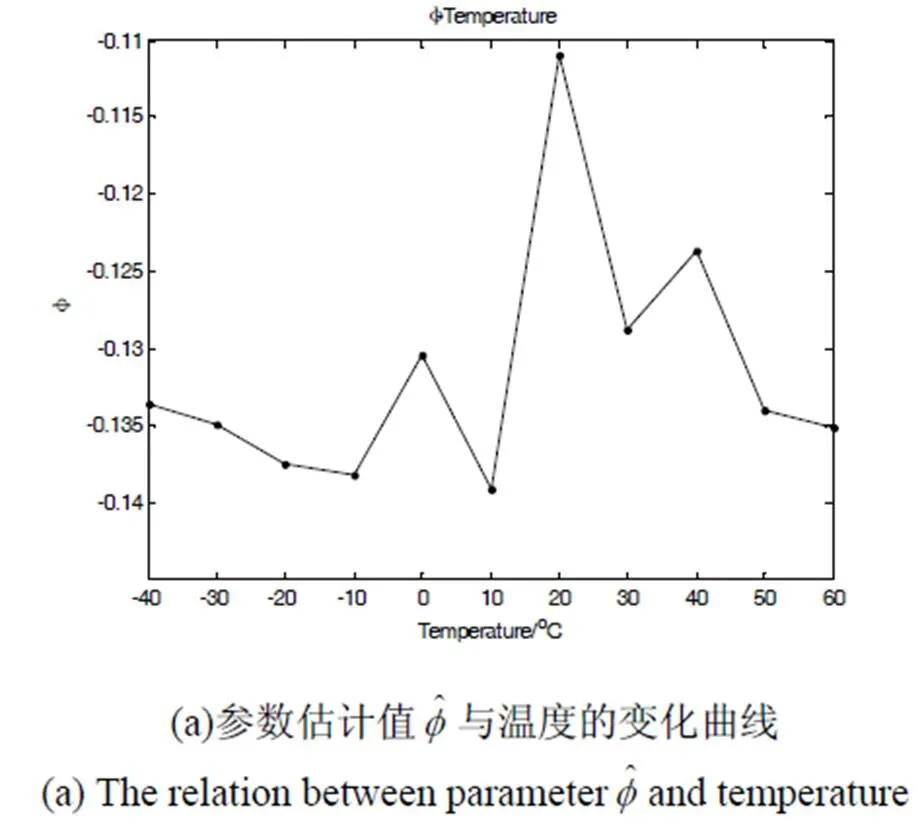
图4 主频率项与温度的关系曲线
由于主频率项与温度电压的关系曲线几乎与一阶线性模型吻合,利用一阶线性拟合估计模型参数:1=-0.0488,2=390.0549,具体模型如式(6)所示:
(T)=0.0488×T+390.0549 (6)
式中:(T)表示与温度电压相关、在频谱中幅值最大的主频率分量。
由图5知,信号主频率项与温度的模型同实际频率偏差值5Hz以下,该误差不会对主要周期项的辨识造成太大影响。依据本模型,可大致确定实验涵盖温度范围内的幅值最大的主要频率分量,将它同50Hz、96Hz、144Hz频率分量一起滤除,以达到去除周期项2()的目的。
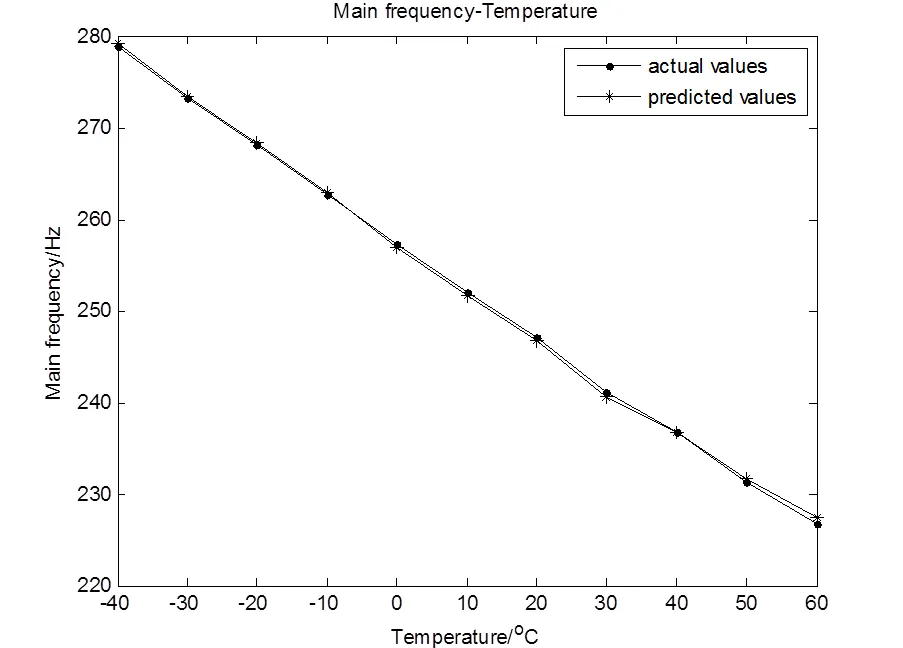
图5 主频率项与温度的模型 Fig.5 Temperature and main frequency relationship model
3 基于ARMA+Kalman零位随机漂移模型
在去除MEMS陀螺仪信号的异常值和去除其中的趋势项之后,必须对信号的平稳性和周期性作出判断,即对信号序列进行平稳性和周期性检验[10-11],以保证待建模序列的平稳性,避免ARMA模型的伪回归现象的出现。本文针对采集到的MEMS陀螺信号数据建立ARMA模型,加入Kalman经典滤波优化模型,完成MEMS陀螺零位随机误差项模型的建立和优化。
3.1 建模前信号序列的检验
对去除了温度引入确定性误差后的信号序列进行平稳性检验,验证信号中是否只有与温度相关的趋势项,以及信号中的趋势项是否已完全被去除。本文采用逆序法[10-11]检验信号序列的平稳性。具体方法为:将原始数据分段后求解各段均值,计算各段对应均值的逆序数之和;构造假设为信号序列无趋势;通过如式(7)的统计量值,判断是否接受假设;若值处于|2|之间,表明信号序列逆序法的检验结果与理论分析一致,信号序列中无趋势项,置信水平为0.05。
式中:为逆序数i之和,[]为i的期望,var[]为i的方差。
根据温度-零偏约束模型补偿温度引入的趋势项后,对信号进行逆序法检验,检验结果如表3所示。可见在不同温度下信号数据集的所有值处于|2|之间,表明与温度相关的趋势项被去除,补偿后的信号可以通过平稳性检验。

表3 逆序法检验结果
3.2 识别ARMA模型
MEMS陀螺的随机漂移较大是限制陀螺角速率精度的主要原因。将MEMS陀螺信号视为时间序列,从不同时刻间序列值相关性的角度来预测现时刻的序列值。因此借助ARMA模型能在一定程度上预测现时刻MEMS陀螺的漂移值。
ARMA(,)模型定义方程[9]为:
Y=1Y-1+2Y-2+…+Y-+e-
1×e-1-2×e-2-…- Y-(8)
根据采集到的MEMS陀螺零位速率样本数据发现,样本自相关函数和偏自相关函数[11]都属于拖尾性质,且在1阶较为显著,故选择ARMA(1,1)模型逼近MEMS陀螺零位随机漂移,模型如式(9)。通过检验残差序列的正态性和自相关性,判断残差为白噪声序列。因此,所选择的ARMA(1,1)模型合适:
Y=Y-1+e-e-1(9)
3.3 ARMA模型参数估计及校验
估计模型参数,可采用矩估计、最小二乘法、极大似然估计方法。文献[11]中通过列表展示了利用矩估计得到的参数估计值偏离真值的程度较大,最小二乘法、极大似然估计得到的参数估计值与真值较为接近。因此,本文选择最小二乘法估计参数值。
鉴于MEMS陀螺零位随机误差项受温度影响,会随温度升高而增大。因此,将受温度作用的零位随机误差转化为ARMA模型参数在各温度点下的变化。
对完成参数估计的ARMA模型,校验其有效性和正确性。若模型识别正确,且参数的估计值充分接近真实值,所得的残差就应该近似具有白噪声的性质[11],表现为具有独立同分布、零均值和相同标准差的正态变量。
根据图7所示的模型残差自相关序列图,残差的自相关函数(0)=1,()=0,表明残差序列具有独立性;由图8残差序列的正态分位数图(Sample Quantiles-Theoretical Quantiles,简称QQ图)看出,模型残差正态分位数图上的点呈现一条直线,表明模型的残差近似服从正态分布。且因为模型残差的平均值接近0,所以模型通过检验,未出现过度拟合和参数冗余。
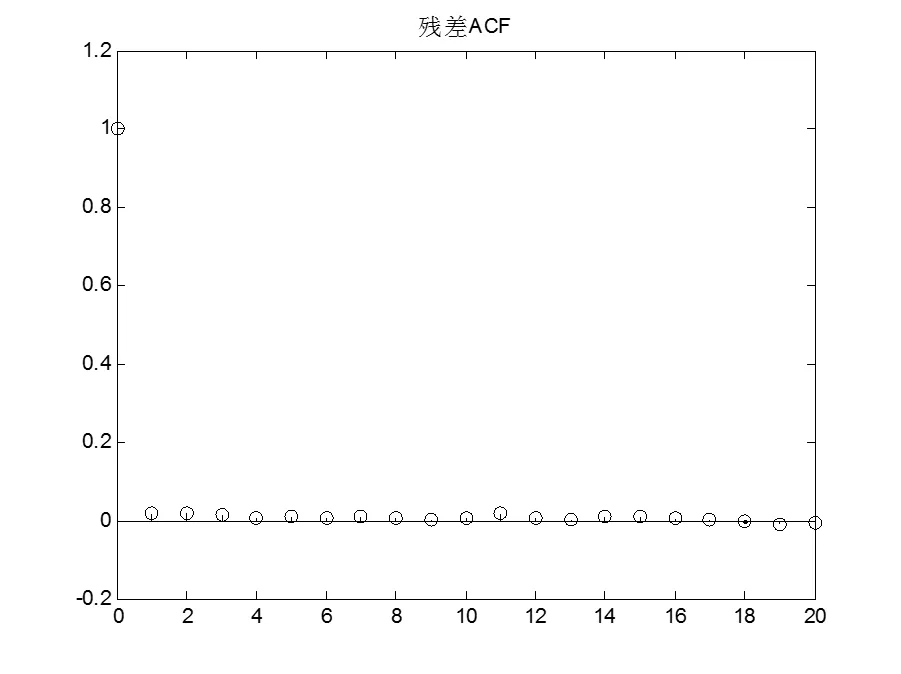
图7 残差序列的自相关序列
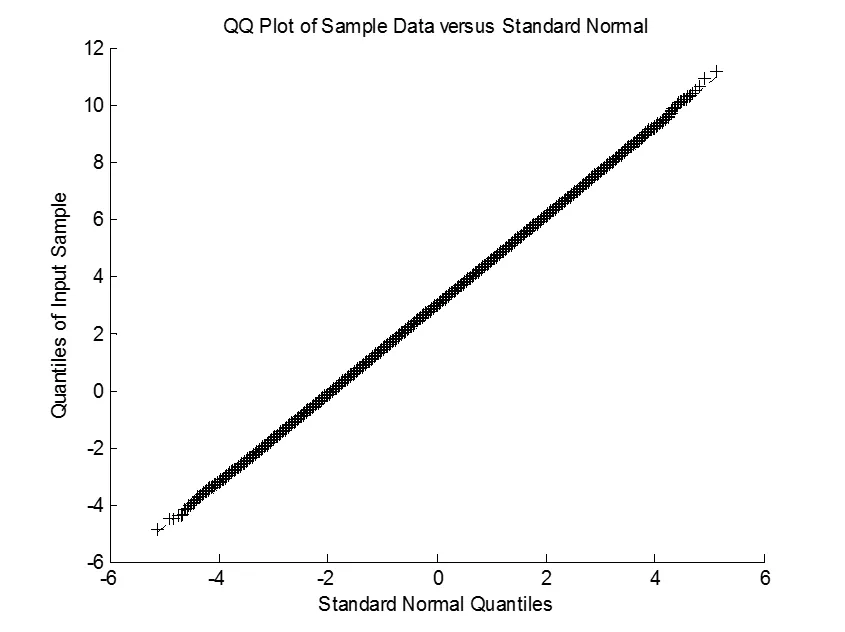
图8 残差序列的QQ图
3.4 基于Kalman滤波的ARMA模型优化
Kalman滤波[12-13]是目前应用较为广泛的实时最优线性滤波方法,但其本质上是一种以均方估计误差最小为原则的预测方法。通过Kalman滤波对ARMA模型进行优化,提高模型精度。
系统方程为:
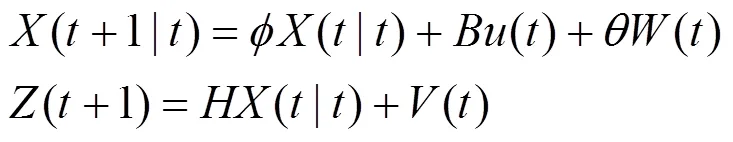
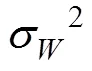
计算预测误差协方差矩阵为:
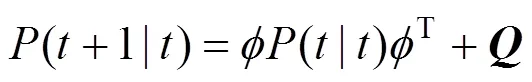
滤波增益矩阵:
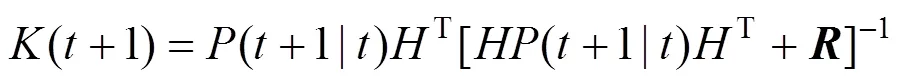
状态估计修正:
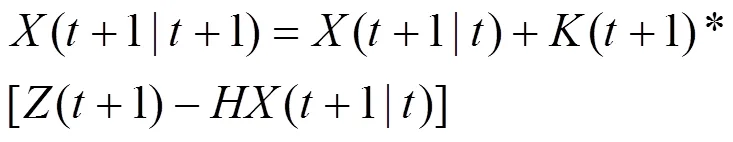
估计误差方阵:
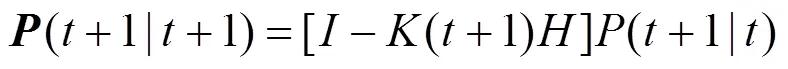
本文采用Kalman滤波方法,对建立的ARMA模型进行优化,有效削弱随机误差项,进一步提高模型精度。由图9可知,纵坐标都为等效的输入角速度,对原始信号进行ARMA模型建模补偿后信号的均值趋近于0°/s,标准差为0.8731;而加入Kalman滤波优化后,补偿后的信号标准差提升为0.0331。
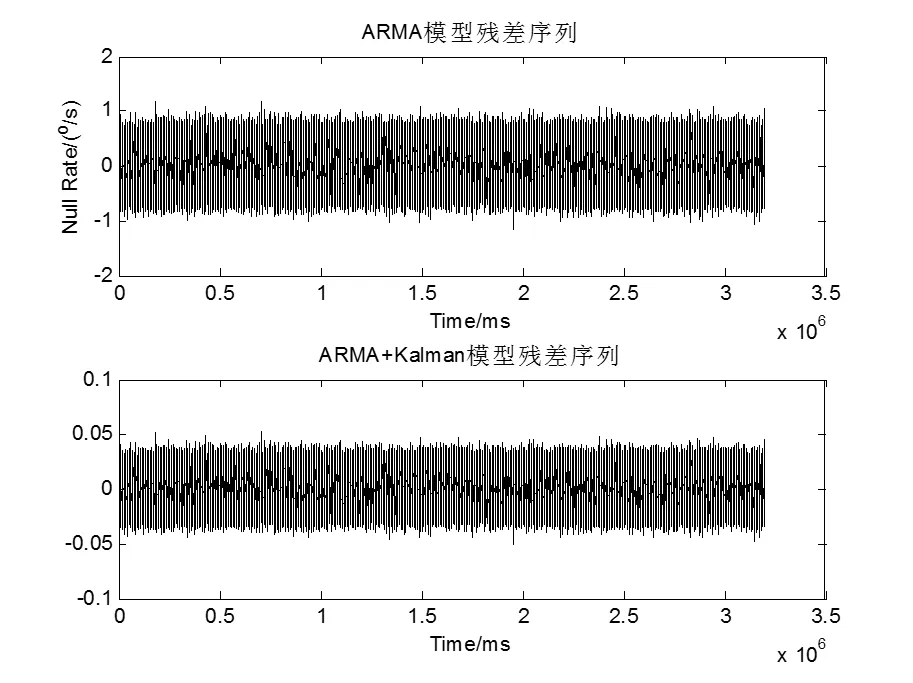
图9 加入Kalman滤波优化效果图
4 实验与仿真
采集某型MEMS陀螺在-40℃~60℃温度区间下间隔10℃采集的3组零位速率电压和温度电压输出取均值,采样率和采集时间与2.1节的实验相同,以此验证温度约束的MEMS陀螺零漂模型的有效性和补偿效果。实验流程如下:
1)根据温度-零偏约束模型,按照式(5)计算得到温度引入的确定性误差的预测值,消除温度趋势项。然后,采用逆序法,对加入温度-零偏约束模型补偿前后的信号序列进行平稳性检验。由表4可知,值基本处于|2|之间,除数据15号,值略大一点,近似看作-2,通过平稳性检验。
2)对信号序列频谱分析,采用温度-主频率分量约束模型选择的主频率分量的误差均值为10Hz,由于温箱重复性差的影响,将偏置去除后,误差均值为1Hz,并构建组合滤波器滤除信号序列中的周期项。
3)采用前面温度均值-参数估计值的建立的ARMA+Kalman模型,补偿MEMS陀螺零位漂移。温度约束补偿模型对MEMS陀螺零位漂移的补偿效果,见图10。
由图10可知,在-40℃~60℃下经过温度约束的零漂补偿模型补偿后,MEMS陀螺零位速率均值达到0.5º/h,方差的数量级在1.22×10-6左右,其他对比的技术指标见表5,表示模型误差,亦表示补偿后的信号。由此可证明该模型能有效补偿MEMS陀螺零位速率漂移。

表4 逆序法检验结果
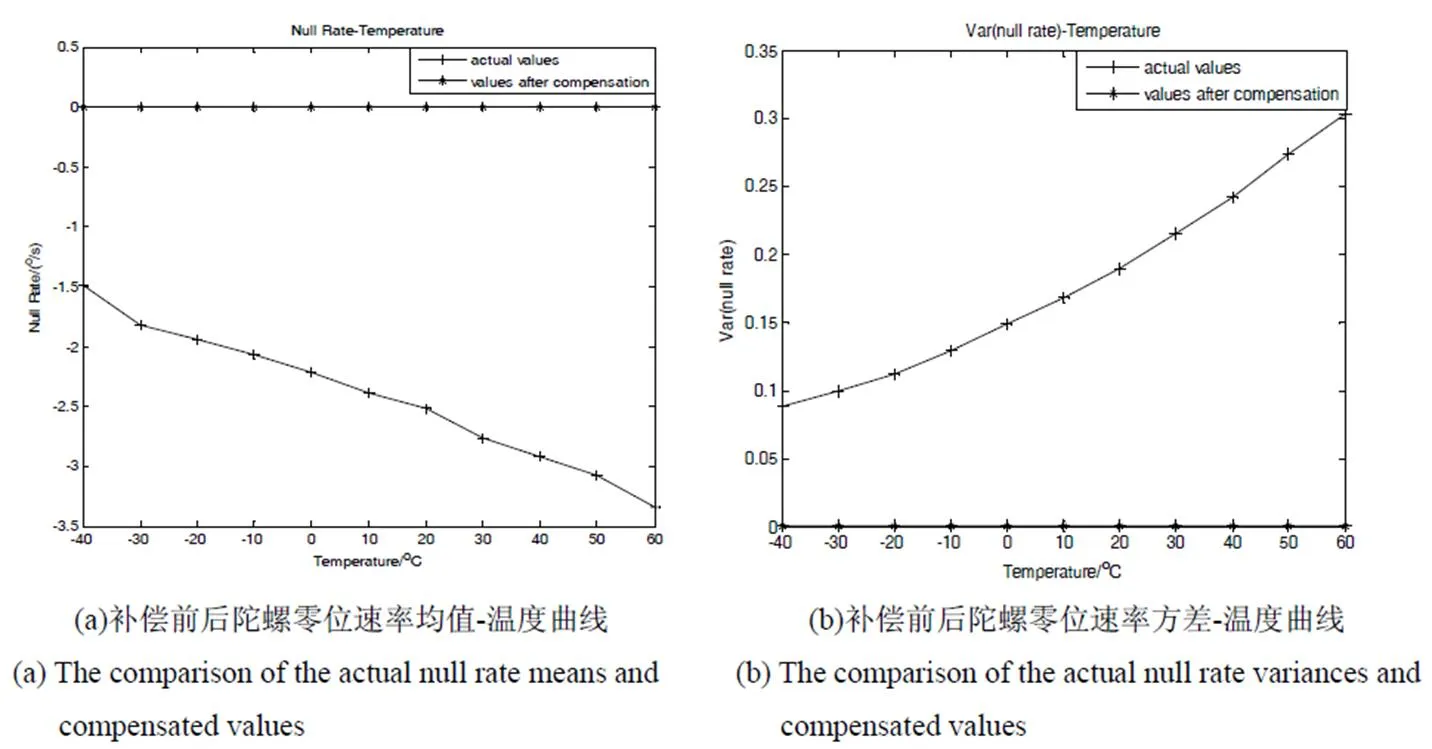
图10 在-40℃~60℃下补偿前后陀螺零位速率均值和方差曲线
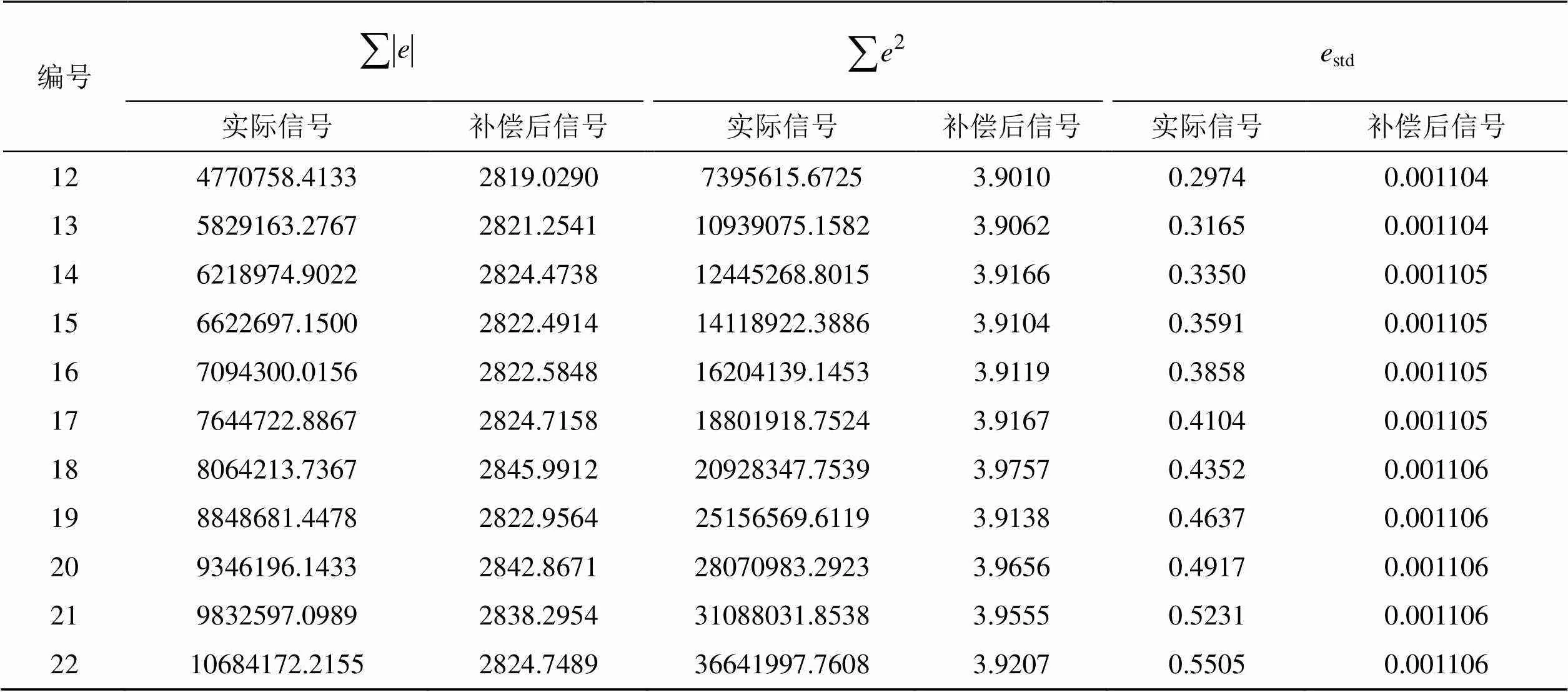
表5 温度约束的零漂补偿模型补偿后的信号与原信号的部分指标对比
5 结论
鉴于应用环境的需求,使得陀螺在选取时陷入性能与体积的矛盾抉择中。为满足陀螺尺寸与性能的双需求,必须采用可行方法提升MEMS陀螺的性能。根据MEMS陀螺的信号特征,本文提出一种温度约束的MEMS陀螺零漂补偿模型。该模型通过对温度引入的确定性误差项建立温度-零偏约束的模型和温度-主频率分量约束模型,利用ARMA模型对MEMS陀螺信号中的随机误差项建模,加入Kalman滤波优化预测效果,改善了MEMS陀螺信号零位漂移补偿模型精度。实验和仿真结果验证了本文提出的温度约束模型在陀螺零位漂移补偿的有效性。该方法为MEMS陀螺广泛可靠的应用奠定了技术基础。
[1] 程龙, 王寿荣, 叶甫. 硅微机械振动陀螺零偏温度补偿研究[J]. 传感技术学报, 2008, 21(3): 483-485.
CHENG Long, WANG Shourong, YE Pu. Research on bias temperature compensation for micromachined vibratory Gyroscope[J]., 2008, 21(3): 483-485.
[2] Igor P Prikhodko, Alexander A Trusov, Andrei M Shkel. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing[J].. 2013, 201: 517- 524.
[3] DU Jiaying, Christer Gerdtman, Maria Linden. Signal processing algorithms for temperature drift in a MEMS-gyro-based head mouse[C]//,, 2014: 12-15.
[4] 朱华征, 周晓尧, 张文博, 等. 光电稳定平台中陀螺随机漂移的处理方法[J]. 中国惯性技术学报, 2009, 17(2): 225-230.
ZHU Huazheng, ZHOU Xiaoyao, ZHANG Wenbo, et al. Processing of gyro drift for opto-electronic stabilization platform[J]., 2009, 17(2): 225-230.
[5] 王昊, 王俊璞, 田蔚风, 等. 梯度RBF神经网络在MEMS陀螺仪随机漂移建模中的应用[J]. 中国惯性技术学报, 2006, 14(4): 44-48.
WANG Hao, WANG Junpu, TIAN Weifeng, et al. Application of gradient radial basis function network in the modeling of MEMS gyro’s random drift [J]., 2006, 14(4): 44-48.
[6] 李士心, 王晓亮, 翁海娜, 等. 基于灰色模型和RBF神经网络的MEMS陀螺温度补偿[J]. 中国惯性技术学报, 2010, 18(6): 742-746.
LI Shixin, WANG Xiaoliang, WENG Haina, et al. Temperature compensation of MEMS gyroscope based on grey model and RBF neural network[J]., 2010, 18(6): 742-746.
[7] 陈湾湾, 陈志刚, 马林, 等. MEMS微机械陀螺温度特性分析与建模[J]. 传感技术学报, 2014, 27(2): 194-197.
CHEN Wanwan, CHEN Zhigang, MA Lin, et al. Analyzing and modeling of the thermal characteristics about MEMS Gyroscope[J]., 2014, 27(2): 194-197.
[8] 秦伟伟, 郑志强, 刘刚, 等. 基于小波分析与LSSVM的陀螺仪随机漂移建模[J]. 中国惯性技术学报, 2008, 16(6): 721-724.
QIN Weiwei, ZHENG Zhiqiang, LIU Gang, et al. Modeling method of gyroscope’s random drift based on wavelet analysis and LSSVM[J]., 2008, 16(6): 721-724.
[9] 谈振藩, 张勤拓. MEMS陀螺误差辨识与补偿[J]. 传感器与微系统, 2010, 29(3): 39-41.
TAN Zhenfan, ZHANG Qintuo. Error identification and compensation of MEMS gyroscope[J]., 2010, 29(3): 39-41.
[10] 何昆鹏. MEMS惯性器件参数辨识及系统误差补偿技术[D]. 哈尔滨: 哈尔滨工程大学, 2009.
HE Kunpeng. Parametric Identification and Error Compensation of MEMS Inertial Sensors and IMU[D]. Ha’erbin: Harbin Engineering University, 2009.
[11] Jonathan D Cryer, Kung-Sik Chan. 时间序列分析及应用[M]. 北京: 机械工业出版社, 2011.
Jonathan D Cryer, Kung-Sik Chan.[M]. Beijing: China Machine Press, 2011.
[12] 吉训生, 王寿荣, 许宜申, 等. 自适应Kalman滤波在MEMS陀螺仪信号处理中的应用[J]. 传感器与微系统, 2006, 25(9): 79-81.
JI Xunsheng, WANG Shourong, XU Yishen, et al. Application of the adaptive Kalman filter in the MEMS gyro signal processing[J]., 2006, 25(9): 79-81.
[13] 陈晨, 赵文宏, 徐慧鑫, 等. 基于卡尔曼滤波的MEMS陀螺仪漂移补偿[J]. 机电工程, 2013, 30(3): 311-313.
CHEN Chen, ZHAO Wenhong, XU Huixin, et al. Compensation of MEMS gyroscope error based on Kalman filter[J]., 2013, 30(3): 311-313.
Compensation Model of MEMS Gyroscope’s Null Shift Based on Temperature Constraint Algorithm
YAN Xinjie,LIN Yu,LI Jian,ZHANG Jin,LIN Dandan
(Kunming Institute of Physics, Kunming 650223, China)
To avoid the shortcomings of the compensation of null output of MEMS gyroscopes, this paper presents a null shift compensation model for MEMS gyroscopes based on temperature constraint model. Firstly, according to the measurement model of MEMS gyros’ signal, which consists of the definite error and the stochastic one. The temperature-null bias voltage constraint model and temperature-main frequency constraint model are proposed on the definite error effected by temperature. And the models can weaken the definite and season parts effectively. Then, the ARMA model is used to predict the rest stochastic error of MEMS gyros’ signal. At last, Kalman filter is made by optimizing the established ARMA model, which aims at the improvement of the model’s performance. The theoretical analysis and experimental results show the robust and efficiency of the model proposed.
temperature constraint,null shift compensation,MEMS gyroscope
TP273
A
1001-8891(2017)01-0073-08
2016-08-10;
2016-08-31.
阎歆婕(1991-),女,硕士研究生,云南昆明人,主要研究方向为伺服控制中的信号处理。
林宇(1972-),男,研究员级高级工程师,硕士生导师,云南昆明人,主要从事光电系统的研究。

