红外热波技术在热障涂层厚度检测上的应用研究

李永君，肖俊峰，朱立春，张 炯，高斯峰，唐文书，南 晴



红外热波技术在热障涂层厚度检测上的应用研究

李永君，肖俊峰，朱立春，张 炯，高斯峰，唐文书，南 晴

（西安热工研究院有限公司，陕西 西安 710054）

为快速准确地测量热障涂层厚度，采用基于热图序列特征时间的闪光灯激励红外热波测量方法，通过建立半无限大和有限厚度两种平板传热模型，提出根据热障涂层表面温度对数曲线线性回归时间选择二阶微分曲线负峰值时间的方法，解决了采用普通帧频热像仪采集的涂层表面温度曲线二阶微分负峰较多，无法确定特征峰值时间的困难，热障涂层厚度测量相对误差小于10%，满足工程应用要求。

热障涂层；红外热波；热图序列；厚度测量

0 引言

热障涂层是目前最为先进的高温防护涂层之一，具有良好的隔热效果和抗氧化性能，被广泛应用于燃气轮机热通道部件（如透平叶片，燃烧室等）表面防护中。其中涂层厚度是表征热障涂层质量的关键技术指标，它关系到涂层的使用寿命、结合强度、不均匀内应力和制造成本等的评估和计算[1-2]。

目前，热障涂层厚度测量方法包括有损和无损检测2种，有损检测具有破坏性且测量数据较片面[3]。无损检测主要有涡流法、超声波法和红外法等。涡流法机理为提离效应，受粘结层特性影响较大[4-5]；超声波法需提取超声回波频域信号中2相邻谐振频率差来计算涂层厚度，谐振频率干扰因素较多，测量准确度难以保证，且步骤复杂[6]，上述2种方法均不适合非接触快速检测。

红外热波技术具有非接触、快速、观测面积大、准确率高等优势，非常适合外场在线检测。目前国内外学者采用红外热波技术进行涂层测厚一般均基于涂层表面温度序列的对数二阶微分曲线峰值时间（即热图序列特征时间）进行推导。如Shepard S M[7]等人利用高帧（180Hz）热像仪，基于热图序列特征时间，对热障涂层厚度进行测量，但高帧热像仪成本极高，工业应用较少。陶胜杰[8]等人采用普通帧频（50Hz）热像仪，对丙烯酸黑色漆涂层进行厚度检测，误差≤7%。但由于热障涂层为非严格各向同性均质体，具有半透明性，且表面粗糙度较高，当采用普通帧频热像仪进行检测时，存在热图温度二阶微分曲线负峰较多，特征时间难以选取的困难。

因此，本文利用普通帧频（60Hz）热像仪结合闪光灯激励红外热波技术，基于热图序列特征时间，通过理论模型分析和实验验证相结合的方法，对高温合金基体上热障涂层厚度进行测量研究，探索其可行性，以期其检测误差满足工业应用要求。

1 实验设备及试样设计

本实验采用美国TWI公司的Echo Therm红外热波检测系统，主要包括热像仪、热激励系统、计算机及专用控制软件、图像采集和处理系统。热像仪为FLIR公司的Therma-CAMSC3000焦平面制冷型热像仪，图像大小为320×240像素，响应波段为8～9mm，采集帧频为60Hz，采集时间为15s，热灵敏度为20mK；热激励系统为两个4.8kJ的闪光灯，光脉冲宽度为2ms；使用日本电子株式会社的JSM-6360型扫描电镜观察涂层厚度；涂层试样为双层热障涂层结构，里层粘结层成分为Ni-22Cr-9Al-37Co-0.5Y，表层陶瓷层成分为7～8wt%Y2O3稳定ZrO2，基体合金为K438镍基高温合金，厚度为15mm。在涂层表面喷涂一层水溶性黑漆，以增加表面对可见光的吸收以及表面的红外辐射，结构示意图如图1所示。试样1、试样2、试样3和试样4粘结层设计厚度相同，均为150mm。陶瓷层设计厚度相差较大，试样1到试样4陶瓷层厚度依次增加，分别为100、150、200和400mm，粘结层和陶瓷层均采用大气等离子喷涂工艺制备。

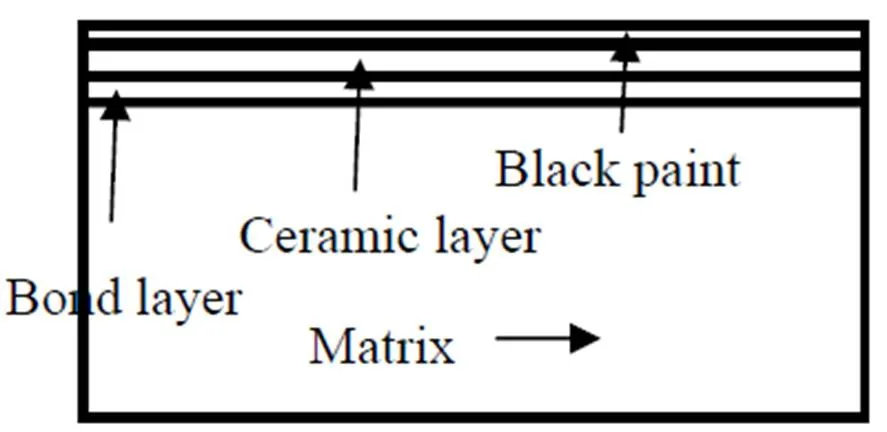
图1 涂层结构示意图

2 红外热波检测涂层厚度原理

2.1 半无限大平板传热分析

对半无限大平板材料，如图2[9-10]所示，代表单位面积的总热量，热源瞬时作用在平板表面上，由于是平板表面，只考虑热量在厚度方向上的一维传导，热传导方程的一维形式为：

公式(1)的解为：

将公式(2)两边取自然对数，得到：

式中：Q为热量；a为热扩散系数；C为比热容；k为热扩散系数；T为温度；t为时间。根据公式(3)可知，在对数坐标里，半无限大平板受脉冲激励后表面温度随时间呈斜率为－0.5的线性变化[9]。

2.2 有限厚度平板传热分析

对厚度为的均质平板材料，如图2(b)所示，对其表面施加一瞬时脉冲热源，脉冲能量在试件表面较小深度范围内被吸收，时刻温度分布可写为：

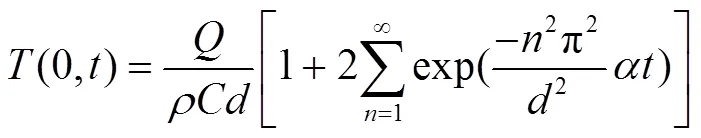
令＝p2t/2，在对数坐标下对公式(5)求解二阶导数，得到：

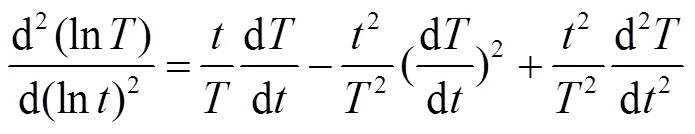
对公式(5)求解一阶导数和二阶导数，得到：

将公式(7)和(8)代入公式(6)中，求解公式(6)对应的峰值时间为：

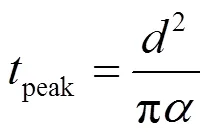
从公式(9)可以看出，当被测平板厚度一定时，厚度的平方与其表面对数温度的二阶微分峰值时间成正比，比例系数由平板材料的热扩散系数确定[10]。对于本实验中热障涂层试样，由于粘结层设计厚度相近，且粘结层成分与基体合金相近，二者导热特性相差不大[11]，故假设粘结层和基体为一整体，只分析不同厚度陶瓷层的传热特性。对于一定厚度的陶瓷涂层，传热特性类似有限厚度的平板模型，只要在特定已知涂层厚度的试样上测量不同的二阶微分峰值时间peak，拟合换算得到值。然后通过测量未知涂层厚度的试样peak值，就可以根据公式(9)求得涂层厚度值。

3 实验检测结果及分析

3.1 涂层厚度红外热波检测结果

1）热图检测结果

涂层试样的检测热图如图3所示。结果表明，在第1帧，＝0.017s时，4块试样灰度呈现明显差别，以灰度表示的热图中，通常亮度越高温度越高，即4块试样呈现的温度场不一样，这是由于涂层的厚度不同导致涂层受热激励后热量传导不一致，反射到表面的热波强度不同。在第100帧，＝1.668s时，4块样基本没有明显的灰度差别，即热量从涂层传到基底后达到热平衡状态，表面温度大体无差异。

图3 涂层试样检测热图结果

2）热图序列特征时间提取

为了减小热像仪的温度噪声，提高数据精度，选择大小为3×3像素的一块小区域，把相应小区域内所有点的温度取均值后进行归一化，做出不同厚度热障涂层表面的温度曲线，如图4所示。结果表明，初始时脉冲激励作用使4块涂层表面都获得了较高的温度，表面温度会在一个非常短时间内快速下降，最后，降至室温，4条曲线逐渐重合在一起。

图5和图6分别为温度-时间对数曲线和其二阶微分曲线。结果表明，二阶微分曲线的峰值时间较多，且同时出现多个正峰和负峰，难以判别peak具体时间。分析主要有3个原因：一是本实验热像仪的采集频率最高为60Hz，所以温度采集不可避免出现时间间隙，导致曲线出现波动，峰值较多，无法完全符合理论值；二是理论曲线是建立在一维的热传导模型基础上，由于热障涂层并不是严格的各向同性均质体，结构中存在大量微孔洞、夹杂物等，因此，不可避免地受三维热扩散的影响，导致曲线出现波动；三是红外检测时会受到环境温度、气流干扰影响，温度曲线会出现波动现象。所以，需要结合温度-时间对数曲线来综合判断peak具体时间。

图4 涂层试样表面温度-时间曲线

图5 涂层试样表面温度-时间对数曲线

图6 涂层试样表面温度-时间二阶微分曲线

由图6知，试样1温度-时间二阶微分曲线没有明显的负峰值出现，这是由于试样1涂层厚度较小，传热加速的负峰值时间较短，本实验热像仪采集帧频为60Hz，难以采集到该试样的细微温度变化信息。据Shepard S M等[7]的研究推荐，当热障涂层陶瓷层厚度小于45mm时，需采用帧频大于180Hz的热像仪。

试样1涂层厚度较小，近似基体合金传热现象，符合半无限大平板传热模型，温度-时间对数曲线按斜率近似为－0.5线性变化，如公式(3)和图5所示。当基体合金表面有涂层材料时，热量传导符合有限厚度平板传热模型，热波在涂层界面发生反射，对应表面温度-时间对数曲线偏离线性变化，厚度越大，表面温度越高，线性偏离越大。当传热到涂层/基体界面处时，转变为半无限大平板传热模型，表面温度-时间对数曲线趋于线性，该线性回归时间也正是对数二阶微分曲线的加速传热峰值时间。因此，对于存在多个负峰值时间的二阶微分曲线，需选取的负峰值时间（图6中3条竖直虚线）应与对数曲线的线性回归时间（图5中3条竖直虚线）相接近，各试样的负峰值时间选取结果如表1所示。

3.2 涂层厚度扫描电镜检测结果

对不同厚度涂层试样的3×3像素区域纵向切割后制备扫描电镜试样进行厚度测量，如图7所示。结果表明，试样涂层厚度较均匀，粘结层/基体以及陶瓷层/粘结层界面结合良好。对区域内按顺序等距离选取的5个位置进行陶瓷层和粘结层厚度测量，结果如表2所示，4个试样陶瓷层厚度相差较大，粘结层厚度接近，与实验设计相符。

3.3 厚度检测结果对比

令公式(9)中的1/(p)＝，则写为：

peak＝2(10)

据Zhao等[13]的研究推荐，值一般取7.793×10－6，将表2中的峰值时间代入公式(10)，得出不同试样陶瓷层厚度值，如表3所示。结果表明，采用闪光灯激励红外热波法测量的热障涂层陶瓷层厚度与实际厚度相比，相对误差均小于10%，满足工程应用要求。

4 结论

采用普通帧频（60Hz）热像仪结合闪光灯激励红外热波技术，对高温合金基体上热障涂层陶瓷层厚度进行测量。基于热图序列特征时间，根据热障涂层表面温度对数曲线线性回归时间选择二阶微分曲线负峰值特征时间，测量结果与实际厚度对比，相对误差小于10%，满足工程应用需求。可见利用闪光灯激励红外热波法检测热障涂层厚度技术可行，具有非接触、观测面积大、设备轻巧便携、测量数据准确可靠等优点，适合现场在役检测，具有巨大的应用价值和推广前景。

表1 温度-时间对数二阶微分曲线负峰值时间

图7 涂层扫描电子显微镜图

表2 涂层厚度扫描电镜测量值

表3 陶瓷层测量厚度对比

[1] Lu Z, Myoung S W, Kim E H, et al. Microstructure Evolution and Thermal Durability with Coating Thickness in APS Thermal Barrier Coatings[J]., 2014, 1(1): 35-43.

[2] Fang Xufei, Zhang Guobing, Feng Xue. Performance of TBCs system due to the different thickness of top ceramic layer[J]., 2015, 41(2): 2840-2846.

[3] Moskal G, Witala B, Rozmyslowska A. Metallographic preparation of the conventional and new TBC layers[J]., 2009, 39(1): 53-60.

[4] Li Yong, Chen Zhenmao, Mao Ying, et al. Quantitative evaluation of thermal barrier coating based on eddy current technique[J]., 2012, 50(1): 29-35.

[5] 倪立勇, 杨震晓, 马康智, 等. 等离子喷涂热障涂层厚度测量方法研究[J]. 热喷涂技术, 2015, 7(4): 22-30.

NI Liyong, YANG Zhenxiao, Ma Kangzhi, et al. Study on thickness of thermal barrier coating deposited by plasma spraying[J]., 2015, 7(4): 22-30.

[6] Ma Zhiyuan, Zhao Yang, Luo Zhongbing, et al. Ultrasonic characterization of thermally grown oxide in thermal barrier coating by reflection coefficient amplitude spectrum[J]., 2014, 54(4): 1005-1009.

[7] Shepard S M, Hou Y, Lhota J R, et al. Thermographic measurement of thermal barrier coating thickness[C]//.XXⅦ,, 2005, 5782(1): 407-410.

[8] 陶胜杰, 杨正伟, 张炜, 等. 基于热图序列时间特征的涂层厚度测量研究[J]. 仪器仪表学报, 2014, 35(8): 1810-1816.

TAO Shengjie, YANG Zhengwei, ZHANG Wei, et al. Research on measurement of coating thickness based on thermal image time characteristic[J]., 2014, 35(8): 1810-1816.

[9] 霍雁, 张存林. 碳纤维复合材料内部缺陷深度的定量红外检测[J]. 物理学报, 2012, 61(14): 1-7.

HUO Yan, ZHANG Chunlin. Quantitative infrared prediction method for defect depth in carbon fiber reinforced plastics composite[J].., 2012, 61(14): 1-7.

[10] 王中华, 曾智, 张存林, 等. 基于对数二阶微分峰值法的缺陷深度测量研究[J]. 红外, 2013, 34(3): 21-31.

WANG Zhonghua, ZENG Zhi, ZHANG Chunlin, et al. Study of defect-depth measurement based on second-order derivative peak value method[J]., 2013, 34(3): 21-31.

[11] Ptaszek G, Cawley P, Almond D, et al. Artificial disbonds for calibration of transient thermography inspection of thermal barrier coating systems[C]//, 2012: 491-498.

[12] Shepard S M, Lhota J R, Rubadeux B A, et al. Reconstruction and enhancement of active thermographic image sequences[J]., 2003, 42(5): 1337-1342.

[13] Zhao Shibin, Wang Huaming, Wu Naiming, et al. Nondestructive testing of the fatigue properties of air plasma sprayed thermal barrier coatings by pulsed thermography[J]., 2015, 51(7): 445-456.

Applications of the Infrared Thermal Wave Technology in Thermal Barrier Coating Thickness Testing

LI Yongjun，XIAO Junfeng，ZHU Lichun，ZHANG Jiong，GAO Sifeng，TANG Wenshu，NAN Qing

(,,710054,)

In order to measure the thermal barrier coating thickness efficiently and accurately, infrared flash thermography technology based on thermal image characteristic time was adopted. A method to choose the negative peak time of the second-order differential curve according to the linear regression time of the thermal barrier coating surface temperature log curve was proposed by establishing a half-infinite and finite-thickness plate heat transfer model. The problem of inability to determine the negative peak time because of multiple negative peaks of second-order differential curve using common-frame-frequency thermal imager was solved. The relative measurement error of coating thickness was less than 10% and it meets the requirements of engineering applications.

thermal barrier coating，infrared thermal wave，thermal image，thickness measurement

TN219

A

1001-8891(2017)07-0669-06

2016-10-28；

2017-06-22.

李永君（1987-），男，硕士，工程师，主要从事红外检测技术方面的研究。E-mail：lee19870914 @163.com。

肖俊峰（1974-），男，研究员，主要从事汽轮机及燃气轮机相关技术研究。E-mail：xiaojunfeng@tpri.com.cn。

华能集团总部科技项目（HNKJ15-H05）；国家自然科学基金（51501151）。