应用于红外制导武器的动力随动陀螺误差分析

雷 昊，杨海容，朱 牧，钮赛赛，杨 尧

（1.上海航天控制研究所，上海201109；2.西北工业大学航天学院，陕西西安710072）

应用于红外制导武器的动力随动陀螺误差分析

雷 昊1，杨海容1，朱 牧1，钮赛赛1，杨 尧2

（1.上海航天控制研究所，上海201109；2.西北工业大学航天学院，陕西西安710072）

为减小红外制导武器导引头的动力随动陀螺误差，对陀螺的误差进行了分析。用拉格朗日方法建立了动力陀螺完备的运动微分方程。将陀螺误差分为结构非理想化导致的漂移误差和稳速力矩与进动力矩耦合引起的控制误差两大类。其中：结构非理想的误差包括章动、摩擦力矩和非等弹性力引起的误差。用逐次逼近求解法分析，发现陀螺受阶跃力矩或冲击后，除按章动频率及高次谐波频率高频振动外，还会发生角速度为常值的漂移，且动力随动陀螺漂移的角速度与初始的角速度和内外环质量有关。讨论了由偏角、不平衡力矩和非等弹性力造成误差的机理。给出了陀螺主要误差的控制和调控方法：对漂移误差，尽量减小内外环质量，减小陀螺阶跃力矩后的初速；对工艺误差，调试时先部件后总体，总体调试由内及外；先大误差项，再小误差项；用力矩补偿法消除力矩耦合偏差。研究为导引头的误差分析和控制系统设计提供参考。

红外导引头；动力随动陀螺；拉格朗日方程；动力学模型；旋转磁场；方位角效应；误差补偿；漂移误差；控制误差

0 引言

现代多种战术武器系统广泛采用了红外导引系统［1］。在红外导引系统动力随动陀螺的设计调试中，陀螺的转轴与视线总存在一定的偏差，且陀螺的进动力矩在大偏角时会存在衰减而无法控制陀螺进动，这些现象都是由陀螺误差引起的，因此需要对动力随动陀螺误差进行研究，以寻求解决方案。对大部分种类陀螺的误差建模，通常将陀螺简化为带阻尼的二阶微分元件，这种简化后的方程在某些工程领域被称为陀螺技术方程。虽然陀螺技术方程便于设计，但简化处理会忽略多个造成误差的因素。传统的误差研究方法主要分两类。一类是建立陀螺的漂移误差模型，用系统辨识方法测定漂移系数［2］。但此法实现较复杂，不具在同类陀螺中使用的移植性，且陀螺在不同应用环境中误差模型差异很大。另一类是利用新兴工程方法分析误差，文献［3］利用键合图方法分析了动力调谐陀螺误差，但该法依靠新兴理论，误差的来源因素和物理意义不明显，工艺上很难提出可行的消除误差的统一标准和措施。针对红外导引头动力随动陀螺的特殊结构，本文考虑陀螺在大偏角工作状态下，先用拉格朗日第二方程建立完备的陀螺运动微分方程，并基于此完备的运动微分方程，分析了影响陀螺精度的因素，并提出了对随动陀螺主要误差的调控方法。

1 位标器陀螺的完备动力学模型

根据动力随动陀螺导引头的结构，基于文献［4］提供拉格朗日方程的方法，考虑万向支架内外环的质量和各干扰力造成的干扰力矩，建立动力随动陀螺转子模型为

式中：α，β，φ为三自由度陀螺广义坐标系中的三个独立转角；Jcx，Jcy，Jcz，Jbx，Jby，Jbz，Jax，Jay，Jaz分别为进动陀螺转子、内环总体和外环总体相对内环坐标系的转动惯量；Mx，My，Mz为忽略偏角耦合的进动控制力矩；为内环坐标系各向的随时间和位置变化的干扰力矩总和。

动力随动陀螺的转子轴为oz轴，在oz轴用基准线圈提供力矩补偿阻力矩，故理想状态下可认为Mz＝0，则为常值。此处：H为陀螺转子的动量矩。位标器动力随动陀螺的转子是高速旋转，通常自转角速度是每分钟数千甚至数万转以上，而进动角速度则相对较小，涉及进动角速度的量多为小量可忽略不计。由此，式（1）可简化为

式（2）即为导引头动力随动陀螺的运动微分方程。

2 导引头位标器误差

当陀螺被应用为惯性导航中的测量元件时，评价陀螺元件性能的最重要指标是陀螺漂移速度的大小。陀螺漂移指的是在外力矩等于零时，陀螺在微小的干扰力矩作用下，出现H缓慢偏离原方向的现象，陀螺漂移是陀螺误差最直接的反映。对导引头来说，动力随动陀螺不仅是测量元件而且是一种执行元件，在陀螺进动力矩和基准力矩的作用下，陀螺的纵向轴需时刻指向目标。因此，红外导引头动力随动陀螺的误差主要源于陀螺结构非理想化导致的漂移误差和力矩耦合引起的控制误差。

2.1 陀螺结构非理想化导致的漂移误差

2.1.1 章动引起的误差

在分析和设计初期，对动力随动陀螺的模型只需参考陀螺技术方程，但在分析误差并提高精度时，陀螺技术方程的推导过程所作的较多非线性小量线性化处理会导致实际结果与计算值存在一定的偏差。对理想动力随动陀螺，可视作陀螺的重心与框架中心完全重合，且在内外环上无干扰力矩。由陀螺的简化技术方程，分析易得在冲击力作用后陀螺的运动规律为高频振幅的章动［5］，章动可被快速阻尼，将陀螺的轴视为方向不变的定轴，但此结论并不完善。本文由完备的陀螺微分方程，分析理想动力随动陀螺在脉冲力矩干扰后的运动。

设陀螺初始状态非零Jy＝Jcy＋Jby，Jx＝Jcx＋Jbx，A＝Jcy＋Jby－Jbz＝Jy－Jbz，内外环上的干扰力矩为零，陀螺的初始位置为［α（0） β（0）］＝［α0β0］，设代入完备的陀螺运动学方程式（1）［6］。则

展开式（3），设Jy1＝Jbzsin2β0＋Jycos2β0＋Jay，略去α，β二阶以上的高阶微量项，整理到非线性非齐次方程

式（4）为非线性方程，用逐次逼近解法，忽略非线性部分构造齐次方程，得

为简化计算，简化初始条件：α1（0）＝0；β1（0）＝10。根据初始条件，求得通解为

式（7）描述了陀螺在阶跃力矩作用后的运动规律，式右侧是陀螺运动微分方程非线性项引起的力矩。由式（7）可知：在陀螺无阻尼时，与章动具相同频率ωn的周期力矩引起陀螺的强迫振动并且诱发的力矩很小，故陀螺总存在阻尼使之中和；频率为章动频率高倍的周期谐振力矩，这些高次谐波产生的振动幅值很小，因此无阻尼时影响亦不大。式（7）第二式最右端有一常数项，此常数项将造成陀螺的漂移。忽略高次谐波力矩，近似求得漂移角速度

由式（8）可知：陀螺在受到阶跃力矩或冲击后，除按章动频率及高次谐波频率高频振动外，还会发生角速度为常值的漂移，此即章动引起的漂移误差。由式（8）可发现：漂移误差的角速度与陀螺偏角成正弦相关关系，与陀螺偏角的初值β0的平方成正比关系，且与导引头动力随动陀螺万向支架的内外环质量有关。

由图1可知：在稳态下陀螺呈现出复杂的运动规律，可直观认为是章动频率振动与章动频率高倍频振动的叠加。由图2可知：陀螺在非零初始的条件下存在一定漂移。由此表明，本文认为章动引起漂移的分析正确。

2.1.2 摩擦力矩引起的进动误差

当动力随动陀螺转子在万向支架的内外环转动过程中，由于陀螺转子与各部件接触，特别是在滚珠轴承等部件中，会产生摩擦力矩，摩擦力矩是动力随动陀螺干扰力矩的主要来源。摩擦力矩由各接触部件相互运动而产生，其大小与接触的接触面积、正压力、摩擦因数和偏角等有关，且其方向与转动方向有关。因陀螺内部结构的相互转动有随机性，故摩擦因数的大小和方向亦经常变动，动力随动陀螺的摩擦力矩是一个随机干扰量，其引起的零漂误差和进动误差也是一个随机的量而无法补偿。

2.1.3 非等弹性力引起的进动误差

在便携红外导弹的飞行段，导弹变加速度运动时将带动基座的变加速运动，此时影响陀螺进动误差的因素还有由非等弹性力矩引起的陀螺误差。设当万向支架的加速度为零时，动力随动陀螺转子的重心与万向支架中心重合。当万向支架加速运动时将会产生与加速度方向相反的惯性力作用于重心使重心产生偏移［7］。如导引头中的动力随动陀螺结构在各方向上为等弹性结构，此时陀螺转子的重心刚好沿惯性力作用方向偏离支架中心，由于惯性力作用线通过支架重心，对内、外环支架的力矩为零，不会造成误差。但工程中由于动力随动陀螺结构的复杂性很难实现结构的等弹性，此时重心偏移不再沿惯性力的作用方向。由于惯性力作用线不再通过支架中心，惯性力就会产生对支架中心的力矩，从而引起误差，如图3所示。

由于动力陀螺结构有多个部件复杂的质系，非等弹性力矩的计算非常困难。为简化计算考虑动力随动陀螺内外环均采用高强度合金支撑，与转子相比其重量很轻但刚度很大，在惯性载荷作用下变形很小。本文采用以下近似：假定陀螺的内外环为绝对刚性，忽略陀螺内外环的质量及变形；陀螺的重量集中于转子上，支撑陀螺转子的轴承沿径向和轴向为弹性系数不同的轴承，刚度系数分别为Cx，Cz。因动力随动陀螺的质量主要集中于转子，当万向支架以加速度a运动时，有惯性力Q＝－ma作用于转子的质心产生位移

式中：m为陀螺转子质量；i，k为陀螺转子坐标系与转子轴垂直的两个方向的单位矢量；ax，az为转子两个坐标矢量中加速度；Qx，Qz为转子x、z轴向的惯性力。由于各方向刚度不等，质心偏移r的方向与惯性力矩的方向不会重合，惯性力Q对支架重心产生力矩

式中：θ为加速度与z轴间的夹角。在此力矩下，陀螺的偏差

由式（11）可知：动力随动陀螺的结构非等弹性引起的陀螺误差，与陀螺万向支架即弹体加速度的二次方程成正比例关系。

2.2 稳速力矩和进动力矩耦合引起的控制误差

由文献［8］可求得在转子坐标系中，当转子轴与弹体轴间存在偏角时，稳速线圈和进动线圈对在转子坐标系abs对转子的作用力分别为由转子磁场P与线圈磁场B间的感应力为其矢量积，可得

式中：Kt为基准线圈电流的力矩系数；It为基准线圈旋转电流；KI为进动线圈电流力矩系数；I0为与目标视线角速度成比例的进动电流幅值；v为线圈分布角；α，β为转子坐标系和弹体坐标系的欧拉角，且cos＝cosαcosβ。此处：

其中：Ω为陀螺转子的角速度；R＝sinβcosαsinθsinαcosθ；T＝sinβcosαcosθ＋sinαsinθ。

式（13）中，sin（2Ωt）与cos（2Ωt）在一个积分周期内数值为0，故进动力矩产生作用在一个周期内可抵消为零。简化式（13）可得

式（14）中，前两项是进动力矩轴向分量，可合成为力矩P0kBi0cos／2，故的存在使进动力矩变小；末项KII0（sinαcosθ＋sinβcosαsinθ）／2沿陀螺自转轴为陀螺干扰力矩。稳速线圈的作用是保持转子按一定的角速度转动，进动线圈的作用通过是控制线圈电流让转子进动从而跟踪目标。由式（14）可知：存在偏角时进动线圈的力矩会使陀螺转子的转速改变，而稳速线圈的力矩也会影响陀螺的进动。

3 导引头位标器误差控制机理

3.1 漂移误差调控机理和过程

由章动漂移角速度式（8）可知：漂移角速度与陀螺内外环的质量有关，漂移误差的角速度与β0的正弦值成正比，与β0的平方成正比。为减少章动引起的漂移提高导引头动力随动陀螺的精度，可用以下方法：使β0尽量小，因动力随动陀螺导引头的光学系统工作的角度范围较大，故这较难实现；减小内外环质量，从而减小内外环转动惯量，当内外环质量可忽略不计时章动引起的漂移误差亦可忽略不计；尽量减小陀螺阶跃力矩后的初始速度。

3.2 工艺误差调试机理

工艺误差包括质心偏心工艺误差、非等弹性力误差和摩擦力矩误差等。其中：部分是无法根本消除而只能通过调整陀螺结构和通过零部件工艺以减小，如非等弹性力和摩擦力矩的误差只能通过改善零件制造工艺减少。对质心偏心的误差，可通过调试减少，具体包括动平衡调试、位标器漂移调试和位标器扰动调试。调试原则为：先调试部件再调试总体；总体调试亦遵循由内及外的原则，先调试影响大的误差项，然后在保证大的误差项调试结果不变的情况下，再进行小误差项调节。导引头陀螺调试顺序如图4所示。

经调试，可使陀螺的质心与旋转轴心重合，陀螺质心在纵向（z向）与支架轴心重合，但由于固定质心调节陀螺转轴与进动轴重合的过程中，旋转轴心（质心）与支架轴心可能存在一定的偏差。由于质心固定、轴向固定，无法再通过调试消除此项误差，仅能通过设计或后期补偿以减小误差提高精度。

3.3 控制力矩耦合偏差消除方法

由本文分析可知：当陀螺转子轴与弹体轴存在一个偏角时，控制陀螺的进动力矩与保持转子旋转的旋转力矩会相互耦合，这对系统的跟踪能力等性能有很大影响。对偏角形成的偏差文献［9］提出力矩补偿方法，即利用偏角线圈的输出信号构造补偿信号，如图5所示。图5中：Ku，K1，KH分别为系统控制器、功率放大器和力矩器的放大倍数；K为位标器的恢复力矩系数；K′为人工补偿环节。只要满足K＋K′＝0，即可消除偏角的影响。

4 结束语

本文用拉格朗日第二类方程法，建立了红外导引头动力随动陀螺完备的动力学方程，并基于此分析了导弹受到阶跃力矩或冲击后，除按章动频率及高次谐波频率高频振动外，还会发生角速度为常值的漂移误差，漂移误差的角速度与内外环质量和初始的角速度有关。针对引起陀螺误差的非等弹性力矩、摩擦力矩和陀螺制造误差等因素，给出了漂移误差的控制机理和方法。针对偏角造成的误差，定量分析了误差大小与偏角的关系，并给出了一种可行的力矩补偿偏角误差的方案。各种误差来源的解决措施为：对章动引起漂移误差（源于内外环质量），改善工艺、减小内外环质量；对摩擦力矩误差（源于摩擦力矩），减小摩擦力；对非等弹性力引起误差（源于支架挠性），改进万向支架制造工艺；对结构误差（源于质心与原点、转轴与进动轴不重合），动平衡调试、陀螺扰动调试；对偏角控制误差（源于线圈力矩的耦合），控制力矩补偿。

在转台上模拟红外目标视线，对转台施加一个角度，此时偏角大小固定，动力随动陀螺系统进动稳定后的跟踪信号幅值反映了系统的偏差［10］。在模拟转台上，用本文的动力随动陀螺系统改进工艺、平衡调试和力矩补偿前后的输出信号特性见表1。

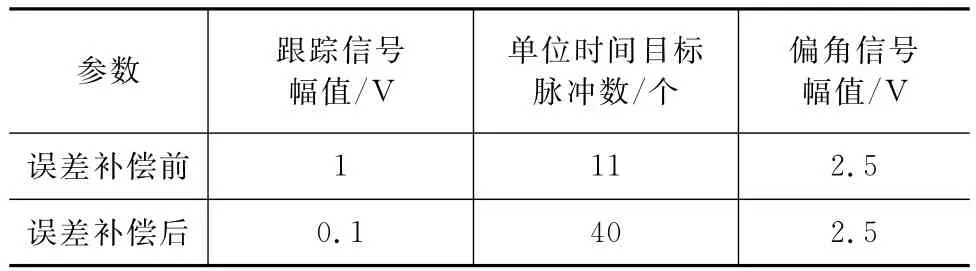
表1 误差补偿前后系统输出特性Fig.1 Output of system before and after compensation

由表1可知：经误差补偿后跟踪信号的幅值明显变小，说明此时陀螺系统的误差变小；同时补偿后的单位时间内输出脉冲数增多，玫瑰线光机扫描系统可描到更多的红外脉冲信号，表明陀螺转子轴对红外目标的指向更精准。采用本文的误差抑制措施，不仅可提高进动系统的跟踪精度，减小静差，而且能识别到更多的目标脉冲信号，利于后期抗干扰算法的实现［11］。

［1］ 李伟忠，刘明娜，姚勤.红外成像导引头目标检测误别共性技术综述［J］.上海航天，2015，31（1）：30－35.

［2］ 王纪南.激光陀螺测试方法的研究和误差模型的建立［J］.航空兵器，2004（4）：9－12.

［3］ 张连超.动力调谐陀螺建模与数字化控制问题研究［D］.长沙：国防科技大学，2007.

［4］ 刘延柱.陀螺力学［M］.北京：科学出版社，1986：44－63.

［5］ 陆元九.陀螺及惯性导航原理［M］.北京：科学出版社，1964：19－37.

［6］ 杨洋.非线性偏微分方程几种解法的研究［D］.南京：南京信息工程大学，2011.

［7］ 叶尧卿.便携式红外寻的防空导弹设计［M］.北京：宇航出版社，1996：63－83.

［8］ 赵善彪.红外导引头位标器陀螺的方位效应研究［J］.弹箭与制导学报，2007，27（3）：33－35.

［9］ 李保平.红外导成像导引头总体设计技术研究（一）［J］.红外技术，1995，17（5）：1－6.

［10］ 魏文俭，秦石乔，张宝东，等.某导引头陀螺进动控制理论研究［J］.电光与控制，2008，15（8）：36－39.

［11］ 刘俊辉，单家元，刘永善.动力陀螺式导引头跟踪能力分析［J］.红外与激光工程，2013，421（8）：2209－2215.

Errors Analysis of Dynamical Servo Gyro in IR Guided Weapons

LEI Hao1，YANG Hai－rong1，ZHU Mu1，NIU Sai－sai1，YANG Yao2
（1.Shanghai Institute of Spaceflight Control Technology，Shanghai 201109，China；2.School of Astronautics，Northwestern Polytechnical University，Xi’an 710072，Shaanxi，China）

To reduce error of dynamic servo gyro of seeker for infrared guidance weapon，the gyro errors were analyzed in this paper.The complete dynamical model was established by Lagrangian method.The gyro error was divided into two parts which were drift error caused by non－ideal structure and control error caused by coupling of speed stabilization moment and procession moment.The structure errors were composed of errors caused by nutation，friction moment and unequal elastic moment.The successive approximation method was applied for analysis.It found that the gyro also made an excursion with a changeless angle rate after the gyro－stabilized seeker came in for an impact except for high frequently libration.The angular speed was depended on the initial angular speed and mass of inner and outer ring.The mechanism of errors caused by drift angle，non－balance moment and unequal elastic moment were given.The control and debugging method of main errors of gyro was given.For drift errors，the mass of inner and outer ring should be as small as possible and initial angle speed should be reduced.For process errors，first was component and then was system for debugging，and the large errors should be debugged ahead the small errors.The moment coupling error was compensated by moment compensation.The study is benefit to guidance for error analysis of seeker and design of control system.

infrared seeker；servo gyro；Lagrangian equations；dynamical model；spin magnetic field；azimuth effect；error compensation；drift error；control error

V241.5

A

10.19328／j.cnki.1006－1630.2017.01.014

1006－1630（2017）01－0086－06

2016－06－13；

2016－08－07

国家973计划资助（613271010204）；上海航天科技创新基金资助（SAST2016073）

雷 昊（1989—），男，硕士，主要研究方向为红外制导。