微型导弹命中角度和时间受控的制导方法研究

毕 鹏，夏晓靖，刘益吉，李 伟

（1.上海机电工程研究所，上海201109；2.西北工业大学航天学院，陕西西安710072）

微型导弹命中角度和时间受控的制导方法研究

毕 鹏1，夏晓靖1，刘益吉1，李 伟2

（1.上海机电工程研究所，上海201109；2.西北工业大学航天学院，陕西西安710072）

为提高微型导弹的杀伤力，研究了一种空中发射微型导弹命中角度和时间受控的制导律。建立了微型导弹和目标的相对运动方程组，用变结构控制理论设计了一种对终端命中角度约束的制导律。为保证微型导弹以特定角度命中目标的同时，命中时间也满足要求，在变结构制导律基础上加入了命中时间受控的制导项。在单发导弹和3发导弹同时攻击地面运动目标的两种场景中，对设计的制导律与修正比例导引律进行了仿真，结果表明：设计的制导律弹道曲线更平直，更易适应导弹末段转弯速率有限的条件，在目标有机动干扰时其制导精度更高，且攻击角度满足约束要求；在多弹协同攻击时，设计的制导律可实现多枚导弹在给定时间内以一定命中角度协同打击同一目标。

无人机；微型导弹；制导律；命中角度和时间；变结构控制；协同攻击；滑动模态；制导精度

0 引言

由于无人机本身重量和尺寸的限制，对其机载导弹的设计提出了很高的要求。在此背景下，微型导弹以价格低、重量轻、威力大、精度高的特点成为精确制导武器的一个新的发展方向，典型代表是美国的长钉导弹。在攻击地面武装车辆时，为提高微型导弹的杀伤力，要求在保证较高打击精度的同时，还需命中角度满足作战要求。对一些装甲厚、反导能力强的目标，为提高突防能力，常需要数架无人机协同发射导弹才能保证消灭目标，这样对命中时间控制也提出了具体要求。目前，针对不同应用背景，提出了多种具有终端落角约束的导引律设计方法，但对终端角度和时间受约束的研究相对较少［1－6］。文献［7］提出了一种新型的攻击时间控制导引律，综合了比例导引律与攻击时间误差反馈控制，并将其用于反舰导弹的齐射攻击，但其攻击目标是固定的，在目标移动情况下可能会受到限制。文献［8］提出了一种同时考虑攻击时间控制和攻击角度控制的二维平面导引律，仿真计算表明能在保证角度和时间的限制下命中目标，验证了设计导引律的正确性，但在工程实际应用时还需进一步研究三维情况下的制导方法。文献［9］采用分阶段的控制方法，给出了一种考虑攻击时间控制和攻击角度控制的三维空间导引律，但其攻击目标是固定的，应用中会存在一定限制。文献［10］在三维空间导引动力学与运动学模型的基础上，研究了导弹速度方向变化时攻击静止目标的攻击时间与角度控制的制导律。文献［11］针对多导弹编队齐射攻击的时间协同要求，采用攻击时间可控制导律实现了多导弹编队在给定时间协同打击不同目标的任务，但未考虑攻击角度的约束。上述文献的研究大多基于二维攻击平面设计相应的制导律，或打击目标是固定的。本文根据三维空间中的弹目相对运动关系，在命中角度与时间约束的条件下，应用滑模变结构与误差反馈控制，对命中角度和时间受控的制导律进行了研究，并用于攻击机动目标的多导弹协同作战任务。

1 弹目相对运动模型

选取地面坐标系A－xyz：原点A为导弹发射瞬时质心在地面上的投影；Ax轴在水平面内，指向目标为正；Ay轴在包含Ax轴的铅垂平面内并与其垂直，向上为正；Az轴与其它两轴垂直并构成右手直角坐标系。微型导弹和目标的相对运动关系如图1所示。图1中：M为微型导弹；T为目标；r为弹目相对距离；qε为视线高低角；qβ为视线方位角；vM，θM，ψVM分别为微型导弹的速度、弹道倾角和弹道偏角；aM为微型导弹的指令加速度；vT，θT，ψVT分别为目标的速度、弹道倾角和弹道偏角；aT为目标的指令加速度。

三维空间中的弹目相对运动方程可表示为

对式（2）、（3）求导，整理得

2 具有角度约束的变结构制导律

滑动模态可根据需要设计且与对象参数及扰动无关，一方面使变结构制导律对不确定因素的干扰有较强的鲁棒性，另一方面将落点所需姿态纳入滑动模态［12］。

为保证微型导弹命中目标的瞬间，命中角度也满足要求，令

式中：θMf为微型导弹命中时刻期望的弹道倾角。若使状态x1，x3趋于零，则实现了以期望命中角度接近目标的要求；若使状态x2，x4趋于零，则满足了命中目标的要求。

式（12）～（15）对时间求导，得

式中：u1，u2为控制量，且u1＝aMy，u2＝aMz；

式（12）～（15）的终端约束为

式中：tf为要求的命中时间。

制导律需同时满足零脱靶量和命中角度的要求，选取滑模面切换函数

式中：λ为角误差系数，且为正的常数。当s1＝0，s2＝0时，系统处于滑模运动状态，此时导弹可按命中角度要求击中目标。

为保证系统状态能达到滑模，并在到达滑模的过程中有良好的动态特性，取自适应滑模趋近律为

式中：k1，ε1，k2，ε2为大于零的常数。

上述自适应趋近律的优势是：当r较大时，能适应减缓趋近滑模的速率；当r→0时，趋近滑模的速率迅速增加，从而保证微型导弹的打击精度。

式（21）、（22）对时间求导，得

综合式（17）、（18）、（21）～（26），将控制变量aMy，aMz视为未知量，其余皆为已知量，求解方程组得变结构制导律，有

式（28）中含开关函数项，要求控制量进行切换。在实际系统中，控制量的切换不可能瞬时完成，总存在一定的时滞，这就会造成抖动，幅度过大的抖动可能有害。为削弱抖动，可对非连续开关函数进行光滑处理，用高增益函数代替开关函数sgn s，此处δ为小正数。

3 命中角度和时间受控的制导律

基于误差反馈控制方法，攻击时间受控的制导律是指在制导过程中使导弹的命中时间不断趋近所要求的攻击时间，即

式中：t为导弹飞行时间；tgo为剩余飞行时间，且。当Δt＞0时，说明预估的命中时间大于要求的命中时间，需降低导弹的飞行高度从而减小飞行时间；当Δt＜0时，预估的命中时间小于要求的命中时间，需升高导弹的飞行高度，进而增大飞行时间。因此，在具有角度约束的变结构制导律基础上，加入命中时间受控的制导项，则有

式中：τ1，τ2为大于零的常数。

考虑重力补偿，根据式（30）、（31）得在弹道坐标系中表示的法向过载指令为

式中：g为重力加速度。

4 仿真计算

4.1 场景1

微型导弹空中发射攻击地面运动的武装车辆。武装车辆以加速度aT＝25sin（0.5t）m／s2、初速vT＝11m／s作机动，武装车辆质心的起始位置坐标为xT＝3 000m，yT＝1.5m，zT＝0m。取导弹仿真初始参数为：速度20m／s；弹道倾角0°；弹道偏角0°；位置坐标（0，500，0）m。分别用本文设计的制导律和文献［13］具有攻击角度和时间约束的修正比例导引律进行仿真，要求命中目标时攻击角度θMf＝－90°、命中时间tf＝24s。仿真所得弹道曲线和过载分别如图2、3所示。主要参数仿真结果见表1。

由图2可知：xAz平面内两种制导律的弹道曲线差别较大，这是由于目标在xAz平面内以加速度aT作机动运动，导弹的制导系统需不断跟踪观测信息给出制导指令，在目标机动干扰条件下用本文制导律的弹道曲线较文献［13］中修正比例导引律的弹道曲线更平直。由图3可知：在导引末段采用本文制导律的法向过载小于文献［13］制导律的法向过载，能更易适应导弹末段转弯速率有限的条件。通过两个制导律的仿真结果对比可发现：在目标有机动干扰时，用本文制导律的命中精度较文献［13］高1个量级，且攻击角度满足要求。

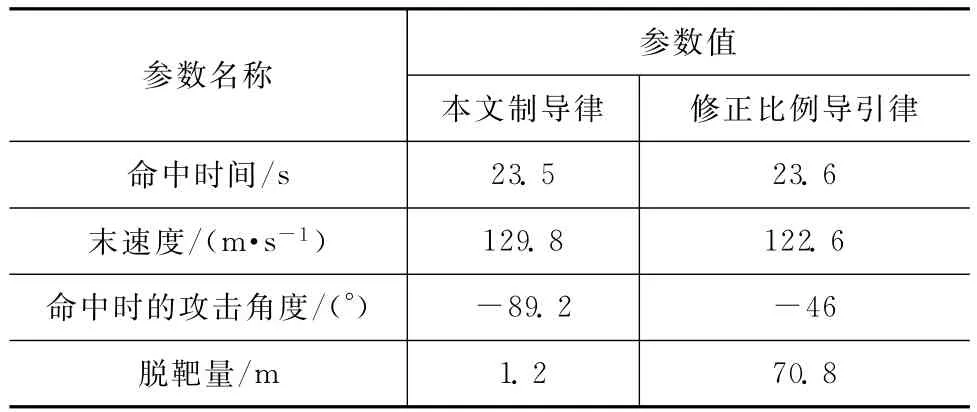
表1 仿真结果Tab.1 Simulation results of main parameters

4.2 场景2

假设3枚微型导弹协同攻击地面运动的武装车辆，用本文设计的制导律进行仿真。目标的仿真初始参数与场景1相同；各导弹的仿真初始参数见表2。微型导弹每隔2s在不同的位置发射一枚，每枚导弹的期望命中时间分别为24，22，20s；各导弹命中目标时的攻击角度θMf＝－90°。仿真所得各导弹弹道曲线、命中角度与剩余时间估计分别如图4、5所示。各导弹主要参数仿真结果见表3。

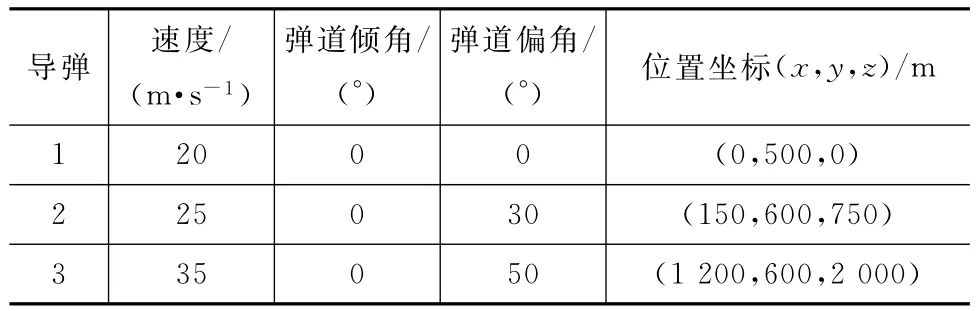
表2 各导弹仿真初始参数Tab.2 Initial simulation parameters of different missiles

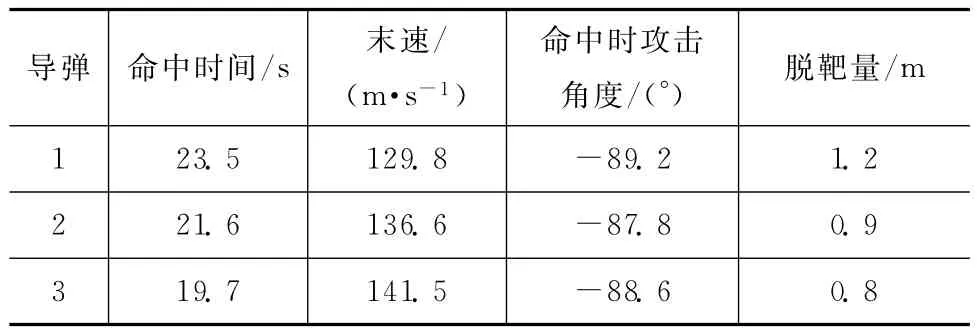
表3 各导弹仿真结果Tab.3 Simulation results of main parameters for different missiles

由图5和表3可知：各枚导弹的命中角度与期望的命中角度误差小于3°，命中时间的误差小于0.5s，获得了较好的攻击效果，实现了多枚导弹在给定时间内以一定命中角度协同打击同一目标的任务。

5 结束语

针对攻击地面机动运动目标，本文对命中角度和时间受控的制导律进行了研究。通过计算机仿真分析，得到了如下结果：在命中角度和命中时间约束的条件下，综合滑模变结构与误差反馈控制方法设计的制导律在攻击机动运动的目标时不仅能保证较高的制导精度而且可满足任务对命中角度和时间的特殊要求；在多枚导弹协同作战的任务中，设计的制导律能保证各枚导弹在同一时间内以一定命中角度协同打击同一目标。

［1］ BAO Y M，JIANG Z C.Design of guidance law of missile in attack with high angle［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34（12）：1375－1378.

［2］ MYUNG－GON Y.Relative circular navigation guidance for three dimensional impact angle control problem［J］.Journal of Aerospace Engineering，2010，23（4）：300－308.

［3］ DAEKU S，BYOUNG－MUN M.Impact angle control guidance law using Lyapunov function and PSO method［C］／／Proc of the SICE Annual Conference.［S.l.］：［s.n.］，2007：2253－2257.

［4］ ASHWINI R，DEBASISH G.SDRE based guidance law for impact angle constrained trajectories［C］／／Proc of the AIAA Guidance，Navigation，and Control Conference and Exhibit.［S.l.］：AIAA，2007：1－16.

［5］ ZHENG Z Z，WANG Y J，WU H.An improved optimal guidance law with impact angle constraints based on genetic algorithms［J］.International Journal of Modeling，Identification and Control，2010，10（1）：94－100.

［6］ MUHAMMAD I，ABDUL R.Analysis of guidance laws for maneuvering and non maneuvering targets［C］／／Proc of the International Bhurban Conference on Applied Sciences and Technology.［S.l.］：［s.n.］，2007：90－96.

［7］ JEON I S，LEE J I，TAHK M J.Impact－time－control guidance law for anti－ship missiles［J］.IEEE Transactions on Control Systems Technology，2006，14（2）：260－266.

［8］ JEON I S，LEE J I，TAHK M J.Guidance law to control impact time and angle［C］／／Proc of International Conference on Control and Automation（ICCA2005）.［S.l.］：［s.n.］，2005：852－857.

［9］ JUNG B，KIM Y.Guidance laws for anti－ship missiles using impact angle and impact time［R］.AIAA，2006－6432，2006.

［10］ 张友安，马培蓓.带有攻击角度和攻击时间控制的三维制导［J］.航空学报，2008，29（4）：1020－1026.

［11］ 邹丽，周锐，赵世钰，等.多导弹编队齐射攻击分散化协同制导方法［J］.航空学报，2011，32（2）：281－290.

［12］ 周荻.寻的导弹新型导引规律［M］.北京：国防工业出版社，2002：8－26.

［13］ 胡凯明，文立华.无人机机载导弹落角和时间控制导引律研究［J］.固体火箭技术，2011，34（4）：413－417.

Study on Impact Angle and Impact Time Control Guidance Law for Micro Missiles

BI Peng1，XIA Xiao－jing1，LIU Yi－ji1，LI Wei2
（1.Shanghai Electromechanical Engineering Institute，Shanghai 201109，China；2.School of Astronautics，Northwestern Polytechnical University，Xi’an 710072，Shaanxi，China）

To improve the killability of micro missile，a control guidance law for the impact angle and the impact time of air－launched micro missiles was studied in this paper.The guidance law with constraints on terminal attacking angle was designed by utilizing the variable structure control theory according to relative dynamic equations of the micro missile and the target.The influence of impact time constraints was also added into the guidance equation，since the demand that the micro missile hit the target with specified angle as well as the impact time would be ensured.The simulation was carried out using control guidance proposed and modified proportional guidance law in two scenarios in which one was only one micro missile and the other was three micro missiles cooperatively.The results showed that the trajectory of the proposed guidance law was smoother than that of modified proportional guidance law，which was suitable to the situation that the turning speed of the missile was limited in the terminal phase.The proposed law had high guidance accuracy for maneuvering target and attacking angle met the constraint requirement.And the proposed guidance law could realize the cooperative attacking the same target with the required impact angle in certain time for many missiles.

unmanned aerial vehicle；micro missiles；guidance law；impact angle and time；variable structure control；cooperative attack；sliding mode；guidance accuracy

TJ765.3

A

10.19328／j.cnki.1006－1630.2017.01.009

1006－1630（2017）01－0056－06

2016－04－15；

2016－06－08

毕 鹏（1986—），男，硕士，主要研究方向为战术导弹总体设计。