基于随机需求的多级库存成本优化模型

王 安



基于随机需求的多级库存成本优化模型

王 安

（平顶山学院，河南 平顶山 467000）

针对多级库存复合而成的一般系统，首先通过分析安全库存与服务水平的关系，给出随机需求下安全库存随前置期和服务水平变化的函数关系；然后结合多级库存的控制特点，建立包含安全库存费用在内的多级库存成本优化模型，并给出遗传算法求解办法。该模型在供应链节点企业总成本最小基础上，确定了最佳订购批量、最佳订购点和服务水平，以及对应的总成本和总利润，进而为各节点企业有效地减少库存量，降低供应链的总成本，提供有力的依据。

随机需求；多级库存；安全库存

0 引言

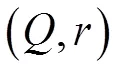
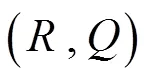
1 变量定义与假设

1.1 符号说明

1.2 模型的假设条件

（1）单位时间内的各节点企业产品需求是互相独立的；

（2）单位时间内的各节点企业产品需求是随机变量，符合正态分布；

（3）前置期的时间是随机变量，并且符合正态分布。

假设订购点前置货物需求量为随机变量，则实际需求就可能超过期望需求，因此为了减少缺货风险，就应该持有一定的安全库存，此时订购点为：

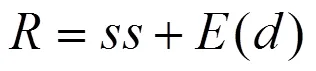
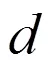
此时，安全库存为:

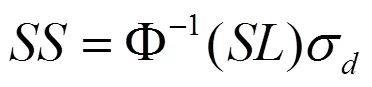
令安全系数为:

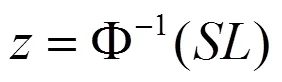
通过正态分布表可以查得常见的服务水平对应的安全系数，利用Matlab进行数据拟合程序，求得服务水平与安全系数的三次多项式函数关系如下：

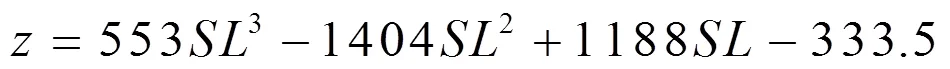
进而，推得安全库存为：

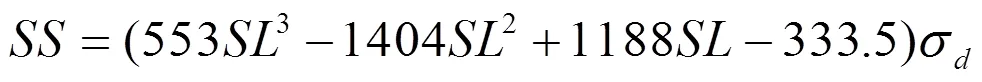
故将（7）代入（6），得：

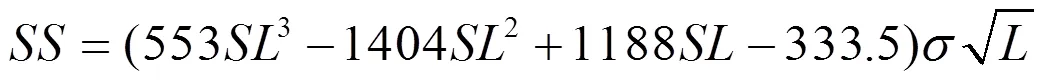
2 多级库存成本优化模型建立与仿真求解

假设单位时间内的各节点企业产品需求是互相独立的；单位时间内的各节点企业产品需求是随机变量，并且符合正态分布；只考虑一种产品的情况；在物品订购中，存在与订购数量无关的固定订购费用；库存系统每级节点运输成本由本级节点企业承担；前置期的时间是随机变量，并且符合正态分布。

2.1 模型建立

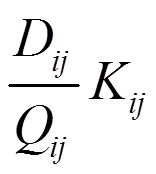
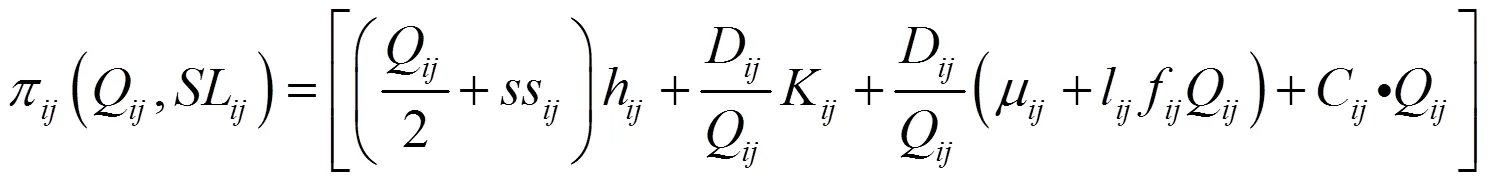
整个供应链的总成本为：

建立以供应链总成本最小为目标的多级库存数学模型如下：

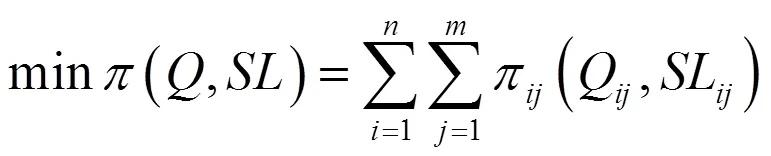
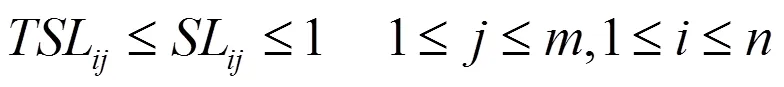
2.2 仿真求解

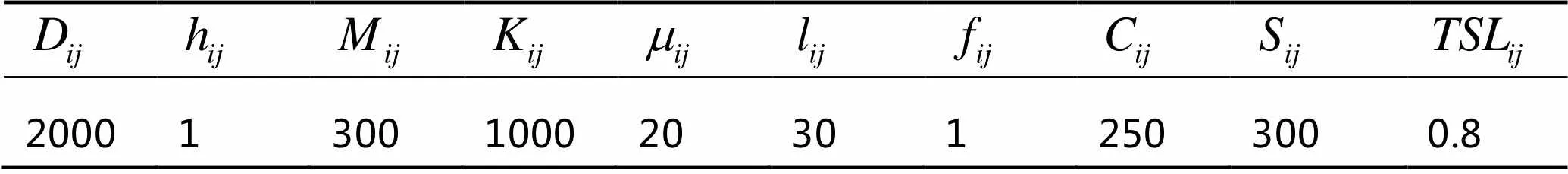
表1 仿真实例参数表

当其他参数不变，仅改变服务水平和订购批量时，企业的服务水平和订购批量会影响企业的年总成本。具体来说，固定服务水平、增加订购批量和固定订购批量、增加服务水平都会使企业的年总成本变化，且前者的影响比后者的影响更为显著。因此这种情况下，企业要降低年总成本，应把注意力放在订购批量的变化上，合理地控制订购批量以保障一定服务水平下成本最低。

3 结论

分析安全库存量与服务水平的关系，并拟合出安全库存和服务水平的函数关系。建立包含安全库存的存储费、订购费、运输费、缺货费用和产品购入成本的库存成本优化模型，并给出该模型的遗传算法求解方法。结合本文所建立的库存优化模型，通过对未来产品需求量的预测，可以求解得到未来时间段内的最佳订购批量、订购点和服务水平，以及采取该管理方法对应的总成本和企业的总利润，这可为企业的管理者制定有效的管理方案提供依据。

（责任编辑王 磊）

[1] 蔡临宁.物流系统规划——建模及实例分析[M].北京:机械工业出版社,2003.

[2] K. Moinzadeh, H. L. Lee. Bath size and stocking levels in multi-echelon repairable systems[J]. Management,1986（32）:1567-581.

[3] A. Svoronos and P. Zipkin. Estimating the performance of multi-level inventory systems[J]. Oper Res,1988（36）:57-72.

[4] R. D. A. Badinelli, model for continuous-review Pull Policies in serial inventory systems[J]. Oper Res,1992（40）:142-156.

[5] 牛海军,孙树栋.多阶段生产/库存系统随机需求的整体库存模型[J].西安电子科技大学学报(自然科学版),2001(5):612-615.

[6] 高峻峻.需求不确定的分销系统最小成本模型[J].东北大学学报(自然科学版),2003(1):87-91.

F274

A

1008–2093(2017)05–0056–04

2017-08-11

王安（1983―），男，河南开封人，硕士，助教，主要从事计算数学和数学模型研究。