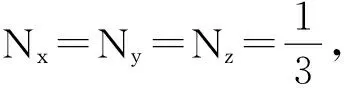均匀外电场中的一般椭球形导体

赵 强 籍万新

(西安交通大学 1理学院；2数学与统计学院， 陕西 西安 710049)

教学经验交流

均匀外电场中的一般椭球形导体

赵 强1籍万新2

(西安交通大学1理学院；2数学与统计学院， 陕西 西安 710049)

根据一个均匀极化的一般椭球形电介质表面的极化电荷的分布规律与一个处在均匀外电场中具有相同形状的导体椭球表面上感应电荷的分布规律的相似性，通过先求出均匀极化椭球表面上极化电荷的分布规律，然后用类比的方法给出了一个处在均匀外电场中具有相同形状的一般椭球形导体表面上电荷的分布规律。

一般椭球； 面密度； 珀塞尔的观点； 退极化因子

文献[1]讨论了均匀外电场E0中旋转椭球形导体表面的感应电荷的分布规律，本文则讨论均匀外电场E0中一般椭球形导体表面的感应电荷的分布规律。和文献[1]一样，本文也采用类比的方法，目的仍是为了避开拉普拉斯方程复杂的求解过程，用普通物理的方法解决问题，从而最大限度地突出问题中的物理图像。

我们暂时抛开导体椭球问题不谈，首先考虑一个与导体椭球形状完全相同且沿主轴方向均匀极化的电介质椭球。设该电介质椭球面在直角坐标系中的方程为

(1)

若此电介质椭球的极化方向沿z轴的正方向，并且极化强度为P，则此电介质椭球表面的极化电荷密度为

(2)

式(2)中的n为电介质椭球表面的单位法向矢量，其具体表达式为

(3)

将式(3)代入式(2)中，有

(4)

根据E.M.珀塞尔的观点[2]，一个均匀极化的电介质椭球，其表面的极化电荷将在椭球的内部产生一个与极化方向完全相反的均匀的退极化场。在电介质椭球沿z主轴均匀极化的情况下，E.M.珀塞尔的观点可以用如下的式子来表示

(5)

式(5)中的Nz可称为电介质椭球的z主轴的退极化因子。在式(5)中将P除以ε0是处于量纲上的考虑，这样可使Nz为一无量纲的纯数，其数值完全由椭球的形状来决定。将式(5)代入式(4)，有

(6)

根据对称性，若电介质椭球的极化方向分别沿x主轴和y主轴时，极化电荷的面密度与退极化场之间的关系分别为

其中Nx、Ny分别是电介质椭球x主轴和y主轴的退极化因子，同样是由椭球的几何形状决定的无量纲纯数。

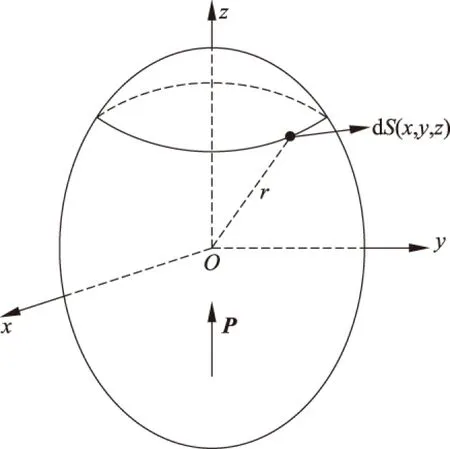
图1 沿z主轴均匀极化的电介质椭球

下面求出式(6)～式(8)中的3个主轴的退极化因子Nz、Nx、Ny的具体表达式。如图1所示，电介质椭球沿z主轴方向均匀极化，极化强度为P。在椭球表面任意一点(x,y,z)处选一小面元dS，面元dS上的极化电荷dq′在椭球中心O处产生的元场强在z轴上的分量为

椭球表面上所有的极化电荷在椭球中心产生的场强在z轴上的分量为(根据E.M.珀塞尔的观点，此场强也是椭球内任意一点的退极化场的场强)

(9)

若用式(9)给出Nz的具体表达式，需将式(9)中的直角坐标作椭球坐标变换，即

(10)

根据微分几何的知识，椭球面法线的方向数为

椭球的表面积微元为

(11)

式(2)在椭球坐标下的形式为

(12)

将式(10)～(12)代入式(9)，有

(13)

比较式(13)和式(5)，有

(14)

式(14)就是电介质椭球的z主轴的退极化因子。从式(14)可以看出Nz完全由椭球的几何形状确定，即由椭球的3个主轴的半长度a、b、c确定的一个无量纲纯数。

同样的道理，可求出Nx和Ny的具体表达式为

实际计算表明：0

Nx+Ny+Nz=1

(17)

若a≠b≠c，式(14)～式(16)无法给出关于a、b、c的解析表达式。但是由于有了计算机这一强大武器，Nx、Ny、Nz是否可表示为解析形式并不重要。只要将a、b、c的具体数值代入式(14)～式(16)中，用计算机可以很容易地求出任意精确度的数值。为了给大家一个直观印象，笔者将4组a、b、c为特定值时所对应的Nx、Ny、Nz的值列于表1，供读者参考[3]。

表1 退极化因子和椭球形状之间的关系

至此，分别沿3个主轴方向均匀极化的电介质椭球表面的极化电荷的面密度与其退极化场之间的关系已完全研究清楚。现在讨论处在均匀外电场E0中的与电介质椭球形状完全相同的导体椭球问题。根据导体的静电平衡条件，当导体椭球放到均匀外电场中时，导体表面的感应电荷将在导体内部产生一个与E0完全相反的均匀电场E(E=-E0)将E0抵消掉。当导体椭球内的感应电场E正好和同形状的均匀极化椭球内的退极化场E′相等时，根据静电场的唯一性定理，导体椭球表面的感应电荷的分布规律和同形状的电介质椭球表面的极化电荷的分布规律完全一样，也应有式(6)～式(8)的形式。因此，当外电场E0分别沿导体椭球的x主轴、y主轴及z主轴时，导体椭球表面上感应电荷的面密度分别为

式(18)～式(20)中的Nx、Ny、Nz的具体表达式仍由式(15)、(16)、(14)给出。

最后，若将导体椭球以任意姿式放进外电场E0中，这时E0与导体椭球的三个主轴的夹角分别为α、β、γ。在这种情况下，我们可将E0沿导体椭球的三个主轴进行分解，根据静电场的叠加原理和静电场的唯一性定理，最后的结果为

σ=σxcosα+σycosβ+σzcosγ

(21)

式(21)中的σx、σy、σz分别由式(18)～式(20)给出。

[1] 赵强，曲哲.均匀电场中的椭球形导体[J].物理与工程， 2016，26(1)：23-25. Zhao Qiang, Qu Zhe. Ellipsoidal conductor in uiform electric field[J]. Physics and Engineering, 2016, 26(1): 23-25. (in Chinese)

[2] 珀塞尔E.M..电磁学[M].伯克利物理教程.第2卷.南开大学物理系，译.北京：科学出版社，1979：406.

[3] 朱旭,李换琴,籍万新.MATLAB软件与基础数学实验[M].西安：西安交通大学出版社,2008.

■

ELLIPSOIDAL CONDUCTOR IN UNIFORM ELECTRIC FIELD

Zhao Qiang1Ji Wanxin2

(1School of Science,2School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an Shaanxi 710049)

Based on the similarity between the distribution of induced charges on the surface of uniformly polarized dielectric ellipsoid and that on a conducting ellipsoid in external electric field with the same shape, we give the distribution of the charges on the surface of a conducting ellipsoid in external electric field through their analog, after achieving the distribution of induced charges on the surface of uniformly polarized ellipsoid with the same shape.

ellipsoid; surface density; Purcell; depolarization factor

2016-04-22

赵强，籍万新. 均匀外电场中的一般椭球形导体[J]. 物理与工程，2017，27(1)：65-67.