滚轮和型筒表面形貌对卧式离心铸造机振动性能的影响

李柳湘,李正美,黄龙文,安 琦

(华东理工大学 机械与动力工程学院,上海 200237)

离心铸造机工作时型筒会发生振动,特别是炉管离心铸造机,型筒长度方向尺寸较大,振动对产品质量的影响不可忽略.Chirita等[1-3]研究了振动对离心铸造产品质量的影响.在文献[1]中,振动对铸件的机械性能(断裂强度)有负面的影响；文献[2-3]也对型筒振动进行了研究,而得出的结论却有所不同.从这些研究来看,离心铸造机型筒振动的影响因素十分复杂,尚无定论.

在直接作用于转子上的激励力中,最普遍的是不平衡离心力[4-6],另外,还有在电机中转子受到的电磁激励[7-8]和在透平机械中转子受到的流体激励[9]等.Avramov[10]用多尺度法研究了单盘转子在非线性支承下，由不平衡离心力引起的响应.Rao等[11]在研究齿轮传动系统动力学响应时，也将不平衡离心力考虑了进去.Meng等[12]用传递矩阵法研究了燃气轮机的离心不平衡响应.Werner[13]建立了弹性支承发电机转子在离心不平衡激励、电磁激励下的振动模型.Benra等[14]建立了污水泵中流体激励力的计算方法,并用有限元法研究了流体激励下系统的振动.Ying等[15]研究了基础激励对涡轮增压器转子动力学性能的影响,结果表明,在基础激励的作用下,转子表现出的动力学性能与无基础激励的情况差别很大.Suzuki[16]建立了基础激励下电磁轴承-转子系统的动力学模型,并提出了一种加速度前馈控制法，减小基础激励引起的振动.Choy等[17]在研究透平机械的动力学特性时考虑了不平衡力、基础激励以及叶片损失的作用效果.

引起离心铸造机振动的原因有很多,包括支承滚轮和型筒的外圆几何误差、型筒转子的不平衡以及型筒的弯曲变形等[18-20].作者在之前的一项工作[21]中,已经研究了型筒转子的质量偏心对离心铸造机振动性能的影响,其他因素的作用并未考虑.到目前为止,在离心铸造机中，由支承滚轮与型筒表面形貌引起的对型筒的激励力以及此激励力对型筒转子振动性能的影响尚未有报道,而研究这部分因素对型筒振动性能的影响十分必要,所以本文将对此进行一些研究工作.

1 动力学模型的构建

如图1所示,滚轮支承卧式离心铸造机的型筒由4个滚轮支承,每个滚轮又由一对滚动轴承支承并固定在底板上,其中一个滚轮通过皮带与电机主轴相连.在离心铸造机工作时,由滚轮与型筒之间的摩擦力驱动型筒高速旋转.

图1 滚轮支承卧式离心铸造机结构示意图Fig.1 Structure diagram of a roller-supporting horizontal centrifugal casting machine

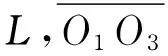
图2 坐标系的建立Fig.2 Reference frame

在图2所示的坐标系下，3个圆的表面轮廓方程如下：

左滚轮:

(1)

右滚轮:

(2)

型筒:

(3)

1.1 滚轮、型筒表面形貌与真实接触

实际上,受加工精度等因素的影响,滚轮与型筒的外表面将不是标准的圆,滚轮与型筒的外轮廓会产生一定的几何粗糙形貌(在公差范围内),这种形貌是随机的.在研究时,可以利用自相关函数法，得到随机的粗糙表面,其基本步骤如下[22]:

(1) 利用计算机生成一个高斯分布白噪声二维随机序列η(x,y),计算其傅里叶变换A(ωx,ωy);

(2) 根据指定的自相关函数R(τx,τy),通过傅里叶变换得到滤波器输出信号的功率谱密度Gz(ωx,ωy),同时确定输入序列的功率谱密度C;

(3) 由式H(ωx,ωy)=[Gz(ωx,ωy)/C]1/2计算滤波器的传递函数;

(4) 利用式Z(ωx,ωy)=H(ωx,ωy)A(ωx,ωy)得到输入序列经过二维滤波器后的输出序列的傅里叶变换Z(ωx,ωy);

(5) 对Z(ωx,ωy)进行傅里叶逆变换得到表面H(ωx,ωy)的高度分布函数z(x,y).

取自相关函数为R(τx,τy)=σ2·exp{-2.3[(τx/βx)2+(τy/βy)2]1/2},这是常用的指数形式的自相关函数,取相关长度为βx=βy=10,表面粗糙度均方根为σ1=σ2=σ3=25 μm,得到随机表面如图3所示.

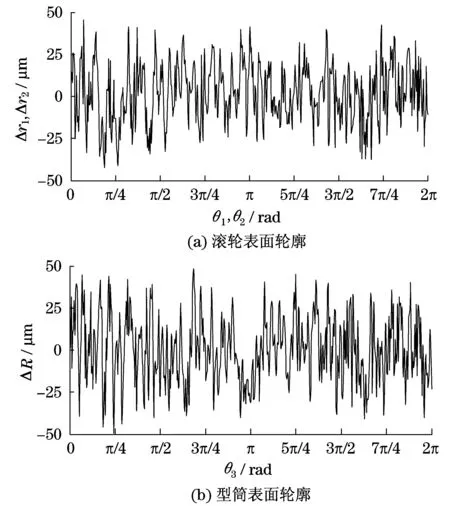
图3 表面轮廓Fig.3 Surface topography

图4中考虑了表面形貌后的真实接触.当考虑两个滚轮和型筒的外表面形貌时,初始时刻支承滚轮和型筒的外圆轮廓可用如下方程描述:

左滚轮:

[x-Δr1(θ1)cosθ1]2+

(4)

右滚轮:

[x-Δr2(θ2)cosθ2-L]2+

(5)

型筒:

(6)

式中:Δr1,Δr2和ΔR分别为左、右滚轮及型筒的表面形貌高度,定义为实际轮廓上的点与理想轮廓上的点之间的距离;θ1,θ2和θ3分别为它们圆周方向的方位角.

图4 滚轮与型筒真实接触Fig.4 Real contact between rollers and mould

假设滚轮与型筒之间的相对运动为纯滚动,那么经过时间t后,左、右滚轮转过的角度相等,为ω1t,型筒转过角度为ωt,其中ω1和ω分别为滚轮和型筒的转动角速度,方向如图4所示,ω1和ω之间存在关系ω=ω1r/R.

令

f(X,Y,r,Δr,θ)=[X-Δr(θ)cosθ]2+

[Y-Δr(θ)sinθ]2-r2

那么t时刻滚轮和型筒的外轮廓方程如下：

左滚轮:

f(xcosωt-ysinωt,xsinωt+

ycosωt,r0,Δr1,θ1)=0

(7)

右滚轮:

f(xcosωt-ysinωt-L,xsinωt+

ycosωt,r0,Δr2,θ2)=0

(8)

型筒:

f(xcosωt-ysinωt-a3,xsinωt+

ycosωt-b3,R0,ΔR,θ3)=0

(9)

1.2 滚轮与型筒接触点的计算

|min[y3(x)-y1(x)]|=0

|min[y3(x)-y2(x)]|=0

(10)

1.3 激励力的计算和型筒转子动力学方程

(11)

式中:m为型筒转子的质量.

离心铸造机型筒是一个连续质量转子,本文选用传递矩阵法对其进行动力学性能计算.首先用集总参数法将转子离散成n个只计质量不计厚度的圆盘和弹性无质量轴段的组合,如图5所示,第n个轴段,其长度ln=0.

图5 转子离散化Fig.5 Discrete model of the mold rotor

对第i个圆盘进行受力分析,如图6所示.根据受力分析可写出圆盘运动微分方程为

(12)

(13)

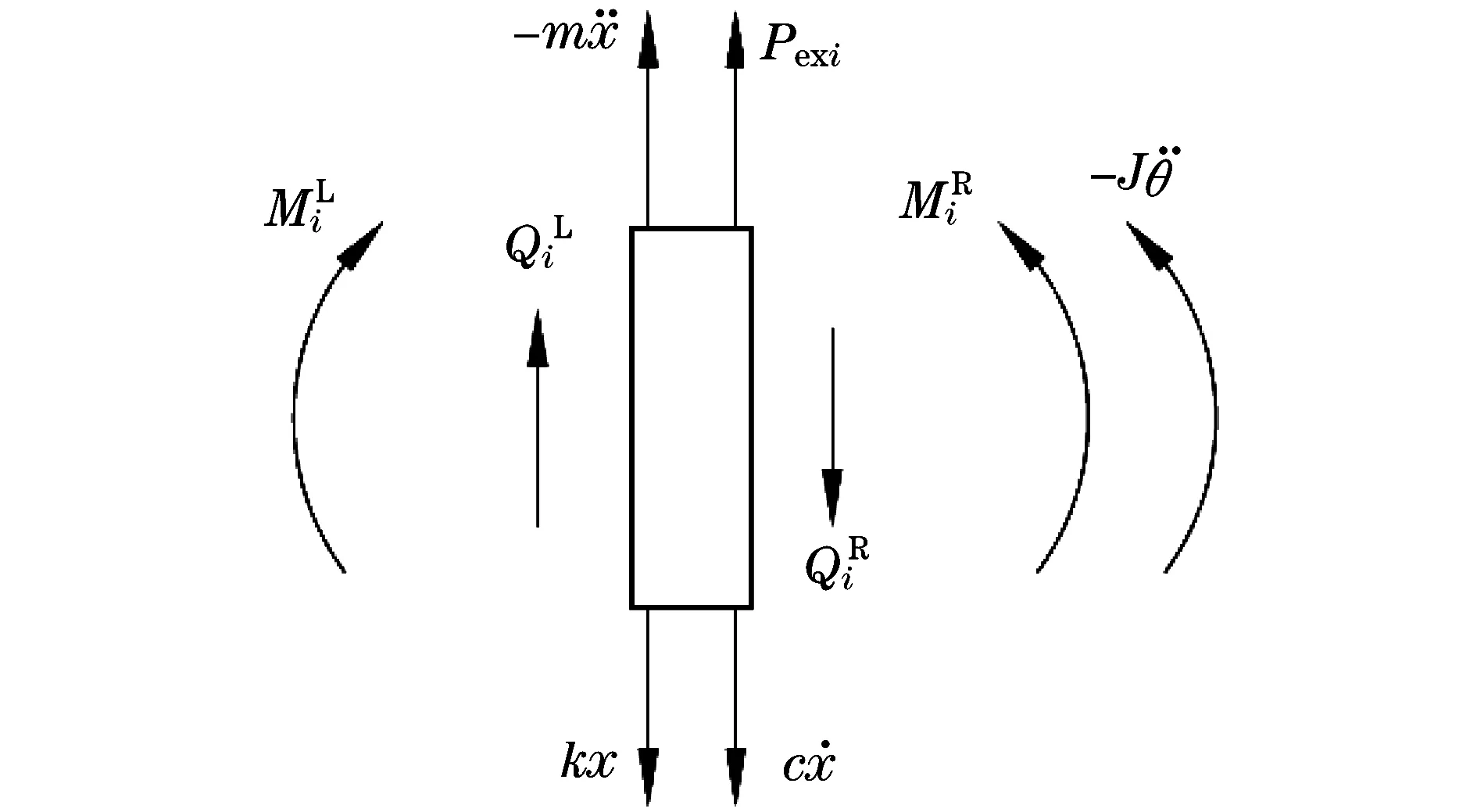
图6 圆盘受力分析Fig.6 Force balance of node

在式(12)和式(13)中,m和J分别为圆盘的质量和转动惯量,k和c分别为支承刚度和阻尼,其计算方法参见文献[21],ωs为激励力的频率.式(13)可以简记为

(14)

第i个轴段两端的传递关系[23]为

(15)

记为

(16)

(17)

并根据边界条件,最后得到

(18)

上述计算方法针对的是外激励为简谐激励的情况,但是一般情况下,支承滚轮与型筒表面形貌引起对型筒的激励Pex(t)和Pey(t)是周期非简谐激励,这种情况下,需要用Fourier展开后得到简谐激励的叠加.用上述方法分别计算每一项引起的响应,再根据叠加原理将每一项引起的响应叠加,便可得到总的响应.

2 算例分析

本文以卓然(靖江)设备制造有限公司的J523型卧式滚轮离心铸造机为例,研究支承滚轮与型筒表面形貌对离心铸造机振动性能的影响.表1为该型号离心铸造机各零部件尺寸以及装配尺寸.由文献[21]可得每个支承处的刚度和阻尼分别为Kx=7.42×108N/m,Cx=5.23×103N·s/m,Ky=6.38×108N/m,Cy=4.50×103N·s/m.计算时,将离心铸造机型筒划分为101个单元,即节点数n=101.

表1 离心铸造机尺寸Tab.1 Dimensions of J523 type roller-supporting horizontal centrifugal casting machine

考虑滚轮和型筒的加工方法,可知其表面粗糙度(Ra)在1.6～25 μm范围内,本文进行算例研究时Ra在这一范围内取值.图7给出了表面粗糙度引起的激励力最大幅值随Ra的变化规律.可以看出,当Ra增大时,激励幅值随之近似线性增加.另外,在相同的转速和Ra下,水平x方向的激励幅值小于垂直y方向,这是由于左、右两侧接触引起的激励力在水平方向的分量方向相反,一部分激励力被抵消掉了,而在垂直方向的分量方向相同.

图8给出了其中3个节点的最大振幅随激励力的变化规律,其中1号节点位于型筒端部,21号节点位于滚轮支承处,51号节点位于型筒中间部位.可以看出,最大振幅随Ra的变化趋势与图 7中激励幅值随Ra的变化趋势一致,Ra值较大时,引起的振幅也较大,两者之间的关系呈近似线性关系.

图9为滚轮转速Ω1在0～2 000 r/min范围内1号节点在不同粗糙度下的幅频响应.可以看出,在不同的粗糙度下,发生较大振幅的转速基本相同.在该算例中,滚轮转速Ω1约为600,800,950,1 550和1 900 r/min时,转子振幅较大.

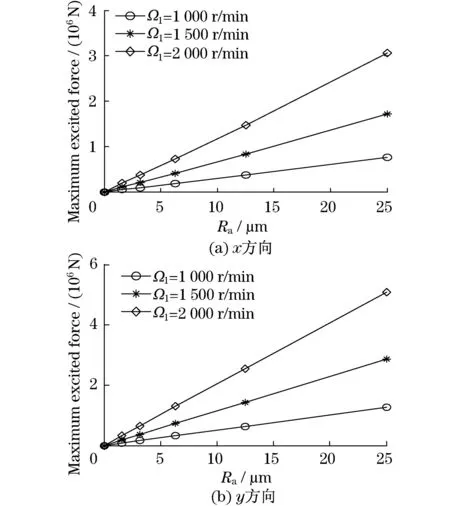
图7 最大激励力随Ra变化Fig.7 Maximum excited forces change with Ra

图8 节点最大振幅随Ra变化Fig.8 Maximum amplitudes change with Ra

图10给出了Ω1=1 500 r/min时不同Ra值下的转子形态.从图10可以看出,在相同时刻,不同Ra值下的转子形状相似,不同之处在于振幅大小.图 11为Ω1=1 500 r/min时不同Ra值下的节点运动轨迹(1号节点),节点运动轨迹则更直观地反映了Ra对振幅大小的影响:Ra值越大时,节点中心的运动范围也越大,即振幅越大.

图9 幅频曲线(1号节点)Fig.9 Amplitude-frequency curves(No.1 node)

图10 不同Ra下的转子形态(Ω1=1 500 r/min)Fig.10 Shapes of mould rotor under different Ra(Ω1=1 500 r/min)

图11 不同Ra下型筒中心运动轨迹(Ω1=1 500 r/min,1号节点)Fig.11 Orbits of node under different Ra(Ω1=1 500 r/min,No.1 node)

3 结论

(1) 离心铸造机的支承滚轮和型筒的微观表面形貌会对型筒转子形成激励,进而对其振动性能产生影响.本文用自相关函数法模拟了滚轮和型筒随机的表面形貌,给出了计算滚轮与型筒接触点坐标的计算方法,求得型筒转子受到支承滚轮的激励力,再结合传递矩阵法,构建了能够在考虑支承滚轮与型筒表面形貌的情况下,对型筒振动性能进行计算的方法.

(2) 通过算例,研究了不同表面粗糙度值对型筒转子振动性能的影响,结果表明:粗糙度引起的激励力以及节点最大振幅随粗糙度的增大近似线性增大;粗糙度不同时,幅频响应中发生较大振幅的转速基本相同;在同一转速下,相同时刻转子的形态相似,但振幅随粗糙度的变化而变化;型筒中心运动轨迹范围随粗糙度的增大而增大.

[1] CHIRITA G,STEFANESCU I,SOARES D,et al.Effect of gravity/vibration/centrifugal process on mechanical properties of an Al-Si alloy[J].Materials Science Forum,2008,587/588:395-399.

[2] CHIRITA G,STEFANESCU I,SOARES D,et al.Centrifugal versus gravity casting techniques over mechanical properties[J].Anales de Mecánica de la Fractura,2006,I:317-322.

[3] CHIRITA G,STEFANESCU I,BARBOSA J,et al.On assessment of processing variables in vertical centrifugal casting technique[J].International Journal of Cast Metals Research,2009,22:382-389.

[4] YADAV H K,UPADHYAY S H,HARSHA S P.Study of effect of unbalanced forces for high speed rotor[J].Procedia Engineering,2013,64:593-602.

[5] HARSHA S P.Nonlinear dynamic analysis of an unbalanced rotor supported by roller bearing[J].Chaos,Solitons and Fractals,2005,26:47-66.

[6] TIWARI M,GUPTA K,PRAKASH O.Dynamic response of an unbalanced rotor supported on ball bearings[J].Journal of Sound and Vibration,2000,238:757-779.

[7] BELMANS R,VANDENPUT A,GEYSEN W,et al.Calculation of the flux density and the unbalanced pull in two pole induction machines[J].Electrical Engineering,1987,70:151-161.

[8] WERNER U.Theoretical rotor dynamic analysis of two-pole induction motors regarding excitation due to static rotor eccentricity[J].Archive of Applied Mechanics,2011,81:241-262.

[9] SIEKMANN H,STARK M.Analytical and experimental study of the hydrodynamic unbalance of single-vane impellers[C]∥3rd Int Symposium on Transport Phenomena and Dynamics of Rotating Machinery(ISROMAC-3),Honolulu,Hawaii,USA.1992:D-28A.

[10] AVRAMOV K V.Asymptotic analysis of the forced vibrations of a one-disc rotor on a non-linear flexible base[J].Journal of Mechanical Engineering Science,2015,224:1593-1604.

[11] RAO J S,CHANG J R,CHOI S T.Dynamic behavior of geared rotors[J].Transactions of the ASME,1999,121:494-503.

[12] MENG C,SU M,WANG S B.An investigation on dynamic characteristics of a gas turbine rotor using an improved transfer matrix method[J].Journal of Engineering for Gas Turbines and Power,2013,135:122505.

[13] WERNER U.Theoretical vibration analysis of soft mounted electrical machines regarding rotor eccentricity based on multibody model[J].Multibody System Dynamics,2010,24:43-66.

[14] BENRA F K,Dohmen H J,Schneider O.Calculation of hydrodynamic forces and flow induced vibrations of centrifugal sewage water pumps[C]∥4th ASME_JSME Joint Fluids Engineering Conference,Honolulu,Hawaii,USA.2003:603-608.

[15] YING G C,MENG G,JING J P.Turbocharger rotor dynamics with foundation excitation[J].Archive of Applied Mechanics,2009,79:287-299.

[16] SUZUKI Y.Acceleration feedforward control for active magnetic bearing systems excited by ground motion[J].IEE Proceedings Control Theory and Applications,1998,145:113-118.

[17] CHOY F K,PADOVAN J,QIAN W.Effects of foundation excitation on multiple rub interactions in turbomachinery[J].Journal of Sound and Vibration,1993,164:349-363.

[18] KHARICHA A,BOHEK J,LUDWIG A,et al.Vibrations induced flow in a horizontal centrifugal casting[C]∥Symposium on CFD Modeling and Simulation in Materials Processing Held during the TMS Annual Meeting and Exhibition,Orlando,US.Pennsylvania:TMS,2012:227-234.

[21] LI L X,JIANG Y Y,LI Z M,et al.Study on the vibration characteristics of a roller-supporting horizontal centrifugal casting machine[J].Journal of Multi-body Dynamics,2016，230(1)：99-109.

[22] 陈辉,胡元中,王慧,等.粗糙表面计算机模拟[J].润滑与密封,2006(10):52-59.

CHEN H,HU Y Z,WANG H,et al.Computer simulation of rough surfaces[J].Lubrication Engineering,2006(10):52-59.

[23] GENTA G.Dynamics of rotating systems[M].New York:Springer,2005.