煤炭类期货收益率分布拟合与风险度量

李百吉，杨子铭，孔德泰

(中国矿业大学(北京)管理学院，北京 100083)

煤炭类期货收益率分布拟合与风险度量

李百吉，杨子铭，孔德泰

(中国矿业大学(北京)管理学院，北京 100083)

近年来，受煤价下跌的影响，煤炭类期货价格波动剧烈，随之而来的风险也不断加大。在这样的市场环境下，原有的正态分布的VaR模型已很难准确度量煤炭类期货的价格波动风险。因此，如何更好地更准确地度量煤炭类期货价格风险成为当前亟待解决的问题。本文在利用VaR模型的基础上，借助K-S检验逐类筛选其他可替换正态分布的假设，以更好、更准确地提高风险度量精度。K-S检验结果显示，煤炭类期货收益率服从双曲线分布；概率密度曲线图和Q-Q图显示，双曲分布比正态分布拟合效果更优；VaR计算与比较结果显示，双曲线分布VaR比正态分布VaR更接近历史VaR，且焦煤VaR大于动力煤VaR。因此，基于双曲线分布的VaR模型更适于投资者度量煤炭类期货风险，投资焦煤期货的风险大于投资动力煤。

煤炭类期货；VaR；分布拟合；正态分布； 双曲线分布

1 研究现状与存在问题

随着实证研究方法的发展，金融计量学家发现：绝大多数金融时间序列数据的分布均存在尖峰、厚尾特征，并不服从正态分布假设。因此，原有的正态分布的VaR模型的风险度量精度受到了怀疑。为提高VaR模型的风险度量精确度，国内外学者做了大量卓有成效的工作，提出了众多的改进方案。这些改进工作主要沿两条路径展开：一是对样本数据集的处理，即利用适当的转换函数，将不符合正态分布的初始样本数据集变换成基本满足正态分布的计算样本数据集，然后用变换后的样本数据集来估测VaR[1]；二是针对正态分布假设偏差的修正，其中包括不考虑分布的方法(如蒙特卡洛模拟法)和更换分布假设的方法(如Logistic分布、t分布、GED分布等)。

综合现有相关研究成果不难发现，利用转换函数处理样本数据集的方法需要根据经济周期的不同阶段选择不同的转换函数，操作繁琐且对数学知识的要求较高；蒙特卡罗模拟法计算量大，且可能因价格随机过程选择不当而招致失败。然而，针对正态分布假设偏差的修正只需找到合适的分布假设即可在原VaR模型的基础上提高风险度量精度，相比其他方法操作简便，易于理解。因此，本文在VaR模型的基础上，尝试以双曲线分布假设替换正态分布假设，以提高风险度量精度。

在修正模型假设方面，国内外学者做了如下工作。Mandebrot[2]提出用稳定分布假设代替正态分布假设，而Officer[3]、kgiray和Booth等[4]提供了反对稳定分布假设的证据，何建敏等[5]对中国证券市场收益率分布的研究也证实了稳定分布的尾部通常比实际分布更厚。arndorff-Nielsen[6]引入广义双曲分布，并在金融领域得到成功应用。Eberlein和Keller[7]率先将它的一个子类“双曲线分布”应用到金融领域。Barndorff-Nielsen[8]基于正态逆高斯分布对股票收益进行了研究。Prause[9]，arndoff-Nielsen和Shepard[10]和McNeil[11]等对GH分布的极限分布“偏t分布”做了研究。在国内，邹健[12]用广义双曲线分布研究了普通欧式期权的定价问题。郭海燕和李纲[13]将双曲线分布和NIG分布应用于中国证券市场风险度量之中。

上述研究成果都为进一步研究风险测度方法奠定了坚实的理论和实证基础，但依旧存在如下不足：①现有研究多数集中于股票市场，将修正过分布假设的VaR模型应用于期货(尤其是煤炭类期货)风险测度的文献极少；②期货风险度量不同于其他金融资产风险度量，需同时度量多空双方的风险。因此，现有多数文献建模时仅度量价格下跌风险却忽视价格上升风险的处理方法不适用于期货类资产；③现有对VaR模型各类分布假设的研究仅对某一分布假设下的VaR值进行计算，缺少对不同分布下VaR值的对比分析。

针对已有研究不足，本文在VaR模型的基础上，借助K-S检验逐类筛选其他可替换正态分布的假设，第一次利用双曲线分布来研究煤炭类期货的风险测度问题；并以对比概率密度曲线和样本Q-Q图的可视化方式证明了新假设的优越性；最后实际计算并比较了“左尾”和“右尾”各置信水平下的正态VaR、双曲线VaR和历史VaR以验证修正模型的风险度量精度的提升。

2 实证研究

2.1 数据来源与描述性统计

数据选取时间范围从2013年10月21日～2015年12月29日，数据以Wind商品品种指数中焦煤指数和动力煤指数作为样本,该品种基期为行业内第一个上市品种上市首日，基点为第一个交易日收盘后计算出的指数值。

指数公式见式(1)～(3)。

Wind商品品种指数=∑合约最新价×每个合约权重

(1)

每个合约权重=每个合约持仓额÷品种总持仓额

(2)

品种总持仓额=∑每个合约最新价×持仓量×交易单位，双边计算

(3)

获得样本期指数后以Rt=lnpt-lnpt-1计算收益率,pt为第t日指数值,pt-1为第t-1天的指数值,于是得到各包含539个样本的数据序列。对两Rt序列进行描述性统计结果见表1。

表1 样本数据描述性统计

对比可知，两样本的偏度和峰度与正态分布理论值差异较大。因此猜测其他种类分布能更好的拟合两序列。为证实此猜测，下文以K-S假设检验方法尝试找到最优拟合分布。

2.2 最优拟合分布的选择

2.2.1 K-S检验方法描述

K-S检验是以两位苏联数学家Kolmogorov和Smirnov的名字命名的一个拟合优度检验。K-S检验的基本思路是：先比较资料数据的理论累积频率分布与观测的经验累积频率分布，求出两者最大偏离值，然后在给定的显著性水平上检验这种偏离值是否是偶然出现的。

检验步骤如下所述。

1)提出假设。H0:Sn(x)=F0(x),H1:Sn(x)≠F0(x)。Sn(x)是随机样本观察值的累计概率分布函数，即经验分布函数，样本量为n；F0(x)是一个特定的累计概率分布函数，即理论分布函数。

2)计算统计量Dmax=max|Sn(x)-F0(x)|与相应p值。D=|Sn(x)-F0(x)|，如果对于每一个x值，Sn(x)和F0(x)都十分接近，则表明经验分布函数与理论分布函数的拟合程度很高，有理由认为样本数据来自服从该理论分布的总体。

3)比较p值与给定的显著性水平α。若p>α，则在α的显著性水平上，不能拒绝H0；否则，拒绝H1。

2.2.2 逐类排除错误分布

按照以上步骤进行正态性检验：无效假设(一般译为原假设)为“焦煤/动力煤指数收益率Rt服从正态分布”。通过计算得到焦煤样本的检验统计量=0.079 917,且p值为0.002 046，于是在1%的显著性下拒绝无效假设，接受了备择假设“焦煤指数收益率Rt不服从正态分布”；动力煤样本的检验统计量Ddlm=0.148 61，且p值为9.138×10-11，于是在1%的显著性下拒绝无效假设，接受了备择假设“动力煤指数收益率Rt不服从正态分布”。

为了排除不适用于描述煤炭类期货收益率分布的分布类型，以K-S检验方法检验焦煤与动力样本Rt是否服从beta, cauchy, chi-squared, exponential, f, gamma, geometric, log-normal,lognormal,logistic,negative binomial,normal,Poisson,t以及weibull分布。结果均显示在5%的显著性下应拒绝无效假设，即均不服从这些常用分布，因此尝试双曲线分布。

2.2.3 双曲线分布的K-S检验

以上各类分布的K-S检验在R软件中均有成熟的函数，因此可用来直接检验样本数据。但双曲线分布的K-S检验无成熟函数，因此需先假设焦煤和动力煤样本Rt服从双曲线分布，估计出分布参数，再进行K-S双样本检验。

一维的广义双曲分布(GH)具有如下形式的密度函数[14]，见式(4)～(6)。

(4)

(5)

(6)

式中：x∈R,μ∈R,Kλ(t)是λ阶的第三类修正贝塞尔函数，t>0。参数的取值范围为:如果λ>0，则δ≥0,|β|<α；如果λ=0，则δ>0,|β|<α；如果λ<0，则δ>0,|β|≤α。

GH分布的性质由参数向量θ=(λ,α,β,δ,μ)决定，α和δ决定密度函数的峰度，β决定偏度，μ和δ分别决定位置和尺度，λ决定尾部的厚度并标记不同的子类。改变λ可得不同尾部厚度的分布函数，衍生出不同尾部厚度的GH分布族的子类，λ=-0.5时为正态逆高斯分布，比如λ=1时为双曲线分布。双曲线分布的参数向量由θ=(π,ζ,δ,μ)表示。

分别生成两组服从以上双曲线分布的随机数据与样本数据进行K-S双样本检验。焦煤检验统计量Djm=0.051 9，p值为0.461 1；动力煤检验统计量Ddlm=0.027 8，p值为0.985 1。结果均显示在5%显著性下不能拒绝无效假设“煤炭类期货收益率服从双曲线分布”。

2.3 正态与双曲分布拟合度的可视化比较

为进一步证明双曲分布比正态分布更适于描述焦煤期货收益率,本文分别绘制了概率密度曲线对比图、正太分布Q-Q图、双曲线分布Q-Q图，见图1～3。

图2是焦煤期货指数正态分布Q-Q图,图3是双曲分布Q-Q图。图2、图3中斜线比较标准，斜率为1，如果散点与斜线重合度较高则样本数据分位点与理论分布分为点较为接近，即可证明样本服从该类型分布的可能性较高。图2散点曲线多次弯折，与斜线重合度不高，但图3散点曲线基本与直线重合，比较图2、图3可判定样本数据服从双曲分布的概率更高。

为进一步证明双曲分布比正态分布更适于描述动力煤期货收益率,本文绘制了概率密度曲线对比图、正太分布Q-Q图、双曲线分布Q-Q图，见图4～6。

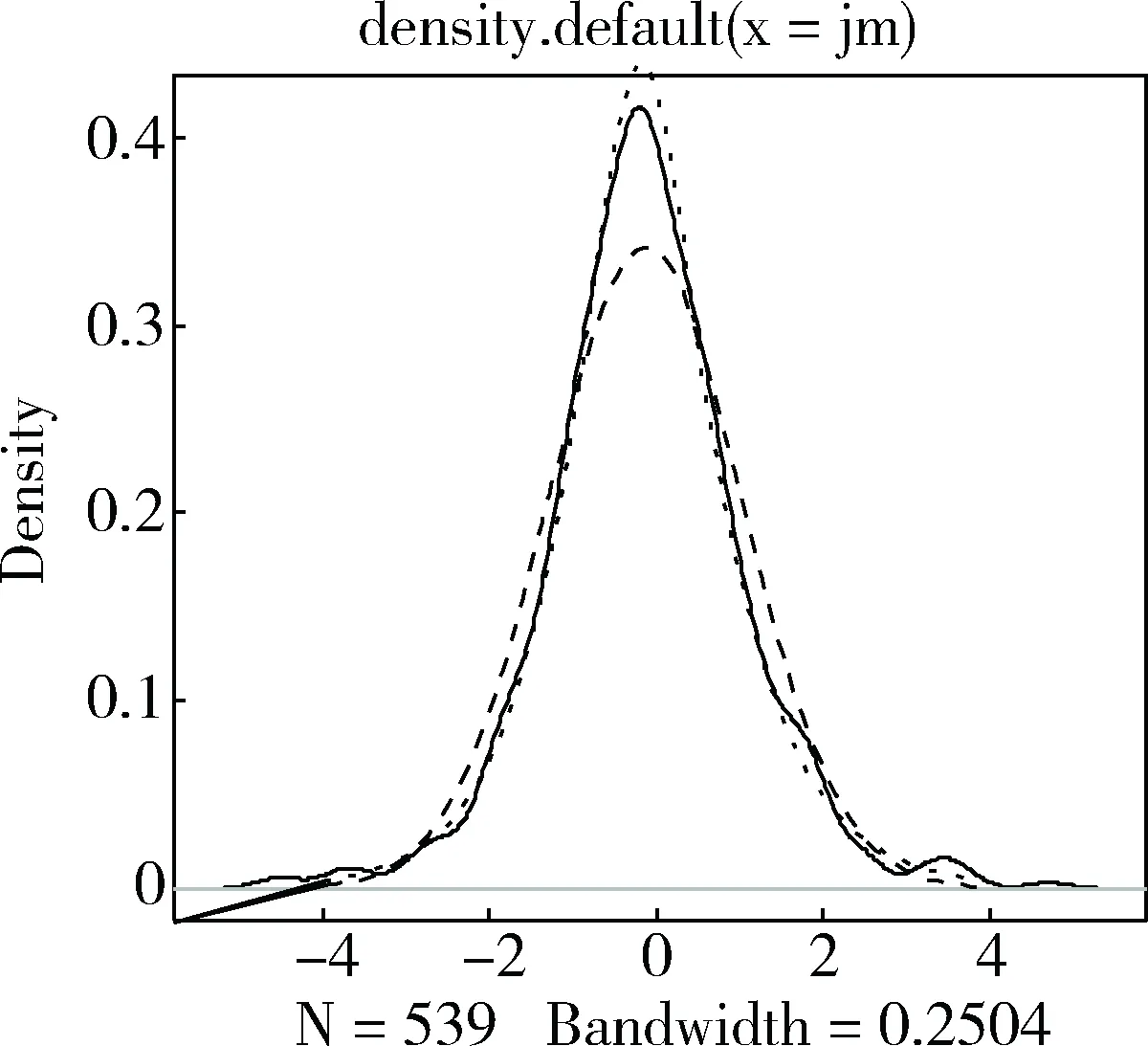
图1 焦煤样本、正态、双曲线概率密度曲线图

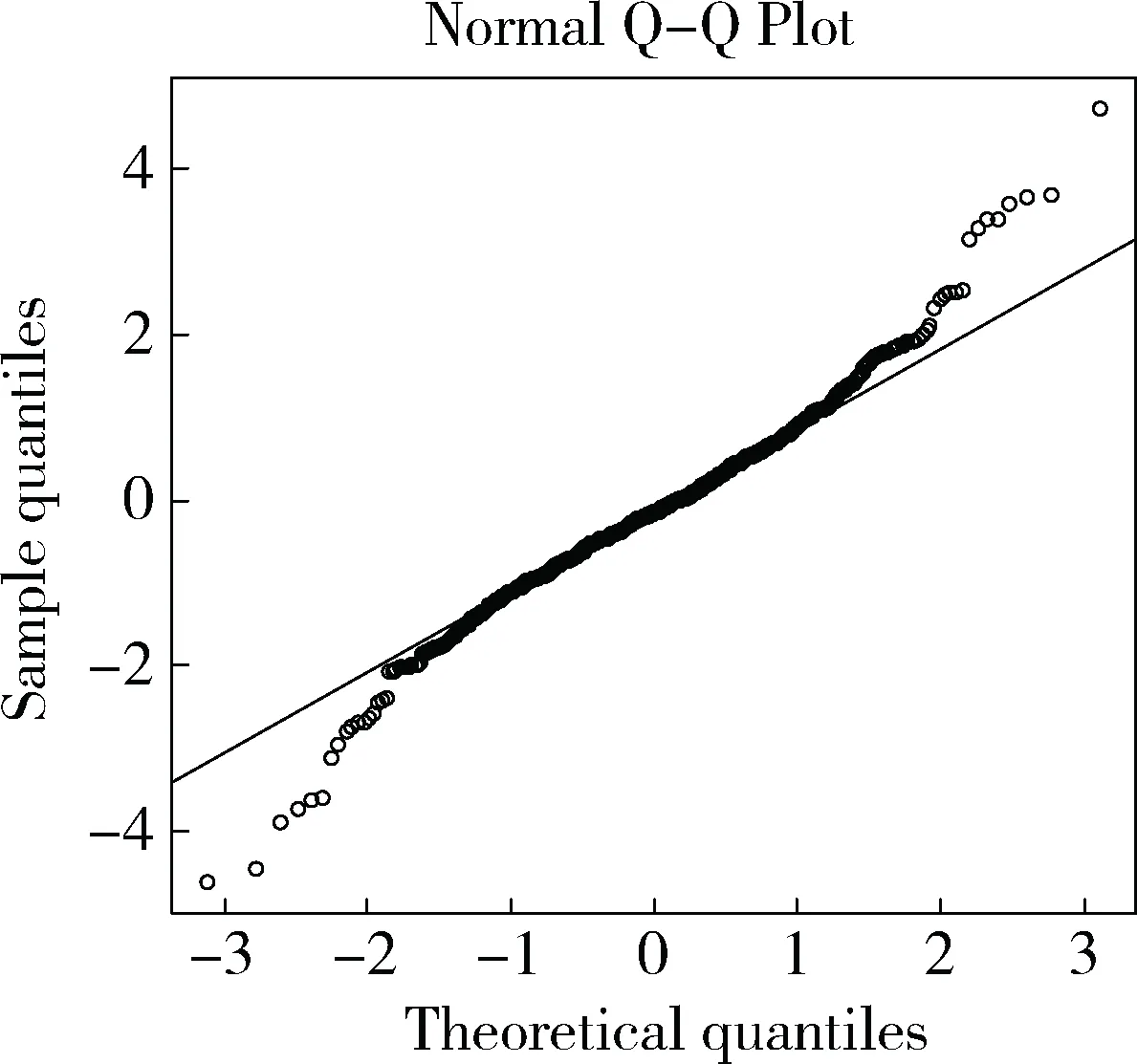
图2 焦煤正态Q-Q图

图3 焦煤双曲分布Q-Q图

图4 动力煤样本、正态、双曲线概率密度曲线图

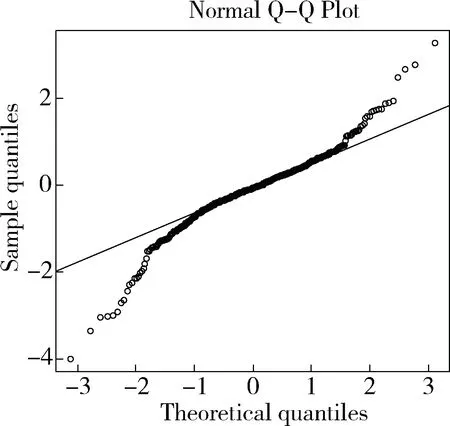
图5 动力煤正态Q-Q图

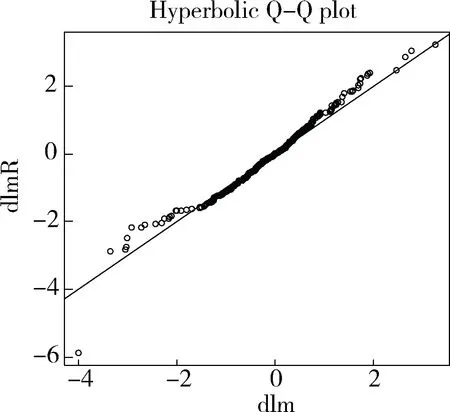
图6 动力煤双曲分布Q-Q图

图5、图6分别为动力煤正态分布与双曲线分布Q-Q图，图5、图6中斜线比较标准，斜率为1，如果散点与斜线重合度较高则样本数据分位点与理论分布分为点较为接近，即可证明样本服从该类型分布的可能性较高。图5散点曲线多次弯折，与斜线重合度不高，但图6散点曲线基本与直线重合，比较图5、图6，可判定样本数据服从双曲分布的概率更高。

3 VaR对比结果与结论

3.1 VaR方法描述

VaR是指面临“正常”的市场波动时“处于风险状态的价值”，即在给定的置信水平和一定的持有期限内，预期的最大损失量。通俗来讲就是一定可能性下某段时间损失的最大钱数。由此可知，要确定一个金融机构或资产组合的VaR值或建立VaR模型，必须首先确定以下三个参数：一是持有期间的长短；二是置信水平的大小；三是观察时点[15]。用公式表达，见式(4)。

VaRα=inf{l∈R:P(L>l)≤1-α}L=Vt-Vt-T

(4)

式中：T为持有期长度；a为置信水平;t为观察时点;L为损失;V为资产价值;l是使F(1)=a的数。

计算VaR通常用Risk Metrics模型。该方法假定资产组合的价值变化服从正态分布，即：L=(Vt-Vt-1)～N(μ,δ2)。VaR的计算公式为:VaR=P0×Zα。其中P0表示资产的初始市场价值，表示正态分布的分位数。本文以双曲线分布修正了正态分布假设，是对Za的修正。

此外，历史模拟法也常用于计算VaR。该方法以样本数据个数n与置信水平a的乘积取整得到序数N，取由小到大排列后的第N个样本数据，其值则为历史VaR。

3.2 结果与结论

参数确定后的双曲线分布不同显著性水平下的分位值与资产初值的乘积为VaR。取资产初值为100万元可得出不同显著性水平下的VaR值，在表2、表3中列示(期货可以做空，因此表2和表3列举了上下尾部对称的3对分位点)。

表2 100万元焦煤期货投资在不同置信度下VaR值(万元)的对比

比较不同方法所得VaR值，可以得到以下三点结论。

1)双曲分布VaR与历史VaR最为接近。此结果证明，把正态分布假设修正为双曲分布假设可以提高煤炭类期货价格风险度量的精度。

2)焦煤双曲线VaR与历史VaR间的差值小于动力煤双曲线VaR与历史VaR间的差值。此结果说明，双曲线法对焦煤期货指数VaR的估计更准。

3)各置信度下焦煤VaR均大于动力煤VaR。此结果说明，投资焦煤期货的风险高于动力煤期货。

[1] 李腊生，孙春花. 样本数据正态性转换时变VaR[J]. 统计研究，2012，29(5)：88-93.

[2] Mandelbrot B. The variation of certain speculative [J]. Journal of Bussiness, 1963, 36:394-419.

[3] Officer R. The distribution of stock returns[J]. Journal of the American Statistical Association, 1972, 67:807-812.

[4] Akgiray V, Booth G. The stable-law model of stock returns[J]. Journal of Business & Economic Statistics, 1988, 6: 51-57.

[5] 何建敏，朱林，常松. 中国股票市场价格波动的尺度特征[J]. 中国管理科学，2003，11(1)：1-5.

[6] Barndorff-Nielsen O. Exponentially decreasing distributions for the logarithm of partical size[J]. Proc Roy Soc London A, 1977, 353:401-419.

[7] Eberien E, Keller U. Hyperbolic distribution in finance[J]. Bernouli, 1995, 1:281-299.

[8] Barndorff-Nielsen O. Normal inverse gausssian distributions and stochastic volatility modeling[J]. Scandinavian Journal of Statictics, 1977,353:401-419.

[9] Prause K. Modeling Financial Data Using Generalized Hyperbolic Distribution[M]. FDM preprint 48. Freiburg: University of Freiburg, 1997.

[10] Barndorff-Nielsen O, Shepard N. Normal modified stable processes[J]. Theory of Probability and Mathematical Statistics, 2001, 65: 1-19.

[11] McNeil A, Frey R, Embrechts P. Quantitative Risk Management: Concepts, Techniques And Tools[M]. Princeton: Princeton University Press, 2005.

[12] 邹健. 广义双曲分布族及其在金融中的应用研究——参数估计、普通欧式期权定价和算法[J]. 系统工程学报，2001，16(3)：202-210.

[13] 郭海燕，李纲. 广义双曲线分布模型在我国证券市场风险度量中的应用研究[J]. 运筹与管理，2004，13(4)：106-109, 154.

[14] 刘昆仑,万建平,谷伟. 双曲分布在VaR模型中的应用[J]. 统计与决策，2007，232(4)：32-34.

[15] 李永民. 期货市场上的系统性风险和非系统性风险[J]. 金融与经济，2007，243(3)：45-48.

重大专项

编者按：

2013年9月，习近平总书记提出“一带一路”战略构想，描绘了具有划时代意义的全球战略新蓝图，为新形势下中国矿业全球化提供新的战略思路。“一带一路”地区能源及重要矿产资源极为丰富，与中国在矿业及相关领域互补性强，合作前景广阔。开展矿业与冶炼加工产业等领域产能合作是中国全面实施 “一带一路”战略最重要的组成部分，对促进各国经济社会发展、保障中国资源产业安全和国际运输通道安全均具有极为重要的意义。中国地质科学院矿产资源研究所陈其慎、于汶加研究团队以地质调查二级项目“‘一带一路’64国矿产资源供需格局及产能合作布局研究”项目为依托，系统开展了“一带一路”沿线国家经济社会发展、矿产资源分布及供需趋势、矿业及相关产业发展现状及趋势判断以及产能合作建议等方面的研究。本次专栏展示了研究团队对东南亚、伊朗、乌兹别克斯坦和波兰等几个典型国家的研究成果，以期为各类相关人员提供参考。

Distribution fitting and risk metrics of coal futures returns

LI Baiji, YANG Ziming, KONG Detai

(School of Management, China University of Mining and Technology (Beijing), Beijing 100083, China)

In recent years, the influence of falling coal prices makes coal futures’ price volatility risk increases. The market environment leads the VaR model which based on the normal distribution could not measure coal futures price risk accurately. Therefore, how to measure coal futures price risk accurately becomes a serious problem. This paper based on the VaR model, tries using K-S tests to find other distributions, which can improve the risk metrics accuracy, to replace the normal distribution assumptions. The K-S test results show that coal futures returns comply with the hyperbolic distribution; probability density curves and Q-Q figures show that the hyperbolic distribution fits the reture series better than the normal distribution; VaR calculation and comparison shows that the hyperbolic VaRs are closer to history VaRs than the normal VaRs, and coking coal futures’ VaRs are greater than power coal futures’ VaRs. Therefore, the VaR model based on the hyperbolic distribution is more suitable for coal futures investors to measure risk; investment risk of coking coal futures is bigger than that of power coal futures.

coal class futures; VaR; distribution fitting; normal distribution; hyperbolic distribution

2016-11-22

李百吉(1962-)，男，黑龙江大庆人，教授，博士生导师，研究方向为宏观经济、金融工程与风险管理、市场营销、能源经济管理，E-mail:13911056088@163.com；

杨子铭(1988-)，男，河北石家庄人，博士研究生，研究方向为能源金融，E-mail: 2282375429@qq.com;

孔德泰(1985-)，男，河北衡水人，博士研究生，研究方向为创新管理。

F223

A

1004-4051(2017)03-0043-05