水下载体SINS/USBL组合导航滤波方法研究

于 浩，王彦国，胡小毛，王桂如

(天津航海仪器研究所，天津 300131)

水下载体SINS/USBL组合导航滤波方法研究

于 浩，王彦国，胡小毛，王桂如

(天津航海仪器研究所，天津 300131)

捷联惯性导航系统(SINS)具有短期定位精度高的优点，但其定位误差随时间发散，超短基线(USBL)在其有效工作范围内定位误差不发散，且由于受作用距离及复杂水下环境的影响,其定位数据不连续，离散度大，野值多。水下载体导航采用SINS/USBL组合导航，可充分发挥各自的优势。根据USBL量测信息的特性，给出了一种基于改进的带观测噪声时变估计器的Sage-Husa自适应Kalman滤波方案，经实物数据仿真验证了此滤波方案的有效性。

SINS;USBL;组合导航;Sage-Husa自适应滤波

0 引言

近年来在全世界范围内，水下运载体(AUV、ROV)在环境监测和监督，河口、海港和管线的水下检查，地质和生物勘察等方面的应用越来越广泛。这些应用场合均要求使用低成本、紧凑、高性能的导航系统，能够精确测量运载体的位置和姿态[1-2]。

SINS具有体积小、质量小、可靠性高的优点，随着SINS成本的不断降低，越来越多地装备到了各类AUV和ROV中，用以替代原来的低精度罗经，为水下载体提供全天候、完全自主、不受外界干扰的全导航参数。SINS具有优异的短期精度，但其误差会随时间发散，通常使用其他量测信息来辅助SINS，构成组合导航系统，抑制误差发散。最典型的就是SINS/GNSS组合导航系统，但GNSS信号无法到达水下，为了获取GNSS校正信息需要水下载体定期上浮，消耗了过多的时间、动力及成本。使用声学定位技术辅助，例如长基线(LBL)系统，需要繁琐而耗时的布放、校准及回收；使用安装于船体的短基线(SBL)系统，必须将其紧密安装在船身并且受到船体自然弯曲的影响；使用超短基线(USBL)系统，具有适宜的精度，且使用方便，成为辅助SINS构成组合导航系统的理想选择[3-4]。

USBL提供的绝对位置是经视在位置坐标变换而来，这样导致SINS/USBL组合导航系统的量测信息误差特性叠加了USBL自身的声速误差、时延误差、测相误差以及航姿误差等[5]，不再满足传统Kalman滤波量测噪声为零均值高斯白噪声的假设条件。文献[6]将USBL误差建模为有色噪声和白噪声的和，并考虑到了水声数据延迟特性的影响,提出了几种解决方案，但并没有给出具体的组合滤波算法[6]。本文通过对SINS/USBL组合量测信息误差特性分析，使用了观测噪声时变估计器对其量测噪声方差进行实时估计，通过实物数据仿真验证了算法的正确性。

1 系统组成与工作原理

组合导航系统的组成如图1所示。SINS中安装有3个陀螺和3个加速度计，并运行捷联解算程序。USBL采用传统的测距及测相原理对目标进行定位，位置固定的应答器提前标定好，并由USBL实时测量其与USBL基阵间的时延及相位差信息，经过位置变换获得USBL基阵处的绝对位置。SINS利用自身解算位置与USBL位置之差作为观测量进行Kalman滤波，补偿SINS随时间增长的定位、速度、姿态等误差。

图1 系统组成原理图Fig.1 Diagram of system construction

2 USBL位置变换算法及定位误差模型

2.1 USBL视在位置到绝对位置变换算法

基阵坐标系定义为：坐标原点位于阵元中心，横轴X，纵轴Y且与垂向轴Z构成右手坐标系。载体系定义为：坐标原点位于载体摇摆中心，X轴直线右舷，Y轴指向舰艏，Z轴与X、Y轴垂直且构成右手坐标系。导航坐标系为东北天地理坐标系。

USBL直接测量得到的是信标与基阵之间的相对位置信息，将此相对位置(视在位置)变换为基阵处的绝对位置需要经过相应的变换。设已标定完成的应答器位置为Pte，USBL测量得到的应答器在基阵坐标系中的相对位置为Pta，基阵的位置为Pae，则[7]

Pae=Pte+CanPta

(1)

式中,Can为基阵坐标系向地理坐标系转换的方向余弦矩阵，由载体的航向角、横摇角和纵摇角构成。

2.2USBL定位误差模型

使用ΔPta=[σaxσay]表示USBL测量得到的相对基阵系x和y方向的定位误差为

ΔPta=[σaxσay]=R[δaxδay]

(2)

其中，R为USBL基阵与被测目标间的斜距。忽略阵元间距误差的影响，则超短基线定位系统的声学相关的定位误差定义如下[8]：

(3)

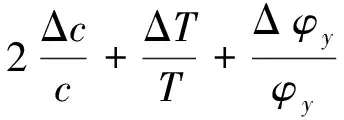
(4)

α为目标与基阵系x轴的夹角，β为目标与基阵系y轴的夹角，c为水中声速，Δc为声速误差，T为时延，ΔT为时延测量误差，φx、φy为对应轴接收到目标信号的相位差，Δφx、Δφy为对应轴相位差的测量误差。

由式(2)、式(3)、式(4)可以看出，USBL声学定位精度与斜距、目标与基阵系坐标轴夹角、时延及相位测量精度相关。

2.3USBL绝对定位误差模型

对式(1)求全微分，得基阵的位置误差为

ΔPae=ΔPte+ΔCanPta+CanΔPta

(5)

其中，ΔPae为基阵的位置误差，ΔPte为应答器的标定位置误差，ΔCan为姿态阵误差，ΔPta为USBL声学定位误差，由式(2)、式(3)、式(4)确定。

3 SINS/USBL组合滤波模型及仿真

3.1 量测噪声特性分析

采用高精度的位置基准(例如RTKGNSS)和标定算法，可将信标的标定误差控制在亚米级，故可将式(5)中的ΔPte项忽略不计，则量测噪声变为

ΔPae=ΔCanPta+CanΔPta

(6)

由式(6)可以看出，使用USBL变换后的位置作为观测信息时，观测误差与姿态角误差、基阵与信标间的相对位置及声学定位误差有关。

假定信标深度为50m，USBL定位数据频率为1Hz。SINS陀螺漂移为0.01(°)/h，加速度计零偏为5×10-5g，声速相对常值误差为0.001c(c为声速真实值)，测时常值误差为0.0005s，测相常值相对误差为1%，随机误差方差与常值误差相同。载体在距离信标垂直距离为50m的水平面上运动，分两种情况对USBL水声定位误差进行仿真，一是载体绕信标环形，半径为100m；二是载体沿通过信标在水平面投影点的直线航行，载体起点在信标的投影正上方，速度为2kn。仿真结果如图2、图3所示。

图2 载体环形USBL绝对定位误差Fig.2 USBL absolute positioning error in ring motion

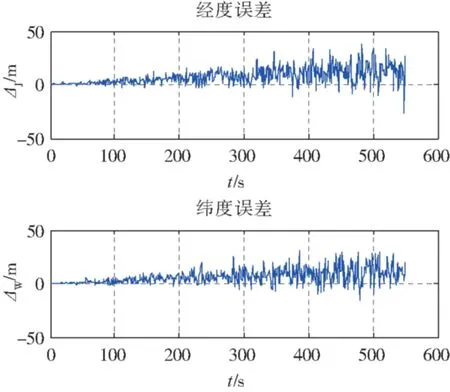
图3 载体直线航行USBL绝对定位误差Fig.3 USBL absolute positioning error in straight line

未完全补偿的声速误差、时延误差及测向误差等系统常值误差的存在，使得USBL定位误差呈现非零均值特性。由图2、图3可以看出，当载体绕信标环形时，因USBL测量的斜距R与2个相位角α、β均为常值，故其定位误差会载体航向不同呈被正弦曲线调制的噪声形式；当载体直航时，由于斜距及2个相位角均发生改变，定位误差随斜距的增加误差不断增大。两种航迹的误差均具有非平稳噪声特性。

3.2 滤波模型

采用东北天坐标系作为导航坐标系，取INS的2个水平位置误差、2个水平速度误差、3个姿态角误差、3个加速度计零偏、3个陀螺仪常值漂移作为状态变量，并将INS解算位置与USBL量测位置之差作为观测变量，系统模型为[9]：

(7)

其中，F为系统矩阵，H为量测矩阵，W为系统过程噪声，包括3个加速度计零偏、3个陀螺仪常值漂移，W～(0,Q)，V为量测噪声。

观测量Zk=Pins-Pae=ΔPins-ΔPae，Pins为惯导解算水平位置,ΔPins为惯导解算位置误差。可见量测噪声Vk的特性完全取决于USBL的绝对定位误差。

3.3 滤波算法

根据3.1节的分析可知，采用USBL量测位置作为观测量时，观测噪声具有时变的均值和方差，传统的Kalman滤波方法在量测噪声不满足高斯白噪声的条件时无法获得最优解，甚至会引起滤波器的发散。Sage-Husa自适应Kalman滤波方法具有原理简单、实时性好，以及可同时估计出过程噪声和观测噪声一、二阶矩等特点，但直接使用该算法估计过程噪声和观测噪声很容易引起滤波发散，同时算法对初值敏感及噪声统计特性估计有偏[10]。考虑到系统过程噪声较为稳定且方差误差较小，采用改进的Sage-Husa自适应滤波算法，只对观测噪声的统计特性进行估计，会提高算法的实用性。

带观测噪声时变估计器的简化Sage-Husa自适应滤波算法如下：

(8)

(9)

(10)

(11)

(12)

Rk= (1-dk)Rk-1+

(13)

dk=(1-b)/(1-bk+1)

(14)

其中,b为遗忘因子，0

3.4 仿真验证

根据以上的模型及滤波算法，针对3.1节的仿真数据进行仿真计算，仿真结果如图4、图5所示。

图4 载体环线航行滤波误差对比Fig.4 Comparison of filtering error in ring motion

图5 载体直线航行滤波误差对比Fig.5 Comparison of filtering error in straight line

最终的仿真结果对比如表1所示。

表1 仿真结果对比

3.5 实验验证

试验区域选择千岛湖相对宽阔的水域，东西向及南北向长度均为2.5km以上，水深在50m左右。位置基准采用RTK DGPS，精度优于0.1m。试验选用的惯性设备其标度因数重复性、稳定性，标度因数非线性度及不对称度均为5×10-6，零偏稳定性和重复性均优于0.01(°)/h。USBL定位系统由基阵、甲板单元及对应的应答器组成，定位精度为1m±1%D(D为基阵与应答器之间的距离)。

试验过程中首先进行应答器的布放及标定，使用反转长基线方法标定应答器的位置，同时计算IMU与USBL之间的安装误差角并补偿进系统。惯导对准完成后进入USBL作用距离范围内，收到USBL提供的原始定位信息(与应答器之间的斜距、基阵坐标系下应答器的横纵距离)反向解算出基阵的位置，在补偿基阵与IMU之间的杆臂误差后进行位置组合，输出组合后的导航信息。

采用标准Kalman滤波和带观测噪声时变估计器的简化Sage-Husa自适应滤波仿真结果如图6所示。

图6 不同组合滤波算法轨迹比对Fig.6 Trajectory comparison of different combination filtering algorithms

图6的细节图显示了两种不同方案的效果，载体机动过程中，相对于普通Kalman滤波方案来说，自适应滤波方案能很好地跟踪GPS真实轨迹。

表2给出了普通Kalman滤波组合算法和自适应Kalman滤波组合算法的实验比对结果，从系统定位误差来看，自适应Kalman滤波组合方案下系统定位误差要优于普通Kalman滤波组合方案。

表2 不同组合滤波算法结果对比

4 结论

本文采用SINS/USBL组合导航方案，根据USBL量测信息的特性，给出了一种基于改进的带观测噪声时变估计器的Sage-Husa自适应Kalman滤波方案，经实物数据仿真结果表明自适应Kalman滤波方案相比常规Kalman滤波器更能适应USBL有色噪声的特性。

[1] 佟盛. AUV导航系统及技术发展[C]. 中国造船工程学会2006年船舶通讯导航学术会议, 2006: 241-244.

[2] 李俊,徐德民,宋保维,等. 自主式水下潜器导航技术发展现状与展望[J]. 中国造船,2004, 45(3): 70-77.

[3] Bingham B. Navigating autonomous underwater vehicles[D]. U. S. A Franklin W. Olin College of Engineering,2008.

[4] 钱洪宝,孙大军. 水声定位系统现状[J]. 声学技术,2011, 30(3): 389-391.

[5] 喻敏. 长程超短基线定位系统研制[D]. 哈尔滨： 哈尔滨工程大学, 2006： 19-24.

[6] Mandt M, Gade K, Jalving B. Integrating DGPS-USBL position measurements with inertial navigation in the HUGIN 3000 AUV[C]//Proceedings of the 8thSaint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg, Russia, 2001: 28-30.

[7] Arkhipov M. A coordinate determination algorithm for USBL systems[C]//Proceedings of the 2thWSEAS International Conference on Circuits, Systems, Signal and Telecommunications. Acapulco, Mexico, 2008: 50-55.

[8] 田坦. 水下定位与导航技术[M]. 北京: 国防工业出版社, 2007: 27-44.

[9] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006: 355-361.

[10] 付梦印,邓志红，闫莉萍. Kalman滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 2010: 108-118.

Research on SINS/USBL Integrated Navigation Filitering Method for Underwater Vehicles

YU Hao,WANG Yan-guo, HU Xiao-mao, WANG Gui-ru

(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

Strapdown inertial navigation system (SINS) has the advantage of short-term high precision, butitspositioning error diverges over time. The positioningerror of ultra short baseline(USBL) doesn’t diverge within its effective working range, but itspositioning databecomes discontinuity with greater discreteness and more outliersdue to theimpact of operating range and complicated underwater environment. While SINS/UBSL integrated navigation scheme can help underwater vehiclemake full use of respective advantages.According to the characteristic of the USBL measurement information, a Sage-Husa adaptive Kalman filtering scheme which is based on improved observation time-varying noise estimatoris presented. Simulation verify the effectiveness of filtering scheme.

SINS; USBL; Integrated navigation; Adaptive filtering based on Sage-Husa

10.19306/j.cnki.2095-8110.2017.01.004

2016-10-11；

2016-11-10。

装备预研船舶重工联合基金(6141B04050301-04)

于浩(1964-)，男，研究员，主要从事导航制导与控制方面的研究。E-mail：yuhao_707@123.com

U666.12

A

2095-8110(2017)01-0020-05