基于半角机构的反射镜光电平台测角研究

江燕俊，丁海山，陈宝国,2



基于半角机构的反射镜光电平台测角研究

江燕俊1，丁海山1，陈宝国1,2

（1. 中航工业空空导弹研究院，河南 洛阳 471009；2. 航空制导武器航空科技重点实验室，河南 洛阳 471009）

偏仰两轴反射镜光电平台通过控制光路中反射镜的转动实现视线的角位置跟踪。实时测量视线和视轴的角误差是完成角位置跟踪的前提。传统的光电稳定平台将探测成像系统安装在稳定平台上，所以目标像在图像平面中的脱靶量等于视线角误差。反射镜光电平台采用探测成像系统和平台分离的结构形式且光路发生折转，使得目标脱靶量不再等于视线角误差。基于光学反射定律和等距坐标变换，对反射镜光电平台的视线角误差计算进行了研究，得到目标脱靶量和视线角误差的映射关系，并且可以将其近似为关于外框架角的旋转变换。通过数值仿真和样机实验验证了分析结果的正确性。

反射镜光电平台；半角机构；目标脱靶量；视线角误差

0 引言

光电稳定平台可以隔离基座的运动，保持负载姿态相对惯性空间稳定，在飞机、舰艇、车辆、导弹、卫星等许多领域得到了广泛的应用[1]。利用稳定平台可以实现目标的捕获、跟踪与瞄准等功能。

传统的偏仰两轴光电平台采用内外框架转轴正交设计，稳定平台与俯仰框架固连[2-3]。目标的红外辐射沿光路汇聚于探测器焦平面上。由于探测器和光学系统作为负载安装在光电平台上，因此可以直接测量出弹目视线相对于平台的角位置偏差，即目标像在图像平面中的脱靶量[4]。传统光电平台的结构体积和转动惯量一般较大，需要通过框架的优化设计来实现较小的转动惯量，以便满足系统的技术指标[5]。由于结构上刚度强度的约束，这种优化设计的效果具有局限性。

随着光学成像跟踪技术的发展，光电稳定平台系统已朝着小型化、轻量化和集成化发展。为满足结构小型化和响应快速的要求，近年来将库德光路[6-7]和两轴稳定平台组合使用的反射镜光电平台得到广泛关注[8-9]。文献[8]深入分析了各种常见反射镜平台的视轴运动学关系和视轴稳定控制技术。由于光束经过库德光路转折后能够随轴系旋转，再加上探测器焦平面固连于弹体上的原因，目标脱靶量已不再直接对应弹目视线与平台的空间角位置。文献[10]研究了一种包含4块平面镜的反射镜平台的物像变换关系，推导出了明确的物像坐标变换公式，该公式实际上就是目标脱靶量和视线角位置误差的映射关系。本文研究的基于半角机构的反射镜光电平台采用库德光路折转传递设计，利用半角机构驱动反射镜来控制光轴指向，使目标稳定成像于探测器焦平面，从而得到目标像在图像平面中的脱靶量。基于光学反射定律和等距坐标变换研究反射镜光电平台对视线角位置误差测量，得到目标脱靶量和视线角位置误差的映射关系。利用三角函数小角度近似，将其近似为关于外框角的旋转变换。通过数值仿真和样机对目标的跟踪实验验证了分析结果的正确性。

1 平台结构及坐标系定义

1.1 平台结构

偏仰两轴反射镜光电平台结构示意图如图1所示。红外探测器弹体固连，光学系统采用库德光路。光学系统中的反射镜1安装在平台上，用于控制光轴指向。平台采用偏航框架内套俯仰框架的结构形式，通过半角机构控制反射镜1做俯仰和偏航运动，实现将目标实时、稳定、清晰地成像于探测器焦平面上。

图1 反射镜光电平台结构示意图

1.2 坐标系定义

反射镜光电平台相关坐标系的定义如下：

弹体坐标系b-bbb：原点位于弹体质心。bb轴沿弹体纵向轴线，指向导弹头部为正；bbb平面位于弹体纵向平面内，bb轴向上为正；bb轴符合右手坐标系定义。

外环坐标系o-ooo：原点位于位标器回转中心。oo轴与偏航框架转轴固连，向上为正；oo轴与oo轴垂直，初始位置与弹体纵轴重合，向前为正；oo轴符合右手坐标系定义。

内环坐标系p-ppp：原点位于位标器回转中心。pp轴与俯仰框架转轴固连，向右为正；pp轴与pp轴垂直，初始位置与弹体纵轴重合，向前为正；pp轴符合右手坐标系定义。

镜面坐标系11-111：原点和内框架坐标系的原点重合。11轴和内框架坐标系pp轴在镜面上的投影平行；11轴垂直于11轴且和镜面成45°角；11轴垂直于111平面，且符合右手坐标系定义。内框架坐标系处于零位时，镜面坐标系1和内框架坐标系重合。

镜像坐标系111-111111：镜像坐标系1是镜面坐标系1关于平面镜1所成的像。

镜面坐标系22-222：原点位于弹轴与平面镜2的交汇处。镜面坐标系2和弹体坐标系平行。

镜像坐标系222-222222：镜像坐标系2是镜面坐标系2关于平面镜2所成的像。

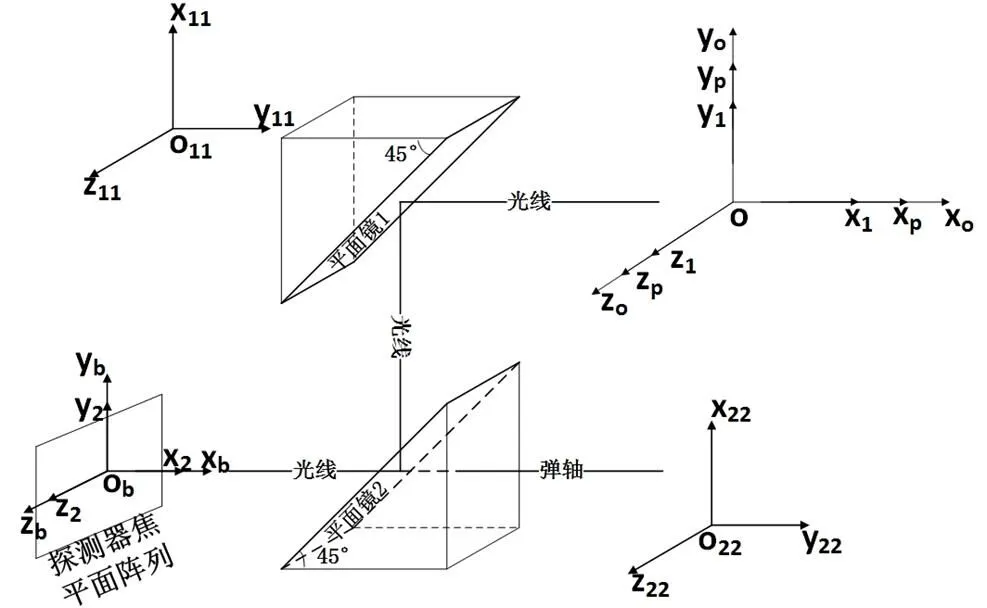
图2 各坐标系的空间位置关系

图3 各坐标系的转换关系

2 目标测角分析

2.1 半角机构的转角变换

光学成像系统中的平面反射镜1利用半角机构固连于内框架上。当俯仰框架运动时，平面反射镜镜1与内框架保持1/2倍角关系做俯仰运动。根据坐标变换，镜面系1与内环系之间保持式(1)的变换关系：

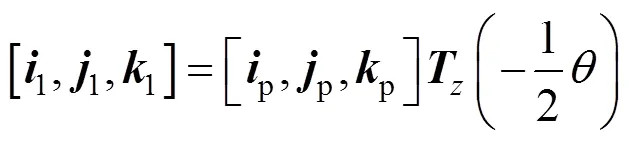
2.2 测角传递

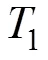
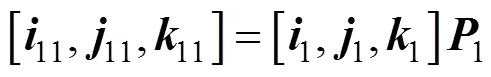
同理，镜面坐标系2与镜像坐标系2之间关系如式(3)所示：

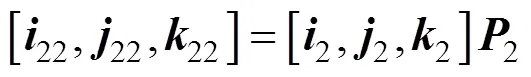
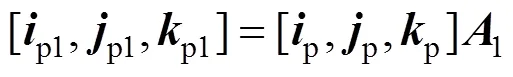
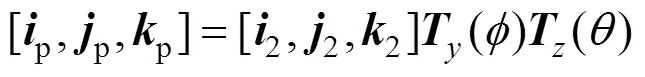
带入式(4)有：

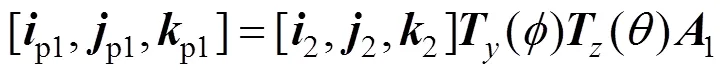
根据式(3)、(4)、(5)，基矢p1、p1、p1在平面反射镜2上所成的像为：

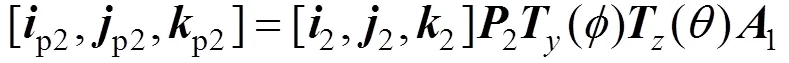
式(6)结合镜面坐标系1与镜面坐标系2的转换关系：

可以得到：

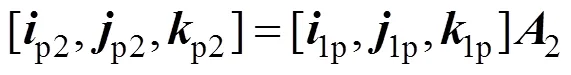
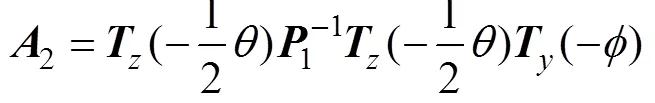
因此，根据式(4)和(7)可以得到内框架矢量经过平面反射镜1和2后的变换关系为：

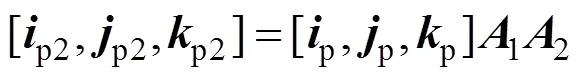
反射镜光电平台上的平面反射镜1、2组合形成独特的光学滑环结构，这种光学滑环所成的像可视为两个等距变换的合成，即＝12。

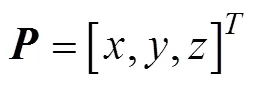
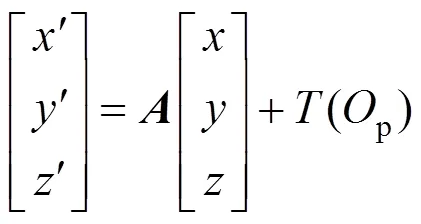
式中：(p)是原点p的像在内环系中的坐标。

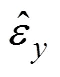
视线p上的单位矢量，其在内环系中的方位角为，高低角为，故在内环系中：

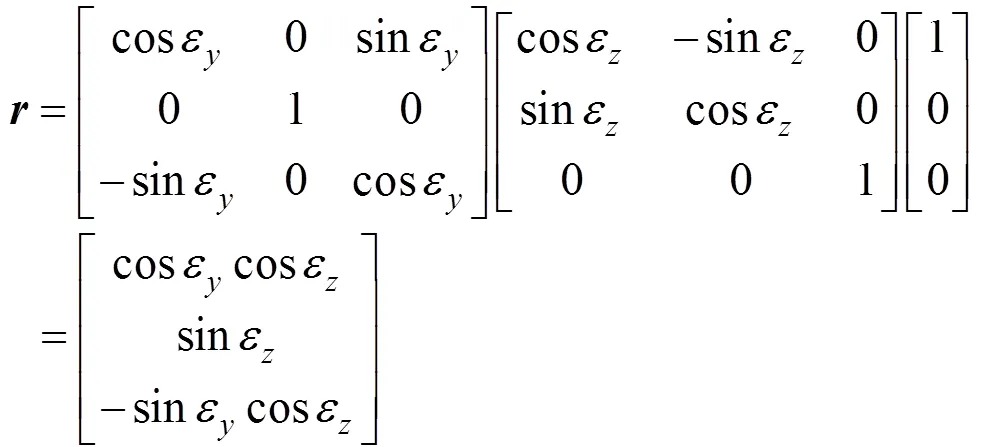
在光学滑环作用下，视线单位矢量的像¢在内框架坐标系下的投影为：¢＝。

同时，¢在弹体坐标系下的投影为：

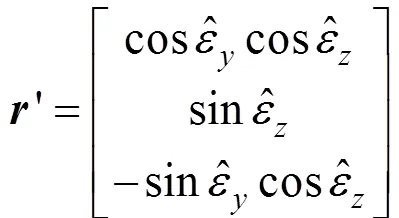
根据弹体坐标系到内框架坐标系的坐标变换关系，可以得到视线相对平台的角误差为：

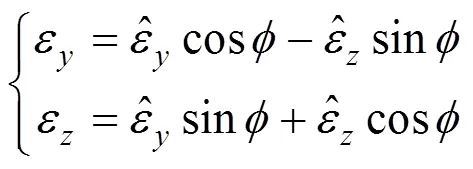
公式(11)的对应关系可逆，同样可以得到目标脱靶量的表达式：

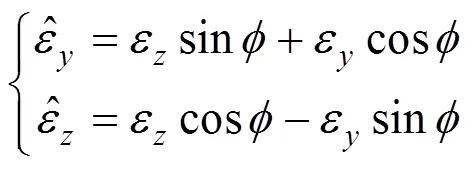
3 仿真和实验

式(10)给出了目标脱靶量和视线相对平台角误差的映射关系。这里通过构建视线相对弹体的运动模型，对近似公式的精度进行的仿真分析和样机实验验证，以评估其工程应用的可行性。

构建光电平台的运动模型如下：

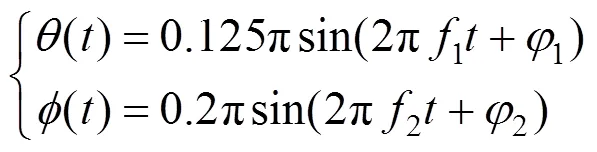
式中：1＝2，2＝1.5；1＝0.0175，2＝0.0349。

视线相对平台的运动模型如下：

式中：wx＝80，Ay＝－0.8，Az＝26；Yx0＝60，Yy0＝－0.6，Yz0＝0，fy＝fz＝0.5；采样时间0.001s，仿真时长1s，结果见图4和图5。图4中(a)和(b)为视线相对平台在方位和高低方向上的角误差；(c)和(d)为偏航、俯仰框架角。图5给出了其近似公式(12)解算的目标脱靶量及近似误差，其中(a)和(b)为目标在俯仰和方位方向上的脱靶量，(c)为探测器焦平面上目标的运动轨迹，(d)和(e)为采用近似公式(12)产生的计算误差量。从仿真结果可以看出近似误差不大于0.002个像素。

在某型实验样机中，利用视线角误差近似公式(12)进行目标跟踪实验，光电平台实现了对目标的稳定跟踪。输出其中一段时间内的数据进行分析，结果如图6和图7所示。实验结果表明，样机在动态跟踪机动目标的过程中，视线角误差公式(12)的近似误差不大于0.0004个像素，远满足于工程应用对误差不大于0.1个像素的要求。

图5 目标脱靶量及近似误差

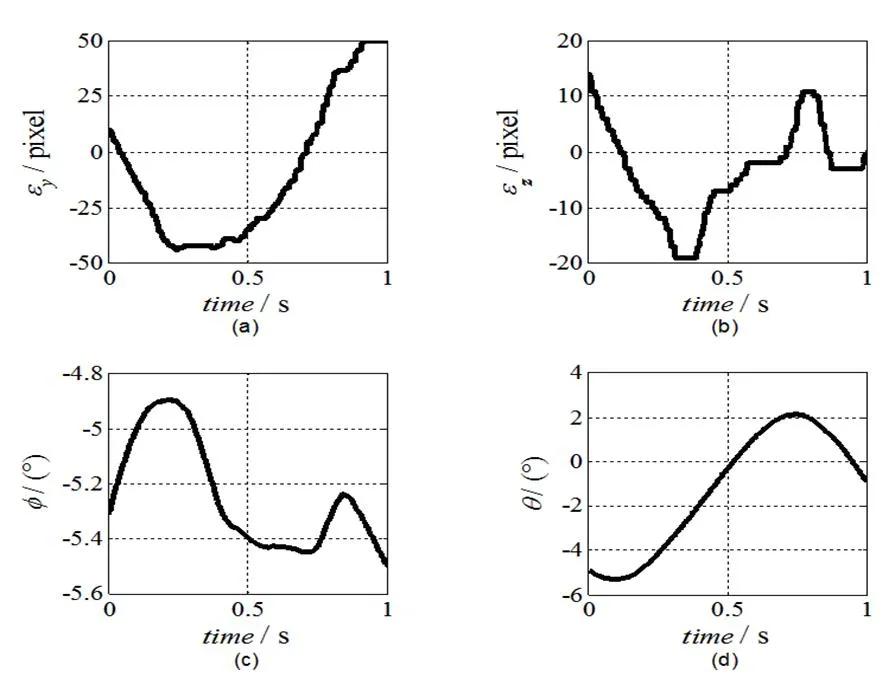
图6 样机实验中视线相对平台的角误差及框架的运动

图7 样机实验中目标脱靶量及近似误差

4 结论

本文研究了基于半角机构的反射镜光电平台对弹目视线角位置的测量，分析了视线相对平台的角位置误差计算。基于光学反射定律和等距变换原理，得出了目标脱靶量和视线相对平台角位置误差的映射关系，利用三角函数小角度近似，该影射关系可以近似为关于外框架角的旋转变换。数值仿真验证了分析结果的正确性。最后利用近似公式计算得到视线角误差作为跟踪回路的输入，通过样机对目标的跟踪实验表明近似公式满足工程应用的要求。

[1] 刘廷霞, 王伟国, 陈健. 车载惯性平台稳定位置解算算法[J]. 中国光学, 2012, 5(5): 537-543

LIU Tingxia, WANG Weiguo, CHEN Jian. Position arithmetic for a vehicular inertial stabilized platform[J]., 2012, 5(5): 537-543.

[2] 李红光, 纪明, 吴玉敬, 等. 大俯仰角度的两轴两框架平台稳定技术[J]. 应用光学, 2015, 36(6): 823-828.

LI Hongguang, GI Ming, WU Yujing, et al. Stabilization technology for two-axis two-framework platform with big pitching angle[J]., 2015, 36(6): 823-828.

[3] 张玉良, 耿天文, 刘永凯. 动基座光电平台视轴自稳定控制系统设计[J]. 国外电子测量技术, 2015, 34(9): 38-42.

ZHANG Yuliang, GENG Tianwen, Optical axis self-stablization control system’s design for moving base optical-electrical stable[J]., 2015, 34(9): 38-42.

[4] 花文涛, 丁海山, 贾晓洪, 等. 成像导引头光轴与视线之间相对运动的研究[J]. 红外技术, 2014, 36(1): 31-36.

HUA Wentao, DING Haishan, JIA Xiaohong, et al. Relative movement between line of sight and light axis of imaging seeker[J]., 2014, 36(1): 31-36.

[5] 刘长顺, 王兵, 陈兆兵. 车载光电稳定平台外框架优化设计[J]. 中国光学, 2011, 4(6): 606-610.

LIU Changshun, WANG Bing, CHEN Zhaobing. Optimization design of external border for vehicle opto-electronic stabilized platform[J]., 2011, 4(6): 606-610.

[6] 乔健, 高云国, 韩光宇, 等. 水平式两轴转台中库德光路的快速装调[J]. 光学精密工程, 2010, 18(8): 1760-1765.

QIAO Jian, GAO Yunguo, HAN Guangyu, et al. Fast alignment of Coude optical system in alt-alt two axis tracking turntable[J]., 2010, 18(8): 1760-1765.

[7] 魏群, 艾兴乔, 贾宏光. 小型可见光双视场光学系统的研制[J]. 光学精密工程, 2012, 20(4): 739-744.

WEI Qun, AI Xingqiao, JIA Hongguang. Development of small-scale and dual-field visible and dual-field visible light optical system[J]., 2012, 20(4): 739-744.

[8] 宋江鹏, 孙广利, 周荻, 等. 反射镜光电平台视轴稳定技术研究[J]. 红外与激光工程, 2015, 44(6): 1904-1911.

SONG Jiangpeng, SUN Guangli, ZHOU Di, et al. Line-of-sight stabilization techniques for mirror electro-optical platform[J]., 2015, 44(6): 1904-1911.

[9] 宋江鹏, 孙广利, 周荻, 等. 偏轴反射镜平台视轴稳定技术及建模分析[J]. 红外与激光工程, 2015, 44(8): 2484-2490.

SONG Jiangpeng, SUN Guangli, ZHOU Di, et al. Line-of-sight stabilization and modeling analysis of bias shafting mirror platform[J]., 2015, 44(8): 2484-2490.

[10] 尚超, 王军平, 吴军彪. 滚仰式光滑环物象变换关系仿真研究[J]. 红外与激光工程, 2011, 40(9): 1768-1773.

SHANG Chao, WANG Junping, WU Junbiao. Simulation of object-image transformation for roll-pitch seeker with slick chain[J]., 2011, 40(9): 1768-1773.

Measurement for Target Angular Error of Mirror Electro-optical Platform Based on Half-angular Mechanism

JIANG Yanjun1，DING Haishan1，CHEN Baoguo1,2

（1. AVIC China Airborne Missile Academy, Luoyang 471009, China; 2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471009, China）

Yaw-pitch two axis mirror electro-optical platform is able to trace angular position of line-of-sight by controlling the rotation of the mirror setting in the optical path. Real-time measurement of the angular error between the line-of-sight and the optical axis is the prerequisite for tracing angular position. Because imaging system is set on the traditional photoelectric stabilized platforms, target undershoot error in the image is equal to the angular error of line-of-sight. Mirror electro-optical platform uses the structure of separation between the imaging system and the platform and reflective optical paths, therefore target undershoot error is not equal to the angular error of line-of-sight any more. Based on the law of reflection and equidistant alternation theory, calculations for angular error of line-of-sight are studied. The mapping relation between the target undershoot error and angular error of line-of-sight is obtained. And the mapping is able to approximate the rotation transformation about the angle of outer frame. The correctness of analysis results is tested by numerical simulations and the prototype experiment.

mirror electro-optical platform，half-angular mechanism，target undershoot error，angular error of line-of-sight

TJ765.4

A

1001-8891(2017)04-0299-05

2016-06-15；

2016-08-09.

江燕俊（1979-），男，工程师，硕士，主要研究领域红外导引头伺服控制技术。E-mail：284593583@qq.com。