双向竖井贯流泵装置数值模拟及试验分析

夏 烨，汤方平，石丽建，谢传流，张文鹏

(扬州大学水利与能源动力工程学院，江苏 扬州 225009)

0 引 言

竖井贯流泵作为一种新型的低扬程泵站形式，发展迅速，广泛应用于南水北调东线的低扬程双向大型泵站中[1]。竖井贯流泵装置将电机、齿轮箱安装于竖井中，具有结构简单，进、出水流道顺直，泵站装置效率高，工程土建投资较少及便于管理维护的优点[2,3]。

陈荣新等[4]对泵站装置模型进行指定的叶片角度的能量试验及汽蚀特性试验，比较正反向效率得出流道设计时要减小竖井宽度，适当加大轴长度的观点；陈会向等[5]对模型泵不同的转轮叶片、叶轮位置及导叶位置方案进行了数值模拟，确定了改造泵装置模型结构参数，并分析了改进模型的综合特性及流场分布规律；刘君等[6]比较研究了前、后置竖井贯流泵装置内的流场，得出了前置竖井贯流泵装置流态好的结论；徐磊[7]、周济人[8]、谢荣盛等[9]分别针对性优化设计了竖井贯流泵装置并进行了数值模拟计算及模型试验，综合性能提升。

本文以某泵站的双向竖井贯流泵装置模型为研究对象，在前人研究的基础上，运用CFD数值模拟软件对整体泵装置进行数值模拟，改变竖井流道外轮廓线以及增加直导叶方案进一步对整体泵装置进行水力性能的优化，对比分析。并通过物理模型试验验证数值模拟结果的可靠性。

1 计算模型

双向泵的叶轮直径D=2 400 mm，转速n=118 r/min，泵装置的nD值为283.2。正向排水设计流量为14 m3/s，反向引水设计流量为12.5 m3/s。泵站运行特征扬程见表1。

表1 泵站运行特征扬程Tab.1 Special running head of pump station

正向排水时竖井前置位于内河侧，出水采用直管式流道；反向引水时竖井后置。以原型泵作为数值模拟基础，泵装置总长度为32 m。泵装置内部三维流场数值模拟对象包括进水流道、叶轮、导叶、导水锥及出水流道。

2 网格划分

进水流道、导水锥以及锥管在ICEM中建模，叶轮和导叶在Turbo-Grid中进行建模。将各部件装配，得到原型泵装置三维建模图，见图1。

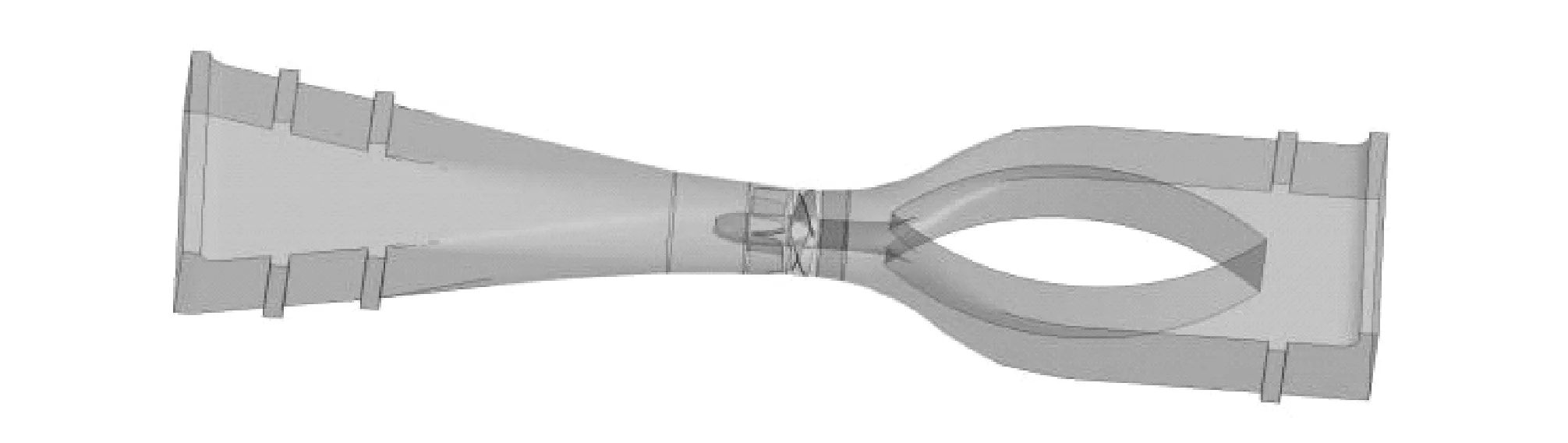
图1 竖井贯流泵装置计算模型Fig.1 Computer model of bidirectional shaft tubular pump

进水流道、导水锥以及锥管在ICEM中划分网格，其中导水锥和锥管模型采用结构化网格。叶轮和导叶在Turbo-Grid中划分网格，采用结构化网格划分，叶轮单通道网格数在12万左右，导叶单通道网格数在8万左右。竖井出水流道在UG中进行参数化建模，然后导入Mesh中进行网格划分，对边界层进行网格加密。根据参考文献[10]，为满足网格无关性要求，最终确定出水流道网格数为69.6万，导水锥网格数22.96万，锥管网格数5.7万，竖井网格数为86.62万，总网格数285万左右，网格质量均在0.4以上。不同方案网格数、网格质量均能满足计算要求。

3 边界条件

基于标准k-ε紊流模型，雷诺时均N-S方程，将进水流道的进口作为整个泵装置的进口，进口边界条件采用总压进口条件，总压设置为一个标准大气压。将出水流道的出口作为整个泵装置计算流场的出口，出口边界条件采用质量流量出口。泵装置的进、出水流道、叶轮的壳体及导叶壳体、叶片及轮毂均设置为静止壁面，应用无滑移条件，近壁区采用可伸缩壁面函数，保证模拟精度。进出水流道混凝土表面的粗糙度近似取2.5 mm。动静交界面包括叶轮和锥管之间的交界面和导叶和叶轮之间的交界面均采用速度平均的Stage交界面模型，对其余交界面使用None模型，保持流量一致。

4 优化方案

对竖井贯流泵装置的数值优化采用先整体后局部的数值分析思路，由于该泵站正向运行时，优化竖井进水流道对泵装置性能影响很小；出水流道为一般的圆变方形式，水力损失较小，优化空间有限，且出水流道土建尺寸已定，所以对出水流道不做细致优化。所以针对竖井流道反向运行时进行出水流道的优化设计是本次优化的重点。

优化设计的主要目标为设计工况下水力损失小、效率高、流线分布均匀，压力递变均匀。

水力损失计算公式为

Δh=(p2-p1)/(ρg)

(1)

式中：Δh为水力损失，m；p2、p1为出口、进口总压，Pa；ρ为水的密度，kg/m3；g为重力加速度，m/s2。

以控制尺寸为基础作为初始方案(FA1)。根据流线图改变外轮廓线，并改变外轮廓线各断面倒圆角，作为方案2(FA2)。FA1与FA2的CAD外轮廓线比较如图2所示。为保证竖井出水流道流场不至于太紊乱，在FA2的基础上在叶轮出口锥管处加入5片直导叶，作为方案3(FA3)。各方案竖井流道如图3所示。

图2 竖井出水流道方案比较图Fig.2 Comparison of shaft passage FA1 and FA2

图3 竖井出水流道图Fig.3 Shaft passage graph

4.1 反向计算结果分析

取各方案竖井出水流道壁面总压力云图，如图4所示。

图4 各工况压力对比图Fig.4 pressure comparison of different flow condition

由图4可看出，FA1压力梯度分布较大且不均匀，有明显压力先增大后减小区域，且在近竖井尖端有上下两个对称高压区，高压区速度小，易形成回流；优化后，FA2、FA3压力分布有明显改善，其中FA3压力分布最均匀，说明直导叶回收了大部分的速度环量。通过对比FA1与FA2可以看出，在改变型线后壁面压力分布均匀，竖井尖端高压区缩小，说明改变外轮廓型线是可行的；而在FA3中，高压区顶部明显缩小，底部高压区消失，说明加直导叶的整流及回收速度环量效果明显。

取各方案锥管及竖井出水流道流线图，如图5所示。

图5 各工况流线图Fig.5 Streamline chart of different flow condition

整理不同设计方案的竖井出水流道水力损失如表2所示。

由图5、表2可以看出，FA1流线紊乱呈螺旋状，在竖井两侧近壁面处有明显的速度增大区域，且整体水力损失较大；FA2流态较好，水力损失明显减小，说明通过改变流道外轮廓型线能够改善流态、减小水力损失；FA3加了5片直板后，竖井流道内流线形式最好，水流平顺无螺旋，但是锥管内平板背面出现脱流，且由于直板带来的摩擦损失增加，导致锥管内水力损失急剧增加，效率反而降低。对于这种超低扬程泵站，不适合加入直导叶。

表2 不同设计方案出水流道水力损失Tab.2 Outlet passage hydraulic loss of different design schemes

将FA1和FA2竖井出水流道从进口处(距叶轮中心长度为1.17 m)到竖井结束区域(距叶轮中心长度为13.26 m)，为保证所选取断面中有竖井流道的按每段0.93 m等分为13段(由于FA3与FA2出水流道轮廓线相同，仅比较FA1与FA2出水流道)，提取各段水力损失并进行对比。如图6所示。

图6 竖井出水流道各段水力损失Fig.6 Each section hydraulic loss of shaft passage

由图6可看出，FA2整体呈逐级减小趋势，而FA1在前半段水力损失虽低于FA2，但在6断面后出现逐步增加而后减小再增加的趋势，是由于FA1整体速度均匀、速度梯度较大，水体之间内摩擦增大造成的。单看出水竖井流道各段的水力损失曲线图，FA2方案较好。也验证了FA2的优化效果。

4.2 双向泵数值计算外特性比较

通过对不同方案各工况点进行CFD数值计算，根据计算结果，在后处理器中取出叶片上的扭矩值，进出口的压力增量值，和对应的流量，根据效率公式计算效率：

η=30ρgQH/πnM×100%

式中：η为水泵装置效率，%；Q为流量，m3/s；H为扬程，m；M为扭矩值，N/m；n为转速，r/min；ρ为水体密度，kg/m3；g为当地重力加速度，m2/s。

绘制成总体性能曲线，得到了双向竖井贯流泵装置的外特性结果并对结果进行比较。对比结果如图7所示。从图中可看出，FA2较FA1扬程与效率增加，在反向运行时，高效区明显扩大，因此，选择FA2作为最终方案是可行的。且在正向运行时改变竖井流道轮廓线并没有明显提升效率，说明就反向运行进行优化设计是可行的。经过优化后总体性能较初设方案得到了较大的上升，正向运行时，在设计流量工况下效率由71%提升至72.8%；反向运行时，效率由56.93%提升至60.66%，提升3.73%，优化效果明显。

图7 双向泵装置性能曲线 Fig.7 Hydraulic curves of bidirectional pump device

5 模型试验验证

5.1 泵装置试验系统

根据原型泵装置数值模拟的结果，将方案2的叶轮、导叶和进、出水流道加工出来进行泵装置试验研究。模型泵名义叶轮直径D=300 mm，实际叶轮直径D=299.65 mm。模型叶轮如图8(a)，轮毂比为0.4，叶片数为4，用黄铜材料经数控加工成型。模型导叶如图8(b)，轮毂直径为120 mm，叶片数为5，用钢质材料焊接成型。进出水流道采用钢板焊接制作，模型泵叶轮室和进水流道开有观察窗，便于观测叶片处的水流和汽蚀，模型泵装置如图8(c)所示。模型泵安装检查，导叶体与叶轮室定位面轴向跳动0.10 mm，轮毂外表面径向跳动0.08 mm，叶顶间隙控制在0.20 mm以内。

图8 模型试验装置图Fig.8 Model text pump decvice

5.2 测试方法

试验执行《离心泵、混流泵和轴流泵水力性能试验规范(精密级)》(GB/T 18149-2000)和《水泵模型及装置模型验收试验规程》(SL140-2006)标准，每个叶片安放角的性能试验点不少于15点，临界汽蚀余量的确定按流量保持常数，改变有效NPSH值至效率下降1%确定。

5.3 模型泵段试验结果及分析

模型泵段试验测试了5个叶片安放角度(-6°、-4°、-2°、0°、+2°)的能量性能和各叶片角度下不同流量点的汽蚀性能，将所得数据整理画成模型综合特性曲线图，按水泵相似律公式换算为原型泵综合特性曲线图，公式为：

(2)

式中：Qp为原型泵流量，m3/s；Qm为模型泵流量，m3/s；Hp为原型泵扬程，m；Hm为模型泵扬程，m；Dp为原型泵直径，m；Dm为模型泵直径，m；np为原型泵转数，r/min；nm为模型泵转数，r/min。

性能图9为模型泵转化为原型泵的综合特性曲线图。

图9 原型泵装置性能曲线图Fig.9 Archetype pump device performance curves

根据图9原型泵装置正反向综合特性曲线可知：正向最高效率点出现在-4°，流量12.792 m3/s，扬程为1.470 m，效率为73.36%；反向最高效率点出现在-6°，流量9.747 m3/s，扬程为1.434 m，效率58.7%。

为证明数值模拟计算的可靠性，取-2°的数据结果与数值模拟进行对比，如图10所示。

图10 试验结果与数模结果对比图Fig.10 Comparison of simulation results and experiment results

由图10正反向运行装置性能对比图可看出：正向运行时，试验最高效率为72.6%，数模最高效率为72.8%，误差为0.3%；反向运行时，试验最高效率为58.34%，数模最高效率为60.66%，误差为3%，满足工程应用要求。正向运行时，竖井前置，导叶后置，可以有效地回收大部分速度环量，泵装置整体效率较高；竖井后置工况，不存在后置导叶，速度环量较大，动能回收率低，泵装置扬程低，出水流道损失较大，泵装置的性能偏低。试验测试过程中，通过测试进出口的压力值，计算装置扬程。对于有后导叶的竖井前置装置而言，导叶回收速度环量，动能较小，正向吻合较好。竖井后置作为出水流道时，速度环量较大，泵装置出口动能较大，试验中损失较大。因此反向运行时，试验扬程较数值模拟要低。这跟参考文献[9,11]情况相同，这种现象也是今后要着重分析的。整体而言试验曲线与数值模拟曲线趋势一致，数值模拟具有一定的可信度。

6 结 语

(1)基于RNGk-ε紊流模型，雷诺时均N-S方程，采用CFD数值模拟进行了三维流场数值模拟优化，进行对比分析最终确定了最优方案。最优方案比原方案流态平整，水力损失下降12.6%，正向效率提高1.8%，反向效率提高大于3%，说明优化效果明显。

(2)改变竖井出水流道的外轮廓线对出水流道的水力损失有较大影响；在超低扬程的竖井贯流双向泵站中，不宜采用在反向叶轮出口增加直导叶的方法。

(3)数值模拟结果与模型试验结果趋势一致，说明采用数值模拟与试验设计相结合的方法来优化设计竖井贯流泵装置是可行的。

□

[1] 刘 超.轴流泵系统技术创新与发展分析[J].农业机械,2015,45(6):49-59.

[2] 谢伟东,蒋小欣,刘铭峰,等.竖井式贯流泵装置设计[J].排灌机械,2015,23(1):10-12.

[3] 刘 军.竖井式贯流泵装置水力特性及优化设计研究[D].江苏扬州:扬州大学,2009.

[4] 陈荣新,关醒凡,王 伟,等.双向竖井贯流泵站模型泵装置模型试验[J].排灌机械,2007,25(1):33-37.

[5] 陈会向,周大庆,张蓝国,等.基于CFD的双向竖井贯流泵装置水力性能数值模拟[J].水电能源科学,2013,31(11):183-187.

[6] 刘 君,郑 源,周大庆,等.前、后置竖井贯流泵装置基本流态分析[J].农业机械学报,2010,41(增刊):32-38.

[7] 徐 磊,陆林广,陈 伟,等.南水北调工程邳州站竖井贯流泵装置进出水流态分析[J].农业工程学报,2012,28(6):50-56.

[8] 周济人,汤方平,石丽建,等.基于CFD的轴流泵针对性设计与试验[J].农业机械学报,2015,46(8):42-47.

[9] 谢荣盛,吴 忠,何 勇,等.双向竖井贯流泵进出水流道优化研究[J].农业机械学报,2015,46(6):49-59.

[10] 杨 帆.低扬程装置水动力特性及多目标优化关键技术研究[D].江苏扬州:扬州大学,2013.

[11] 金 燕,刘 超,汤方平.灯泡贯流泵装置内部流动数值模拟 [J].排灌机械工程学报,2010,28(2):155-159.