水电机组基于贝叶斯网络的故障树故障诊断分析研究

胡勇健，肖志怀

(1.深圳蓄能发电有限公司，深圳 518115；2.武汉大学动力与机械学院，武汉 430072)

0 引 言

由于组成构件之间及构件内部存在很多不确定关系，各种可能的因素充斥其间，使得故障诊断在大型设备领域应用中准确率比较低下，导致故障原因不易确定。因此如何从众多不确定信息中获得最终的最有可能的故障原因是故障诊断领域发展所需要克服的主要问题。

目前利用故障树分析法建造模型进行故障诊断是最常用的，但这种模型却存在一些局限性，表现为：处理不确定性问题能力有待提高、多源信息表达与融合能力相对较弱。然而近年来受到越来越多关注和研究的贝叶斯网络，不仅从其推理机制和系统状态描述看，与故障树存在很大的相似之处；而且还可以描述事件之间不确定的故障逻辑关系，事件状态多样性的能力；并且贝叶斯网络特有的双向推理机制在故障诊断分析中具有明显优势[1]。因此，许多专家学者对贝叶斯网络都进行了相关研究：文献2将基于贝叶斯网络的故障树应用到机械设备中，文献3研究了基于故障树的贝叶斯网络建造方法与故障诊断应用，文献4研究了基于故障树与贝叶斯网络的钻井井塌事故的定量分析，文献5研究了基于故障树贝叶斯网络的装备故障诊断方法，文献6利用故障树与贝叶斯网络对采煤机进行了故障可靠性分析。

与采用贝叶斯网络方法相比，如果采用故障树分析方法计算系统的事件发生概率，首先需要进行定性分析得到该系统所有的最小割集，然后再利用容斥定理进行精确计算，或用独立近似方法进行近似计算[7]，过程比较繁琐；而采用贝叶斯网络模型中的概率推理则可以在获取网络模型结构中节点间的相互影响程度后，直接利用贝叶斯网络原理进行数学计算，用概率的形式表达和比较各个节点在系统出现故障时产生影响的程度，确定导致系统故障的可能原因。

本文将贝叶斯网络引入到水轮发电机系统故障诊断模型中，利用贝叶斯网络模型反向推理机制结合桶排除法给出发电机故障后验概率的计算方法，并通过简单算例比较贝叶斯网络和故障树分析算法，验证该算法计算结果的有效性，最后通过计算发电机故障后验概率与先验概率的对比，给出故障时各个事件概率变化情况进行诊断，验证贝叶斯网络方法的可行性和合理性。

1 故障树分析法与贝叶斯网络模型

1.1 故障树分析法

故障树分析法是一种图形演绎由果到因、自上而下的逻辑分析方法，通过分析可能造成目标故障的各种因素，画出逻辑图形成故障树展示目标与因素之间的内在联系，再对目标系统中实际发生的故障事件，做出由顶至底按树状逐级细化的分析。其目的是判明基本故障、确定故障原因、故障影响和发生概率等，是一种简单可靠而又行之有效的系统故障诊断方法[8]。其过程可概括为：从某一故障事件开始，找出导致该事件发生的各个直接因素，然后对找出的因素分别寻找其各自的直接原因，重复执行该过程，直至把形成设备故障的基本事件分析出来为止[9]。依照此方法分析系统发生故障的各种途径和影响因素，然后对各基本事件赋予概率值，就可以用故障树模型进行诊断决策。故障树结构由3种符号构成：事件符号、逻辑门符号、转移符号。事件符号用于表示各种顶事件、中间事件和底事件；逻辑门符号用于表示各事件之间的逻辑关系；转移符号则主要是为使图形简明、避免重复绘图而设置的符号。应用故障树模型一般需要做出假设：

(1)事件只有两种状态，即正常或故障；

(2)各个事件是彼此独立的，不会产生相互间的影响联系，即事件间存在条件独立性；

(3)故障和导致该故障的因素连接关系是通过逻辑门来表达的，包括与门(AND)、或门(OR)、非门(NOT)、异或门(XOR)等。

简单的故障树结构如图1所示。

图1 简单的故障树结构Fig.1 Simple fault tree structure

1.2 贝叶斯网络模型

贝叶斯网络是一种基于网络结构的有向图解描述，用具有网络结构的有向图表达各个信息要素之间的关联关系：用节点表示各个事件要素，用连接节点之间的有向边表示各个事件要素的关联关系，用条件概率表示各个事件要素之间的影响程度[10,11]。贝叶斯网络本身将多种事件关联关系可视化为一种概率依赖图形模型，更加直观的表明事件变量之间的因果和连接强度；同时贝叶斯网络可在不完整的有限的信息条件下进行推理和学习，在解决不确定性问题方面具有很大的优势。总的来看，贝叶斯网络理论方法运用了一种反复学习的思想，首先使用通过领域专家知识指定的先验概率表示节点间的不确定性关联关系和连接强度，并将后来获取到的数据进行处理，利用概率规则来对之前已经指定的先验概率重新调整，使之更加贴合实际情况。

贝叶斯网络模型描述的随机变量间概率依赖关系，可表示为二元组B=，包括两部分：

(1) 具有n个节点的有向无环图G。G=是一个有向图网络结构，其结点为X={x1,x2,…,xn}，n≥1，A是弧的集合。网络结构中节点代表事件变量，节点间的弧A代表相互关联关系；

(2)节点相关的条件概率表P。条件概率可以用p(Vi|Pa(Vi))(Pa(Vi)是Vi的父结点，在G中的两个相互连接的节点对A→B中，A称为B的父节点，B称为A的子节点)来表示。结构中任意节点的任何一种概率都可以看作是在一定先验知识下的条件概率。

(1)

式中：p(A)为A的先验概率；p(A/B)为A的后验概率。 先验概率往往是根据以往的经验分析总结得到的概率，后验概率指在获得一定的事实条件信息下对节点概率进行修正后的概率。

如果A存在n种状态a1,a2,…,an，那么贝叶斯网络的全概率公式定义:

p(B)=∑p(B/A-ai)p(A=ai),i=1,2,3,…,n

(2)

2 故障树与贝叶斯网络模型的比较

2.1 故障树转化贝叶斯网络模型方法

比较发现贝叶斯网络与故障树的组成结构是相互对应的，根据故障树的结构，可以将故障树转换成贝叶斯网络模型：故障树中每个基本事件和逻辑门输出事件对应贝叶斯网络的各层节点，逻辑门对应连接叶斯网络的各层节点的有向边，故障树的逻辑关系可以通过改变贝叶斯网络的条件概率表来实现表达[12]。具体的转化对应关系如图2所示。

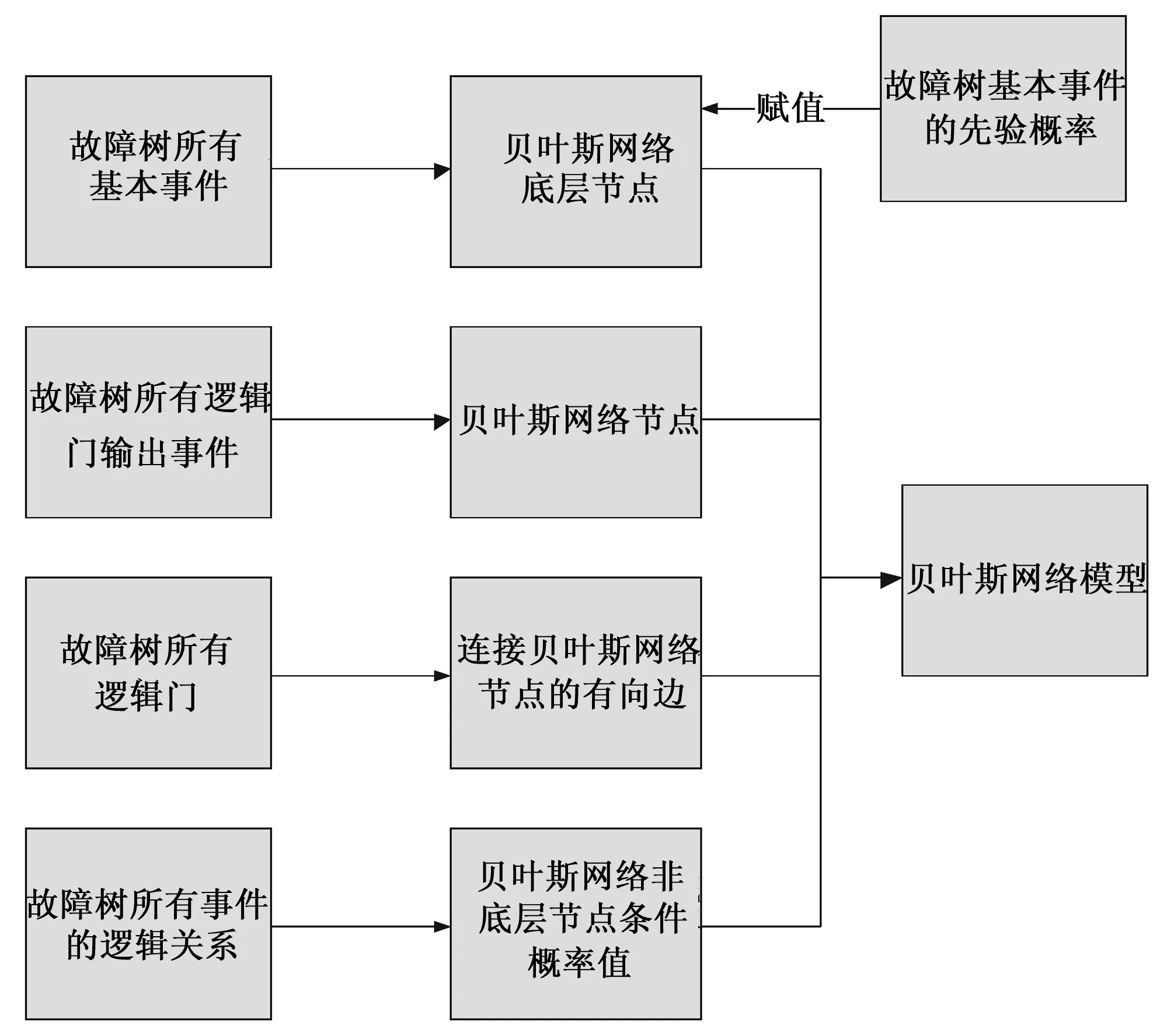
图2 故障树与贝叶斯网络模型对应关系Fig.2 Correspondence between fault tree and Bayesian network model

现以图3所示的简单故障树结构为例进行说明，转化后的贝叶斯网络模型及相关的逻辑连接关系如图4所示，假设故障树中各设备的状态只有两种：正常(0)和故障(1)。

图3 与或门故障树Fig.3 Gate fault tree

图4 转化后的贝叶斯网络图Fig.4 Transformed Bayesian Networks

2.2 故障树与贝叶斯网络分析方法对比

以图3和图4为例，利用故障树方法和贝叶斯网络方法计算两种模型相同顶层事件 的故障发生概率，假设：

p(X1)=(0.95，0.05)

p(X2)=(0.92，0.08)

p(X3)=(0.91，0.09)

(1)故障树方法：根据最小割集定义，分析得出此简单系统的最小割集为{X1,X3},{X2,X3}，运用不交化原理的计算过程可以得到顶事件T=1的发生概率为：

p(T=1)=p(X1=1)·p(X3=1)+p(X2=1)·p(X3=1)-

p(X1=1)·p(X2=1)·p(X3=1)=0.011 34

(3)

(2)贝叶斯网络方法：根据贝叶斯网络全概率公式可知，顶层事件T=1的全概率公式为：

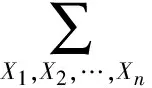
(4)

结合图3故障树模型经转化至贝叶斯网络模型图4中的“与、或”关系，可以得到：

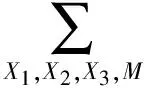
p(X3=1)·[1-p(X1=0)·p(X2=0)]=0.011 34

(5)

比较式(3)和式(5)，显然这两种计算方法的过程存在差异，结果相同。如果对一些结构复杂、逻辑门多样的故障树进行分析时，采用故障树分析法首先需要找出系统所有最小割集再运用不交化原理进行计算，是一个繁琐的计算过程；然而将其转化成贝叶斯网络模型后就可以运用条件概率公式和全概率公式计算获得顶事件的发生概率，避免了最小割集的求解，分析过程将变得较为方便简单。

3 发电机故障诊断分析

水轮发电机是将水的机械能转化为电能的重要机组设备，在运行时受到众多因素的影响，容易导致故障的发生，所产生的故障又大多是相互关联、相互影响的，因此难以有效分析确定出故障发生的原因。通过总结实际运行中的发电机故障，常出现以下几种类型的故障：定子机座振动、定子铁芯及绕组故障引起的定子故障；转子铁芯及绕组引起的转子故障；发电机电磁不平衡以及转子质量不平衡引起的发电机动不平衡；转频及极频振动引起的电磁振动。在对水轮发电机的各种故障机理进行分类后，按照一定的逻辑门关系构建了一个简单的由“或门”连接的水轮发电机故障树结构。其故障树结构如图5所示：

图5 发电机故障树结构模型Fig.5 Generator fault tree model

假设故障树结构中各个底层事件之间是相互独立不产生相互影响的，并且整个系统和系统中所包含的事件都只有两种状态：正常(0)和故障(1)。根据专家系统获得各个底层事件的先验概率分布为：

p(X1)=(0.980 4，0.019 6)

p(X2)=(0.998 7，0.001 3)

p(X3)=(0.993 5，0.006 5)

p(X4)=(0.995 7，0.004 3)

p(X5)=(0.995 5，0.004 5)

p(X6)=(0.994 4，0.005 6)

p(X7)=(0.996 4，0.003 6)

p(X8)=(0.997 7，0.002 3)

p(X9)=(0.998 6，0.001 4)

依据图2所示的转化对应关系将图5所示的发电机故障树模型结构转化为贝叶斯网络模型结构，建立发电机故障贝叶斯网络结构模型如图6所示，其中同一层的节点均是通过“或门”与上一层节点相连接。

图6 转化后的贝叶斯网络模型Fig.6 Transformed Bayesian network model

利用桶排除法，结合贝叶斯网络的正向推理能力、全概率公式和贝叶斯网络节点之间的相互联系可以计算出顶层事件“发电机故障T”的发生概率:

p(S1=0)=p(X1=0)·p(X2=0)·p(X3=0)=0.972 8

p(S1=1)=1-p(S1=0)=0.027 2

同理可以求得

p(S2)=(0.991 2，0.008 8)

p(S3)=(0.990 8，0.009 2)

p(S4)=(0.996 3，0.003 7)

p(T)=(0.951 8，0.048 2)

即在此种专家系统确定的系统底层各个事件故障概率情况下，系统顶层节点发电机发生故障的可能性为0.048 2。

同时贝叶斯网络又具有反向推理的能力，可以算得在整个系统顶层节点发电机出现故障的情况下底层各个节点的后验概率分别为：

p(X1=1/T=1)=

0.406 6

p(X2=1/T=1)=0.027 0

p(X3=1/T=1)=0.134 9

p(X4=1/T=1)=0.089 2

p(X5=1/T=1)=0.093 4

p(X6=1/T=1)=0.116 2

p(X7=1/T=1)=0.074 7

p(X8=1/T=1)=0.047 7

p(X9=1/T=1)=0.029 0

将计算获得的各个底层节点的后验概率与先验概率进行柱状图分析，结果如图7所示。

图7 各底层节点的先验概率与后验概率对比Fig.7 Comparison of the prior probability and the posterior probability of each node

由图7可以看出，当系统发生故障时，节点X1即定子绕组故障的后验概率变化最为显著，其他的X3节点和X6节点变化也较大，因此在此种专家系统确定的各个节点的先验概率条件下，如果发电机系统出现了故障，首先需要查看的节点即为X1定子绕组故障。当然此种诊断推理结果会一定程度上依赖专家系统确定的先验概率情况，但依旧可以说明故障树模型结构转化为贝叶斯网络模型在复杂故障诊断领域的可行与合理性。

5 结 论

通过简单与或门故障树算例，验证了贝叶斯网络正向推理方法与故障树分析方法的计算结果是相同的，然后将贝叶斯网络引入到发电机故障诊断分析中，其核心是将故障树转化建立贝叶斯网络模型，利用贝叶斯网络全概率公式和条件概率公式反向推理，用概率的形式表示出系统发生故障时各部件故障的可能性，对比之前通过专家系统确定的先验概率，得到最有可能发生故障的底层事件，据此对系统故障进行诊断，对大型复杂系统的故障诊断具有指导意义。

□

[1] 张晓丹. 汽车发动机故障诊断中不确定性问题的贝叶斯网络解法[D]. 东北大学, 2005.

[2] 杨 虹, 汪厚祥, 支冬栋,等. 基于贝叶斯网络的故障树在机械设备中的应用[J]. 微计算机信息, 2010,26(4):115-117.

[3] 李俭川, 胡茑庆, 秦国军,等. 基于故障树的贝叶斯网络建造方法与故障诊断应用[J]. 计算机工程与应用, 2003,39(24):225-228.

[4] 李 盼, 樊建春, 刘书杰. 基于故障树与贝叶斯网络的钻井井塌事故的定量分析[J]. 中国安全生产科学技术, 2014,(1):143-149.

[5] 齐善明, 李 磊, 杨 欢. 基于故障树贝叶斯网络的装备故障诊断方法研究[J]. 舰船电子工程, 2012,32(6):112-114.

[6] 古海龙, 刘混举. 基于故障树与贝叶斯网络的采煤机故障可靠性分析[J]. 煤炭技术, 2015,34(3):242-244.

[7] 陈东宁, 姚成玉, 王 斌. 贝叶斯网络在液压系统可靠性分析中的应用[J]. 液压与气动, 2012,(7):58-61.

[8] 宫义山, 高媛媛. 基于故障树和贝叶斯网络的故障诊断模型[J]. 沈阳工业大学学报, 2009,31(4):454-457.

[9] 张 燕, 佘 维, 李 平. 基于Petri网和故障树的电力系统故障诊断模型[J]. 计算机测量与控制, 2015,23(8):2 626-2 628.

[10] Stephenson T A.An introduction to Bayesian network theory and usage[R].Swizerland: IDIAP-RR 00-03,DaleMolle Institute,2000.

[11] Bresnick T A, Buede D M, Tatman J A. Introduction to Bayesian network[C]∥The 66th MORS Symposiam, California; Naval Postgraduate School Monterey, 1998:23-25.

[12] 周忠宝, 周经伦, 金 光,等. 基于贝叶斯网络的概率安全评估方法研究[J]. 系统工程学报, 2006,21(6):636-643.