台阶式溢洪道流速水头沿程变化研究

于进伟，刘韩生

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

台阶式溢洪道是随着碾压混凝土筑坝技术发展起来的一种消能设施，一方面在施工过程中可使大坝一次碾压成型，缩短工期；另一方面利用台阶消减水流能量，大幅缩短消力池长度，在国内外水利工程中得到广泛应用[1,2]。各国专家对台阶结构的水力特性做出大量研究，研究成果颇为丰富。例如，陈群等[3]研究表明θ=51.3°时消能率随相对台阶高度的变化出现波动现象，且台阶高度对消能率的影响与单宽流量有关，单宽流量小，台阶高度变化对消能率影响大。Rice[4]指出台阶溢洪道的消能率随坡面流程长度的增长而增大，可显著减小消力池的长度。Yildiz[5]研究表明溢洪道坡度小于51.3°消能率随台阶高度增加而增大；坡角大于60°时，台阶高度对消能率几乎无影响。Tabari[8]通过模拟分析得出坝高相同时，消能率随台阶高度减小而降低。田嘉宁等[9]通过模型试验得出消能率随相对坝高增加而增大，随坡度变陡减小。此外，众多研究[3～4,6～9]表明消能率随单宽流量的增大而降低。为了进一步的探索台阶式溢洪道的水力特性，更好的体现台阶溢洪道的优势，本文针对台阶水流的单位重量液体具有的动能进行一系列研究。

考虑到光滑溢洪道的水力计算比较成熟，各水力参数可通过试算求得，本文将台阶式溢洪道和同体型的光滑溢洪道的流速水头进行比较，引入相对流速水头的概念，阐述其物理意义。通过多组模型试验、采用单一变量法研究流速水头、相对流速水头与流程长度L、单宽流量q、台阶高度d、坡度θ的关系,以此论证了引入台阶溢洪道相对流速水头的必要性。

1 相对流速水头的定义

流速水头是水流能量的重要组成部分，也是重要的水力指标，为探究台阶结构对溢洪道流速水头的影响，本文引入相对流速水头的概念。定义光滑溢洪道与同体型台阶式溢洪道对应断面的流速水头之差为相对流速水头。相对流速水头大，说明光滑溢洪道超过台阶溢洪道流速水头的差值越大，则台阶部分对水流的阻碍效果好，越有必要采用台阶式溢洪道。

根据定义，任意断面处的相对流速水头：

式中：v22/2g表示光滑溢洪道的流速水头；v21/2g表示同体型台阶式溢洪道相同断面的流速水头，如图1。台阶溢洪道的水力参数通过模型试验测得，光滑溢洪道通过连续方程、能量方程试算出渐变水流的流速。

图1 溢洪道示意图Fig1 Sketch of a stepped spillway and a smooth chute

2 试验简介

为探究台阶式溢洪道流速水头的规律特性，本文对四个工程项目的台阶溢洪道进行水工模型试验，台阶溢洪道均按重力相似准则进行模型设计。过流流量采用三角堰或矩形薄壁堰测量；断面平均流速使用毕托管流速仪测量或单宽流量与断面平均水深的比值计算；试验流态为紊流。L为台阶流程长度，即测点位置到起始台阶起点的斜线距离。台阶溢洪道的基本试验资料见表1，几何参数示意图见图1。

3 试验结果分析

3.1 流速水头与单宽流量的关系

为探究单宽流量与相对流速水头的关系，选取坡度为38.7°、台阶高度为1.0 m的台阶溢洪道进行模型试验，在21.20、35.72、46.67、62.18 m2/s四种单宽流量下进行数据分析。

表1 模型试验基本资料Tab.1 Basic information of hydraulic models

图2、图3分别绘制了四种单宽流量下台阶流速水头、相对流速水头与流程长度的关系。由图2可知，非均匀流段下台阶流速水头均表现为先增大后减小的趋势，不便分析应用。四种单宽流量下相对流速水头与流程长度均呈现出线性递增规律，相关系数R2在0.994 8～0.997 8之间。其中最大、最小单宽流量对应的直线斜率分别为最小、最大值0.406 4、0.482 8，四条直线斜率的最大相对误差5.05%，表明相同断面位置处，单位流程长度上单宽流量小对应的相对流速水头大。根据相对流速水头的物理意义可知，台阶部分对水流产生的阻碍作用沿程表现为线性递增规律，单位宽度单位流程的水头损失为定值。相对流速水头与流程长度规律性强，便于应用。

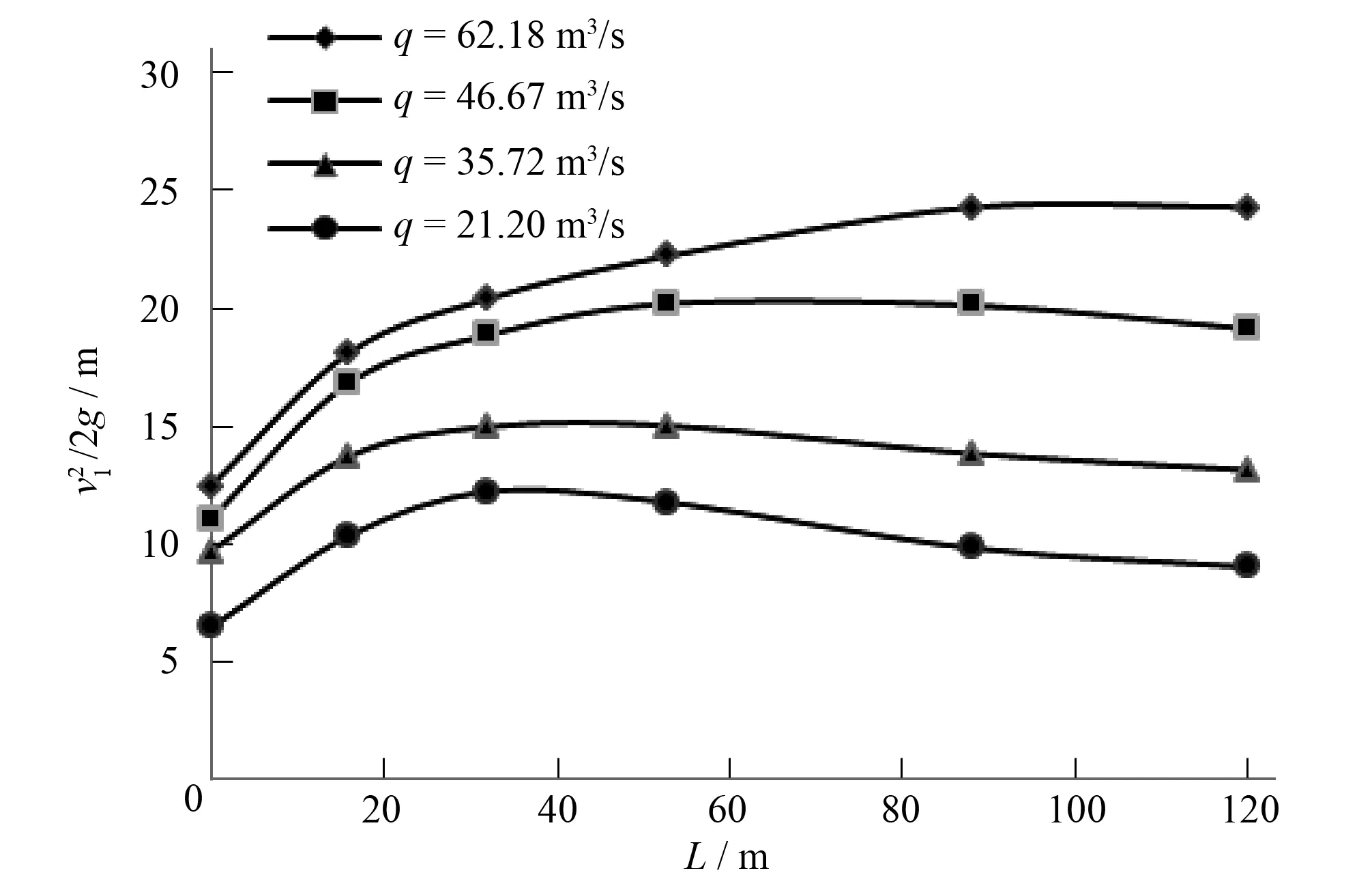
图2 不同单宽流量下v21/(2g)～L关系Fig.2 Relations of v21/(2g)～L at different unit width discharge (h=1.0 m，θ=38.7°)

图3 不同单宽流量下Δv2/(2g)～L关系Fig.3 Relations of Δv2/(2g)～L at different unit width discharge(h=1.0 m，θ=38.7°)

3.2 流速水头与台阶高度的关系

为研究台阶高度与相对流速水头的关系，选取坡度为38.7°，台阶高度分别为0.5、1.0、2.0 m三种台阶结构的溢洪道，在单宽流量为35.72 m2/s进行模型试验。

由图4可知，同坡度不同台阶结构的溢洪道，非均匀流段台阶的流速水头沿程亦表现为先增大后减小的曲线规律，但是曲线的沿程变化位置、变化幅度与台阶高度的关系均无规律可循。图5分析可知，不同台阶高度相对流速水头与流程长度均表现为良好的线性关系，相关系数在0.996 6～0.998 2之间，其他工况也满足此规律。在单宽流量35.72 m2/s的工况下，0.5、1.0、2.0 m台阶高度对应的直线斜率分别为0.436 8、0.459 6、0.494 4，最大相对误差7.57%。根据相对流速水头的物理意义可知，同一体型的光滑溢洪道和台阶溢洪道在相对流速水头上沿程表现为线性递增规律，且相同断面位置，台阶高度较高对应的相对流速水头高。因此坝高和单宽流量一定时，适当的增加台阶高度，可增强台阶部分对水流的阻碍效果，但变化幅度有限。

图4 不同台阶高度下v21/(2g)～L关系Fig.4 Relations of v21/(2g)～L at different step heights (q=35.72 m2/s，θ=38.7°)

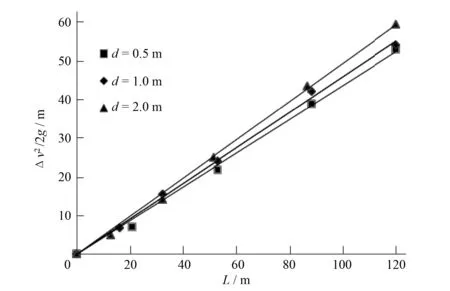
图5 不同台阶高度下Δv2/(2g)～L关系Fig.5 Relations of Δv2/(2g)～L at different step heights (q=35.72 m2/s，θ=38.7°)

3.3 流速水头与坡度的关系

为探究坡度与相对流速水头的关系，选取台阶高度为1 m，坡度分别为26.6°、33.7°、38.7°、48.0°四种体型的台阶溢洪道，在单宽流量为35.72 m2/s进行模型试验。

图6和图7分别绘制了四种坡度下台阶流速水头、相对流速水头与坡度的关系。不同坡度下台阶流速水头总体上仍表现为先增大后减小的趋势曲线规律，由于台阶水流的复杂性，变化规律复杂。而不同坡度对应的相对流速水头与流程长度均呈现良好的线性递增规律，相关系数R2在0.995 9～0.998 8之间。在台阶高度1.0 m、单宽流量为35.72 m2/s的工况下， 26.6°、33.7°、38.7°、48.0°四种坡度的台阶溢洪道对应的直线斜率分别为0.233 3、0.328 9、0.459 5、0.858 3，最大和最小斜率相差0.625 0，最小相对误差为39.7%。与单宽流量、台阶高度相比，坡度对相对流速水头的影响最显著；且相同断面位置处单位流程长度的相对流速水头随坡度增加而增大。根据相对流速水头的物理意义可知，溢洪道坡度在26.6°～48.0°之间，坡度较大时，台阶结构对水流的阻碍作用越明显，越有必要使用台阶式溢洪道。

图6 不同坡度下v21/(2g)～L关系Fig.6 Relations of v21/(2g)～L at different slopes(q=35.72 m2/s, h=1.0 m)

图7 不同坡度下Δv2/(2g)～L关系 Fig.7 Relations of Δv2/(2g)～L at different slopes(q=35.72 m2/s, h=1.0 m)

4 结 语

本文以台阶溢洪道非均匀流段的流速水头为研究对象，并与光滑溢洪道进行对比，引入了相对流速水头的概念。研究成果如下：

滑行水流非均匀流段台阶的流速水头沿程呈现出先增大后减小的曲线规律，规律复杂，不便应用；相对流速水头与流程长度呈现良好的线性递增规律，相关系数R2在0.994 8～0.998 8之间。其规律性强，便于应用，论证了引入相对流速水头的必要性。

单宽流量、台阶高度、坡度均对相对流速水头有一定影响，其中坡度的影响最显著。台阶相对流速水头随单宽流量的减小而增大，而与台阶高度、坡度呈递增关系。说明适当增加台阶高度可增强台阶部分对水流的阻碍作用；在小单宽流量、坡度较陡时更有必要采用台阶式溢洪道。

□

[1] 艾克明. 台阶式泄槽溢洪道的水力特性和设计应用[J]. 水力发电学报, 1998,17(4):86-95.

[2] 吴宪生. 台阶溢流坝的应用评述[J]. 四川水力发电, 2005,24(1):22-26.

[3] 陈 群,戴光清,朱分清,等. 影响阶梯溢流坝消能率的因素[J]. 水力发电学报, 2003,22(4):95-114.

[4] Rice C E, Kadavy K C. Model study of a roller compacted concrete stepped spillway[J]. Journal of Hydraulic Engineering, 1996,122(6):292-297.

[5] Yildiz D, Kas I. Hydraulic performance of stepped chute spillways[J]. Hydropower and Dams, 1998,(4):64-70.

[6] Ohtsu I, Yasuda Y, Takahashi M. Flow characteristics of skimming flows in stepped channels[J]. Journal of Hydraulic Engineering, 2004,130(9):860-869.

[7] Shahheydari H, Nodoshan E J, Barati R. Discharge coefficient and energy dissipation over stepped spillway under skimming flow regime[J]. KSCE Journal of Civil Engineering, 2015,19(4):1 174-1 182.

[8] Tabari M M R, Tavakoli S. Effects of Stepped Spillway Geometry on Flow Pattern and Energy Dissipation[J]. Arabian Journal for Science and Engineering, 2016,41(4):1 215-1 224.

[9] 田嘉宁，安田阳一，李建中. 台阶式泄水建筑物的消能分析[J]. 水力发电学报, 2009,28(2):96-100,127.