沿程泄流多孔管道出流能力计算
金 瑾,刘焕芳,王亚朦
(石河子大学水利建筑工程学院,新疆 石河子 832003)
沿程泄流多孔管是将管道侧壁沿程开孔,水流经小孔沿轴向均匀流出,简称多孔管,实际工程中出流的孔口也可以连接喷嘴或是长度较小的管道。多孔管的应用范围广泛,常见于农业水利工程中的喷灌滴灌系统,给排水中的输配水工程等等,国内外学者对多孔出流问题进行了大量的研究[1-7]。这类设备的操作状况、经济实用性主要取决于流体出流的均匀程度[8-10]。所以,研究多孔管的出流性能具有实际的工程价值[7,10-13]。
多孔管出流理想的情况是所有孔口(或滴头)的出流量完全相同,但这种理想情况实际上是不可能发生的,原因在于沿程孔口(或滴头)有液体流出,管内液流属变质量流动,孔口(或滴头)的出流量必然会受到管内压力沿程变化的影响。以往的研究结果表明,孔口出流量q与工作压力水头h的关系为q=chy,c为滴头流量系数,y为流态指数,流量对压力变化的敏感性取决于流态指数y的大小[14]。前人对c和y进行了大量实验[15,16],得到了一些经验公式。但这些研究成果没有给出管道总出流量公式,也没有给出管长L、管径D、滴孔间距S及管道坡度I等因素和q的关系表达式。针对此问题,本文在假定多孔管开孔率、长径比和管道坡度对多孔管流量折减系数的影响是相互独立的基础上,根据试验结果拟合了多孔管流量折减系数的计算公式,建立了多孔管的总出流量Q0和平均单孔出流量计算公式。将公式计算结果和具体试验数据进行对比验证,结果表明二者吻合情况较好,为该公式在实际工程中的应用提供了理论依据。
1 多孔管总出流量计算基本公式
对于侧壁没有开孔的简单管道,列能量方程可得自由出流条件下管道流量Qz为[17]:
(1)
式中:A0为管道过水断面的面积;D为管径;λ0为管道沿程水头损失系数;Lz为管长;∑ζ为管道系统的局部水头损失系数之和;μz为流量系数;g为重力加速度;H为管道入口的压力水头。
从式(1)可知,自由出流条件下简单管道的出流量与管长、管径、作用水头、管道沿程水头损失系数和局部水头损失系数有关。
对于多孔管,也可以列能量方程,得到多孔管总出流量Q0为:
(2)
式中:p0为多孔管的相对动水压强;γ为水的密度。
对比式(1)和式(2)可知,在H、Lz、D、λ0和ζ相同的条件下,二者的不同之处在于根号里面的有效水头,多孔管的有效水头减少了p0/γ,在保证多孔管正常工作的前提下p0/γ为一正值,可知(H-p0/γ) 在多孔管出流时,一定有0 (3) 式中:ψ称为流量折减系数。 对比式(1)和式(3)不难发现ψ是沿程多孔泄流管道的总出流量与自由出流管道出流量的比值,那么计算多孔管的总出流量时可先根据式(1)计算对应的自由出流简单管道的出流量,将所得结果乘以流量折减系数即得多孔管的总出流量,因此如何根据多孔管的相关参数确定流量折减系数是关键问题之所在。 研究表明,多孔管的出流量Q0与H、D、L、S、d、I、ρ、g、υ及σ等因素有关,其中d为滴孔直径,υ是液体运动黏滞系数,σ为液体表面张力系数。Q0与各个变量的函数关系可用下式表示[17]: Q0=f1(H,g,ρ,D,d,S,L,I,υ,σ) (4) 根据量纲和谐原理,可得多孔管流量用无量纲数表达的关系式为: (5) 同样可得相应的自由出流简单管道流量关系表达式为: (6) 对比式(5)、式(6),结合式(3)可得多孔管流量折减系数ψ的表达式为: (7) (8) 将η定义为多孔管的开孔率。 式(7)中d/D、d/S均为开孔率η对多孔管的影响,所以式(7)可改为: ψ=f4(η,E,I) (9) 式中:E定义为多孔管的长径比。 由以上结果可知ψ与η、E和I有关,想要确定流量折减系数的具体计算表达式还必须通过相关实验来获得。 2.2.1 实验概况 如图1所示,该实验装置主要由蓄水池、水表、闸阀和多孔管组成,蓄水池左端的溢流板保证了多孔管内的水流为恒定流,通过调整溢流板的高度可调节多孔管的作用水头H,AB为双侧等间距均匀开孔的多孔软管,实验时在不同小孔处连接测压管可测出该位置的压力水头,利用秒表和量筒可量测多孔管不同单孔的出流量。 图1 多孔管模型试验装置示意图Fig.1 The testing device diagram of the porous pipe 注:1-蓄水池;2-水表;3-闸阀;4-多孔管;5-出口测压孔。 室内模型实验的主要变化参数有:L、H、S、I等,具体的实验参数变化见表1。假设这些影响因素对多孔管流量折减系数ψ的影响是相互独立的,则式(9)可写为: ψ=f5(η) f6(E) f7(I) (10) 通过对实验数据的分析研究,得到了多孔管流量折减系数与I、E和η之间的关系,具体结果如下。 2.2.2 铺设坡度影响规律 图2为多孔管η和E保持不变I和ψ的关系图,由图2中结果可知:其他条件不变的情况下流量折减系数ψ和管道坡度成线性增加的关系,说明在只改变管道坡度时多孔管总出流量随坡度的增加而增加。结合具体的实验参数:L=50 m,D=4.775 cm,S=0.15 m,H=0.4 m,根据实际数据拟合可知 ,根据式(10)可得: ψ=(0.575 7+22.141I)f5(η)f6(E) (11) (12) 图2 ψ与I的关系Fig. 2 The relation of ψ and I 2.2.3 长径比影响规律 图3所示为多孔管D=3.5 cm,I=0.1%,S=0.3 m,D0=3.5 mm,L0=50 m(D0和L0为某一确定的多孔管管径和管道铺设长度),在H=0.4 m作用下管道相对长径比E/E0与ψ1的关系(其中E0=L0/D0)。由图3中结果可知其他条件不变的情况下流量折减系数ψ1随着长径比增加而增加,但呈非线性关系,即多孔管总出流量随着长径比的增加而增加。数据拟合的结果为: 结合式(12)可得: 或 ψ2= (14) 图3 ψ1与E/E0的关系Fig.3 The relation of ψ1 and E/E0 2.2.4 开孔率影响规律 根据式(8)定义某一多孔管的开孔率η0=d20/(2D0S0),本文取d0=1.2 mm,D0=3.5 cm,S0=30 cm,研究η和ψ之间的关系。图4为只改变开孔率时相对开孔率η/η0与流量折减系数ψ2的关系。由实验数据结果可知,开孔率越大流量折减系数也越大,但呈非线性关系,即多孔管总出流量随着开孔率的增加而增加。拟合结果为: (15) 图4 ψ2与η/η0的关系Fig.4 The relation of ψ2 and η/η0 将式(15)代入式(14),整理可得: ψ=0.851 5 (1+38.46I) × (16) 再把E和η的表达式代入式(16),可得多孔管流量折减系数的计算式为: ψ=0.851 5 (1+38.46I) × (17) 最后将式(17)代入式(3),可得多孔管的总出流量的计算公式: Q0=0.851 5 (1+38.46I)× (18) (19) 在多孔管的L、D、I和η等参数为已知时,依据式(18)和式(19)可分别计算多孔管的总出流量和平均单孔出流量。 为了检验式(18)和式(19)的可靠性和精确性,笔者收集了新疆生产建设兵团节水灌溉办公室的试验资料,结合本人的室内模型实验数据,将实验数据和计算结果进行比对,结果如图5所示,数据点基本上分布在45°线两侧,线性回归计算的相关系数R=0.950 5,证明二者吻合情况良好。所以说明多孔管总出流量计算公式(18)和平均单孔出流量计算式(19)可用于指导实际工程的设计计算。 图5 流量折减系数ψ的对比图Fig.5 The comparison of discharge discount rate ψ (1)通过对比简单管道自由出流和沿程多孔口出流管道的流量计算公式可知,多孔管的有效水头减少了p0/γ,因此,在管材、管径、管道布置和作用水头相同的情况下,多孔管的总出流量一定小于简单管道自由出流的流量。 (2)在管材、管径、管道布置和作用水头相同的条件下,沿程多孔泄流管道的总出流量可用自由出流管道的流量乘流量折减系数计算: 多孔管平均单孔出流量的计算公式则可表示为: (3)多孔管流量折减系数主要与开孔率、长径比、管道坡度等因素有关,结合量纲分析和实验数据结果,拟合了多孔管流量折减系数ψ的计算式。 (4)得到了沿程多孔泄流管道的总出流量和平均单孔出流量计算公式,利用新疆生产建设兵团节水灌溉办室和笔者的试验资料对其进行验证,结果表明公式计算结果与试验结果相当吻合,此公式可为工程实际设计提供计算依据。 □ [1] J Barragan, I-pai Wu. Simple pressure parameters for microirrigation design[J].Biosystems Engineering,2005,90(4):463-475. [2] V Ravikumar, C R Rangathan, S Santhana Bosu. Analytical equation for variation of discharge in drip irrigation laterals[J]. Journal of Irrigation and Drainage Engineering,2003,129(4):295-298. [3] I-pai Wu,R Yue. Drip lateral design using energy gradint line approach[J]. Trans.ASAE,1993,36(2):389-394. [4] Hathoot H M. Analysis and design of trickle-irrigation laterals[J].Journal of Irrigation and Drainage Engineering,1993,119(5):756-767. [5] Hathoot H M, Hussein M. Analysis and design of sprinkler irrigation laterals[J] .Journal of Irrigation and Drainage Engineering,1994,120(3):534-549. [6] Yaohu Kang,Soichi Nishiyama. Analysis of microirrigation systems using a lateral discharge equation[J] .Transactions of the ASAE,1996,39(3):921-929. [7] Junye Wang,Zengliang Gao,Guohui Gan, et al.Analytical solution of flow coefficient for a uniformly distribute porous channel[J] . Chemical Engineering Journal,2001,(84):1-6. [8] 张国祥. 微灌毛管水力学研究:微灌水力设计计算方法探讨之一[J]. 喷灌技术,1990,(2) :9-16. [9] 郑耀泉.微灌系统水力学研究现状[J].北京农业工程大学学报,1992,12(3):26-32. [10] 张国祥.考虑三偏差因素的滴灌系统流量总偏差率[J]. 农业工程学报,2006,22(11) :27-29. [11] 张国祥,吴普特.滴灌系统滴头设计水头的取值依据[J].农业工程学报,2005,21(9):20-22. [12] Wang J Y,Ge X L,Li H L,Wu D D.Flow characteristics of multiple-hole pipe for turbine condenger—uniform flow distribution[C]∥ Proceedings of CSPE-JSME-ASME International Conference on Power Engineering,Vol.2,Shanghai,China, May 22-26,1995:754-758. [13] 刘焕芳,孙海燕,苏 萍,等.微灌自压软管合理铺设长度的确定[J] .农业工程学报,2005,21(2):46-50. [14] 魏秀菊,李 云.微灌系统沿毛管灌水器平均流量的计算[J] .农业工程学报,1994,10(9):128-133. [15] 范永申,仵 峰,宰松梅,等.新型微压滴灌灌水器水力性能试验研究[J].灌溉排水学报,2006,25(5):39-41. [16] 仵 峰,范永申,李金山,等. 低压条件下灌水器水力性能试验研究[J]. 节水灌溉,2003,(1):14-16. [17] 吕宏兴. 水力学[M]. 北京:中国农业出版社,2002:130-151.2 流量折减系数的确定
2.1 量纲分析
2.2 流量折减系数的影响因素


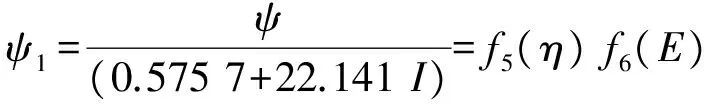


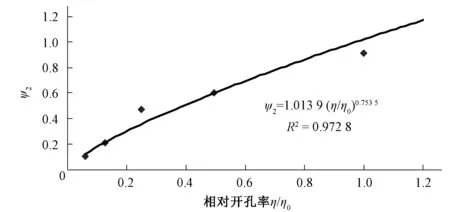


3 计算公式的实验验证

4 结 论

