流固耦合作用对双向流道泵装置流场影响

孟 凡，李彦军，邵 勇，裴 吉，陈 佳

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013；2. 江苏省太湖治理工程建设管理局, 江苏 无锡 214000)

0 引 言

双向进水流道泵站由于结构紧凑，占地省等优点，广泛应用于我国排涝灌溉领域中。但是双向进水流道泵站运行时，总是一端进水，另一端封闭，封闭端形成一个死水区。死水区的水平和垂直方向往往都有回流产生，有时还在水泵喇叭口下诱发涡带[1]，容易使机组及叶轮等产生振动而造成严重后果。对双流道泵站采用流固耦合的方法可以有效分析由于叶轮振动对泵装置内部流场造成的影响。

在流体机械领域，流固耦合方法首先应用于水轮机，研究主要集中于对水轮机转轮进行振动特性分析[2-5]。由于现代泵逐渐向大型化发展，不少学者也开始采用流固耦合的方法进行分析研究。施卫东等[6]对轴流泵内部流场和叶轮结构响应进行双向顺序流固耦合联合求解从而得到轴流泵叶片的应力及变形情况。袁寿其[7]及裴吉[8]等应用CFX和有限元软件ANSYS Workbench对螺旋离心泵进行了考虑内部流场和结构相互作用的两场交替联合求解，并以相同的设置对不考虑流固耦合作用的内部流场进行了计算，将两种计算结果进行了对比。Benra[9]等人采用双向流固耦合计算对离心泵转子和流场进行计算，并将模拟数据与实验数据进行了对比分析。

目前，对泵装置主要采用非定常数值计算与实验研究的方法[10，11]，很少采用流固耦合的方法。双流道泵装置运行时，由于双向进水流道会导致叶轮产生不同程度的振动，从而导致泵装置水力性能降低。所以对泵装置仅采用非定常计算，无法准确预估泵装置扬程，效率等外特性以及内部流场分布，从而无法给实际双向流道泵装置的建造和优化设计提供准确参考信息。

本文首次采用双向同步求解的方法，以双向轴流泵装置为研究对象，在考虑双向进出水流道的情况下，对轴流泵内流场和叶轮结构响应进行联合求解，研究了流固耦合计算前后泵装置扬程和内部流场的变化，对今后的泵站水力性能预测和优化设计具有借鉴意义。

1 基本参数与网格划分

以某大型双向流道泵站为研究对象，该泵站由于设计不当在运行过程中，会产生一定的水力振动。以下对该泵站的模型泵装置进行流固耦合内流场分析。

泵装置模型主要由叶轮、导叶、双向进水流道和双向出水流道组成。叶轮叶片数为3，导叶叶片数为5。设计参数为：流量Q=1 425 m3/h,转速n=1 550 r/min，扬程H=2.76 m。利用PROE进行三维造型，如图1所示。

图1 双流道泵站3维造型图Fig.1 3D model of pump station with two-way passage

水体域包括叶轮，导叶以及双向进出水流道；叶轮和导叶水体采用结构网格划分，进出水流道采用非结构网格划分，如图2(a)所示。结构域只考虑叶轮部分，对叶轮采用ANSYS自动网格划分功能，如图2(b)所示。流体域网格单元总数为4 030 944，固体域网格单元数为18 540。

图2 流体域与结构域网格Fig.2 Mesh of fluid and structure

2 数值计算

2.1 固体域设置

首先给定模型泵叶轮结构的材料结构钢，其特性参数为：弹性模量E=2×1011Pa、泊松比μ=0.3、密度ρ=7 850 kg/m3。定义叶轮轮毂圆柱面为固定约束,设置叶轮叶片为流固耦合作用面。设置叶轮每3度为一个时间步，时间步长为0.000 323 s。

2.2 流体域设置

假设流体是三维不可压有黏性的，利用SSTk-ω湍流模型求解雷诺时均方程。采用多重旋转坐标系技术设置旋转域和静止域。在流体域进口采用质量流量。前池的表面设置为自由水面，忽略水面的风所引起的切应力及与大气层的热交换，自由面对速度和湍动能均采用对称平面处理。在流体域出口采用固定总压，总压设定为101 325 Pa，采用自由出流边界条件。所有固壁面设置成无滑移的光滑壁面。叶轮与静止部件的交界面设置为“Transient Rotor stator”，而静止部件的交界面设置为“None”。

对叶轮叶片与流体接触的表面设置动网格，并将相应的结构表面与流体表面进行对应，设定流体向固体传递的数据类型为Total Forces，结构影响流体区域的方式设定为Total Mesh Displacement。流体域的时间步长保持与固体域一致。

2.3 双向流固耦合计算方法

在双向流固耦合问题中，需要同时求解结构动力方程以及流体的N-S方程及连续性方程。即在轴流泵叶轮叶片的耦合面上，不仅要考虑流体压力对叶轮叶片形状的影响，同时也要考虑叶轮叶片形状发生改变后，对内部流动的影响。具体求解步骤如图3所示。

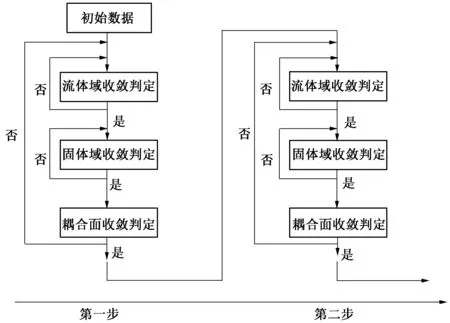
图3 双向流固耦合流程图Fig.3 Solving process of FSI two-way coupling

3 计算结果与分析

为了解内部流场随工况的变化，进行了3个工况下双向流固耦合计算。其中双向流固耦合的初始值取泵装置非定常计算10个周期后的值。

3.1 外特性分析

由于低扬程轴流泵装置实验测试误差相对较大，本文测量值为采用某实际泵装置运行时单机的扬程值，具有较高的可信度。数值计算中所采用的模型几何尺寸比实际几何尺寸缩小10倍，数值模拟中采用的模型泵转速为通过等扬程相似换算原理(1)得到，将数值模拟值与测量值进行对比。图4中，非流固耦合模拟值是指在不考虑流固耦合的情况下，泵装置的非定常计算值，流固耦合模拟值是指泵装置的双向流固耦合计算值。

(1)

式中：H，HM为实际泵扬程，模型泵扬程；D2，D2M为实际泵叶轮出口直径，模型泵叶轮出口直径；n，nM为实际泵转速，模型泵转速；ηh,ηhM为实际泵水力效率，模型泵水力效率。

根据图4可以看出，模拟值与测量值的变化趋势基本保持一致，其中非流固耦合模拟值普遍高于流固耦合模拟值和测量值，流固耦合模拟值更接近测量值。

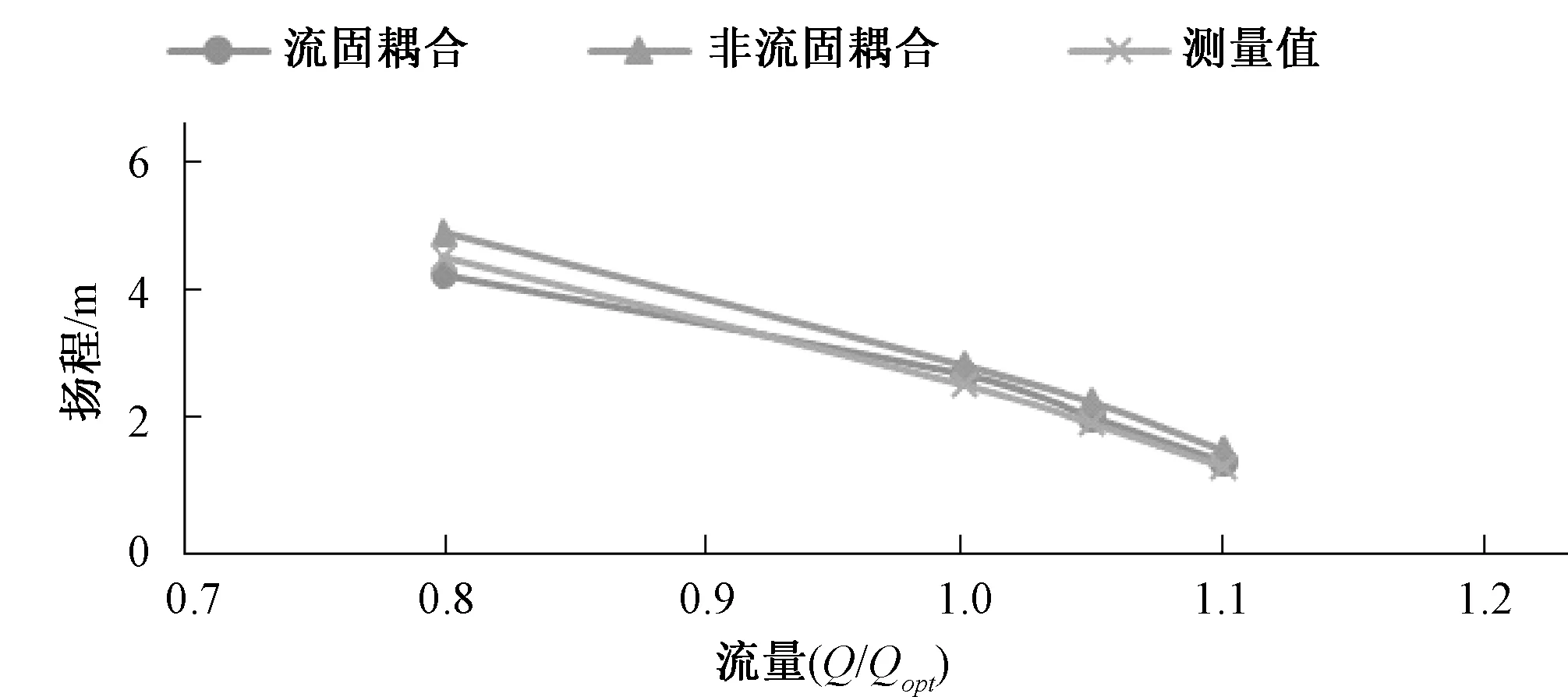
图4 泵装置扬程对比图Fig.4 Comparison of head curves

3.2 内流场分析

3.2.1 静压分布与涡量分布

由于双向进水流道容易产生涡带，使叶轮发生振动。而进水流道-叶轮干涉面上的压力分布与涡量分布可以有效反映进水流道对叶轮的影响。以最高效率点流量Q=1.0Qopt时，叶轮最后一个旋转周期内的进水流道-叶轮干涉面为研究对象。

图5(a)为不考虑流固耦合下的压力分布，图5(b)为考虑流固耦合下的压力分布，图5(c)为不考虑流固耦合下的涡量分布，图5(d)为考虑流固耦合下的涡量分布。

t为叶轮旋转时间；T为叶轮旋转一周的时间图5 流固耦合前后进水流道-叶轮干涉面静压分布与涡量分布对比Fig.5 Comparison of pressure and vorticity in the outlet of two-way inlet passage

通过图5(a)，图5(b)可以看出，无论是否考虑流固耦合，高压区主要在叶轮叶片附近，干涉面内的压力随着叶轮旋转不断呈现周期性变化，从而产生周期性的压力脉动，这也是进水流道导致叶轮发生振动的主要原因。将流固耦合前后的压力分布进行对比可以发现，考虑流固耦合下的整体压力数值更大。

通过比较图5(c)，图5(d)可以看出，无论是否考虑流固耦合，进水流道-叶轮干涉面上的涡量强度随叶轮旋转发生剧烈变化，这表明双向进水流道会对叶轮产生显著影响。将流固耦合前后的涡量强度对比后可以发现，不考虑流固耦合下的涡量强度明显小于考虑流固耦合下的涡量强度。

由图5可知，叶轮流固耦合计算前后干涉面上的静压分布和涡量分布有着显著的不同。说明双向进水流道会导致叶轮产生一定的振动，这必然导致流固耦合计算前后叶轮和导叶内流场的分布有明显不同，需要对其进行研究分析。

3.2.2 叶轮和导叶内部流动

轴流泵叶轮和导叶圆周方向的截面展开后为矩形，为了分析最高效率点流量Q=1.0Qopt时，在不同时刻下叶轮与导叶截面上的流动情况，做Span=0.5的圆周截面。

如图6所示。叶轮和导叶存在相干作用，叶轮和导叶内流场随着叶轮叶片旋转不断发生变化。其中图6(a)为不考虑流固耦合的速度云图，图6(b)为考虑流固耦合的速度云图。图6(c)为不考虑流固耦合的压力云图，图6(d)为考虑流固耦合的压力云图。

在相同时刻下，通过比较6(a)、6(b)可以看出，无论是否考虑流固耦合，流场内的高速区主要分布于叶轮工作面附近，低速区主要分布于导叶背面附近，并且都随着叶轮旋转发生变化。比较流固耦合计算前后的速度分布，考虑流固耦合下的叶轮工作面附近的高速区范围较大。

在相同时刻下，通过比较6(c)、6(d)可以看出，无论是否考虑流固耦合，流场内的高压区主要分布于叶轮背面附近，低压区主要分布在叶轮工作面，并且随着叶轮旋转发生变化。比较流固耦合计算前后的速度分布，考虑流固耦合下的叶轮背面附近的高压区范围较大，此外，可以看出叶轮-导叶交界面处的压力梯度远远大于其余地区，说明叶轮和导叶之间存在强烈的干涉作用。

t为叶轮旋转时间；T为叶轮旋转一周的时间图6 流固耦合前后叶轮和导叶内速度分布与压力分布对比Fig.6 Comparison of pressure and vorticity in the outlet of impeller

由于叶轮振动，所以流固耦合前后叶轮与导叶内流场是不一样的，这直接导致流固耦合前后叶轮叶片表面的压力分布也是不一样的。而叶轮表面的载荷直接影响到叶轮的做功效率与泵站的外特性性能，需要对其进行研究分析。

3.3 叶片表面截线压力分布

轴流泵叶片沿圆周方向的截面为机翼翼型，为了分析叶轮叶片截面上载荷随流线方向变化的情况，沿轮毂到轮缘方向分别做3条流线，分别为Span=0.1，Span=0.5，Span=0.9。

通过计算可得，3条流线在4个不同工况下流固耦合前后载荷的分布情况。由于篇幅有限，故只列出Q=1.0Qopt时，载荷随流线方向的分布图。

如图7所示，叶轮叶片工作面压力在叶轮进水边处急剧下降，叶轮叶片背面压力 在进水边处急剧上升。流固耦合前后叶片工作面载荷大小相差不大。但是流固耦合前叶片背面载荷明显小于流固耦合后叶片背面载荷，并且流固耦合前后叶片背面载荷差值随轮毂到轮缘方向逐渐减小。由此可以看出流固耦合后的叶片做功效率是小于流固耦合前的叶片做功效率。因为从轮毂到轮缘方向叶片工作面载荷和叶片背面载荷之间的差值是逐渐减小的，因此可以说明不管是否考虑流固耦合作用，叶片的做功效率随轮毂到轮缘方向逐渐降低。

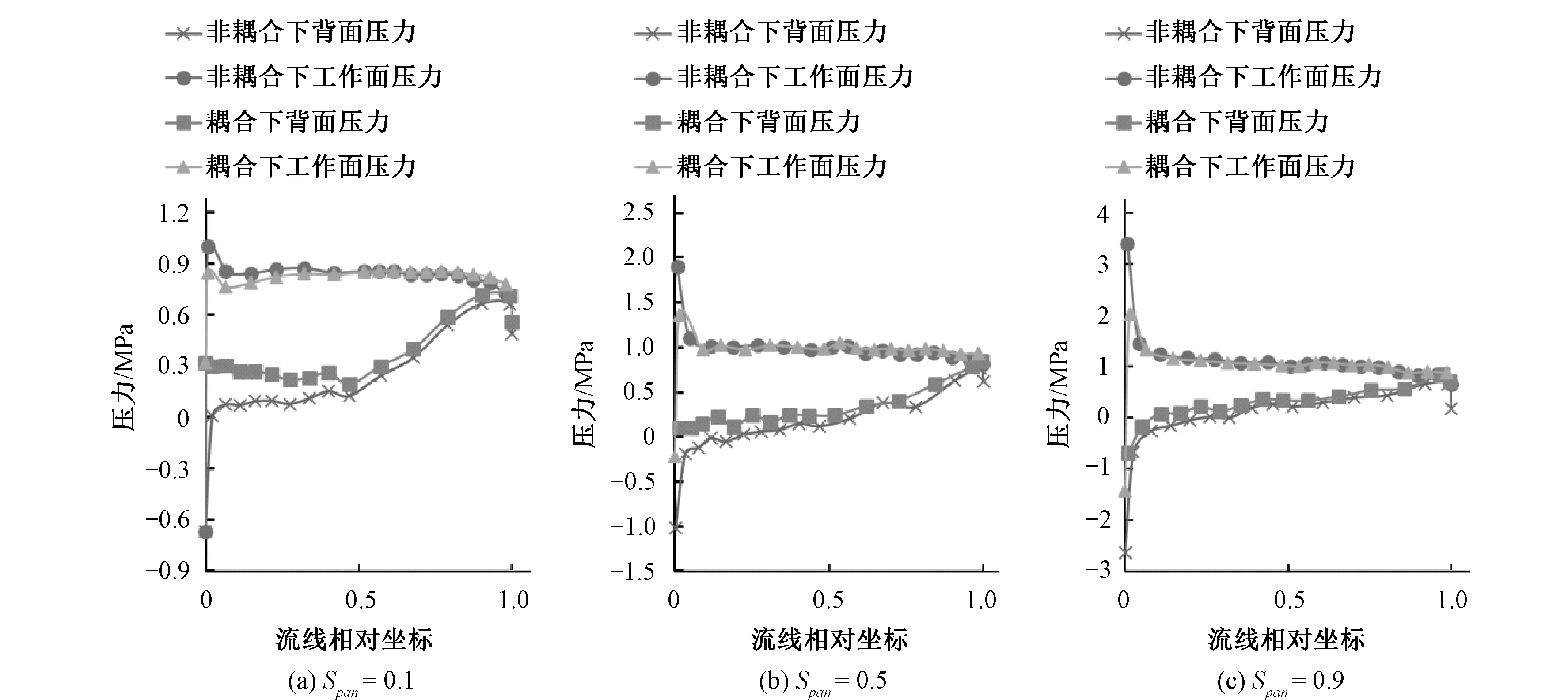
图7 流固耦合前后叶轮截线压力分布对比Fig.7 Comparison of pressure on impeller surface

4 结 论

通过对某双向流道泵装置进行双向流固耦合计算，对流固耦合作用对泵装置内部流场的影响有了进一步的认识，可以得出以下结论：

(1)在设计流量工况下，通过进水流道-叶轮干涉面上的静压分布和涡量分布可以看出，双向进水流道对叶轮和导叶内部流场有着显著影响，而流固耦合作用会使这种影响的程度增大。

(2)流固耦合作用使得叶轮和导叶内流场的速度分生改变，从而导致叶片表面的载荷发生了变化。

(3)流固耦合前后叶片工作面的载荷基本保持一致，但是考虑流固耦合下的叶片背面载荷较大。这说明流固耦合作用使得叶片做功效率降低，从而导致泵站外特性性能下降。

叶轮作为泵站中最重要的过流部件，其振动所引起的内流场变化对泵装置的性能有着非常重要的影响。所以在双向流道泵装置的计算中采用双向流固耦合计算能更加精确地对泵装置性能进行预测，对泵装置的优化设计也具有重要的指导价值。

□

[1] 傅宗甫, 严忠民, 周春天, 等. 双向进水流道模型脉动压力测试及其特性[J]. 中国农村水利水电, 2005,(1):88-91.

[2] 肖若富,朱文若,杨 魏,等. 基于双向流固耦合水轮机转轮应力特性分析[J]. 排灌机械工程学报,2013,(10):862-866.

[3] 谷朝红,姚熊亮,陈起富. 水轮机部件流固耦合振动特性研究[J]. 大电机技术,2001,(6):47-52.

[4] 张 亮, 何环宇, 张学伟, 等. 垂直轴水轮机单向流固耦合数值研究[J]. 华中科技大学学报:自然科学版, 2014,42(5):80-84.

[5] 方 兵, 金连根, 张仁贡, 等. 基于 Ansys-CFX 的混流式水轮机转轮双向流固耦合数值模拟方法[J]. 水电站机电技术, 2015,38(6):1-3.

[6] 施卫东,王国涛,蒋小平,等. 流固耦合作用对轴流泵内部流场影响的数值计算[J]. 流体机械,2012,(1):31-34,40.

[7] 袁寿其,徐宇平,张金凤. 流固耦合作用对螺旋离心泵流场影响的数值分析[J]. 农业机械学报, 2013,44(1):38-42.

[8] 裴 吉,袁寿其,袁建平. 流固耦合作用对离心泵内部流场影响的数值计算[J]. 农业机械学报,2009,(12):107-112.

[9] Benra F-K, Dohmen H J.Comparison of pump impeller orbit curves obtained by measurement and FSI simulation[C]∥2007 ASME Pressure Vessels and Piping Division Conference, 2007.

[10] 李彦军,颜红勤,葛 强,等. 大型低扬程泵装置优化设计与试验[J]. 农业工程学报,2010,(9):144-148.

[11] 李彦军,严登丰,袁寿其. 大型低扬程泵与泵装置特性预测[J]. 农业机械学报,2007,(10):36-40.