基于源信号相关特征的供水管网漏损流量研究

石 韬，高金良

(1.内蒙古自治区水利水电勘测设计院，呼和浩特市 010020；2.哈尔滨工业大学市政环境工程学院，哈尔滨 150090)

0 引 言

IWA水平衡分析法实际上是基于水体积的划分方法，将供水总量分为：售水量、免费供水量、账面漏水量和物理漏水量[1]。在供水管网中不是所有的出水点都被实时计量，而且物理流量与其他流量混合在供水管网中，所以难以明确某一时刻的物理漏损流量。供水管网中任意稳态工况下上述关系对流量同样适用，本文将供水总流量QZ划分为物理漏损流量QL用水流量QY，其中，物理漏损流量对应物理漏水量，用水流量对应售水量、免费供水量和账面漏水量，并得到基本关系式：QZ=QY+QL。

1 物理漏损流量与用水流量统计分布研究

1.1 理论基础

用偏度系数衡量统计数据分布的非对称程度、展示数据偏斜方向和程度，偏度系数计算如式(1)[2]。

(1)

式中：skew(x)为随机变量x的偏度系数；E(·)为数学期望运算；σ为随机变量x的标准差；T为随机变量x的数据长度。

按照式(2)，偏度系数为0时，表示数据呈对称分布；当偏度系数大于0时，数据呈右偏态；当偏度系数小于0时，数据呈左偏态；偏度系数绝对值越大，数据非对称程度越严重。

用峰度系数衡量随机变量的非高斯性程度，峰度系数计算如式(2)[3]。

(2)

式中：kurt(x)为随机变量x的峰度系数；T为随机变量x的数据长度。

峰度系数使用数据四阶累积量信息，当其等于3时，数据服从高斯分布，当其小于3时，数据服从亚高斯分布；当其大于3时，数据服从超高斯分布。

2 实例分析

选取我国两个供水管网计量分区的实测数据进行分析，对实测两个计量分区供水总流量分别等距分为13组，供水总流量频率分布直方图见图1。

图1 供水总流量频率分布直方图Fig.1 Total supplied water flow’s frequency distribution histogram

对实测两个计量分区供水总流量计算偏度系数和峰度系数，TJ计量分区偏度系数-0.44 、峰度系数1.81 ；CP计量分区偏度系数-0.49、峰度系数2.02，由系数和图1可知，对于TJ计量分区和CP计量分区：由于偏度系数均小于0，所以供水总流量均为左偏态，但是偏度系数绝对值比较小，供水总流量尚且具备一定的对称性；由于峰度系数均远小于3，所以供水总流量为亚高斯分布，并且具备很强的非高斯性。

上述两个典型计量分区供水总流量是非高斯的，但是这一结论尚不能推广至所有供水管网计量分区，不失一般性，假设，已知某一计量分区供水总流量是非高斯信号，假定该计量分区用水流量和物理漏损流量均是高斯信号，按照数学原理：高斯信号的线性组合仍然是高斯信号，由式(1)，可得该计量分区供水总流量是高斯信号，这与已知条件矛盾，故假设不成立；因此得到结论某计量分区供水总流量是非高斯信号，则该计量分区用水流量和物理漏损流量至多有一个高斯信号。

由供水总流量分布特征估计物理漏损流量的分布特征是间接方法，下面探索用在线水压数据直接分析物理漏损流量的分布特征。供水管网物理漏损流量与水头虽然具备一定不确定关系，但是总体上还是正相关趋势，并且稳定态下升压、降压过程以24 h形成一个闭合并循环下去，升压、降压幅度是相等的，所以供水管网物理漏损流量的高斯性可以用该区域在线测压点数据的高斯性大致代替。

以TJ某计量分区内的DXC测压点数据和CP某计量分区内的LB测压点数据进行分析，实测水头数据如图2，水头频率分布直方图见图3。

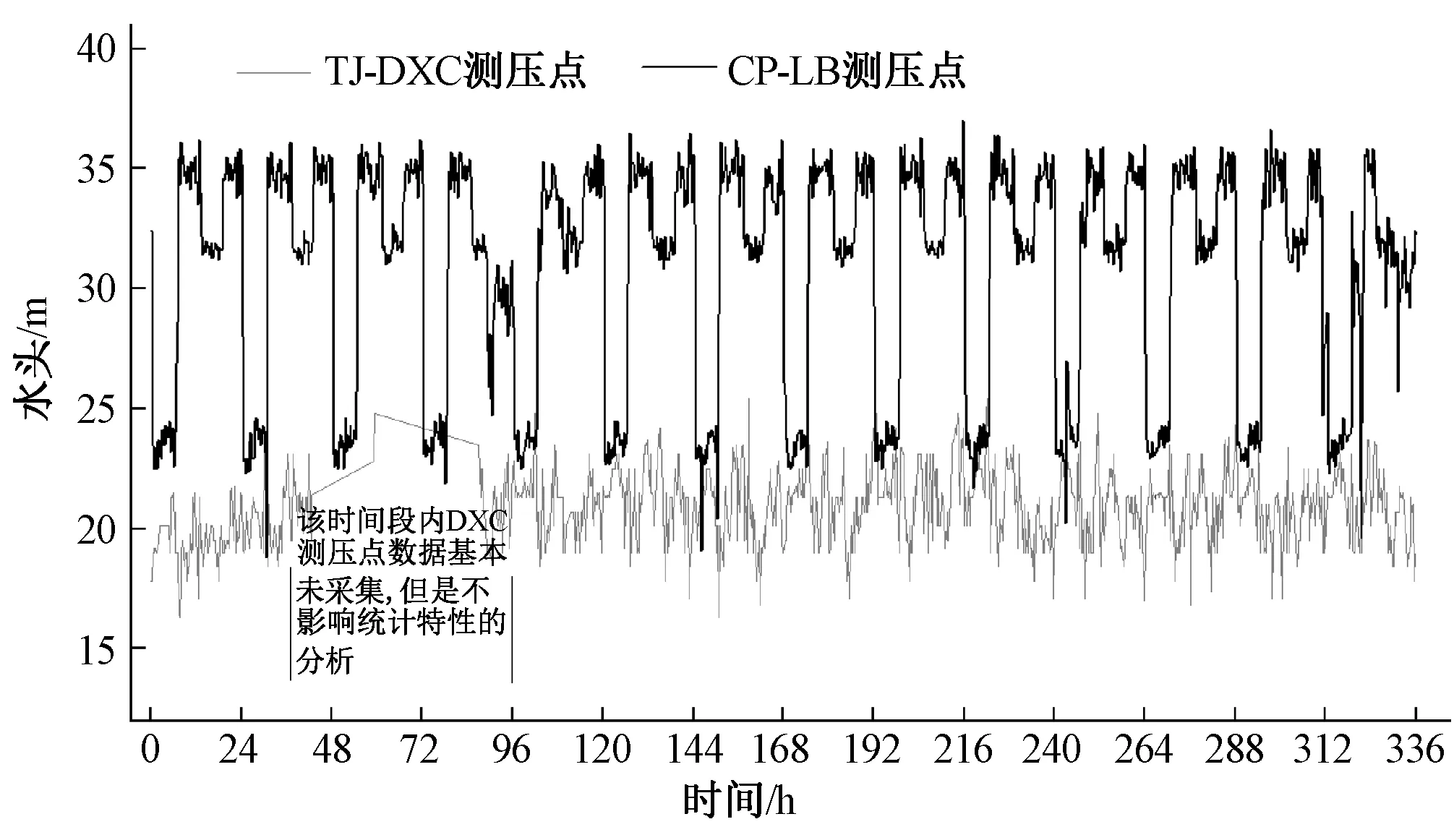
图2 测压点实测水头Fig.2 Measured data at pressure measurement points

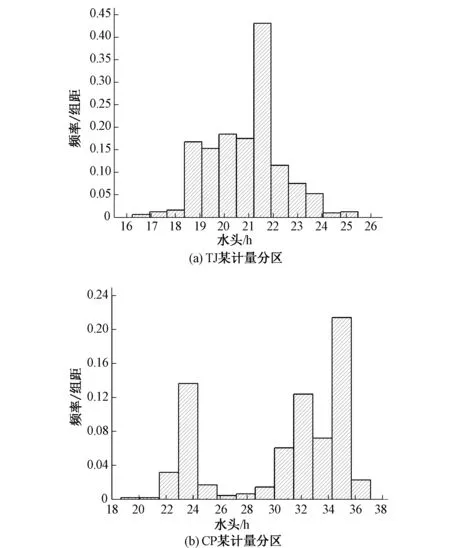
图3 水头频率分布直方图Fig.3 Pressure’s frequency distribution histogram

通过计算得到，DXC测压点水头数据的峰度系数为2.95，LB测压点水头数据的峰度系数为1.93，结合图3，得到以下结论：TJ某计量分区物理漏损流量是近乎高斯的，CP某计量分区物理漏损流量是非高斯的、是亚高斯的。

又由专业知识，计量分区的物理漏损流量是众多单漏点物理漏损流量之和，单漏点物理漏损流量可看做连续随机变量，按照中心极限定理，在一般条件下，随着独立随机变量个数的增加，其和的分布具备越来越好的高斯性，所以计量分区的物理漏损流量更有可能是高斯的，在物理漏损流量所占比重不太大的计量分区中，如果供水总流量是非高斯的，并且物理漏损流量具备较好的高斯性，那么用水流量是非高斯的，并且其高斯类别同于供水总流量高斯类别。

所以，供水管网物理漏损流量有高斯性分布趋势，但也不一定是高斯的；若供水总流量是非高斯信号，则该计量分区用水流量和物理漏损流量至多有一个高斯信号；另外，按照数学原理，当某计量分区供水总流量是高斯信号时，该计量分区用水流量和物理漏损流量也可以均为高斯信号。

2 物理漏损流量与用水流量相关性分析

物理漏损流量主要决定于管网中漏点特性、管网运行压力等因素；用水流量则明显是社会行为、用水模式所决定的，只要供水压力满足它则不会因为管网漏损水平而发生变化，在这一程度上看来，物理漏损流量与用水流量看似独立。但根据水力学规律可知，用户用水流量变化会引起管网运行水压发生变化，从而导致物理漏损流量的变化，另外，用户用水流量在满足最小服务水压的供水管网，居民用水量一定程度上受水压影响(有研究表明居民的实际用水量与水压的0.2次方呈线性关系)，漏损的发生一定程度上导致水压的降低从而改变用水流量。供水管网的物理漏损流量与用水流量间并不独立。按照数学推理可知，不独立的两个变量之间必定相关，所以供水管网的物理漏损流量与用水流量间是相关的。

3 模型机理及算法选择

在众多理论比较后，本文选择盲源分离理论和滤波理论作为建模的机理。基于以上两种理论的算法均不少于几十种(如：ICA算法中的FastICA、Informax、CICA、优化ICA等；SCA；NMF；Kalman滤波算法等等)，不同算法对于问题的基本假设、适用条件、输入参数、目标函数与约束条件、求解算法等有很大差异。两种理论在供水管网物理漏损流量分析模型中的应用既有相同之处又存在差异，在各自的算法中，相同之处在于目的都是实现物理漏损流量序列的估计，差异在于求解过程所利用的源信号信息不同，盲源分离侧重于不同源信号之间的相互信息，而滤波理论基于被提取信号本身较为准确的统计特性。因此，两种理论在各自成熟的算法中，盲源分离要求源信号至多有一个高斯信号，而滤波算法要求被提取信号尽可能的是高斯信号。通过上文对源信号的统计分布特征考虑，盲源分离和滤波理论在供水管网物理漏损流量分析模型中均有各自使用前提，二者之间相互补充。对于上文中两个源信号之间的相关关系是并不独立的，且相互制约。但盲源分离理论中传统成熟的算法要求源信号之间相互独立，由于本文分析得出用水流量与物流漏损流量存在相关关系，FastICA算法和Kalman滤波算法用于分析供水管网物理漏损流量适用性能较好，但都有不足之处，FastICA算法在于源信号不满足独立性要求；Kalman滤波算法在于供水管网物理漏损流量满足确定功率谱的程度未知，提取的信号可能存在较大误差。为此，要满足理论上的可用性，需要通过一定方法去除源信号间的相关性。

4 物理漏损流量分离及效果

在供水管网系统中，漏失量是供水总量与用水量的差值，漏失量由表观漏失和物理漏失(实际漏损)组成。实际工程中供水形式单水源或多水源环状管网居多，因此本文以实验室为基础，进行漏损量化计算。

分析图4知，单水源环状管网多漏损点盲源分离用水量与实际用水量趋势和盲源分离漏损量与实际漏损量趋势基本一致，盲源分离漏损量相对误差在2.98%到15.42%之间；将盲源分离用水量和盲源分离漏损量之和作为盲源分离总供水量，经计算分析盲源分离总供水量为6 634.75 L，盲源分离漏损量为2 676.54 L，与实际总供水量的相对误差为2.74%，盲源分离漏损率为40.34%，与实际漏损率相差1.12%。单水源环状管网多漏损点盲源分离得到的用水量和漏损量相对误差有的达到15%以上，但是盲源分离得到的总水量和实际总水量误差相对较小，本研究认为盲源分离效果可靠。

图4 用水量和漏损量趋势及漏损量相对误差图Fig.4 The trend of water consumption and leakage and leakage relative error

分析图5可知，多水源环状管网多漏损点盲源分离用水量

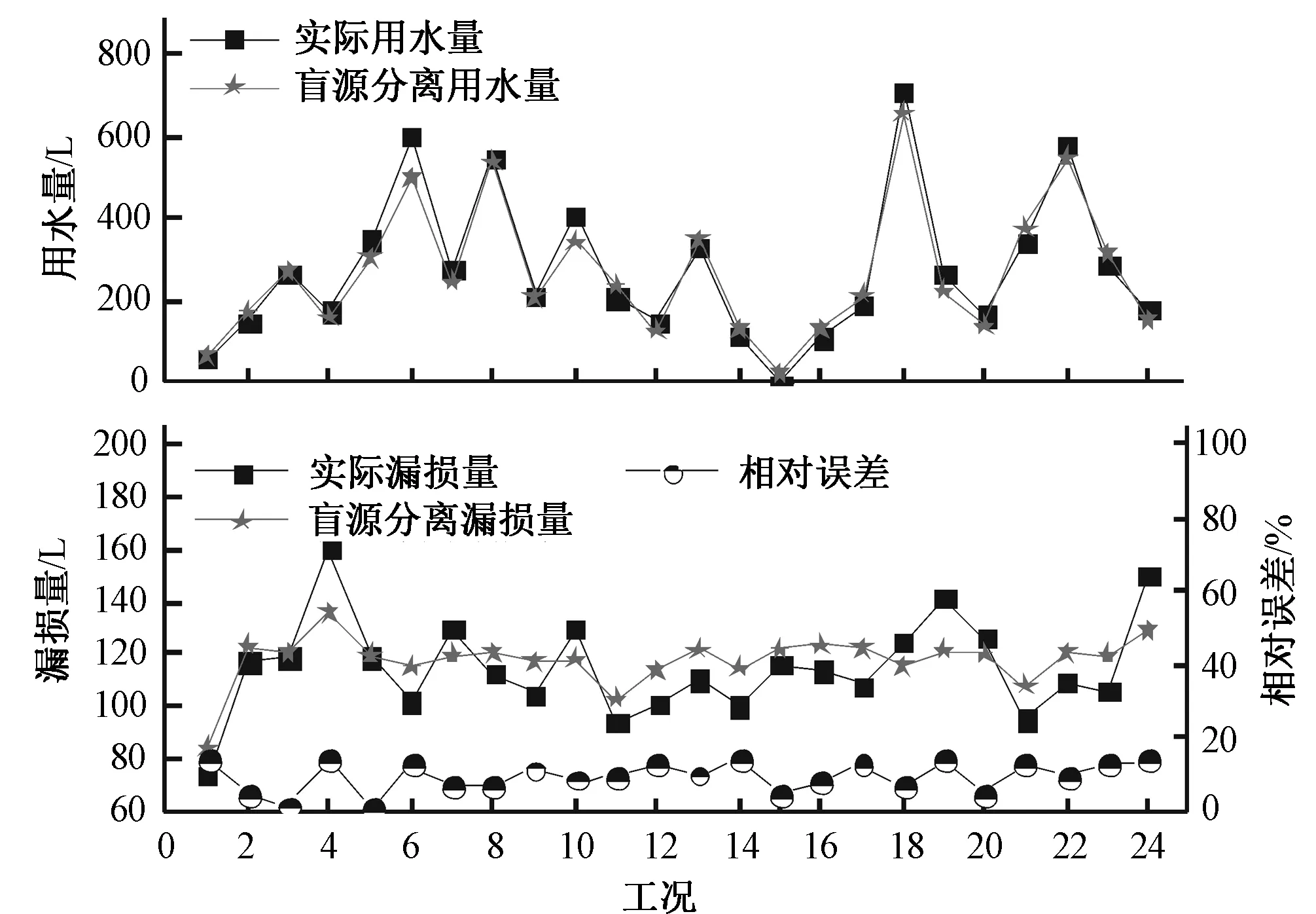
图5 用水量和漏损量趋势及漏损量相对误差图Fig.5 The trend of water consumption and leakage and leakage relative error

与实际用水量趋势及盲源分离漏损量与实际漏损量趋势基本一致，漏损量相对误差在0.69%到15.04%之间；将盲源分离用水量和盲源分离漏损量之和作为盲源分离总供水量，经计算分析盲源分离总供水量为9 340.19 L，盲源分离总漏损量为2 902.84 L，与实际总供水量的相对误差为1.89%，盲源分离漏损率为31.08%，与实际漏损率相差1.42%。本研究认为盲源分离效果较好。

5 结 语

本文通过对物理漏损流量和用水流量两个源信号高斯性及相关性分析，确定了盲源分离理论和滤波理论作为建模的机理，从众多盲源分离理论对应多种不同算法中，选择适用的算法，与Kalman滤波算法结合，能将供水管网中物理漏损流量很好分离。因此，可根据城镇供水管网实际情况，得知物理漏损流量和用水流量高斯性和相关性后，可准确选择最适用的算法对物理漏损流量进行分离。只要供水总流量具备非高斯性，建模机理就可以选择盲源分离理论，当且仅当供水总流量具备高斯性并且管网入口附近水头具备高斯性时滤波理论才是较优选择。

□

[1] Almandoz J,Cabrera E, ArreguiI F，et al. Leakage assessment through water distribution network simulation[J]. Journal of Resources Planning and Management，2005，131(6):458-466.

[2] 温利民，邹思思，吕凤虎. 偏度系数与峰度系数的信度估计[J].统计与决策，2015,(3):24-25.

[3] 于先川，胡 丹.盲源分离理论与应用[M].北京:科技出版社，2011:2-90.