基于贝叶斯模型平均的水文模型不确定性及集合模拟

江善虎，任立良，刘淑雅，袁 飞 ，杨肖丽

(1 河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2 河海大学水文水资源学院，南京 210098)

水文模型是对自然界复杂水循环过程的近似描述，是水文科学研究的重要手段和方法[1]。自1932年Sherman提出著名的水文单位线概念和1933年Horton提出著名的下渗定理至今，各国水文工作者在水文循环规律和水文过程模拟方面做了大量研究工作，获得了丰硕的成果；特别是20世纪70年代以来，国内外水文学者研制了大量不同的水文模型，并在现代洪水预报、气候变化与人类活动的水文响应、流域生态水文过程模拟和水资源规划与管理等领域广泛应用[2,3]。然而水文过程是一种受气候、气象、地形、地貌和下垫面等较多因素影响的复杂过程，蕴含着确定性的动态规律和不确定性的统计规律[4]。由于当前人类认知水平的有限，使得对水文过程的认识存在着一定的不完全性，而据此建立的水文模型也存在着诸多不确定性[5]。现阶段，根据水文模型进行流域水文过程模拟及预报时不可避免地存在着模型输入、模型参数和模型结构的不确定性[6-11]。针对模型输入(主要针对降水)的不确定性， Kavetski等[7]、Ajami等[8]引入一个服从正态分布的随机乘子来定量考虑。水文模型参数的估计方法可分为两类：第一类估计方法认为在给定流域和模型结构时，水文模型存在唯一的一组最优参数解；第二类估计方法认为在给定流域和模型结构时，水文模型的参数是一组随机变量，它们服从一个确定的联合概率分布[6, 9]。目前，已有大量的水文模型参数优化和不确定性分析方法，其中具有代表性的有第一类的遗传算法(GA)、SCE-UA算法等和第二类的基于贝叶斯统计理论的GLUE方法、SCEM-UA算法等。对于模型结构的不确定性，由于不同模型具有不同的优缺点，单一模型的模拟效果总是有限的，需充分发挥每个模型的优势，对每个模型分别考虑参数和输入的不确定性，进而对不同模型的模拟结果进行集合来消减模型结构的不确定性[10-13]。因此，综合考虑模型输入、模型参数和模型结构的不确定性，进行基于多模型的流域水文过程集合模拟，在给定确定模拟值的同时，又提供概率预报区间，是当前减少水文模拟不确定性的有效方法[14-16]。

本文选用基于子流域的新安江模型 (XAJ)[17]、混合产流模型 (HYB)[18]和改进的HYMOD模型 (HYM)[19]，从模型参数估计的两类方法出发，分别采用单纯多边形进化算法(SCE-UA)[20]和SCEM-UA算法[21]来进行模型参数优化和不确定性分析，探讨两类方法对水文模型模拟结果的影响；同时引入输入误差乘子来进行模型输入的不确定性分析；最终采用贝叶斯模型平均(BMA)将3个模型的模拟结果集合进行概率预报。

1 研究方法

1.1 水文模型

选用基于子流域的新安江模型、混合产流模型和改进的HYMOD模型进行水文过程模拟。产流机制方面，新安江模型和HYMOD模型为蓄满产流，混合产流模型考虑了蓄满和超渗两种产流机制的垂向组合。蒸散发计算，新安江模型和混合产流模型均考虑三层蒸散发，HYMOD模型仅考虑一层蒸散发。径流划分方面混合产流模型和HYMOD模型为二水源模型，新安江模型为三水源模型。汇流方面，把全流域划分为15个单元子流域，坡面汇流采用线性水库进行计算，河道汇流采用马斯京根分段连续演算方法。新安江模型有16个参数，混合产流模型为14个参数，改进的HYMOD模型有8个参数。3个模型中，HYMOD模型最为简单，混合产流模型为在新安江模型基础上改进而来，产流机制方面较新安江模型更为复杂；模型参数方面，新安江模型和混合产流模型参数相当，HYMOD模型参数最少。3个模型的驱动数据都较为简单，仅为降水和蒸发。表1列出了这3个模型的主要特征。

表1 3个水文模型主要特征比较Tab.1 The main characteristics of the three hydrological models

1.2 输入不确定性

水文模型的输入数据是水文气象要素，其中最重要的是降雨，其不确定性对水文过程模拟结果具有至关重要的影响。本研究采用一个误差乘子来定量表述降雨输入的不确定性。假定降水输入误差服从正态分布，用随机乘数来修正实测降水量，每个实测降水量都对应一个乘数：

(1)

(2)

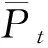
1.3 参数不确定性

采用SCE-UA算法和SCEM-UA算法来进行模型的参数优化和不确定性分析。SCE-UA是一种全局优化算法，该算法结合了现有算法(包括基因算法等)的一些优点，将基于确定性的复合型搜索技术和自然界中的生物竞争进化原理相结合，可以解决高维参数的全局优化问题，且不需要显示目标函数或目标函数的偏导数[19]。SCE-UA算法可以有效、快速地搜索到水文模型参数的全局最优解，在水文模型参数优化中得到了广泛的应用。SCEM-UA算法是Vrugt等于2003年对单纯多边形进化算法(SCE-UA)加以改进而提出的一种全局搜索算法，该算法不仅能搜索到一套具有最大似然性的参数组，同时也能估计参数不确定性[21]。SCEM-UA算法结合了马尔科夫蒙特卡洛(MCMC)采样技术，以Metropolis-Hastings算法(简称M-H算法)取代SCE-UA算法中的坡降算法，并估计出最优参数组及其后验概率分布[22]。

1.4 贝叶斯模型平均

BMA是一种基于贝叶斯理论的多模型集合分析方法，它基于似然函数推断单个模型的权重，保证模拟效果更好的模型具有更高的权重系数；通过多个水文模型竞争，BMA可产生更可靠的集合预报值。BMA不仅可以用于模型集合，而且可以用于计算单个模型和模型集合的不确定性。其基本原理简介如下。

假设y为BMA集合预报流量，D=[X,Y]为实测数据(其中X表示输入资料，Y表示实测的流量资料)，f=[f1,f2,…,fk]为k个模型预报的集合。BMA的概率预报表示如下：

(3)

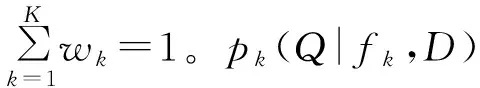
(4)

(5)

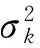
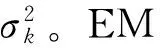
1.5 不确定性区间估算

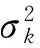
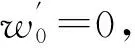
(3) 重复步骤(1)和(2)M次。M是在任意时刻t的样本容量，本文中令M=1 000。将它们从小到大排序，BMA的95%预报区间就是2.5%和97.5%分位数之间的部分。

针对SCEM-UA算法优化模型的模拟结果，将模型参数收敛前的模拟结果和收敛后的模拟结果综合起来考虑，因为样本容量足够大(本文为15 000组)，可以近似服从正态分布，根据正态总体均值的区间估计方法可计算出95%置信水平下样本的置信区间[8]。

1.6 评估指标

采用Nash-Sutcliffe效率系数(NS)、偏差(bias,B)和均方根误差(Root mean square error,RM)来评价模型模拟径流的精度。其中NS系数表征模拟径流和观测径流的吻合程度；B反映模拟径流的系统偏差程度；RM表征模拟径流和观测径流的误差大小。采用覆盖率(Containing ratio,CR)、平均带宽(Average Bandwidth,BW)和平均偏移度(Average Deviation Amplitude,DA)来评价模型预报区间的准确度[23]。CR指预报区间覆盖实测流量数据的比例，CR越大，表示预报区间的覆盖率越高。BW表示预报区间的平均带宽，对于一定的置信水平，在保证有较高的覆盖率前提下，BW越窄越好。DA反映预报区间的中心线偏离实测流量过程线的程度，理论上DA越小，表示预报区间的对称性越好。

2 研究数据

2.1 研究区域概况

洣水流域地处湖南省的东南部(东经112°52′～113°56′ ，北纬26°01′～27°10′)，为湘江的一级支流，其中甘溪水文站以上控制面积为9 977 km2(图1)。流域地势东南高、西北低，海拔高程自东南向西北由2 093 m降低到49 m，平均坡降为1.01‰。流域气候类型属亚热带季风型湿润性，四季分明，降水充沛，多年平均年降水量达1 561.0 mm。流域多年平均气温18.0 ℃，多年平均风速1.8 m/s。

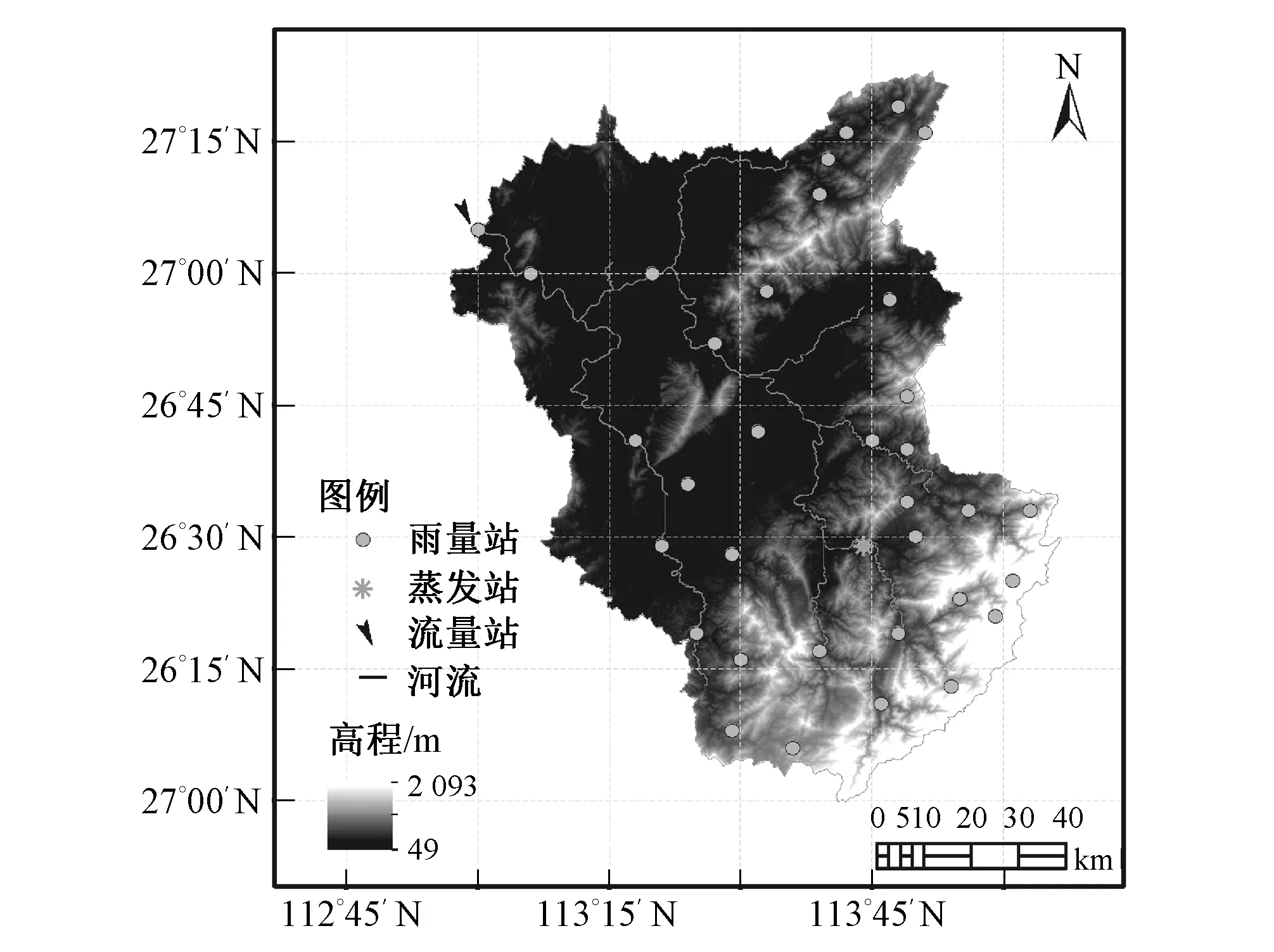
图1 洣水流域地理位置及测站分布图Fig.1 Location of Mishui basin and distribution of measurement stations

2.2 研究数据

收集洣水流域35个雨量站、1个蒸发站(五里牌，E601蒸发皿)和1个流量站(甘溪水文站)2000-2008年逐日降雨、潜在蒸发和流量观测数据。采用临近三站点反距离加权法(IDW)将点雨量插值到流域面上分布。流域地形资料采用美国地质调查局(USGS)的全球30″数字高程模型数据(DEM)。应用ArcGIS提取构建分布式流域水文模型所需的基本空间信息，包括流域边界、栅格水流流向、各栅格至流域出口断面的河长等，并将流域划分为15个子流域。土地覆被资料采用美国马里兰大学全球1 km土地覆被资料，统计得洣水流域主要植被类型为林地占61.8%，草地占24.6%，耕地占13.3%，城乡和水体占0.3%。

3 结果对比

利用洣水流域2000-2008年连续9年的日降雨-径流资料进行水文过程模拟和不确定性分析，其中2000-2005年为模型的率定期，2006-2008年为模型的验证期。SCE-UA算法中，采用RM指标作为目标函数来衡量优选参数的优劣，反映模型模拟值和实测值之间的误差。SCEM-UA算法中，初始均匀分布样本个数为1000，复合型个数为5，判断后验分布推断完毕的样本个数为5000，最大运行次数为15000。本研究采用多种情景进行水文过程模拟和不确定性分析：① 仅考虑模型参数的不确定性，采用SCE-UA算法和SCEM-UA算法分别进行单个模型的参数优选和不确定性分析；② 引入一个误差乘子来定量表述降雨输入的不确定性，对每一模型同时考虑模型参数和模型输入的不确定性；③ 采用BMA将3个模型的模拟结果集合，综合考虑模型参数、模型输入和模型结构的不确定性。具体结果分析如下。

3.1 BMA集合和单个模型的模拟值对比

表2为单个模型只考虑模型参数不确定性，单个模型考虑模型参数和模型输入不确定性，以及利用BMA法综合考虑模型参数、模型输入和模型结构不确定性的径流模拟精度比较(NS、B、RM)。图2和3分别为BMA法集合SCE-UA优化和SCEM-UA优化的3个模型的模拟结果。从表2和图2，图3中可以看出：基于SCE-UA和SCEM-UA算法优选参数，3个模型在洣水流域都能取得较好的模拟结果，率定期模型的NS都在0.85以上，验证期模型的NS都在0.80以上；模型在率定期的模拟精度要优于验证期的模拟精度，说明模型模拟结果在验证期存在更大的不确定性。3个模型考虑输入的不确定性后，模拟精度和不考虑输入不确定时相当，没有大的提高(仅验证期新安江模型和混合产流模型的NS系数有所提高)，这可能是由于：① 洣水流域雨量站点较为密集，降水输入较为准确；② 3个模型中均存在降水蒸散发折减系数参数，在一定程度上描述了模型输入的不确定性；③ 考虑模型输入的不确定性，引入了两个新的模型参数，一定程度上增加了模型参数的不确定性。不管是SCE-UA算法，还是SCEM-UA算法，采用BMA法综合考虑模型参数、模型输入和模型结构不确定性的模拟结果都要优于单个模型，在率定期和验证期，BMA都能取得最高的NS(SCE-UA优化的模型BMA集合后，率定期NS为0.91，验证期为0.88；SCEM-UA优化的模型BMA集合后，率定期NS为0.92，验证期为0.87)、最小的B和最小的RM，尤其在验证期BMA集合的NS要较单个模型有很大提高，说明BMA集合多模型提高预报精度的有效性。

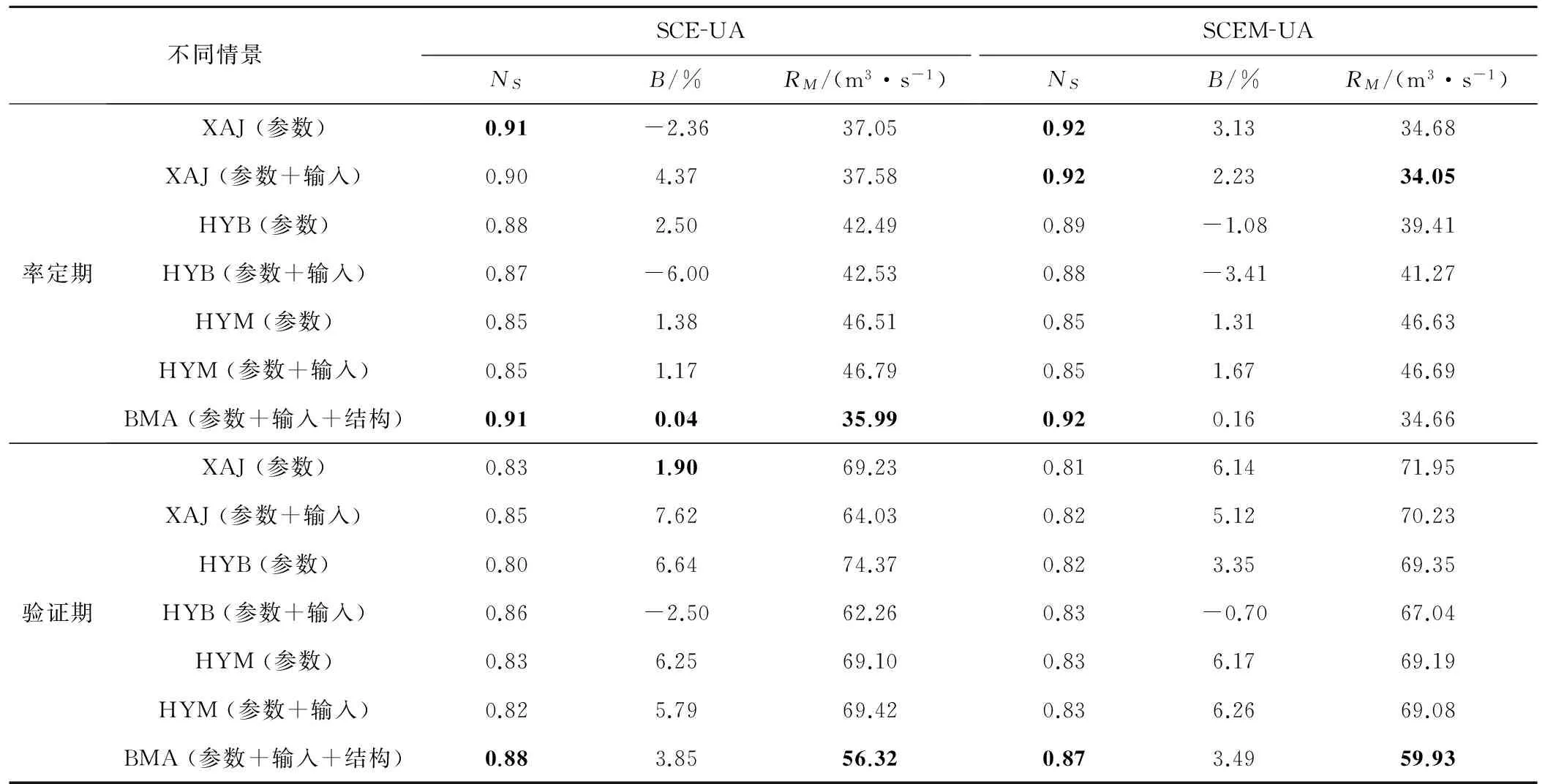
表2 不同模拟情景下SCE-UA和SCEM-UA优化的水文模型模拟精度比较Tab.2 Precision performance of the streamflow simulation series at different simulation cases

注：参数表示仅考虑参数不确定性；参数+输入表示同时考虑参数和输入不确定性；参数+输入+结构表示综合考虑模型参数、输入和结构不确定性；黑体字表示最优值。

3.2 BMA集合和单个模型的预报区间对比

表3给出了不同方案下单个模型和BMA集合模拟径流的不确定性区间优良性评价指标(CR、BW、DA)。图2和3分别展示了BMA法集合SCE-UA优化和SCEM-UA优化的3个模型模拟径流的95%置信区间。从表2和图2，图3中可以看出：不管是SCE-UA算法，还是SCEM-UA算法，采用BMA方法综合考虑模型参数、模型输入和模型结构不确定性的预报不确定性区间要优于单个模型，BMA的模拟径流不确定性区间具有更高的覆盖率和更优的平均偏移幅度，但它较单个模型具有更大的平均带宽；这与Xiong等[23]和董磊华等[10]的研究结论一致。横向比较表3中SCE-UA算法和SCEM-UA算法的模拟结果，可以发现，SCEM-UA算法的概率预报性区间具有更高的CR、更小的BW和更优的DA；其中采用BMA方法集合SCEM-UA算法优化的3个模型模拟结果，其率定期95%置信区间的CR达到95.62%，验证期95%置信区间的CR达到95.17%，几乎包含了整个实测径流序列，取得了最优的结果。总体上，采用BMA方法综合考虑模型参数、模型输入和模型结构不确定性，较单个模型能够提供更可靠的预报不确定性区间；与SCE-UA算法相比，SCEM-UA算法能更好进行参数的不确定性分析，基于SCEM-UA算法和BMA集合得到的概率预报区间更为准确，具有更大优势。

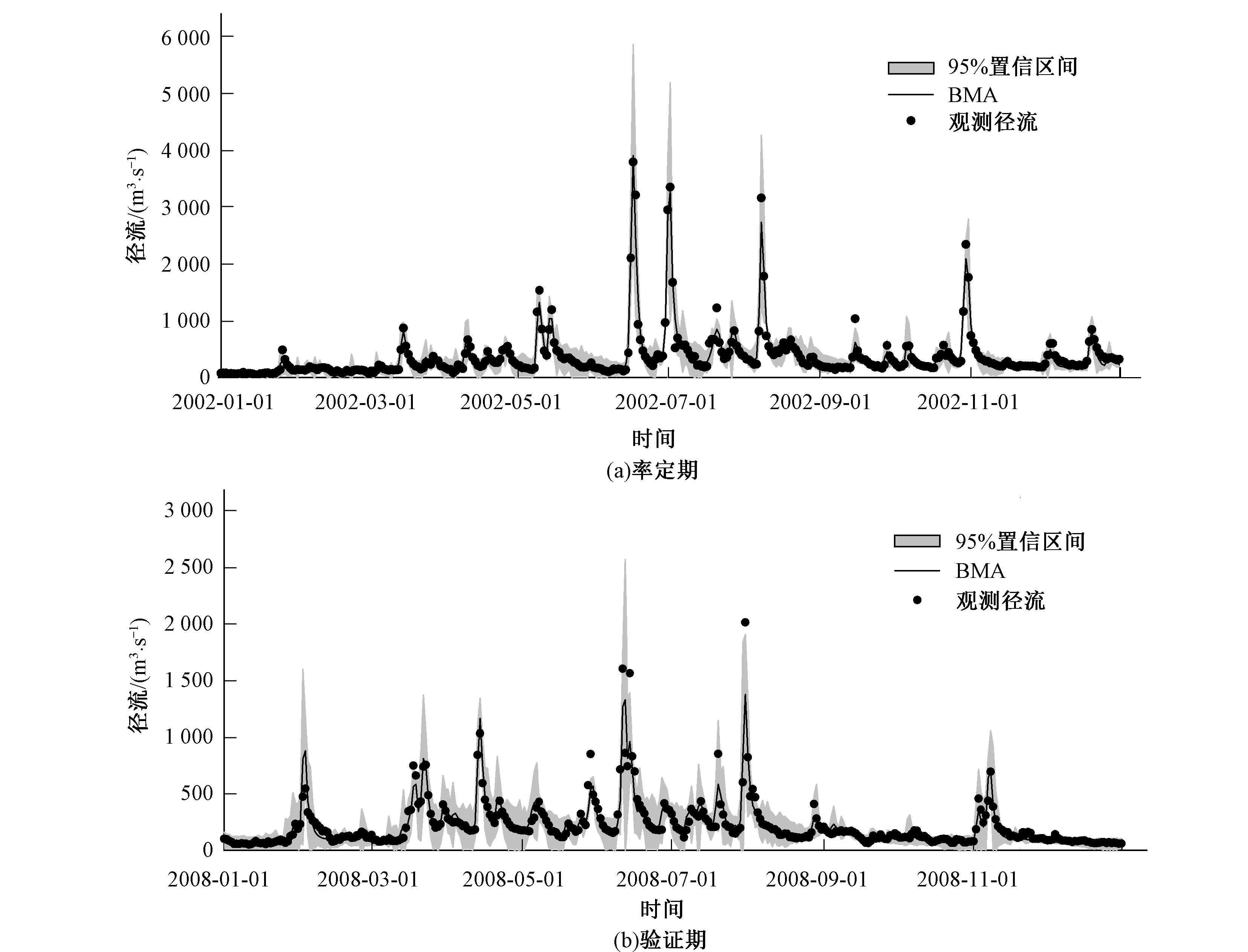
图2 贝叶斯模型平均集合SCE-UA优化的3个模型的模拟结果Fig.2 The BMA mean from the SCE-UA based simulations of the three hydrological models, and the 95% confidence interval

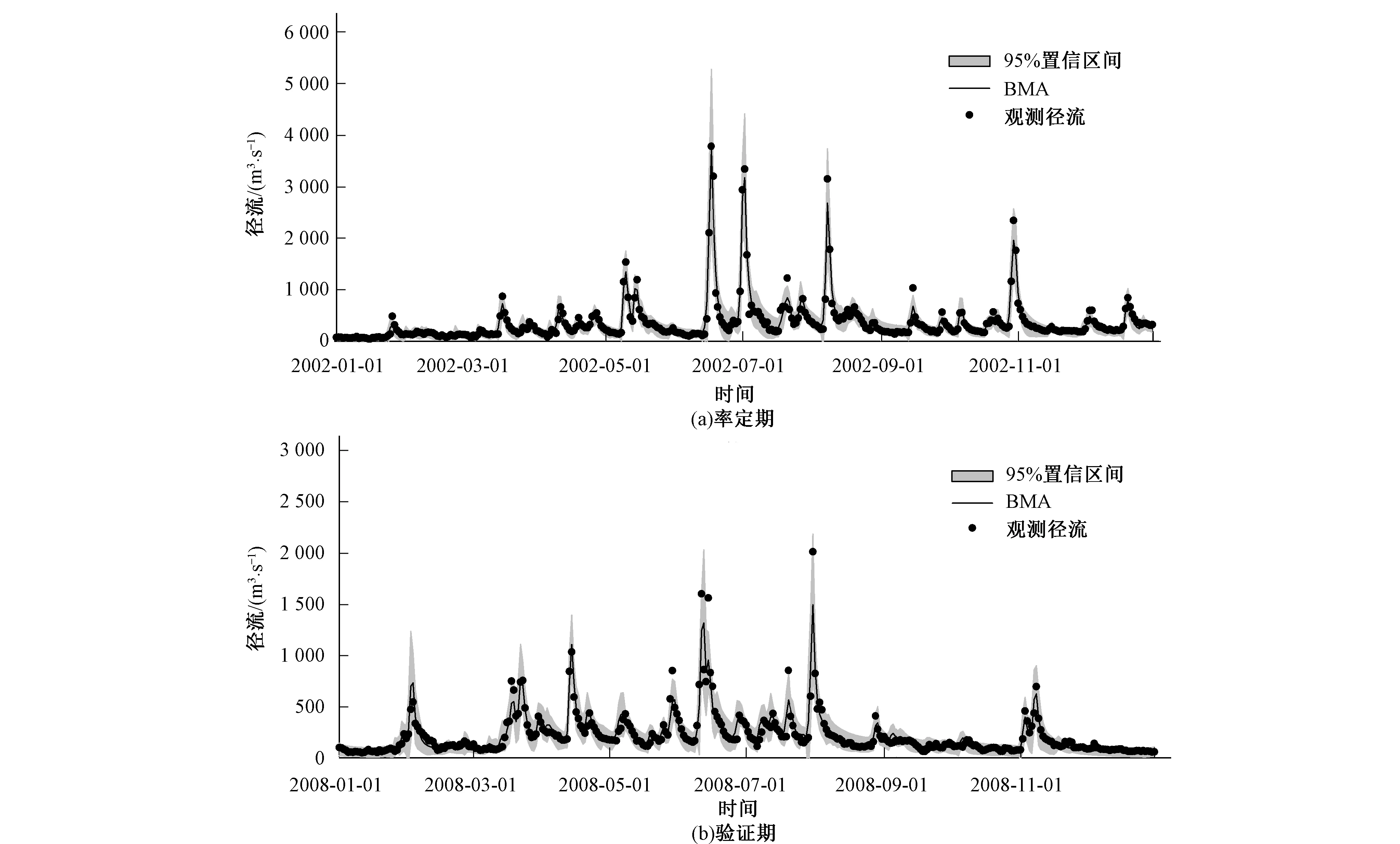
图3 贝叶斯模型平均集合SCEM-UA优化的3个模型的模拟结果Fig.3 The BMA mean from the SCEM-UA based simulations of the three hydrological models, and the 95% confidence interval

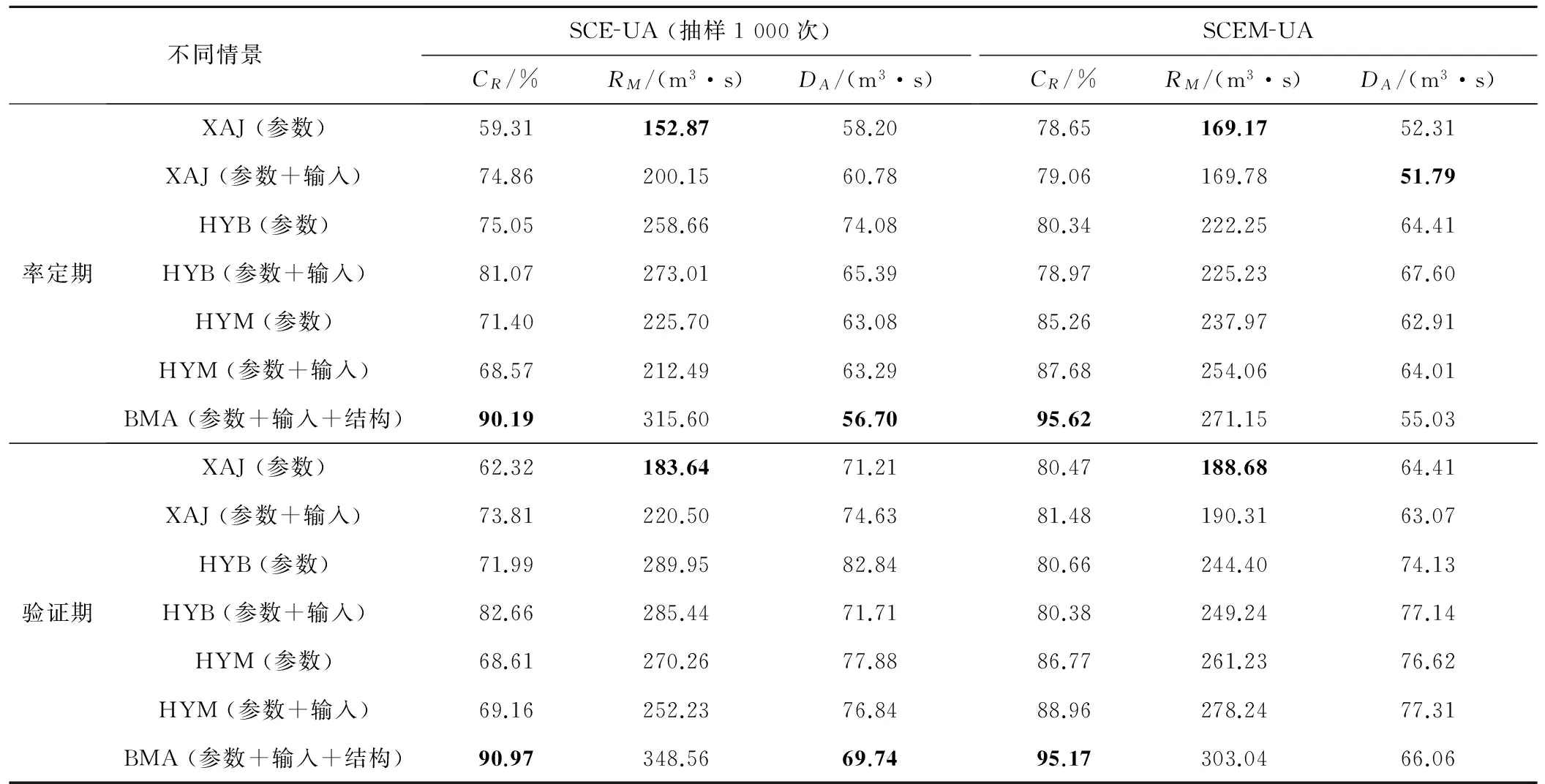
不同情景SCEUA(抽样1000次)CR/%RM/(m3·s)DA/(m3·s)SCEMUACR/%RM/(m3·s)DA/(m3·s)率定期XAJ(参数)59.31152.8758.2078.65169.1752.31XAJ(参数+输入)74.86200.1560.7879.06169.7851.79HYB(参数)75.05258.6674.0880.34222.2564.41HYB(参数+输入)81.07273.0165.3978.97225.2367.60HYM(参数)71.40225.7063.0885.26237.9762.91HYM(参数+输入)68.57212.4963.2987.68254.0664.01BMA(参数+输入+结构)90.19315.6056.7095.62271.1555.03验证期XAJ(参数)62.32183.6471.2180.47188.6864.41XAJ(参数+输入)73.81220.5074.6381.48190.3163.07HYB(参数)71.99289.9582.8480.66244.4074.13HYB(参数+输入)82.66285.4471.7180.38249.2477.14HYM(参数)68.61270.2677.8886.77261.2376.62HYM(参数+输入)69.16252.2376.8488.96278.2477.31BMA(参数+输入+结构)90.97348.5669.7495.17303.0466.06

注：参数表示仅考虑参数不确定性；参数+输入表示同时考虑参数和输入不确定性；参数+输入+结构表示综合考虑模型参数、输入和结构不确定性；黑体字表示最优值。

4 结 论

本文选用3个基于子流域的半分布式水文模型(新安江模型、混合产流模型和HYMOD模型)，采用贝叶斯模型平均法(BMA)开展水文模型不确定性及集合模拟实例研究。模拟结果表明： SCE-UA算法和SCEM-UA算法优选的参数使得3个模型都能取得较好的模拟结果，但SCEM-UA算法能给出模型参数的后验概率分布，进行参数的不确定性分析，得到模型的概率预报区间，具有更大的优势；模型在率定期的模拟结果要优于验证期的模拟结果，说明模型在验证期具有更大的不确定性；考虑模型输入的不确定性，模拟径流的精度没有较大提高，但计算的概率预报区间精度有一定的提高；采用BMA方法，综合考虑模型参数、模型输入和模型结构的不确定性，其模拟结果优于单个模型，尤其在验证期BMA集合模拟结果精度提高更大；此外，BMA集合模拟的概率预报性区间也优于单个模型，说明了BMA集合模拟对提高水文预报精度和进行不确定性分析的有效性；比较SCE-UA算法和SCEM-UA算法的BMA集合模拟结果，可以发现，基于SCEM-UA算法和BMA集合得到的概率预报区间更为准。综合而言，采用SCEM-UA算法考虑模型参数的不确定性，再利用BMA集合各模型结果，能够得到最为精确的预报值和最为可靠的概率预报区间。

□

[1] 徐宗学, 程 磊. 分布式水文模型研究与应用进展[J]. 水利学报, 2010,41(9):1 009-1 017.

[2] 徐宗学. 水文模型[M]. 北京:科学出版社, 2009.

[3] Beven K. Rainfall-Runoff modeling[M]. Chichester: Wiley, 2000.

[4] 严登华, 袁 喆, 王 浩, 等. 水文学确定性和不确定性方法及其集合研究进展[J]. 水利学报, 2013,44(1):73-82.

[5] 梁忠民, 戴 荣, 李彬权. 基于贝叶斯理论的水文不确定性分析研究进展[J]. 水科学进展, 2010,21(2):274-281.

[6] 王 浩, 李 扬, 任立良, 等. 水文模型不确定性及集合模拟总体框架[J]. 水利水电技术, 2015,46(6):21-26.

[7] Kavetski D, Kuczera G, Franks S W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resources Research, 2006,42(3).

[8] Ajami N K, Duan Q Y, Sorooshian S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction[J]. Water Resources Research, 2007,43(1).

[9] 王书功. 水文模型参数估计方法及参数估计不确定性研究[M]. 郑州: 黄河水利出版社, 2010.

[10] 董磊华, 熊立华, 万 民. 基于贝叶斯模型加权平均法的水文模型不确定性分析[J]. 水利学报, 2011,42(9):1 065-1 073.

[11] Liang Z M, Wang D, Guo Y, et al. Application of Bayesian Model Averaging Approach to Multi-model ensemble Hydrologic Forecasting[J]. Journal of Hydrologic Engineering, 2013,18(11):1 426-1 436.

[12] Deng L H, Xiong L H, Zheng Y F. Uncertainty analysis of coupling multiple hydrologic models and multiple objective functions in Han River, China[J]. Water Science and Technology, 2013,68(3):506-513.

[13] 杜新忠, 李叙勇, 王慧亮, 等. 基于贝叶斯模型平均的径流模拟及不确定性分析[J]. 水文, 2014,34(3):6-10.

[14] 任立良, 江善虎, 袁 飞, 等. 水文学方法的研究与诠释[J]. 水科学进展, 2011,22(4):586-592.

[15] 陆桂华, 吴 娟, 吴志勇. 水文集合预报试验及其研究进展[J]. 水科学进展, 2012,23(5):728-734.

[16] 袁 喆, 严登华, 杨志勇, 等. 集合建模在径流模拟和预测中的应用[J]. 水利学报, 2014,45(3):351-359.

[17] 赵人俊. 流域水文模拟-新安江模型与陕北模型[M]. 北京: 水利电力出版社, 1984.

[18] Ren L L, Zhang W, Li C H, et al. Comparision of Runoff Parameterization Schemes with Spatial Heterogenetity across Different Temporal Scales in Semihumid and Semiarid Regions[J]. Journal of Hydrologic Engineering, 2008,13(5):400-409.

[19] 宋文献, 江善虎, 杨春生, 等. SCE-UA、SCEM-UA算法对改进的HYMOD模型模拟结果的影响[J]. 水电能源科学, 2013,31(11):17-20.

[20] Duan Q, S Sorooshian, V Gupta. Effective and efficient global optimization for conceptual rainfall-runoff models[J]. Water Resources Research, 1992,28(4):1 015-1 031.

[21] Vrugt J A, H V Gupta, W Bouten, et al. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters[J]. Water Resources Research, 2003,39(8):1 201.

[22] Roberts G O, Tweedie R L. Geometric convergence and centra limit theorems for multidim ensional Hastings and Metropoli algorithms[J]. Biometrika, 1996,83(1):95-110.

[23] Xiong L H, Wan M, Wei X J, et al. Indices for assessing the prediction bounds of hydrological models and application by generalized likelihood uncertainty estimation[J]. Hydrological Science Journal, 2009,54(5):852-871.