与马斯京根汇流模型耦合的BP神经网络修正算法

王建金，石 朋,2，瞿思敏，肖紫薇，戴韵秋，陈颖冰，陈星宇

(1.河海大学 水文水资源学院，南京 210098；2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098)

水文模型是洪水预报中应用最广泛的预报方式之一，通过流域历史长期水文资料率定模型参数，而后用于实际水文预报工作中。水文现象在时间上具有极为明显的连续性和相关性，单个时刻预报的误差如若不能及时消除，势必会对未来预报的精度产生影响，长期积累的误差甚至会导致预报结果严重偏离，这时就需要应用实时修正技术[1]。

BP神经网络算法是从现代控制理论引入水文的一种智能算法，广泛应用于洪水预报、水质分类和水资源规划等水文领域[2,3]。该算法采用有导师学习的模式，要求预报的结果必须有实测的真值指导模型率定，因而在实时修正领域只能对水文预报的最终结果进行修正。传统BP神经网络修正算法基于误差自回归的预报原理[4]，预报精度与二阶AR模型类似[5]，且无法延长预见期，应用受到较大限制。

本文对BP神经网络的基本原理结合水文物理规律进行改进，解决了修正量无直接对应的实测数据指导模型率定的限制，与马斯京根汇流模型耦合，实时修正主河道各河段的区间入流，在不损失预见期的前提下，提升预报精度。选取海南省定安河流域历史洪水资料对算法的稳定性和可靠性进行检验[6]，并与二阶AR模型[7]的修正结果进行对比。

1 研究方法和模型原理

1.1 马斯京根汇流模型

马斯京根法是在1938年由G.T.麦卡锡提出的河道汇流演算模型，依据上游断面洪水过程推求下游出流，在国内外均有广泛应用实例。伴随着水文预报由集总式模型向半分布式、分布式水文模型发展的总体趋势，流域内各计算单元得到的出流结果均需要按一定原则汇入河道，马斯京根汇流模型在众多汇流算法中效果显著。流域内不同位置产流的汇流时间有较大差异，当前时刻的预报结果受上游之前时刻的河道区间入流影响较大，及时修正主河道各河段区间入流的误差对预报的准确性意义重大。

1.2 传统BP神经网络修正算法

传统BP神经网络修正算法采用有导师指导的学习模式，修正量必须有直接的实测真值指导神经网络的率定。该算法基于误差自回归的原理，输入量为预报时刻前N个时段的预报误差信息，计算得到预报时刻的误差值，计算流程如下：

et=Qp,t-Qo,t

(1)

et+L=FBP(et,et-1,…,et-N+1)

(2)

(3)

在实时修正领域，各时段间误差的自相关性在邻近时刻达到最强，故而预报精度会随着预见期的增加逐步下降，且对于模型计算过程中无实测真值的中间变量，例如各子流域计算的产流量，主河道的区间入流量等不具有修正能力。

1.3 BP神经网络耦合修正算法

本文对神经网络算法中反向传播部分进行改进，实现了与马斯京根汇流模型耦合，以流域最终出流指导主河道区间入流修正的耦合修正算法。

以流域概化后主河道有m处河段区间入流的情况为例，模型输入为控制断面实测出流和预报流量，输出为m处河段L个小时前的区间入流修正量，修正后重新计算L个小时的马斯京根演算过程即得到最终预报结果，计算流程如下：

ΔQm,t=FBPC(Qp,t+L,Qo,t+L)

(4)

(5)

BP神经网络算法通过正向计算结果和反向传播误差信息修正网络，基本原理详见文献[8]。当神经网络正向传播得到各河段计算误差ΔQm，并经由马斯京根汇流得最终计算误差ΔQp后，反向传播部分的改进方式如下：

基于马斯京根线性演算的特点，假定各河段区间入流修正量的误差与修正后演算的最终出流量的误差之间也存在线性关系，则以下关系成立：

ΔQmo-ΔQm=km(Qo-Qp)

(6)

式中：ΔQmo和ΔQm分别为第m个河段区间入流的误差的真值和计算值；Qo是实测流量；Qp是修正后的计算流量；km为汇流演算的比例系数，大小介于0和1之间。

由神经网络算法可知：

ΔQm=wk1mo(k-1)1+wk2mo(k-1)2+…+wknmo(k-1)n+θkm

(7)

式中：wkim是k-1层第i个节点对应k层第m个节点的权值；o(k-1)i是k-1层第i个节点的输出；θkm是k层第m个节点的阈值。

模型第m个河段的误差函数：

(8)

因此，神经网络最后一层由第m个河段区间入流误差导致的权值、阈值的修正公式如下：

(9)

(10)

倒数第二层由第m个河段区间入流误差导致的权值、阈值的误差修正公式如下：

(11)

ηkm(Qo-Qp)wkimo(k-1)i(1-o(k-1)i)o(k-2)j

(12)

其余各层按上式方式继续推导即可，由上述公式可知，只要确定了各河段汇流演算的修正比例系数km，该改进方案就可以达到预期的目的。km的取值提供以下3种方式：①在马斯京根汇流过程中保留每一步入流和出流的中间变量，基于数理统计的方式进行线性拟合确定；②采用马斯京根汇流系数的计算方式获得；③基于神经网络本身的学习能力采用二速收敛法：神经网络各层的修正是一个递推的模式，只需要关注最后一层的网络修正。

采用最速下降法确定误差反向传播的修正方向，然后将两种不同修正速率进行反向传播，构建km1和km2，改进的修正准则如下：

(13)

式中：ΔQp为计算流量的误差；ΔQmp为神经网络计算的第m个河段的修正量；sign(·)为符号判断函数，判断正负号。

令km1≪km2且介于0到1之间，即神经网络计算的修正量方向与模型误差方向相反时，采用km2进行大幅度的纠正，反之采用km1只进行小幅度的修正，首先达到单次修正时所有河段的修正量方向相同，然后达到修正量的大小符合要求。以上准则确保了相应权值和阈值可以在正确方向上进行修正，在大量数据反复率定的情况下，该算法最终可以很好地收敛。

2 算法验证

2.1 研究区概况

定安河流域位于海南岛中部偏东北，与乐会水流域共同构成万泉河的两大源头。地处热带季风性气候区，全年高温，年平均气温不低于22 ℃。雨量充沛，年平均降雨1 639 mm，有明显的旱季和雨季，洪涝灾害多发于5月到翌年的10月，全年降雨的70%～90%发生这一时期。全流域雨量站共计11处，流域出口处建有加报水文站，集水面积1 257 km2。该流域具有多年水文气象连续监测资料，选取共计20场次洪开展本次研究。

2.2 模型构建

定安河流域运用泰森多边形的方式共计划分为11个子流域，分别由新安江模型计算各子流域的出流结果，出流结果作为区间入流汇入主河道并应用马斯京根河段连续演算至流域出口断面。经演算，共计7个河段有区间入流汇入，需要进行实时修正。神经网络耦合修正模型与马斯京根汇流模型耦合，输入节点为当前时刻预报流量和实测值，网络采用双隐层模式，隐含层节点为4和10，修正预报前1个时刻主河道的7个区间入流，设置单次修正幅度最大不超过20%。

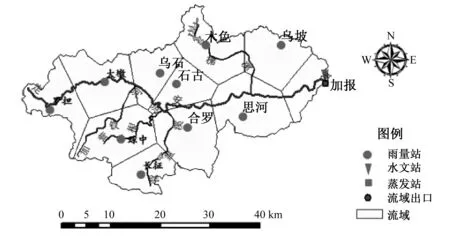
图1 定安河流域泰森多边形划分图Fig.1 Thiessen polygon partition of Dingan River watershed

2.3 模型率定

保留新安江模型和马斯京根汇流模型计算过程中的所有中间变量作为学习样本，选取10场次洪率定，10场次洪验证的交叉验证方式，设置初始学习效率系数0.1，动量系数0.15，采用均方根误差作为判断准则，目标精度0.01，最大循环次数10 000 次，经多次率定网络在1200次左右时即达到最优值，全局误差变化见图2。由图可知，率定数据和验证数据的误差均一致下降说明网络训练效果较好，且该算法收敛迅速，相较传统算法数万次的循环次数改进明显。

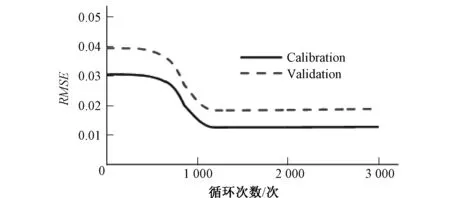
图2 神经网络交叉验证过程误差变化图Fig.2 Error variation of neural network cross validation process

2.4 单时段修正检验

单时段修正检验的目的在于验证模型的稳定性，上游各河段区间入流的修正结果将在多个时段后才会显现出来，如果模型输出的修正量存在较大误差，只看当前时刻的修正结果可能掩盖模型本身的缺陷。为达到这个目的，保留整场次洪的所有中间变量，每个时段进行一次修正后不再修正，同时记录下当前时刻，2 h之后、4 h之后的改善结果，记为BPCQ0、BPCQ2和BPCQ4。修正效果指标采用百分比偏差和纳什效率系数，验证期10场次洪的单时段修正效果见表1。

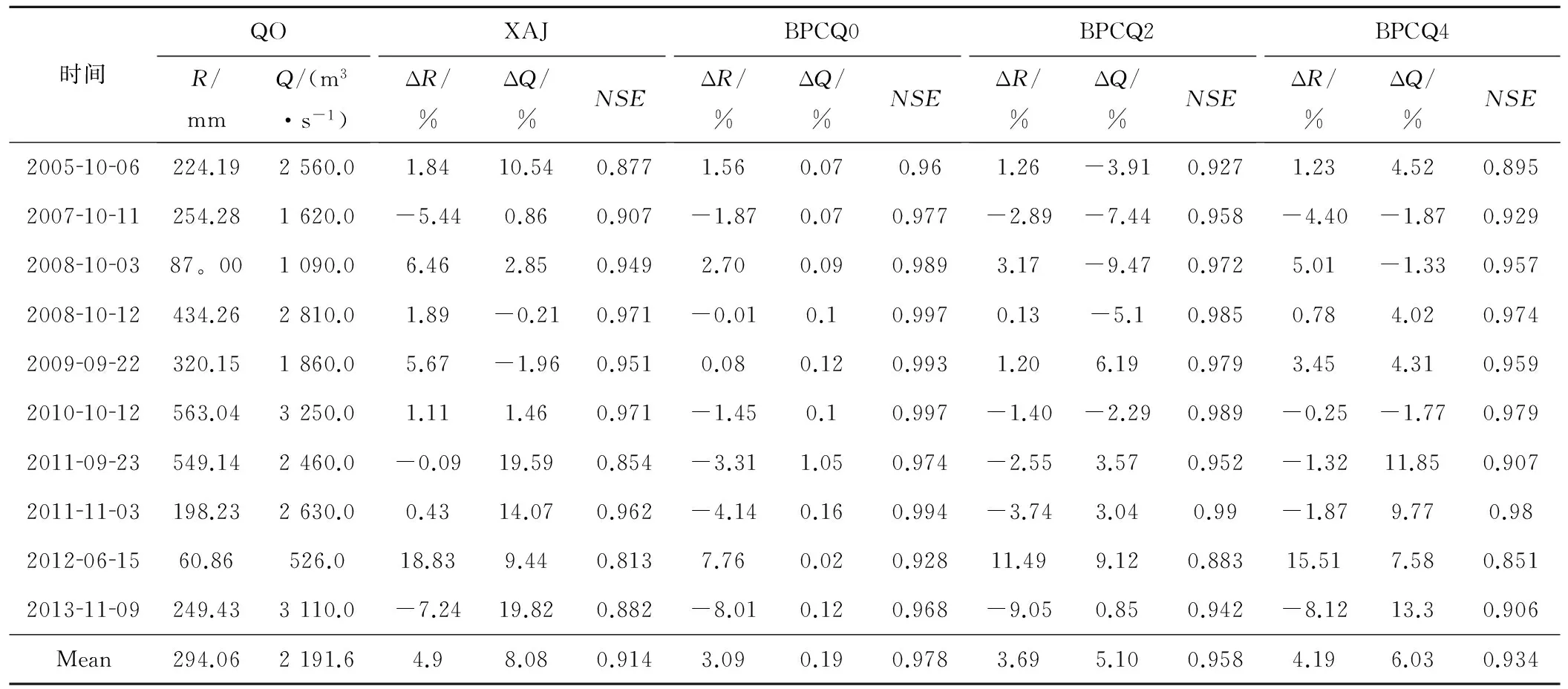
表1 验证期单时段耦合修正结果统计表Tab.1 Statistics for the accuracy of single period coupling correction during calibration period

注：“Mean”这一栏，ΔR和ΔQ的均值为绝对值的平均值，并非直接相加后求平均。

由表1可知：定安河流域经过多次人机交互率定后，XAJ模型直接计算后模拟结果的平均NSE达到0.914，模拟效果较好，但存在多场洪水洪峰偏离较大的情况。BP神经网络耦合修正后，ΔR的平均偏差BPQC0为3.09%，BPCQ2为3.69%，BPCQ4为4.19%相较修正前4.9%的偏差略有下降，且最大偏差由18.83%降低为BPCQ0的-8.01%，BPCQ2的11.49%和BPCQ4的15.51%。在洪峰方面，BPCQ0的ΔQ均值较修正前的8.08%降低到0.19%，BPQ2降低到5.1%，BPQ4的ΔQ也仅为6.03%，说明洪峰预报精度提升显著。BPCQ0的平均NSE达到了0.978，BPQ2为0.958，BPQ4为0.934均高于修正前的0.914，说明耦合修正模型的修正效果确实具有持续作用。

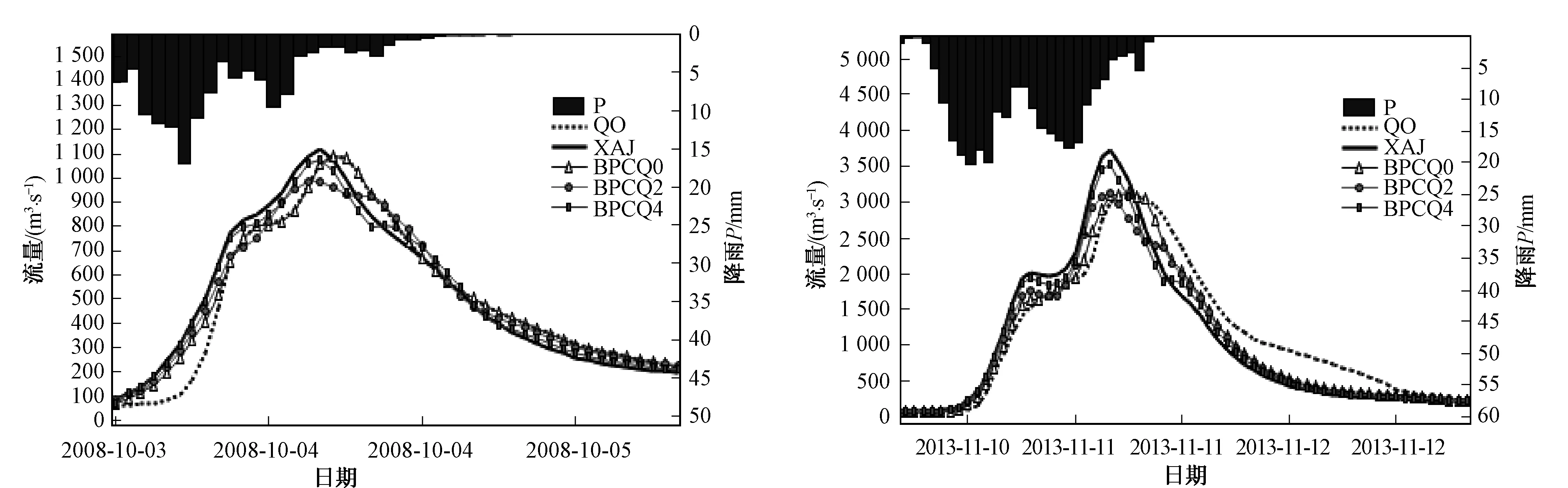
图3 次洪20081003和20131109单时段修正结果对比图Fig.3 single period coupling correction comparison of the flood 20081003 and 20131109

2.5 实时修正检验

实时修正检验的目的在于验证模型在实际应用中的可靠性，分别采用BP耦合修正和二阶AR模型对定安河流域的20场次洪进行实时修正。二阶AR模型选用最近5个时段的误差信息对预报结果进行动态修正，因为AR模型的修正效果随着预见期增加会明显下降，故选取修正后最近一个时段的预报结果进行对比分析，验证BP耦合修正算法的可靠性，实时修正检验结果见表2。由表2可知：修正后，径流深平均偏差由6.08%分别降为BPC的2.03%和AR(2)的2.91%；在洪峰方面，BPC由XAJ模型ΔQ均值的10.19%降低为2.65%，AR(2)则降低为4.94%。平均NSE的提升方面，BPC由修正前的0.894提高到0.985，AR(2)则为0.97。

综上可见，BP耦合修正算法在定安河流域的实时修正检验过程中，径流深、洪峰和NSE指标方面均较二阶AR模型更优，该算法的可靠性得到验证。

表2 定安河流域20场次洪实时修正结果对比Tab.2 Comparison of results of real-time updating for 20 floods of Dingan River watershed

注：“Mean”这一栏，ΔR和ΔQ的均值为绝对值的平均值，并非直接相加后求平均。

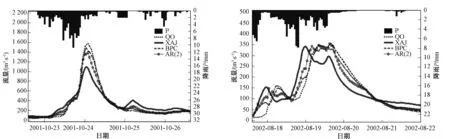
图4 次洪20011021和20020817实时修正结果对比图Fig.4 Real-time updating comparison of the flood 20011021 and 20020817

3 结 语

本文提出将BP神经网络与马斯京根汇流模型耦合修正的新方法，该算法收敛迅速且不损失预见期，拓展了BP神经网络算法在实时修正领域的应用。选取海南省定安河流域作为研究区，通过单时段修正检验构建三种对比方案，证明了该算法的修正效果具有稳定性，实时修正检验的结果表明该算法在径流深、洪峰和纳什效率系数方面的精度均有一定提升，在修正效果方面整体优于二阶AR模型，是一种可靠的修正算法，具有进一步研究的价值。

□

[1] 包为民.水文预报[M].北京：中国水利水电出版社,2006.

[2] 卢韦伟,周建中,陈 璐,等.考虑预报因子选择的神经网络降雨径流模型[J].水电能源科学,2013,31(6):21-25.

[3] 王 炎,王船海,王 妮,等.BP神经网络在感潮河段水动力洪水预报中的应用[J].水力发电,2016,42(2):21-25.

[4] 郑春成.汤河水库实时洪水预报技术研究[J].水利信息化,2012,(3):37-39.

[5] 韩 通,李致家,刘开磊,等.山区小流域洪水预报实时校正研究[J].河海大学学报(自然科学版), 2015,43(3):208-214.

[6] Si W, Bao W, Gupta H V.Updating real-time flood forecasts via the dynamic system response curve method[J]. Water Resources Research, 2015,51(7):5 128-5 144.

[7] 陈 攀,姜志群.AR模型在宝珠寺水库实时洪水预报校正中的应用[J].水利信息化,2014(3):41-44.

[8] 韩力群.人工神经网络教程[M].北京：北京邮电大学出版社, 2006.