传送带单线成型机的张力控制系统

王雅琳，陈冬冬，邓元，谢永芳



传送带单线成型机的张力控制系统

王雅琳，陈冬冬，邓元，谢永芳

(中南大学信息科学与工程学院，湖南长沙，410083)

针对传送带单线成型机放卷过程线绳张力不稳定、排线不均匀等问题，设计传送带单线成型机的放卷张力控制系统，建立该放卷张力控制系统的数学模型，并根据自抗扰控制技术对张力控制器进行设计，最终提出基于差分进化算法的自抗扰控制器参数优化方法。研究结果表明：所设计的放卷张力自抗扰控制器比传统的PID控制器具有更好的鲁棒性和抗干扰性，更能适应传送带单线成型机的张力控制。

传送带单线成型机；张力控制系统；自抗扰控制；差分进化算法

在传送带生产过程中，采用定张力成型设备是保证线绳张力稳定和排线均匀的重要手段。若线绳张力不稳定、排线不均匀，则不能共同承担外力，传送带强度低，抗撕裂性能差[1]。目前，国内传送带生产行业主要采用的控制方式为：收卷处的电动机带动收卷滚筒牵引钢丝线绳进行放卷和收卷缠绕；放卷处利用磁粉制动器产生放卷滚筒阻力矩，使得线绳产生一定张力，同时在收卷滚筒上设置排线槽实现线绳均匀排线。这种方式未考虑阻力矩在一定情况下放卷线圈半径变化导致线绳张力也随之变化的情况。另外，排线过程中线绳进入角度不断改变使得受到的挤压、摩擦力等不均匀，也会导致线绳张力不稳定[2]。为了解决上述张力控制存在的问题，近年来，一些特殊控制方法在张力控制中得到了广泛应用。胡亚伟[3]设计了基于神经网络的张力控制器，张永胜等[4]将模糊控制应用到纤维缠绕张力控制中，史廷永[5]应用鲁棒控制实现了凹印机速度与张力的解耦。但是，这些控制方法都需要人为地选定权函数或者必须具备较完善的控制规则才能得到较好的控制效果。此外，传送带单线成型机放卷张力控制系统是一个动态过程复杂、时变、非线性的系统，而且干扰因素多，控制难度大。因此，如何设计一个具有较好内部鲁棒性和抗干扰性的控制器也是传送带成型机张力控制需解决的问题。自抗扰控制技术是韩京清[6−7]针对PID控制器的不足而提出的一种估计补偿不确定因素的控制技术。自抗扰控制器具有较强的适应性和鲁棒性，尤其针对存在大干扰、强耦合以及不确定性的系统，优势更突出。韩京淸[8]将自抗扰控制技术用于钢球磨制粉控制系统，纪恩庆等[9−10]利用自抗扰控制器用于粗纱机和双机架铝带冷连轧张力控制。这些仿真结果表明自抗扰控制器的鲁棒性和抗干扰能力较强。因此，研究基于自抗扰控制技术的张力控制器设计具有很重要的实际意义。本文研究的传送带成型机目前采用的生产方式是通过收卷处的电动机带动收卷滚筒牵引钢丝线绳进行放卷和收卷缠绕；在放卷处利用磁粉制动器产生放卷滚筒阻力矩，使得线绳产生一定的张力；同时，为了保证线绳的排列均匀，在收卷滚筒上设置排线槽实现线绳均匀排线。经测试发现，这种生产方式生产出来的传送带存在外型形变较大、拉伸强度和使用寿命较低等问题，产品质量较差，合格率低。为此，本文作者设计传送带单线成型机的放卷张力控制系统，并利用自抗扰控制技术对张力控制器进行设计，同时针对自抗扰控制器参数难整定的问题，采用基于差分进化算法的自抗扰控制器参数优化方法。通过仿真实验验证自抗扰控制器在传送带张力控制中的性能。

1 传送带放卷张力控制系统的设计及建模

针对上述传统传送带成型机张力控制系统的不足，设计以磁粉制动器为执行机构、张力传感器为检测机构、滚珠丝杠排线器为排线机构的传送带单线成型机放卷过程张力控制系统，并建立该张力控制系统的数学模型。

1.1 放卷张力控制系统的设计

本文设计的传送带单线成型机放卷过程张力控制系统硬件结构如图1所示。

由图1可知一个完整的传送带张力控制系统由线绳放卷滚筒、收卷滚筒、张力传感器、张力控制器、磁粉制动器、滚珠丝杠排线机构和辅助装置组成。线绳放卷滚筒和收卷滚筒是张力控制系统的主要机构。张力传感器作为检测机构实时检测张力信号，并予以反馈，形成张力的闭环控制，以满足高精度控制要求。张力控制器是张力控制系统的核心，根据控制要求对检测到的张力信号进行处理，并输出合适的控制信号。磁粉制动器是系统的执行机构，根据张力控制器的输出信号，增大或者减小输出力矩，完成系统的控制。滚珠丝杠是系统的排线装置，采用步进电机带动丝杠牵引排线器移动，保证线绳等间距、平整的排列以及线绳的直线度，从而保证传送带成品的外观和质 量[11]。辅助装置包括驱动电机、牵引滚筒、支撑滚筒等，可用于提高控制系统的控制精度和稳定性。

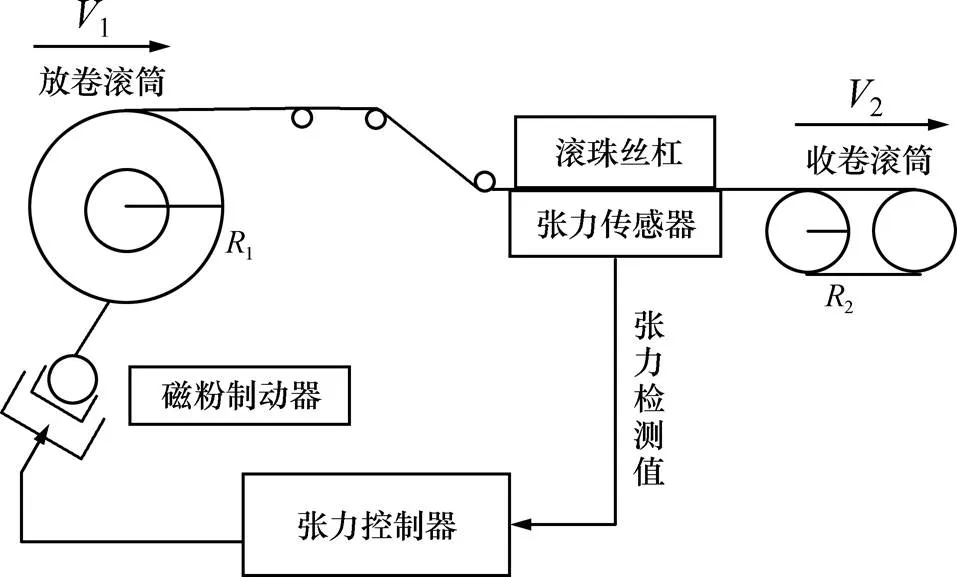
图1 传送带单线成型机放卷张力控制系统硬件结构

1.2 放卷张力控制系统的建模

传统的张力控制系统数学建模均是利用动态转矩平衡方程对系统运行过程中滚筒的运行动态进行分析得到。这种建模方式只单纯考虑了外力对线绳等物料的影响，而忽略了对线绳本身的分析。本文采用较全面的建模方式。首先根据胡克定律和质量守恒定律，通过分析系统运行过程中线绳的变化情况，建立线绳张力数学模型；再结合传统张力控制系统建模方式，利用动态转矩平衡方程，建立滚筒的动力学数学模型，最终得到所需的传送带成型机放卷张力控制系统的数学模型[12−14]。

1.2.1 线绳张力数学模型

基于胡克定律得到线绳的张力表达式：

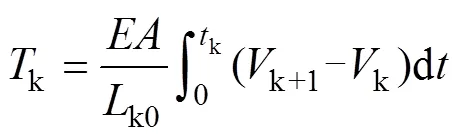
式中：为线绳弹性模量；为线绳横截面积；V+1和V分别为第+1个滚筒和第个滚筒的线速度；T为第+1个滚筒和第个滚筒间线绳产生的张力；L0为第+1个滚筒和第个滚筒间线绳未拉伸的原始长度；t为线绳经过相邻第个滚筒和第+1个滚筒所用的时间。

仅根据胡克定律建立的线绳张力数学模型较简单，且物理意义易理解。为了获得更准确的张力数学模型，本文利用胡克定律作为建模的理论依据，以前后相邻两滚筒间的线绳为研究对象，利用质量守恒定律可得到下列线绳张力数学模型：

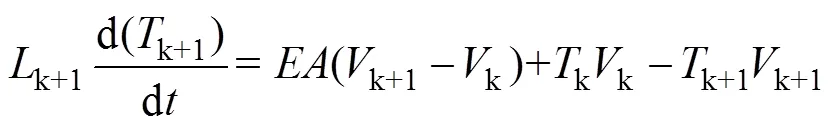
式中：L+1为个滚筒和第+1个滚筒之间线绳的长度。与单纯运用胡克定律相比，基于质量守恒定律得到的张力模型更加准确，更能真实地反映线绳速度与张力之间的关系。

1.2.2 放卷过程动力学数学模型1

放卷过程物理模型如图2所示。其中，1为放卷半径；2为线绳张力；1为线绳初始张力；R为磁粉制动器输出制动力矩；1为放卷滚筒的摩擦因素；F为摩擦力矩；1为放卷角速度；1为放卷滚筒放卷线速度；2为收卷端从动电机速度(恒值)即收卷滚筒线速度；0为放卷滚筒半径。

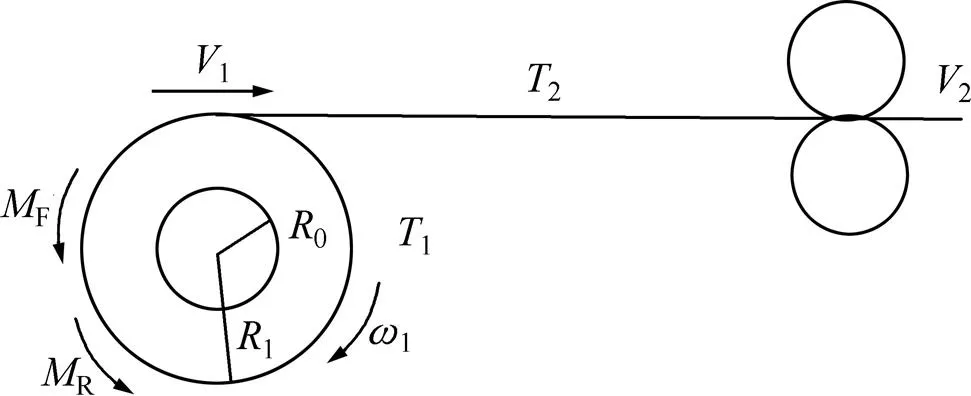
图2 放卷过程物理模型

由转矩平衡原理可得如下放卷滚筒动力学模型：

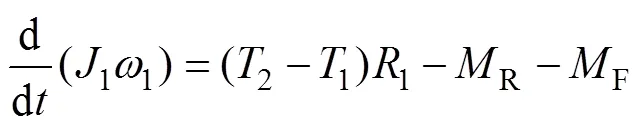
式中：1为放卷滚筒转动惯量；

1.2.3 传送带放卷过程数学模型

传送带单线成型机放卷过程张力系统示意图如图3所示。

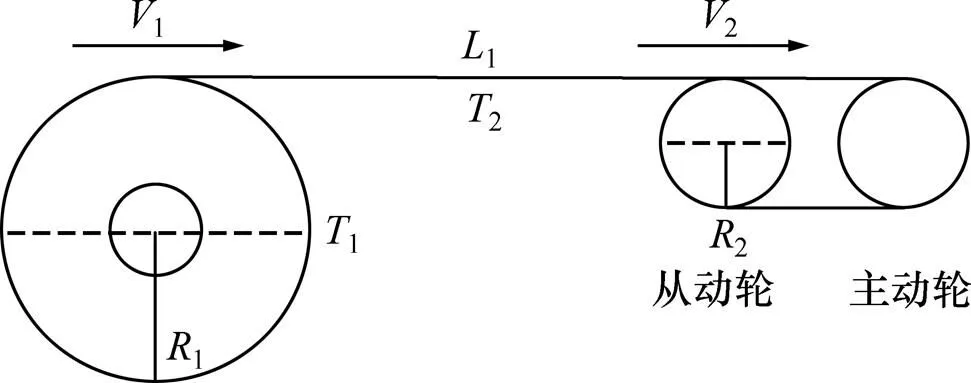
图3 传送带单线成型机放卷过程张力系统示意图

综合建立的张力模型和放卷过程动力学数学模型，得到放卷过程动力学数学模型如下：

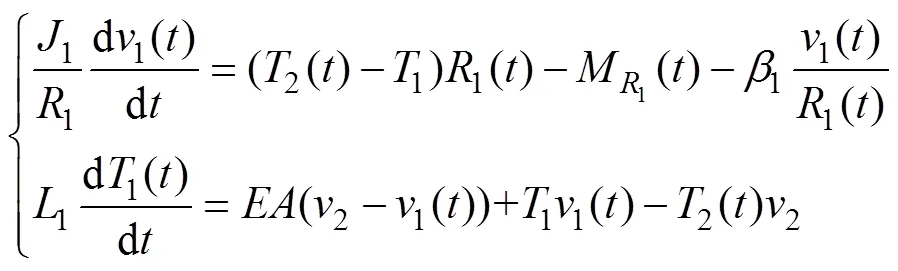
2 自抗扰控制技术研究及参数优化

2.1 自抗扰控制技术原理

自抗扰控制器的结构分为跟踪微分器(TD)、非线性状态误差反馈(NLSEF)和扩张状态观测器(ESO)等 3部分，分别发挥不同作用。组合能自动估计并补偿系统扰动的自抗扰控制器[15−17]。自抗扰控制器的结构如图4所示。

针对下列常见二阶系统进行研究：

典型二阶自抗扰控制器的完整离散算法如下。

1) 跟踪微分器TD安排系统设定值0()的过渡过程，建立离散化的离散跟踪器模型，如式（6）所示，并称其为最速离散跟踪微分器。

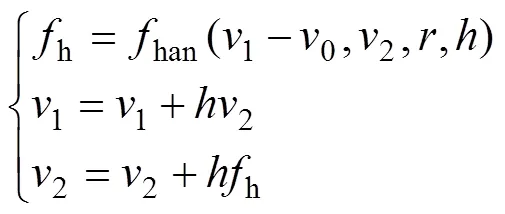
其中：为采样步长；为根据系统承受能力所选择的决定跟踪速度的参数，称为快速因子；为最速控制综合函数，

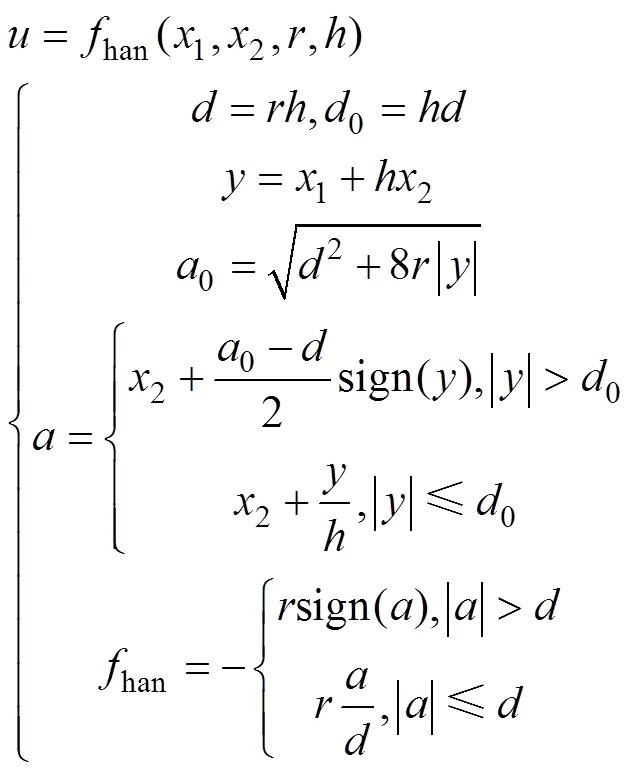
2) 扩张状态观测器ESO利用系统的输入和输出来跟踪、估计系统的状态和扰动，建立的扩张观测器如下：

(8)

其中：

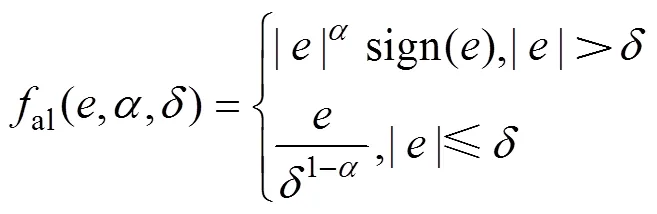
3) 非线性状态误差反馈为

(10)

4) 扰动补偿控制量为

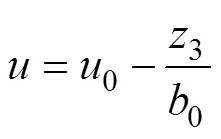
从自抗扰控制器的离散算法中可以看出自抗扰控制器3个组成部分的参数都较多。为了更好地应用自抗扰控制器，很有必要了解各参数对控制性能的影响，并确定其中关键性参数。

2.2 基于差分进化的自抗扰控制器参数优化

自抗扰控制器虽然参数较多，但对控制性能起关键作用的主要是跟踪微分器的参数和1，扩张状态观测器的参数1，2和3，非线性状态误差反馈的参数01和02，其他控制器参数可以根据调试经验或者被控对象的要求设置。目前针对自抗扰控制器参数的优化的研究虽然取得了一定进展，但还没有形成比较系统的方法，在大多数情况下还是依赖人工经验进行调整，调整过程既繁琐又难以保证可靠性，因此，可通过智能优化算法对这些关键性参数进行优化。由于差分进化算法具有较强的鲁棒性和全局搜索能力，本文采用差分进化算法优化自抗扰控制器参数。

差分算法的基本原理是通过对当前种群个体进行突变、交叉，生成试验个体向量(后代)，通过选择决定试验个体向量是否成为下一代种群的个体[18−21]。

2.2.1 种群初始化

在差分进化算法中，种群初始化的目的是建立全局优化搜索的初始点。种群个体特征属性一般用P个维的实数值向量来描述，第代种群个体。其中：=1，2，…，P；为代种群个体的第个属性。

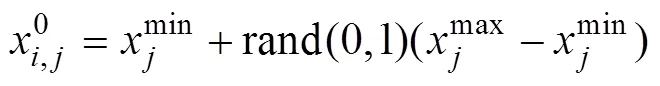
2.2.2 变异

变异操作实际上是第代种群中每个目标向量,G相互间的竞争、干扰，生成下代种群的个体目标向量。研究者在研究差分策略时提出多种变异操作，其中DE/rand/1/bin差分策略因其具有较快的收敛速度和较强的鲁棒性，能有效地保持种群的多样性，被众多的学者采用(其中，DE为差分进化算法的简称，rand表示当前被选定的变异向量为随机生成，表示差分策略差分向量个数，bin表示交叉模式)。

差分进化算法中个体的进化方向是不确定的，当种群个体在有边界条件约束情况下，突变的下一代种群可能会出现不符合边界条件约束的新个体，因此，在研究种群个体突变时，有必要考虑新个体边界条件溢出的情况。其中，最简单的办法就是用随机产生的个体目标向量代替不符合条件的突变个体目标向量，即或，当时，有

2.2.3 交叉

差分进化算法中的交叉操作主要是为了增加种群个体目标向量的多样性，对第代种群个体的目标向量,G及其变异生成的新种群个体的目标向量,G+1进行个体间的相互交叉操作，得出新的试验目标向量，

2.2.4 选择

差分进化算法选择策略的核心是当前种群个体,G与试验个体,G+1进行适应度竞争，选出下代种群个体目标向量,G+1：

式(14)为基于最小值问题提出的选择策略，其中(∙)为适应度函数。当时，测试个体适应能力优于当前种群个体，并取代当前种群个体进入下代种群；否则，测试个体被淘汰，当前种群个体进入下代种群。

基于差分进化算法的自抗扰控制器参数优化，目标函数选择为系统实际输出与期望输出的绝对误差对时间的积分：

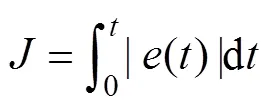
基本算法流程如下。

Step 1：相关参数的初始化。这些参数包括种群大小P、变异因子、交叉因子R、最大迭代次数m、所求问题的维数等。

Step 2：随机产生初始化种群。

Step 3：变异操作。每个个体进行变异操作，产生变异个体。

Step 4：交叉操作。对每个个体进行交叉操作，生成试验个体。

Step 5：选择操作。比较目标个体和试验个体的优劣，选择较优者作为下一代新的个体。

Step 6：完成1次迭代，判断迭代次数是否达到最大值，若未达到则返回Step 3，再次迭代优化；若达到最大迭代次数，则优化结束，输出最终最优个体，也就是优化后的自抗扰控制器的控制参数。

差分进化算法迭代曲线如图5所示。从图5可见：随着迭代次数增加，系统的跟踪误差不断减小，说明目标函数值不断收敛。

图6所示为优化参数后的自抗扰控制器对系统的阶跃响应曲线。由图6可知：采用差分进化算法优化参数的自抗扰控制器能快速响应，跟踪误差小，有很好的跟踪性能。

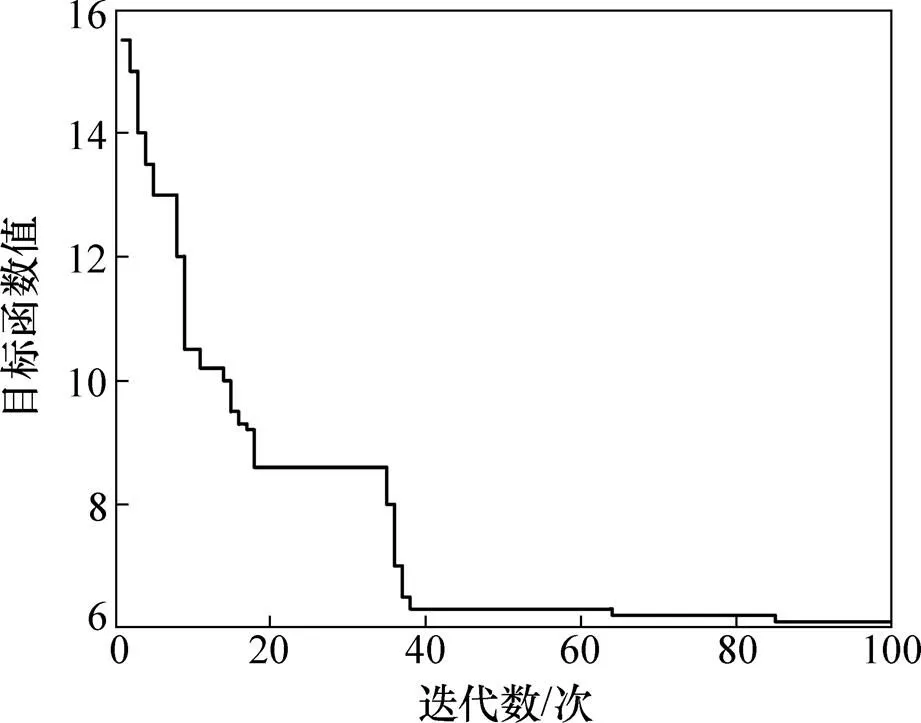
图5 基于差分进化算法的自抗扰控制器寻优过程示意图

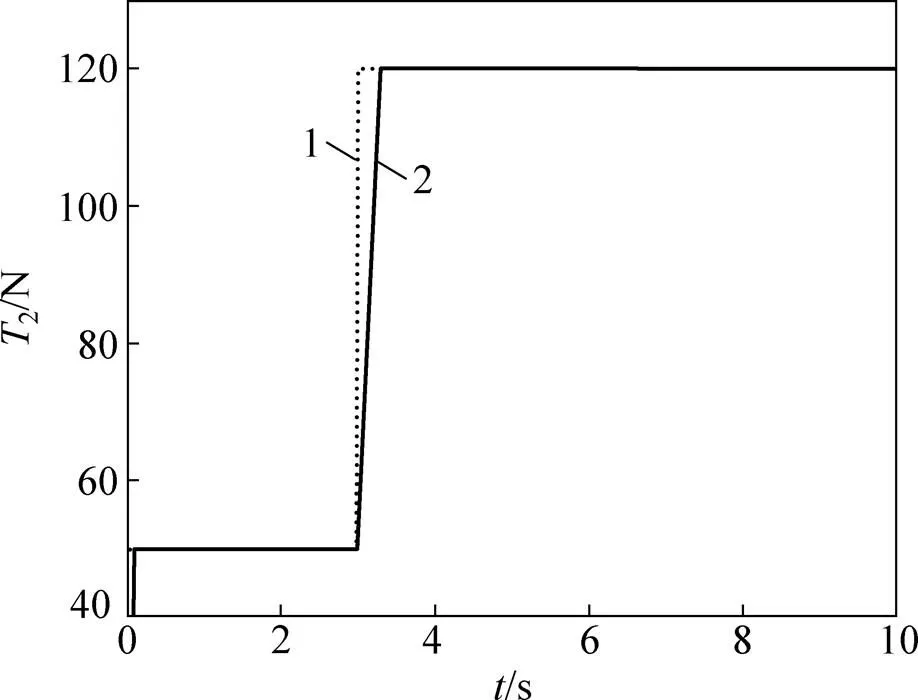
1—系统输入；2—系统响应。

3 仿真结果与分析

在Matlab/Simulink中建立传送带放卷过程自抗扰控制系统的仿真模型。传送带放卷自抗扰控制系统仿真模型如图7所示，其中，1和2模块分别表示跟踪微分器的参数和1；3和4模块分别表示非线性状态误差反馈的参数01和02；5，6和7分别表示扩张状态观测器的参数1，2和3；Subsystem1模块表示式(4)中的放卷过程模型。

3.1 鲁棒性仿真

鲁棒性仿真中首先设置参数1=0.3 m，2分别为0.1 m/s和0.2 m/s，比较自抗扰控制器和PID控制器对2阶跃输入的控制效果。仿真结果分别如图8(a)和图8(b)所示。

从图8(a)可见：在不同收卷速度和自抗扰控制下，放卷张力2都能很快地跟随系统输入。从图8(b)可见：在PID控制下，当收卷速度增大时，放卷张力2波动增大，且响应时间变长。

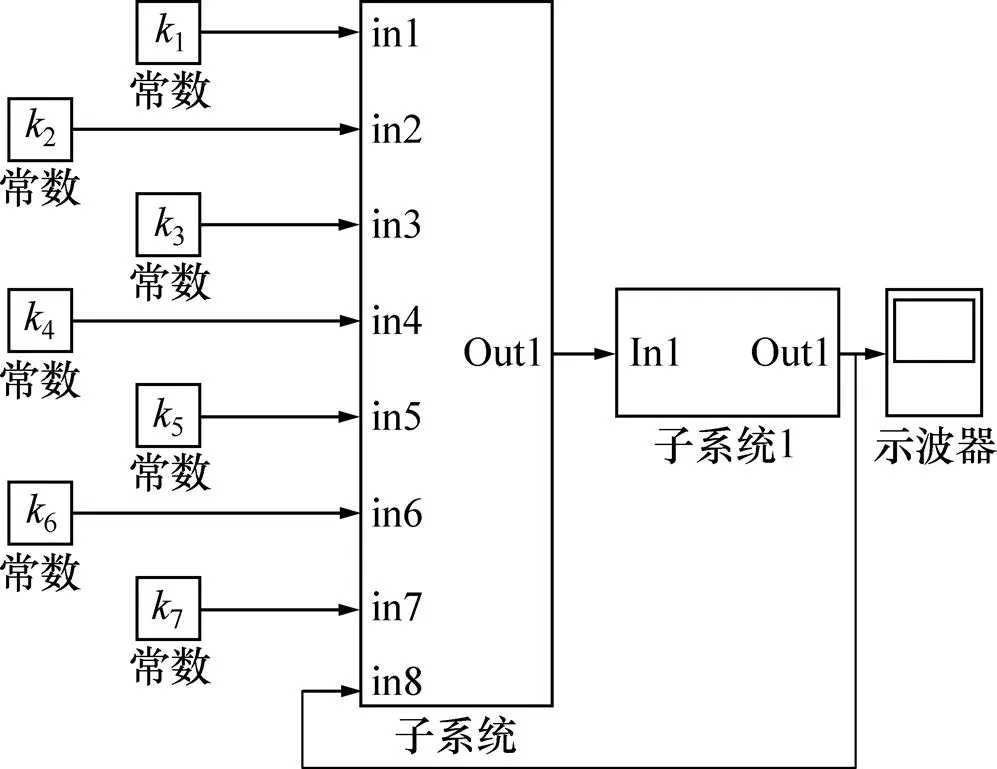
图7 传送带放卷自抗扰控制系统仿真模型

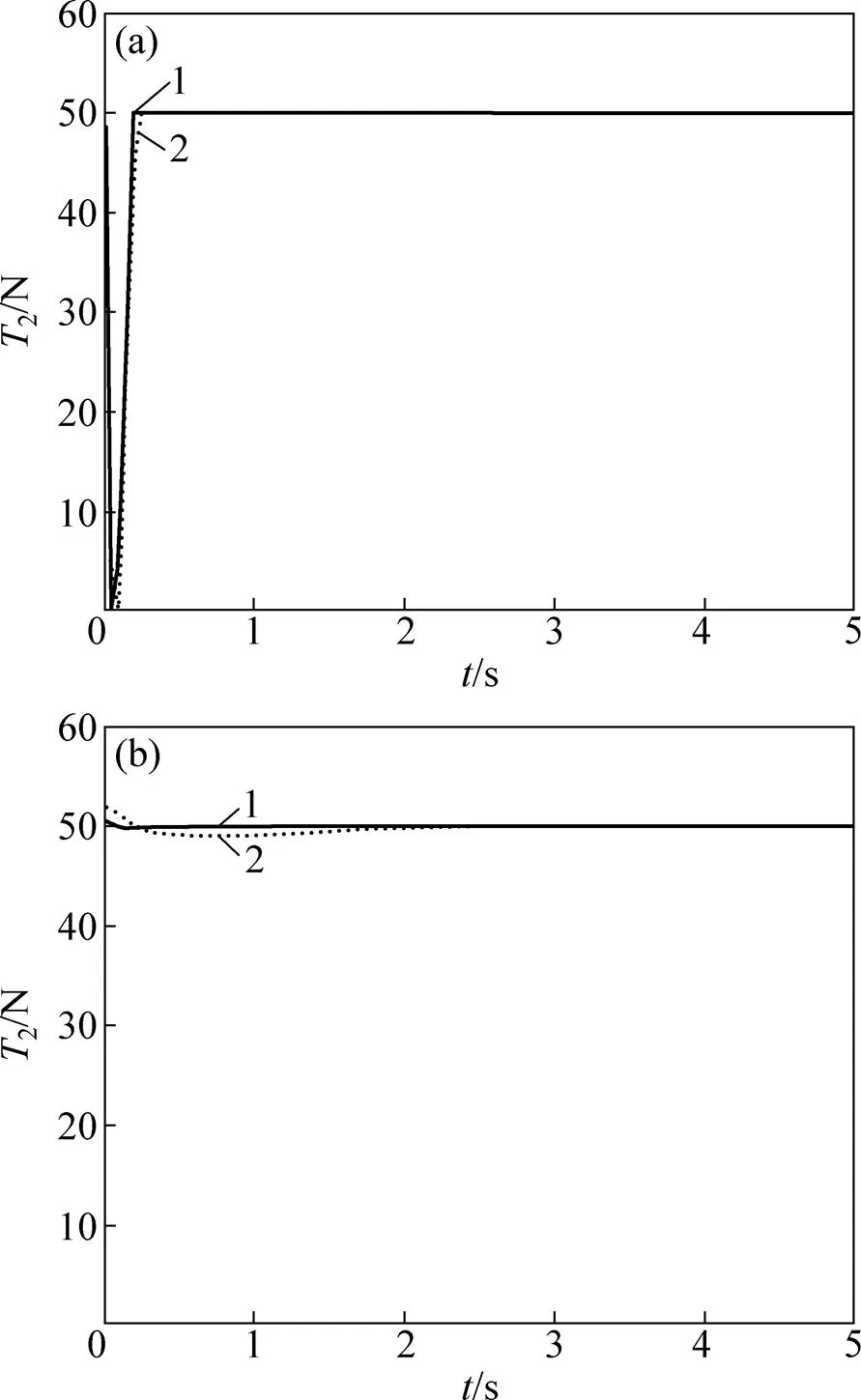
(a) 自抗扰控制器；(b) PID控制器

设置另一组参数：2=0.1m/s，1分别为0.2m和0.3 m。比较自抗扰控制器和PID控制器对2的阶跃输入的控制效果，仿真结果如图9所示。

从图9(a)可见：在不同放卷半径和自抗扰控制下，放卷张力2都能很快地跟随系统输入，并且波动变化不大，稳定性基本不受影响。从图9(b)可见：在PID控制下，当放卷半径增大时，系统超调变大，3s左右才能稳定在50 N，响应时间变长。这说明自抗扰控制器比PID控制器具有更好的鲁棒性，控制性能受系统参数变化的影响小，对参数的敏感性低。

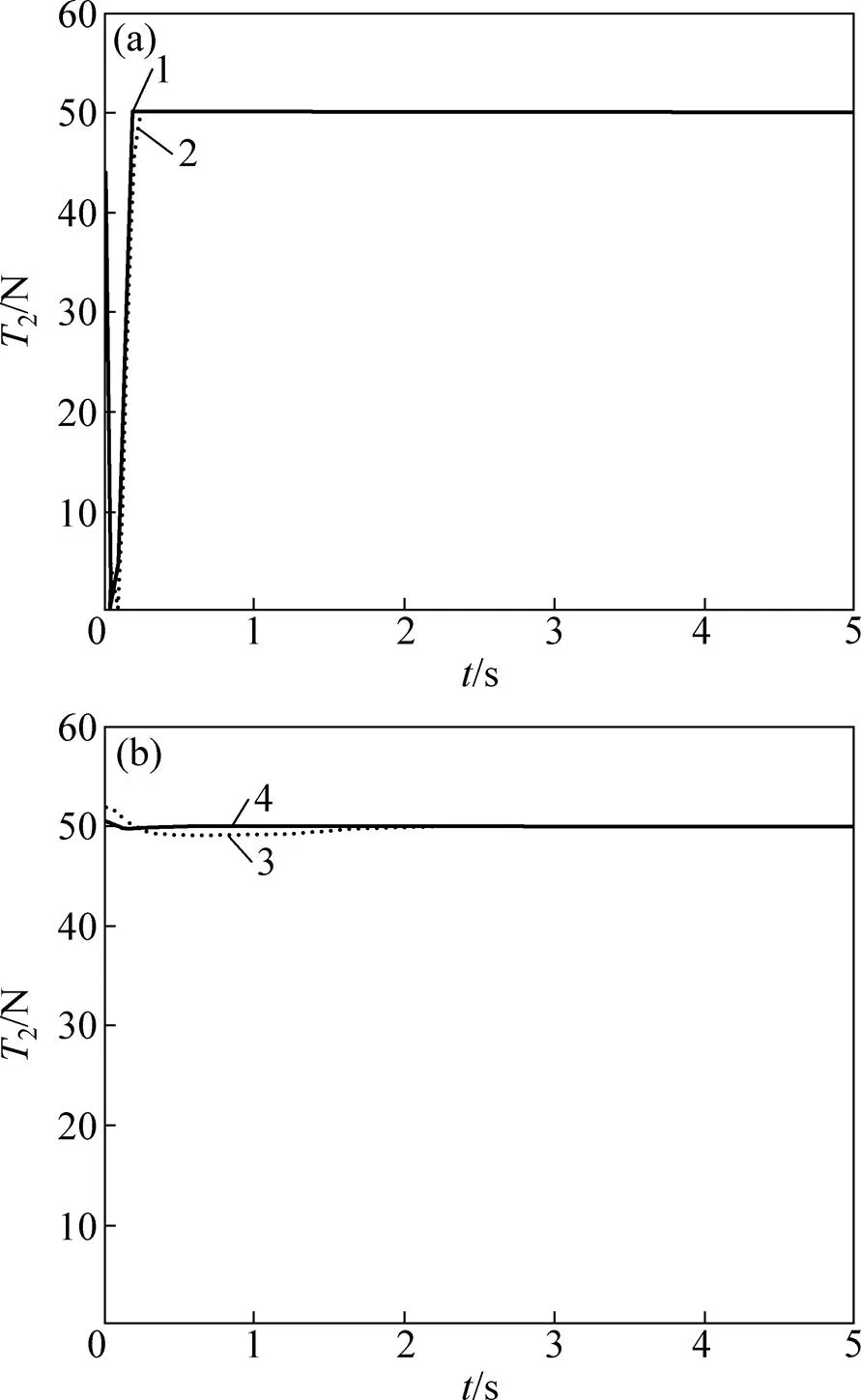
(a) 自抗扰控制器；(b) PID控制器

3.2 抗干扰性仿真

抗干扰性仿真中首先设置：1=0.3 m，2=0.1 m/s。在5 s时给传送带张力控制系统强度为5 N的阶跃干扰，比较自抗扰控制器和PID控制器的抗干扰性，仿真结果分别如图10和图11所示。

从图10可见：在PID控制下，阶跃干扰使得2产生了强度为1.5 N的波动，且波动时间持续了1 s。从图11可见：采用自抗扰控制时，阶跃干扰使得2产生了1个强度为1 N左右的瞬时波动，2迅速稳定到50 N。由此可见：相比于PID控制，自抗扰控制系统受干扰时产生的波动更小，系统响应更快，并且能迅速地回到稳定状态，说明自抗扰控制器比PID控制器具有更强的抗干扰性。

上述鲁棒性仿真与抗干扰性仿真实验结果说明自抗扰控制器自抗扰控制技术对系统内部参数的变化不敏感，鲁棒性较强，同时具有更强的抗干扰性。

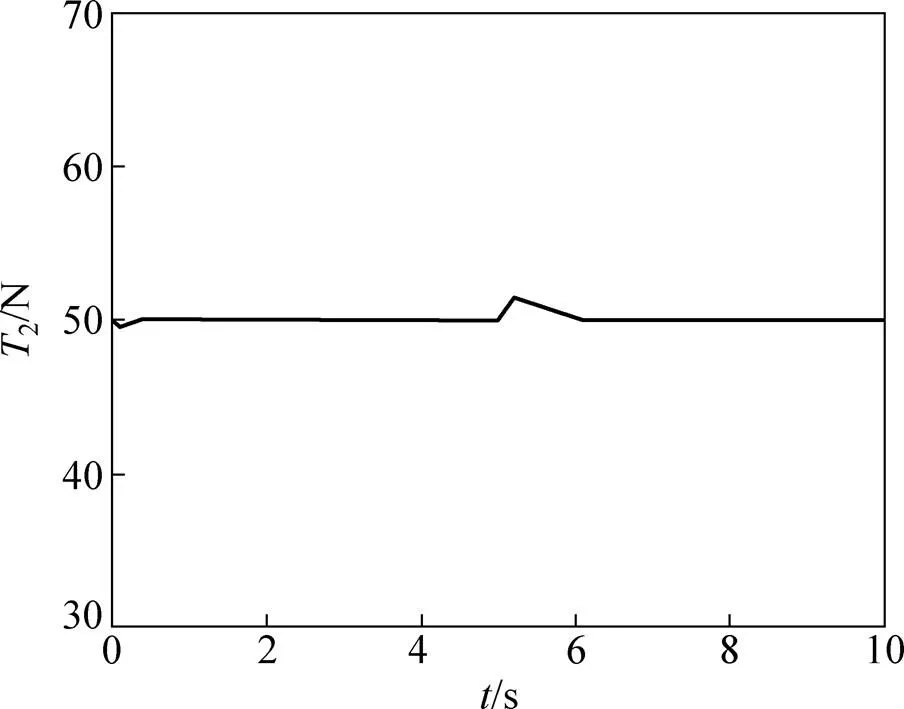
图10 PID控制的响应曲线

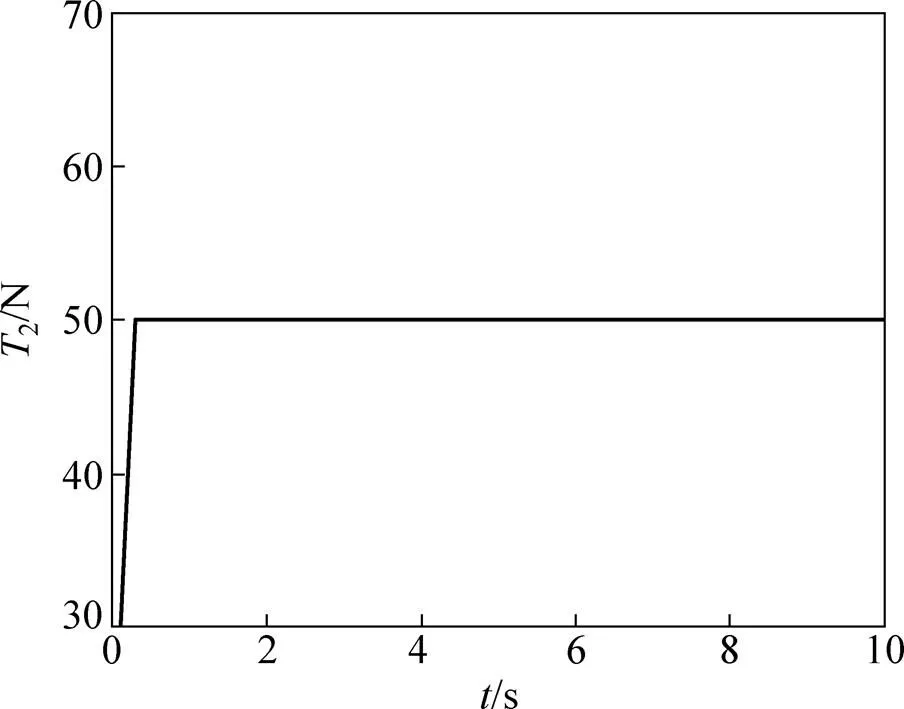
图11 自抗扰控制的响应曲线

4 结论

1) 针对传送带单线成型机生产现状以及对张力控制稳定性、排线均匀性的要求，研究了传送带单线成型机放卷过程的张力控制系统。设计并改善了放卷过程张力控制系统的硬件结构；根据胡克定律和质量守恒定律，建立了线绳张力数学模型；并利用动态转矩平衡方程，推导出滚筒的动力学数学模型，从而建立了传送带成型机放卷张力控制系统的数学模型，并设计了放卷张力自抗扰控制器。

2) 为提高控制性能，采用差分进化算法对自抗扰控制器关键参数进行优化。鲁棒性和抗干扰性仿真结果说明了自抗扰控制器相比于PID控制器在传送带单线成型机张力控制上更具有优越性。

[1] 吴桂卿, 唐跃. 线绳张力对传动带性能影响的研究[J]. 机械传动, 2012, 36(5): 18−21. WU Guiqin, TANG Yue. Research on the effect of cord tension on the V-belt performance[J]. Journal of Mechanical Transmission, 2012, 36(5): 18−21.

[2] 杨娅君, 周晓辉. 传动带成型机张力控制系统比较[J]. 橡胶工业, 2003, 50(10): 606−608. YANG Yajun, ZHOU Xiaohui. Comparison of tension control system of belt forming machine[J]. China Rubber Industry, 2003, 50(10): 606−608.

[3] 胡亚伟. 基于BP神经网络的张力控制系统[D]. 长沙: 中南大学信息科学与工程学院, 2008: 34−57. HU Yawei. Tension control system based on BP neural network[D]. Changsha: Central South University. College of Information Science and Engineering, 2008: 34−57.

[4] 张永胜, 高宏力, 刘庆杰. 基于模糊控制理论的同步带恒张力控制系统[J]. 机械设计与制造, 2012, 50(6): 15−17. ZHANG Yongsheng, GAO Hongli, LIU Qingjie. Constant tension control system based on fuzzy control theory[J]. Machinery Design & Manufacture, 2012, 50 (6): 15−17.

[5] 史廷永. 基于∞鲁棒控制的凹印机张力控制系统研究[D]. 长沙: 中南大学信息科学与工程学院, 2009: 38−53. SHI Tingyong. The study of gravure printing machine control system based on∞robust control[D]. Changsha: Central South University. College of Information Science and Engineering, 2009: 38−53.

[6] 韩京清. 自抗扰控制技术[J]. 前沿科学, 2007, 1(1): 24−31. HAN Jingqing. Auto disturbances rejection control technique[J]. Frontier Science, 2007, 1(1): 24−31.

[7] 韩京清. 从PID 技术到“自抗扰控制”技术[J]. 控制工程, 2002, 9(3): 13−18. HAN Jingqing. From PID technique to active disturbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13−18.

[8] 韩京淸. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 243−347. HAN Jingqing. Active disturbance rejection control technique:the technique estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 243−347.

[9] 纪恩庆. 基于自抗扰控制器的粗纱机张力控制系统研究与应用[D]. 济南: 山东大学信息科学与工程学院, 2007: 48−59. JI Enqing. Research and application of tension control system of roving machine based on ADRC[D]. Jinan: Shandong University. College of Information Science and Engineering, 2007: 48−59.

[10] 陈菡萏, 张飞, 王京. 基于 LADRC 的双机架铝带冷连轧机张力控制研究[J]. 冶金自动化, 2015, 39(3): 30−33, 38. CHEN Handan, ZHANG Fei, WANG Jing. Research of tension control system of aluminum cold twin-stand mill based on LADRC[J]. Metallurgical Industry Automation, 2015, 39(3): 30−33, 38.

[11] HUANG Yi, XUE Wenchao, GAO Zhiqiang, et al. Active disturbance rejection control: methodology, practice and analysis[C]//Control Conference (CCC), 2014. Nanjing: IEEE, 2014: 1−5.

[12] 刘善慧, 梅雪松, 杜喆, 等. 放卷张力系统解耦控制器的设计[J]. 西安交通大学学报, 2012, 46(9): 55−59. LIU Shanhui, MEI Xuesong, DU Zhe, et al. Decoupling controller design for unwinding tension system[J]. Journal of Xi’an Jiaotong University, 2012, 46(9): 55−59.

[13] LIU Shanhui, MEI Xuesong, KONG Fanfeng. Research on unwinding tension system control based on active disturbance rejection control[C]//2012 2nd International Conference on Materials, Mechatronics and Automation (ICMMA 2012), Nanchang, 2012: 252−257.

[14] 王世琛, 郑恩让. 合股机放卷张力系统自抗扰控制器设计[J]. 电子器件, 2014, 37(3): 535−538. WANG Shichen, ZHENG Enrang. Design of active disturbance rejection controller for the rewinding tension system on plying machine[J]. Chinese Journal of Electron Devices, 2014, 37(3): 535−538.

[15] HAN Jinqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900−906.

[16] 黄一, 薛文超. 自抗扰控制: 思想, 应用及理论分析[J]. 系统科学与数学, 2012, 32(10): 1287−1307. HUANG Yi, XUE Wenchao. Active disturbance rejection control: methodology, applications and theoretical analysis[J]. Journal of System Science and Math Science, 2012, 32(10): 1287−1307.

[17] 高志强. 自抗扰控制思想探究[J]. 控制理论与应用, 2013, 30(12): 1498−1510. GAO Zhiqiang. On the foundation of active disturbance rejection control[J]. Control Theory & Applications, 2013, 30(12): 1498−1510.

[18] 武雷, 保宏, 杜敬利, 等. 一种自抗扰控制器参数的学习算法[J]. 自动化学报, 2014, 40(3): 556−560. WU Lei, BAO Hong, DU Jingli, et al. A learning algorithm for parameters of automatic disturbances rejection controller[J]. Acta Automatica Sinica, 2014, 40(3): 556−560.

[19] 杨启文, 蔡亮, 薛云灿. 差分进化算法综述[J]. 模式识别与人工智能, 2008, 21(4): 506−513. YANG Qiwen, CAI Liang, XUE Yuncan. A survey of differential evolution algorithms[J]. Pattern Recognition and Artificial Intelligence, 2008, 21(4): 506−513.

[20] 刘波, 王凌, 金以慧. 差分进化算法研究进展[J]. 控制与决策, 2007, 22(7): 721−729. LIU Bo, WANG Ling, JIN Yihui. Advances in differential evolution[J]. Control and Decision, 2007, 22(7): 721−729.

[21] 万东. 差分进化算法研究及其应用[J]. 科学技术与工程, 2009, 9(22): 6673−6676. WAN Dong. Research and application based on differential evolution algorithm[J]. Science Technology and Engineering, 2009, 9(22): 6673−6676.

(编辑 陈灿华)

Unwinding tension control system of conveyor belt former

WANG Yalin, CHEN Dongdong, DENG Yuan, XIE Yongfang

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

A structure and control strategy in the unwinding tension control system of conveyor belt former was studied to enhance the tension stability and the uniformity of cords. A model of unwinding system was established according to the designed structure. And according to the model, the active disturbance rejection controll techique was used to design the tension controller, and then differential evolution algorithm was presented for tuning the parameters of the controller automatically. The results show that the proposed active disturbance rejection controller has better internal robustness and interference immunity than traditional PID controller in tension controll.

conveyor belt former; tension control system; active disturbance rejection control; differential evolutionalgorithm

10.11817/j.issn.1672−7207.2017.02.016

TP273

A

1672−7207(2017)02−0381−08

2016−02−15；

2016−04−22

国家自然科学基金资助项目(61273187)；国家自然科学基金创新研究群体科学基金资助项目(61321003)(Project(61273187) supported by the National Natural Science Foundation of China; Project(61321003) supported by the National Science Fund for Creative Research Groups)

王雅琳，博士，教授，从事复杂过程建模、优化与控制的研究；E-mail：ylwang@csu.edu.cn