利用沪深300股指期货对冲系统性风险的研究

李明书+张磊

【摘要】本文研究如何利用沪深300股指期货来对冲沪深300股票指数的风险，为跟踪沪深300指数的指数型基金提供一个对冲系统性风险的策略选择。首先，文章选用了BVAR、ECM、GARCH模型来选定套期保值比率，利用此比率可以建立由沪深300成分股多头和沪深300股指期货空头组合而成的资产组合。其次，文章考察了3种模型对应的资产组合的套期保值效率、和收益率波动性，发现除股灾期间外，对冲的效果较为理想。

【关键词】股指期货；套期保值；系统性风险

一、数据

本文选取了2015年1月5日到2015年12月31日的沪深300指数（St）和当月交割的沪深300股指期货（Ft）的日收盘价作为原始数据，然后对原始数据取对数收益率得到两组时间序列rSt和rFt，最终我们对这两组时间序列进行各种计量检验，以选择最好的对冲模型。

本文假设指数型基金管理者在投资沪深300成分股时，完全按照个股在沪深300指数中的权重来配置股票，并且在整个数据期间都使用同一种套期保值比率。

二、对冲模型的选取

本文所选用的对冲策略是“卖出套期保值”策略，投资者为防止股票价格下跌，在期货市场上卖出股指期货，用期货的盈亏来抵消股票现货的亏盈，从而达到保值目的。

计算套期保值比率的一種典型模式是双变量向量自回归（B-AR）模型，模型具体形式如下。

rSt=α+βrFt+ni=1rirS，t-1+ni=1θjrF，t-j+εt

其中β为最优套期保值比率。

但现货与期货之间的协整关系也会对套期保值比率的估计造成影响，而ECM模型对此效应有一定的改善，其具体模型为：

rSt=α+βrFt+ni=1rirS，t-1+ni=1θjrF，t-j+ωZt-1+εt

其中β为最优套期保值比率。

这两个模型都假设不存在异方差，不一定符合实际情况，因而我们对数据进行ARCH效应检验，如果存在ARCH效应，那么我们选用GARCH模型来计算套期保值比率，具体模型如下：

rSt=α+βrFt+εt?εt|Ωt-1~N（0，ht）

ht=α+qi=1riε2t-1+pi=1θjht-1

其中β为最优套期保值比率。

三、实证分析

（一）模型选取

（1）平稳性检验与B-VAR模型

①rSt与rFt的ADF检验：结果发现rSt与rFt不存在单位根，意味着它们是平稳序列。

②B-VAR模型实证检验

这里本文使用2阶双变量自回归模型，具体模型如下：

rSt=α+βrFt+ni=1rirS，t-i+ni=1θjrF，t-j+ωZt-1+εt

检验结果如下： 其中拟合优度为R2=0.78，从上面的结果可以看出rFt的系数为1.121413，t统计量和P值显示该系数显著不等于零，B-VAR模型的最优套期保值比率约为1.121413。

（二）协整检验与ECM模型

（1）rSt和rFt之间的协整性检验

我们首先对lnSt和lnFt进行平稳性检验，结果显示沪深300指数和沪深300股指期货指数的时间序列都是非平稳序列，而在前面我们分别对它们的日对数收益率序列进行了ADF检验，检验结果为平稳。这意味着他们的一阶差分序列均为时间平稳序列，于是我们可以对其进行EG协整性检验。

我们首先做以下回归：

lnSt=β0+β1lnFt+εt

然后对残差项进行ADF检验，结果显示残差项为平稳数列，这意味着lnSt和lnFt存在一阶协整关系。

（2）ECM模型

之间我们已经得到了如下回归：lnSt=β0+β1lnFt+εt，我们利用此回归的残差项作为ECM模型中的误差修正项，它反映了期货和现货之间的协整关系，该模型可以用以下回归来估计。

rSt=α+βrFt+ni=1rirS，t-i+ni=1θjrF，t-j+ωZt-1+εt

在此，我们使用的滞后阶数位2，由于截距项不显著，故删去截距项结果如下：

其中的拟合优度为R2=0.831860，从上表中我们可以看到rF的系数为1.082363，即最优套期保值率为1.082363。

（三）ARCH检验与GARCH模型

（1）沪深300指数的ARCH检验

首先观察沪深300指数日收益率的自相关和偏自相关图。

我们可以用如下方程来拟合。

rs，t=μ+10i=2rs，t-i+εt

回归后结果不显著，故将滞后项修改为4，方程即为

rs，t=μ+4i=2rs，t-i+εt

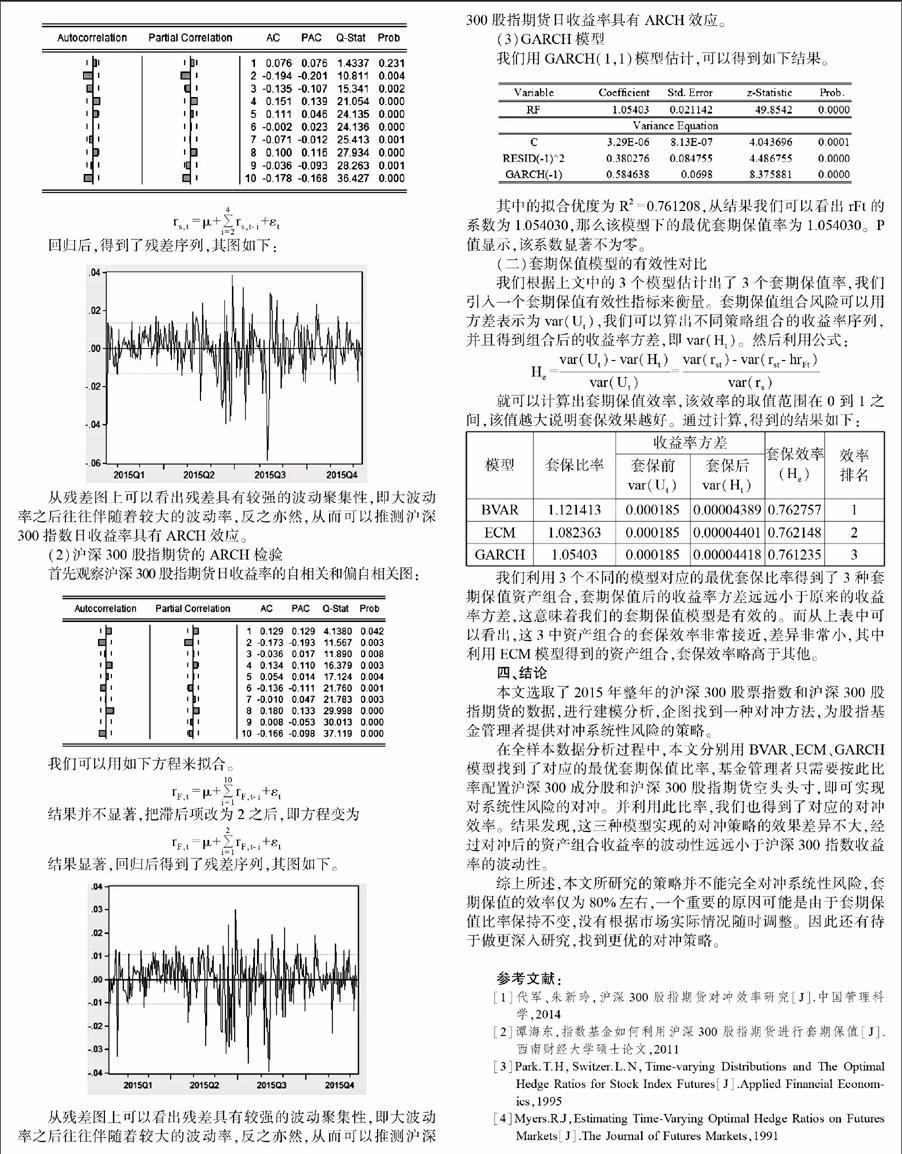
回归后，得到了残差序列，其图如下：

从残差图上可以看出残差具有较强的波动聚集性，即大波动率之后往往伴随着较大的波动率，反之亦然，从而可以推测沪深300指数日收益率具有ARCH效应。

（2）沪深300股指期货的ARCH检验

首先观察沪深300股指期货日收益率的自相关和偏自相关图：

我们可以用如下方程来拟合。

rF，t=μ+10i=1rF，t-i+εt

结果并不显著，把滞后项改为2之后，即方程变为

rF，t=μ+2i=1rF，t-i+εt

结果显著，回归后得到了残差序列，其图如下。

从残差图上可以看出残差具有较强的波动聚集性，即大波动率之后往往伴随着较大的波动率，反之亦然，从而可以推测沪深300股指期货日收益率具有ARCH效应。

（3）GARCH模型

我们用GARCH（1，1）模型估计，可以得到如下结果。

其中的拟合优度为R2=0.761208，从结果我们可以看出rFt的系数为1.054030，那么该模型下的最优套期保值率为1.054030。P值显示，该系数显著不为零。

（二）套期保值模型的有效性对比

我们根据上文中的3个模型估计出了3个套期保值率，我们引入一个套期保值有效性指标来衡量。套期保值组合风险可以用方差表示为var（Ut），我们可以算出不同策略组合的收益率序列，并且得到组合后的收益率方差，即var（Ht）。然后利用公式：

He=var（Ut）-var（Ht）var（Ut）=var（rst）-var（rst-hrFt）var（rs）

就可以計算出套期保值效率，该效率的取值范围在0到1之间，该值越大说明套保效果越好。通过计算，得到的结果如下：

我们利用3个不同的模型对应的最优套保比率得到了3种套期保值资产组合，套期保值后的收益率方差远远小于原来的收益率方差，这意味着我们的套期保值模型是有效的。而从上表中可以看出，这3中资产组合的套保效率非常接近，差异非常小，其中利用ECM模型得到的资产组合，套保效率略高于其他。

四、结论

本文选取了2015年整年的沪深300股票指数和沪深300股指期货的数据，进行建模分析，企图找到一种对冲方法，为股指基金管理者提供对冲系统性风险的策略。

在全样本数据分析过程中，本文分别用BVAR、ECM、GARCH模型找到了对应的最优套期保值比率，基金管理者只需要按此比率配置沪深300成分股和沪深300股指期货空头头寸，即可实现对系统性风险的对冲。并利用此比率，我们也得到了对应的对冲效率。结果发现，这三种模型实现的对冲策略的效果差异不大，经过对冲后的资产组合收益率的波动性远远小于沪深300指数收益率的波动性。

综上所述，本文所研究的策略并不能完全对冲系统性风险，套期保值的效率仅为80%左右，一个重要的原因可能是由于套期保值比率保持不变，没有根据市场实际情况随时调整。因此还有待于做更深入研究，找到更优的对冲策略。

参考文献：

［1］代军、朱新玲，沪深300股指期货对冲效率研究［J］.中国管理科学，2014

［2］谭海东，指数基金如何利用沪深300股指期货进行套期保值［J］.西南财经大学硕士论文，2011

［3］Park.T.H，Switzer.L.N，Time-varying Distributions and The Optimal Hedge Ratios for Stock Index Futures［J］.Applied Financial Economics，1995

［4］Myers.R.J，Estimating Time-Varying Optimal Hedge Ratios on Futures Markets［J］.The Journal of Futures Markets，1991