结蜡厚度对含蜡原油管道蜡沉积速率预测的影响
张莹
结蜡厚度对含蜡原油管道蜡沉积速率预测的影响
张莹
(中国石油大学(北京)油气管道输送安全国家工程实验室, 北京 102249)
以铁岭-秦皇岛管道冬季输送大庆原油为算例,对考虑和不考虑已有沉积物对后续沉积速率影响这两种算法通过MATLAB软件编程进行对比。结果表明,两种算法蜡沉积速率的差异与相对结蜡厚度成线性关系,相对结蜡厚度越大,差异越大。通过进一步计算分析,明确了造成两种算法差异的主要原因是动力参数的变化。
含蜡原油;结蜡厚度;蜡沉积速率;
我国原油多为含蜡原油,在管道输送过程中,溶解于油中的蜡分子会随着油流温度的降低而逐渐析出并沉积在管壁上,随着运行时间的延长,结蜡厚度越来越大,会造成管道内有效管径减小,造成输量降低、压力增大、输送成本增大等问题,故当结蜡厚度达到一定程度时就必须对管道进行清管。因此需要准确地判断结蜡速率,才能准确地对结蜡厚度做出预测,这对于输油管道安全、经济运行至关重要[1]。根据查阅的已有文献中,发现在对结蜡速率计算时有的文献考虑了已有的结蜡厚度对后续蜡沉积速率的影响,而有的文献并未提及上述影响,故本文希望通过就考虑和不考虑结蜡厚度对蜡沉积速率的影响做比较。
1 结蜡模型概述
国内外学者在研究结蜡规律时,一般先从蜡沉积机理分析入手,然后通过室内模拟实验,在获取实验数据的基础上,建立半理论半经验模型,再通过现场数据对模型检验,从而判定模型的适用性及准确性。结蜡模型主要分两类:一类是蜡析出模型[2-4],另一类是蜡沉积模型[5-7]。
本论文根据蜡沉积方面的已有成果,并以中国石油大学(北京)黄启玉[7]等人的普适性结蜡模型为核心基础,就考虑和不考虑结蜡厚度采用MATLAB软件编程对蜡沉积速率的影响这两种算法对蜡沉积结果进行计算。
2 计算介绍
2.1 结蜡模型
与前人的结蜡模型相比,普适性模型明确地考虑了管壁处剪切应力的影响,将一些确定及不确定因素归于值中。该模型的优点在于当其被用于现场结蜡预测时不需要通过大量的模拟实验并且经过验证,准确度较高。具体计算式为:
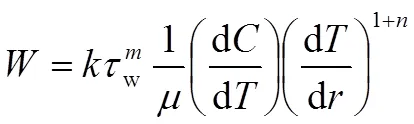

2.2 主要参数
(1)沿线油温
利用苏霍夫公式计算,本文中按1 km为一个步长单位,不足1 km的按1 km计算。
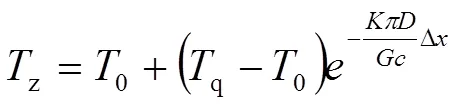
(2)管壁处径向温度梯度d/d
(3)管壁处剪切应力

表1 管壁处剪切应力
(4)管壁处蜡分子溶解度系数
运用DSC方法可以确定原油的含蜡量以及某一温度区内原油的析蜡量,根据原油的析蜡特性曲线(不同温度的累积析蜡量),得到平均油温下管壁处蜡分子溶解度系数。
(5)黏度、密度、比热容、导热系数
黏度:根据原油的黏温曲线得到对应温度下的黏度。
比热容:比热容是温度的函数,原油和成品油的比热容一般在1.6~2.5 kJ/(kg·℃),本文粗略计算时取2 150 J/(kg·℃)。
导热系数:本文粗略计算原油导热系数取0.14 W/(m·℃)。石蜡导热系数取2.5 W/(m·℃)。
(6)总传热系数
3 计算程序框图
计算程序见图1。
4 程序算例
以铁秦线铁岭—新民站间管段冬季输送大庆原油时为算例。
原油物性:大庆原油凝点33.5 ℃,析蜡点44.2 ℃,含蜡量28.44%,20 ℃时的密度为860 kg/m3。
选取距出站1 km(起点)、8 km(结蜡最严重的点)和92 km(终点)处的节点进行分析,实线代表不考虑结蜡厚度对蜡沉积速率的影响,虚线代表考虑结蜡厚度对蜡沉积速率的影响。

图1 考虑结蜡厚度对蜡沉积速率影响的程序框图
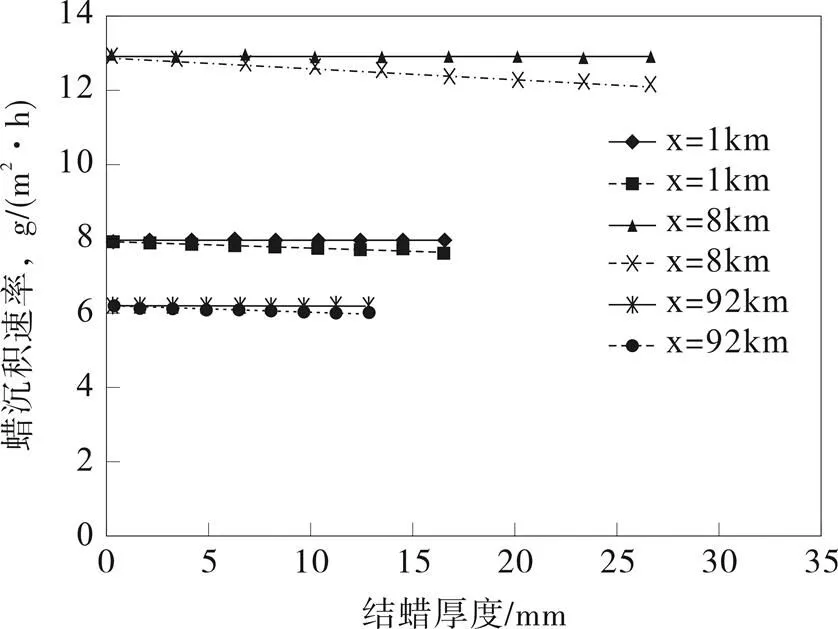
图2 不同节点处两种算法的蜡沉积速率
(1)不同节点处,考虑和不考虑结蜡厚度影响时,蜡沉积速率规律一致。即不考虑结蜡厚度影响时,蜡沉积速率不变;考虑结蜡厚度影响时,结蜡厚度越大,蜡沉积速率越小。
(2)同一节点处,在考虑结蜡厚度对传热影响时,结蜡厚度越大,蜡沉积速率减小得越快。因为考虑结蜡厚度时对传热影响时,结蜡厚度越大,总传热系数减小得越来越快,相当于形成的保温蜡层的保温效果越来越好,油流与外界换热受阻,同一节点处蜡层表面的温度升高得越来越快,径向温度梯度减小得越来越快,蜡分子扩散速率减慢,因此结蜡速率也因此随结蜡厚度增加而减小得越来越快。
为更加清楚地描述两种算法蜡沉积速率的差异,故定义了如下变量:
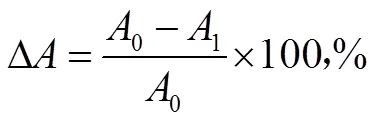
以=8 km处的节点为例,计算了该处两种算法蜡沉积速率差异、传热系数的差异、管壁处剪切力差异和温度梯度差异随结蜡厚度的变化情况,见图3(a)、图3(b)、图3(c)和图3(d)。

图3(a)~(d) 各参数的差异与结蜡厚度的关系
这是由于随着运行时间的延长,同一节点处的蜡层厚度不断增大,在考虑结蜡厚度对传热的影响时,该节点处的总传热系数和管内径也会不断减小,进而引起了蜡沉积速率计算公式中的径向温度梯度、管壁处剪切力等参数的变化。
5 结 论

[1]王平, 江国业, 田艺兵,等. 结蜡厚度对输油成本的影响[J]. 石油化工高等学校学报, 2002, 01: 47-50.
[2]Won K W. Thermo dynamics Calculation of Cloud Point Temperature and Wax Phase Composition of Refined Hydrocarbon Mixtures[J]. Fluid Phase Equil, 1989 (53).
[3]Hansen J H, Pedersen K S. Thermo dynamic Model for Predicting Wax Formation in Crude Oils[J]. AIChE: 1988 (34).
[4]Svendsen J A. Mathematical Modeling of Wax Deposition in Oil Pipeline Systems[J]. AIChE, 1993 (39).
[5]Burger E D., Perkins T K., Striegler J H. Studies of Wax Deposition in the Trans–Alaska Pipeline[J]. Journal of Petroleum Technology, 1981(4): 1075-1086.
[6]Hamouda A A, Ravn y J M. Prediction of Wax Deposition in Pipelines and Field Experience on the Influence of Wax on Drag-Reducer Performance, OTC 7060, the 24th Annual OTC, Houston, Texas, 1992, 669-679.
[7]黄启玉,李瑜仙,张劲军.普适性结蜡模型研究[J].石油学报, 2008, 03: 459-462.
Effect of Wax Deposit Thickness on Prediction of Wax Deposition Rate in Waxy Crude Oil Pipelines
(National Engineering Laboratory of Oil and Gas Pipeline Transportation Safety, China University of Petroleum, Beijing 102249,China)
Taking Tieling-Qinhuangdao pipeline for transporting Daqing crude oil in winter for an example, based on the mechanism of waxy crude wax deposition and wax deposition rate model, two kinds of algorithms: considering and without considering the impact of wax deposits on subsequent wax deposition rate, were developed; a comparison was carried out for calculating the wax deposition rate by using Matlab language. The results show that, in the pipeline transportation of waxy crude oil, the difference between wax deposition rates calculated by using two algorithms has a linear relationship with wax deposit thickness, the greater the relative wax deposit thickness, the greater the difference is. Furthermore, the computing results show that, the main factor to cause the difference of these two algorithms is the variation of the dynamic parameter.
waxy crude oil; wax deposition rate; pipeline transportation
TE 832
A
1004-0935(2017)04-0377-04
2017-03-06
张莹(1993-),女,中国石油大学(北京)研究生在读,湖北省荆州市人,2015 年毕业于中国石油大学(北京)油气储运工程专业, 研究方向:从事多相管流及油气田集输。

