蓄水坑灌苹果园冬季土壤温度分布动态预测模型
王晓磊,郭向红,孙西欢,2,马娟娟,雷 涛,曹 鹭
(1.太原理工大学水利科学与工程学院,太原,030024;2. 晋中学院,山西 晋中 030600)
0 引 言
蓄水坑灌法是一种具有节水、保水、抗旱和诱导根系深扎等优点的果林节水灌溉方法[1,2]。该灌溉方法是在距树干一定距离处均匀布置若干小蓄水坑,灌溉时可通过管道将水注入坑内,水分沿坑壁渗入根区土壤,从而促进根系对水分的吸收。与地面灌溉相比,蓄水坑灌土壤水分在40~160 cm处土壤含水率较大,这将更有利于根系对土壤水分的吸收[3]。同时,蓄水坑的存在增加了根区中深层土壤与空气的接触面,使冬季坑壁附近的中深层土壤温度明显小于地面灌溉处理,这可能会造成果树生长速度减慢,甚至出现冻害现象。为此,李俊杰[4]和张亚琼[5]分别对不同坑口直径和不同覆盖方式下的土壤温度分布特性进行了研究,结果表明:蓄水坑内土壤温度随坑口直径的减小而减小。不同覆盖条件下的蓄水坑增温效果表现为:地膜覆盖>秸秆覆盖>无覆盖。目前,蓄水坑灌冬季土壤温度研究多集中于定性的试验研究[4,5],相关的定量计算研究相对较少,还有待进一步深入。开展对蓄水坑灌冬季土壤日际变化最低温度的预测研究不仅可以丰富蓄水坑灌的研究内容,还可以指导人们采取合理的措施避免冻害的发生。
土壤温度预测模型主要包括确定性和非确定性两种模型[6],其中,确定性模型主要是指基于土壤温度传热方程等所建立的数学模型。它可以较准确地对研究内容进行预测[7],但其数学方程式和所需参数较复杂。非确定性模型是指依赖于实测数据,通过人工智能算法而建立的灰色或黑色模型,相对确定性模型而言,其模型结构简单,参数较少,因此在实际中得到广泛应用。常见的非确定性模型主要包括BP神经网络,RBF神经网络和最小二乘向量机等。目前,相对RBF和最小二乘向量机模型而言,BP神经网络模型具有自学习能力和一定推广能力的优点,因此,在表土层土壤温度时间动态[6]、一维土柱水热动态变化[8]和土壤温度的变化特征及其预报模型[9]等预测方面得到广泛应用,取得了较好的模拟效果,证实了BP方法在土壤温度预测方面的稳定性和可靠性。因此,采用BP方法进行蓄水坑灌冬季土壤温度预测具有一定的合理性和可行性。本文将采用BP神经网络模型,实现蓄水坑灌冬季土壤温度的动态预测,以期为蓄水坑灌土壤温度定量研究提供有效工具。
1 材料及方法
1.1 试验区概况
试验于2015年11月28日-2016年3月15日和2016年11月28日-2017年3月15日在山西省太谷县果树所(地理坐标:东经112°32′,北纬37°23′)内进行,试验地平均海拔约800 m,属暖温带大陆半干旱气候。试验区土壤以粉砂壤土和壤土为主,试验期间,冬季平均气温约2.7 ℃,降雨量约9.2 mm。试验对象为红富士矮砧苹果树。
1.2 试验设计及项目测定
本试验主要进行冬季蓄水坑灌条件下土壤温度时空分布预测研究。试验周期为2015年11月28日-2016年3月15日和2016年11月28日-2017年3月15日,试验累积观测217 d。图1为蓄水坑灌田间工程布置示意图。如图1所示,在距树干60 cm径向位置处均匀布置4个圆柱形坑,其坑口直径30 cm,坑深40 cm。根据田间实际情况,对土壤温度测点进行合理的布置。在径向,以距蓄水坑壁5、15、25、35 cm处布点。在垂向,以距地表10、20、30、40、50、60、70、80 cm处布点。此外,在距蓄水坑壁25 cm处的地表布置一个测点,对地表温度进行监测。土壤温度采用HZR-8T型温度自动测量仪进行测定,精度为0.1 ℃,采集频率为30 min。
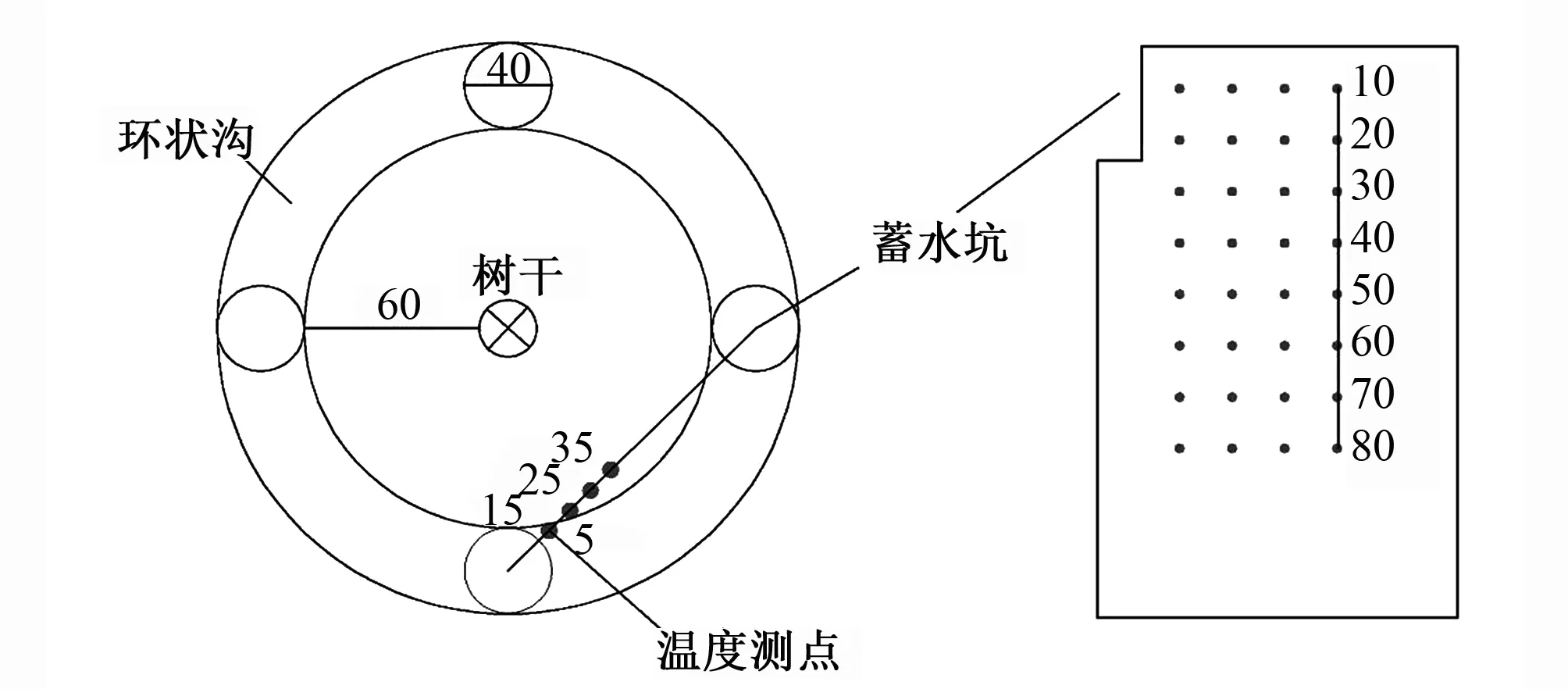
图1 蓄水坑灌田间工程布置示意图(单位:cm)Fig.1 Survey of arrangement of water storage pit irrigation
1.3 数据处理及模型评价
试验原始数据采用Microsoft Office 2013进行整理;采用MATLAB 2016 软件进行BP神经网络模型的训练和验证;采用Origin 9.1软件进行分析绘图;采用平均相对误差MAPE指标对模型精度进行评价。公式为:
(1)
式中:Zy为BP神经网络的预测值;Zs为实测值;N为样本数量。
2 模型构建
2.1 BP神经网络原理
BP神经网络是一种解决复杂的高维非线性问题的有效方法。BP神经网络主要包含三层:输入层、隐含层和输出层。这些神经网络层的作用分别为接收信息、处理信息和传输信息。当输出层结果与期望值不一致时,误差反向传播机制启动,对各层的权值和阈值信息进行不断调整,直到满足精度要求为止。BP神经网络的预测步骤[10]主要包括:①输入层和输出层神经元数目、训练函数、学习速度和传递函数等网络参数的初始化。②训练样本和预测试样本的选择。③通过对网络权值和阈值的多次修正,使模型达到训练要求。④将预测组样本带入训练好的模型,得到预测组样本的预测值。⑤分析、评价预测结果。
2.2 模型构建
土壤热传递主要包括3种方式:传导、对流和辐射。太阳的热辐射作用会引起地表土壤温度的升高,导致上层土壤与下层土壤之间形成明显的温度势梯度,为土壤间的热传导作用提供了主要动力。地表温度高低是太阳热辐射作用强度大小的直接表现,是决定土壤温度垂向传递强度的诱因。太阳的热辐射还会引起大气温度的上升,在热对流作用和温度势梯度作用下,地表大气与坑内大气发生热交换,导致坑内温度升高,坑内大气又持续将热量沿蓄水坑壁传递给土壤层,引起土壤温度发生变化。蓄水坑内温度高低是热量沿坑壁发生侧向传导作用的诱因。当热量进入土体后,此时的热传递行为将主要取决于土壤本身,某特征位置处的土壤温度高低是决定自身吸放热行为的重要因素。因此,本文将地表平均温度、坑内平均温度和距离坑壁5 cm处的各层土壤温度(共8层)作为模型的输入项。模型的输出项为距离坑壁15、25和35 cm处的各层土壤温度,即土壤温度的空间分布。因此,BP神经网络模型的输入节点为11,输出层节点为8。此时,模型构建的关键在于确定隐含层节点数。通常,BP神经网络模型的精度与隐含层节点数目紧密相关,节点数目过高或者过低,均会引起模型精度的下降。本文首先通过经验公式法[式(2)]对隐含层节点数的合理范围进行确定,然后结合试算法对最优节点数进行确定[11]。经过多次试算,确定模型最优节点数为13。因此,本文构建的蓄水坑灌土壤温度预测模型(BP-WSPI-T)的最优拓扑结构为11-13-8,模型基本构架如图2所示。
(2)
式中:p为隐含层节点数;r为输入层节点数;c为输出层节点数;n为经验值(1≤n≤10)。
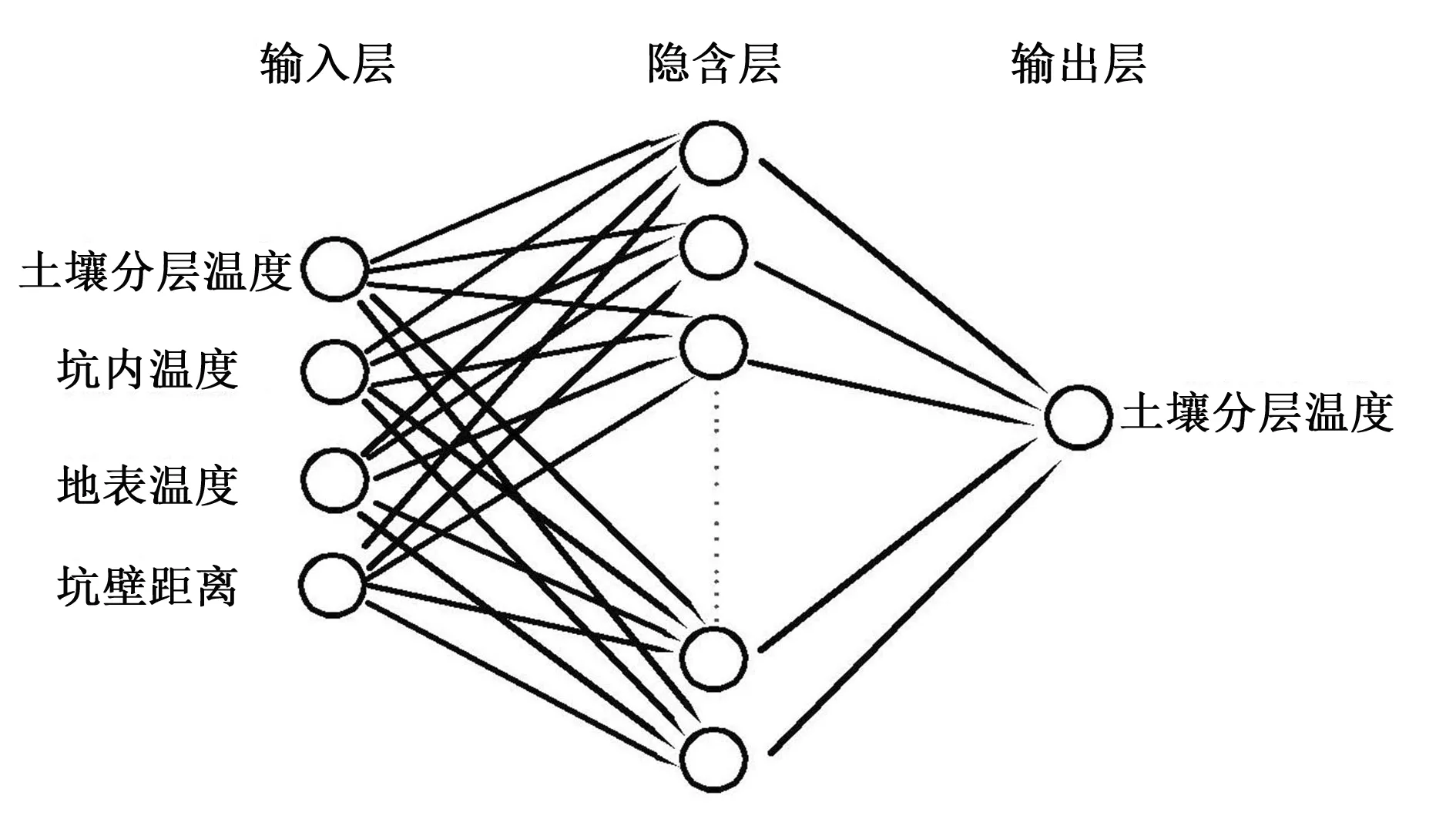
图2 土壤温度动态变化的BP神经网络模型结构示意图Fig.2 Structural model of BP neural network model with dynamic change of soil temperature
2.3 样本选择
本研究累积试验周期为217 d,其中2015年109 d,2016年108 d。试验期间,每天可获得1组数据样本。因此,样本总数为217组。选取前174 d的数据为训练集,后43 d的数据为训练集,得到训练集数据共174组,预测集数据共43组。表1为训练样本与预测样本的统计学特征值。
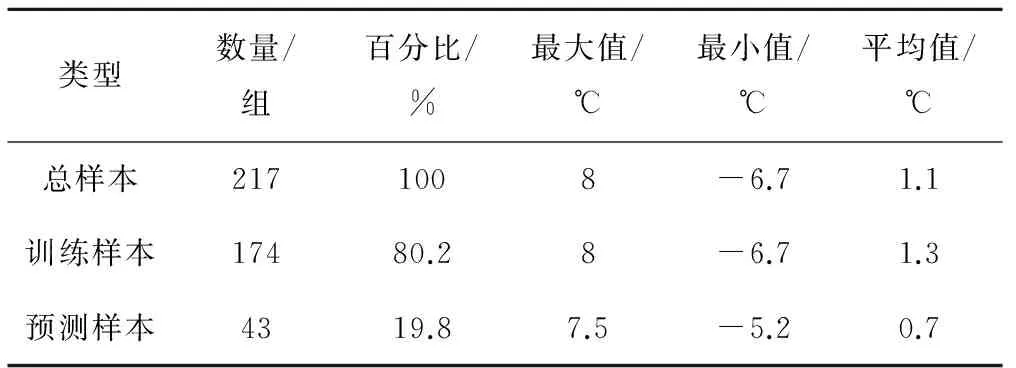
表1 训练样本与预测样本统计学特征值Tab.1 Statistical characteristics of training samplesand predictive samples
3 结果与分析
3.1 训练集结果分析
为评价BP-WSPI-T模型的训练效果,对训练组样本实测值与预测值的线性一致性和统计学差异进行分析。图3为训练组样本实测值与预测值间的线性关系。由图3可知,距坑壁15、25和35 cm位置处的土壤温度预测值和实测值构成的线性方程的斜率分别为0.988 7、0.994 7和0.982 7,决定系数R2分别为0.984 1和0.987 5和0.979 6,说明模型预测值与实测值具有较好的一致性。表2为实测值与预测值差异性统计结果。由表2可知,对距坑壁15、25和35 cm特征位置处实测值与预测值进行统计学分析时,t值绝对值分别为0.460、0.545和0.323,均小于t检验临界值,即t0.05(1 391)=1.645。由此可知,训练组样本预测值与实测值间的差异未达到显著水平。BP-WSPI-T模型训练效果较好,可以用于冬季土壤最低温度的预测。
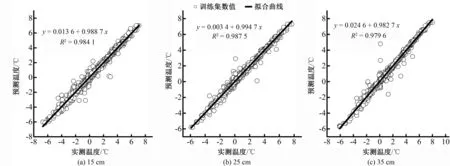
图3 训练组样本实测值与预测值间的线性关系Fig.3 Linear consistency analysis of measured values and predictive values of soil minimum temperature in training group

坑壁距离/cm自由度P值t值1513910.645-0.4602513910.5860.5453513910.747-0.323
3.2 预测集结果分析
通过对模型进行训练,便可以获得模型的最优权值和阈值信息。将预测组数据带入训练好的模型,便可得到预测结果,对土壤最低温度实测值与预测值分布进行线性一致性分析及差异性统计结果检验。图4为线性一致性分析结果,从线性一致性结果可知:预测集中坑壁距离为15、25和35 cm的土壤温度预测值和实测值分布的斜率分别为0.983 2、0.954 2和0.977 0,决定系数R2分别为0.957 6和0.954 2和0.981 7,其线性相关程度较好。表3为实测值与预测值差异性统计结果,从差异性统计结果可知坑壁距离为15、25、35 cm的土壤温度分布的t值绝对值分别为0.600、0.985和0.464,均小于t临界值t0.05(863)=1.645,p>0.05。由此可知,预测组中不同坑壁距离的土壤最低温度预测值与实测值分布之间的差异均未达到显著水平,模型训练效果较好。经计算,坑壁距离为15、25、35 cm的BP-WSPI-T模型平均相对误差分别为8.7%、9.4%、7.3%,模型度预测精度均较高。因此,BP-WSPI-T模型具有较好的预测效果。
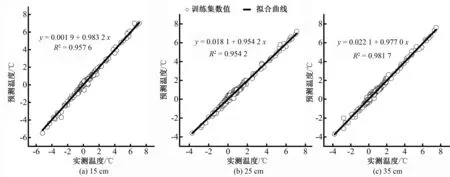
图4 预测组样本实测值与预测值间的线性关系Fig.4 The linear relationship between the measured value and the predicted value of the predicted group
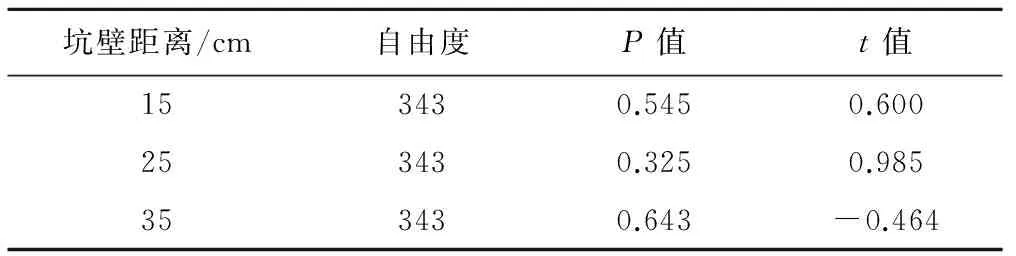
坑壁距离/cm自由度P值t值153430.5450.600253430.3250.985353430.643-0.464
为了进一步揭示BP-WSPI-T模型在蓄水坑冬季温度二维空间分布的预测效果,选取了2017年2月8日、2月18日和2月28日的土壤剖面温度,对模型预测值与实测值间的差异进行了比较,结果如图5所示。
由图5可知,土壤最低温度实测值与模型预测值在不同径向和垂向上的变化及分布趋势基本一致。经计算,三个典型剖面的预测精度分别为8.6%、7.4%和9.5%,总体精度为8.5%。由此可以说明,BP-WSPI-T模型在蓄水坑灌冬季土壤温度二维空间分布预测方面具有较好的预测效果。
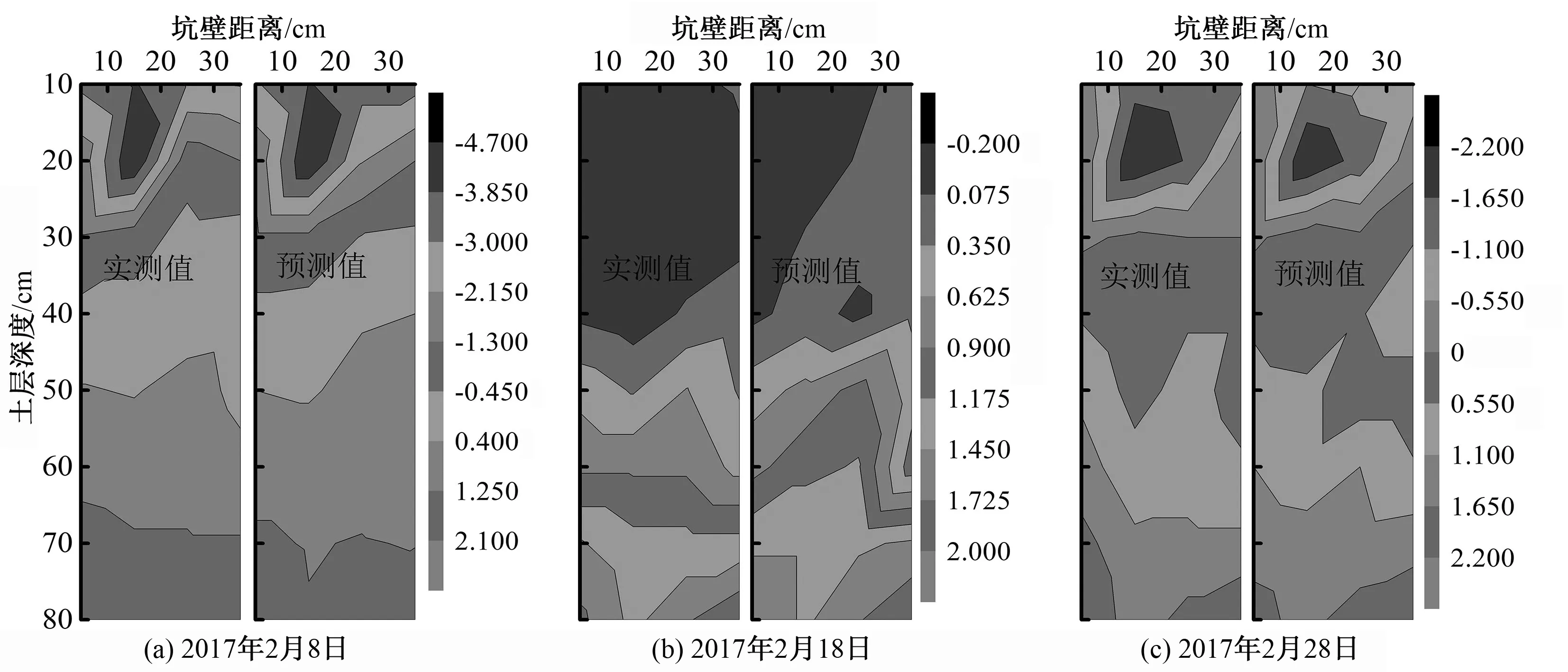
图5 土壤最低温度实测值与预测值二维分布比较Fig.5 Two - Dimensional distribution of measured values and predictive values of soil minimum temperature
4 结 论
本文以蓄水坑灌冬季土壤温度实测资料为基础,建立了以距蓄水坑壁5 cm处的分层土壤最低温度、坑内平均温度、地表温度和沿坑壁的径向距离为输入,以距蓄水坑壁15、25和35 cm处分层土壤最低温度为输出,拓扑关系为11-13-8的BP-WSPI-T模型。在对距坑壁15、25和35 cm处土壤最低温度进行预测时,BP-WSPI-T模型的平均相对误差分别为8.7%、9.4%、7.3%;对土壤温度空间二维分布进行预测时,模型平均相对误差为8.5%。因此,BP-WSPI-T模型可较好的模拟蓄水坑灌冬季土壤温度分布的动态变化,可为蓄水坑灌冬季土壤温度预测提供定量分析工具。
[1] 孙西欢.蓄水坑灌法及其水土保持作用仁[J]. 水土保持学报,2002,11(3):130-131.
[2] 孙西欢.蓄水坑灌法技术要素初探[J]. 沈阳农业大学学报,2004,25(5-6):405-407.
[3] 樊晓波,孙西欢,郭向红,等.蓄水坑灌土壤水分分布特征研究[J].中国农村水利水电,2013,(3):69-72.
[4] 李俊杰.蓄水坑灌不同蓄水坑结构型式条件下果园冬季土壤温度分布特征研究[D]. 太原:太原理工大学,2015.
[5] 张亚琼.不同覆盖方式下蓄水坑土壤温度变化特征研究[D]. 太原:太原理工大学,2013.
[6] 邹 平,杨劲松,姚荣江.土壤温度时间序列预测的BP神经网络模型研究[J]. 中国生态农业学报,2008,(4):835-838.
[7] 赵二岭.几类确定性网络模型的特性研究[D]. 西宁:青海师范大学,2013.
[8] 王宏宇,马娟娟,孙西欢,等. 基于BP神经网络的土壤水热动态预测模型研究[J].节水灌溉,2017,(7):11-15,27.
[9] 王选耀.烟台地区土壤温度变化特征及预测模型研究[J].农业系统科学与综合研究,2010,26(4):487-492.
[10] 吴 渊.基于BP神经网络的车载设备故障诊断与预测研究[D]. 北京:北京交通大学,2016.
[11] Wang J, Huang J, Wu P, Zhao X. Application of neural network and grey relational analysis in ranking the factors affecting runoff and sediment yield under simulated rainfall [J]. Soil Research, 2016,54(3):291-301.

