递归神经网络在降雨量预测中的应用研究

张 帅，魏正英，张育斌

(西安交通大学机械制造系统工程国家重点实验室，西安 710054)

我国是一个干旱缺水的国家，淡水资源非常有限且分布极不均衡，水资源是制约社会经济发展和生态环境改善的主要因素[1]。我国西北地区农业用水大多都是依靠自然降雨，降雨量对农业生产有着重要的影响，因此对可利用降雨量的预测对于农业灌溉用水管理有着非常重要的作用。

由于气象参数之间高度复杂的相互作用，降雨量存在不确定性与随机性，因此降雨量预测是一个严峻的任务。目前，国内外有关降雨量预测方法有很多，主要有概率统计法、灰色预测方法、马尔科夫链、时间序列法等，这些技术模型都获得了一定的准确率，概率统计法、灰色预测方法、马尔科夫链比较适合降雨量呈指数型增长的数据，时间序列法预测值比较趋于平均值[2-4]。然而在实际生活中降雨量是一种具有随机波动的数据集合，数据不一定呈指数型规律增长，这些模型仅限于固定长度的序列信息，没有充分考虑降雨量变化的时间序列属性，所以预测精度不高[5]。

递归神经网络是一类人工神经网络，用于识别诸如文本、语音等序列数据的模式或者识别传感器、股票市场产生的数值型时间序列数据[6]。递归神经网络充分考虑了时间序列的动态特性，通过对网络的学习提高了自学习自适应能力，使其能够更好地处理序列数据。本文将递归神经网络模型应用到降雨量预测中指导农业灌溉，并且利用其他3种网络模型进行实验对比。

1 模型原理

1.1 递归神经网络

递归神经网络是一类由各单位之间连接形成的有向循环的人工神经网络，这是前馈神经网络在处理序列数据的自然延伸，所不同的是，其输入不仅包括当前所见的输入样例，还包括网络在上一个时刻所感知到的信息[7]。利用这一性质，信息可以在网络内部循环任意长的时间。如图1所示, 标准网络包含3个层，输入层、隐藏层和输出层。

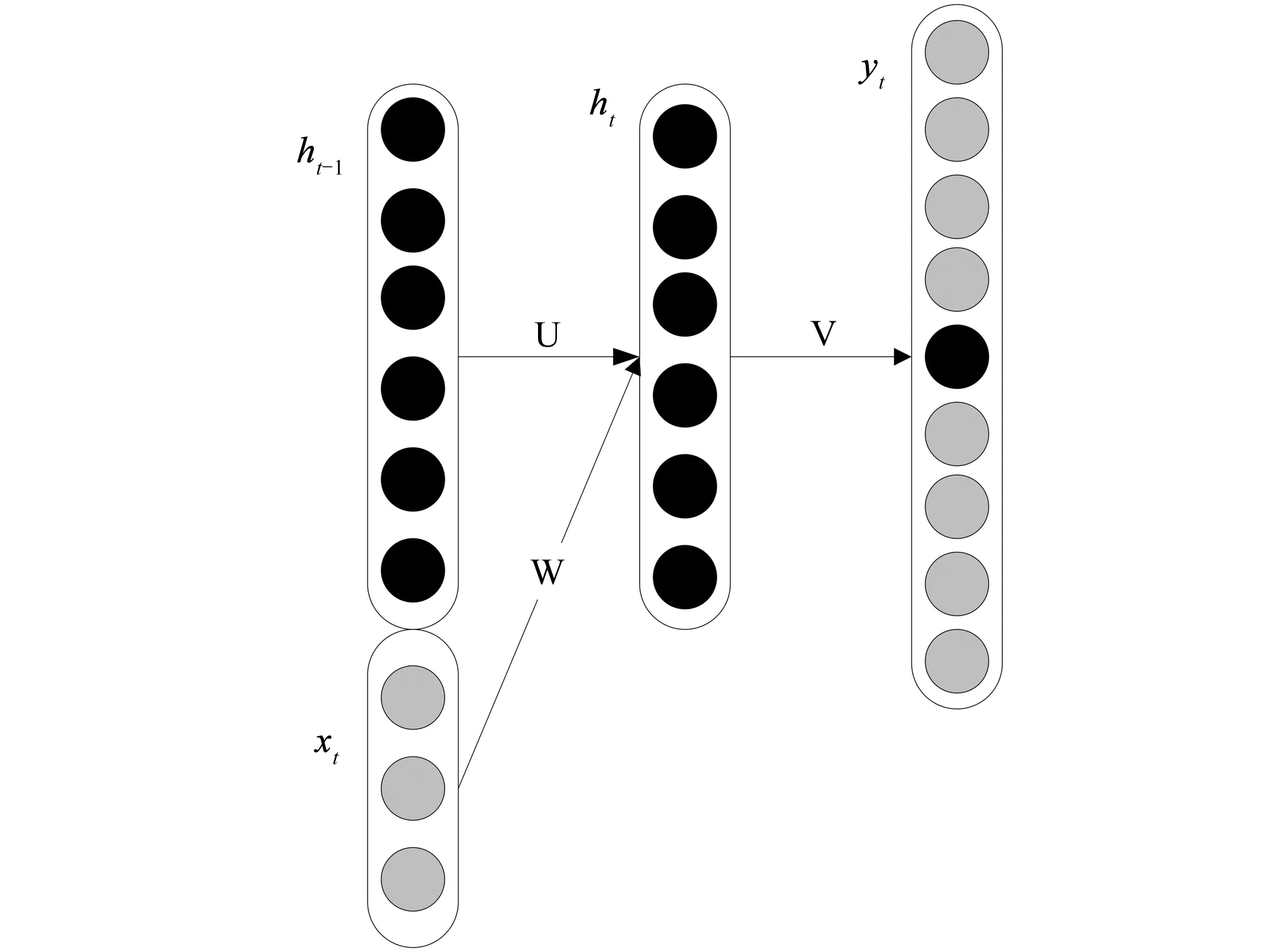
图1 递归神经网络Fig.1 Recurrent neural network

工作过程如下：给定输入向量序列(x1,…,xT)，计算隐状态的一个序列(h1,…,hT)，通过迭代下列公式计算t=1至t=T的输出序列(Y1,…,YT)[8,9]：

ht=tanh(Whxxt+Whhht-1+bh)

(1)

yt=Wohht+bo

(2)

式中：Whx是输入层到隐藏层的权重矩阵；Whh是隐藏层到隐藏层的权重矩阵；Woh是隐藏层到输出层权重矩阵；bh和bo是偏值；输入层是ht-1和xt；ht-1是从初始时刻到t-1的串联的历史信息；xt是t时刻输入层的序列，它与以前的历史信息ht-1结合产生当前的隐含层ht，基于ht可以预测下一时刻yt。

1.2 长短期记忆

长短期记忆单元由德国学者Sepp Hochreiter和Juergen Schmidhuber于20世纪90年代中期提出，由一组名为记忆块的特殊单元组成，这些记忆块可以记住隐藏层的任意时间状态，从而解决梯度消失的问题[10]。长短期记忆单元可将误差保持在更为恒定的水平，用于沿时间和层进行反向传递，让递归网络能够进行许多个时间步的学习，从而打开建立远距离因果联系的通道[11]。

一个记忆块主要由4个部分组成：输入门、自连接的神经元、忘记门和输出门(如图2所示)，这些门用于调制存贮单元本身和环境之间的相互作用，这样从一个时刻到另一个时刻，存储单元的状态可以保持不变[12]。LSTM将信息存放在递归网络正常信息流之外的门控单元中，单元通过门的开关判定存储哪些信息，以及何时允许读取、写入或删除信息[13]。LSTM网络通过递归使用方程[14]更新网络单元，激活从输入序列x到输出序列y的映射:

图2 长短期记忆单元Fig.2 LSTM memory cell

it=σ(Wixxt+Wimmt-1+Wicct-1+bi)

(3)

ft=σ(Wfxxt+Wmfmt-1+Wcfct-1+bf)

(4)

ct=ftΘct-1+itΘg(Wcxxt+Wcmmt-1+bc)

(5)

ot=σ(Woxxt+Wommt-1+Wocct+bo)

(6)

mt=otΘh(ct)

(7)

yt=Wymmt+by

(8)

式中：σ是激活函数；i,f,o和c分别表示输入门、忘记门、输出门和单元激活向量；m表示t时刻激活函数作用之后单元的值；W表示权重矩阵；b表示偏值矩阵；Wix是输入门和输入之间的权重；bi是输入门偏值；Θ是矢量的逐元素乘积；g和h分别是单元输入和输出激活函数。

1.3 通过时间反向传播

通过时间反向传播可以看作是对经典反向传播算法的一种延伸，如图3所示，其基本原理就是通过叠加之前权值保留误差从而通过时间展开递归网络[15]，误差可被进一步反向传播。误差后向传播公式[16]如下：

δpj(t-1)=∑δph(t)uhjf′[spj(t-1)]

(9)

式中：h是t时间步长时隐藏节点的索引；j是t-1时间步长时隐藏节点的索引。

当获得所有的误差增量后，权重折回加起来更新每个展开的权重。BPTT往往比一般的优化技术如进化优化训练网络更快。

图3 通过时间反向传播Fig.3 Back-propagation through time

2 实验仿真

2.1 数据集

本文的数据是从中国气象数据共享服务网获得的榆林市气象站降雨量，数据包括2000-2013年的降雨量，如图4所示。数据包含年降雨量、月降雨量和旬降雨量，对于农业灌溉来说旬降雨量数据的重要性相对大于年度和月度降雨量数据，旬降雨量波动性更大，周期性更明显，所以本文选用旬降雨量为实验数据进行建模分析。

图4 2000-2013年降雨量Fig.4 Precipitation from 2000 to 2013

本研究将数据集分为训练集和测试集，数据集的统计结果如表1所示，表1中mean、std、min、max和median分别表示平均值、标准差、最小值、最大值和中位数。从图4和表1可以看出，降雨量是动态的、高变异的时间序列，数据呈散点分布，旬降雨量具有一定的周期性。

表1 数据集统计 mm

2.2 模型训练和评价指标

隐藏层的大小应该反映训练数据量，通常是30～500，在本文中选择300。训练网络前，权重初始化为很小的值，学习速率设置为0.001。实验中其他参数保持不变，对于每一个序列运用BPTT计算误差梯度，更新权重系数。当模型精度没有显著提高时，训练终止，通常20～50次迭代之后模型收敛。

为了评价模型的精度，本文运用均方根误差(RMSE)、平均绝对误差(MAE)，Nash-Sutcliffe系数(NS)[17]。RMSE、MAE和NS公式如下：

(12)

式中：pt是预测值；yt是对应目标值。

RMSE、MAE越小，NS系数越高，模型越好。

3 结果分析

本文选取3种不同输入序列，前9个序列数据、前18个序列数据和前36个序列数据，运用模型分别对训练集和测试集进行试验，模型的评价指标RMSE、MAE和NS结果如表2所示。

表2 RNN模型的RMSE、MAE、NS统计Tab.2 The RMSE,MAE and NS statistics of RNN

从表2中可以看出，输入数据和目标数据之间存在明确的关系。输入的序列数据越大，模型的精度越高。

图5和图6分别给出了最好的训练数据和测试数据结果，其中绿线表示真实值，蓝线为预测值。观察值和预测值是非常接近，同时趋势具有非常高的相似性，模型对极值点、降雨量出现较大波动处也有较好的拟合。

图5 递归神经网络对训练集的预测结果Fig.5 Predictions of RNN for training dataset

图6 递归神经网络对测试集的预测结果Fig.6 Predictions of RNN for test dataset

为比较模型，运用前馈神经网络模型、小波神经网络模型和ARIMA模型分别进行了实验对比，结果如图7～图12所示。

图7 前馈神经网络对训练集的预测结果Fig.7 Predictions of FNN for training dataset

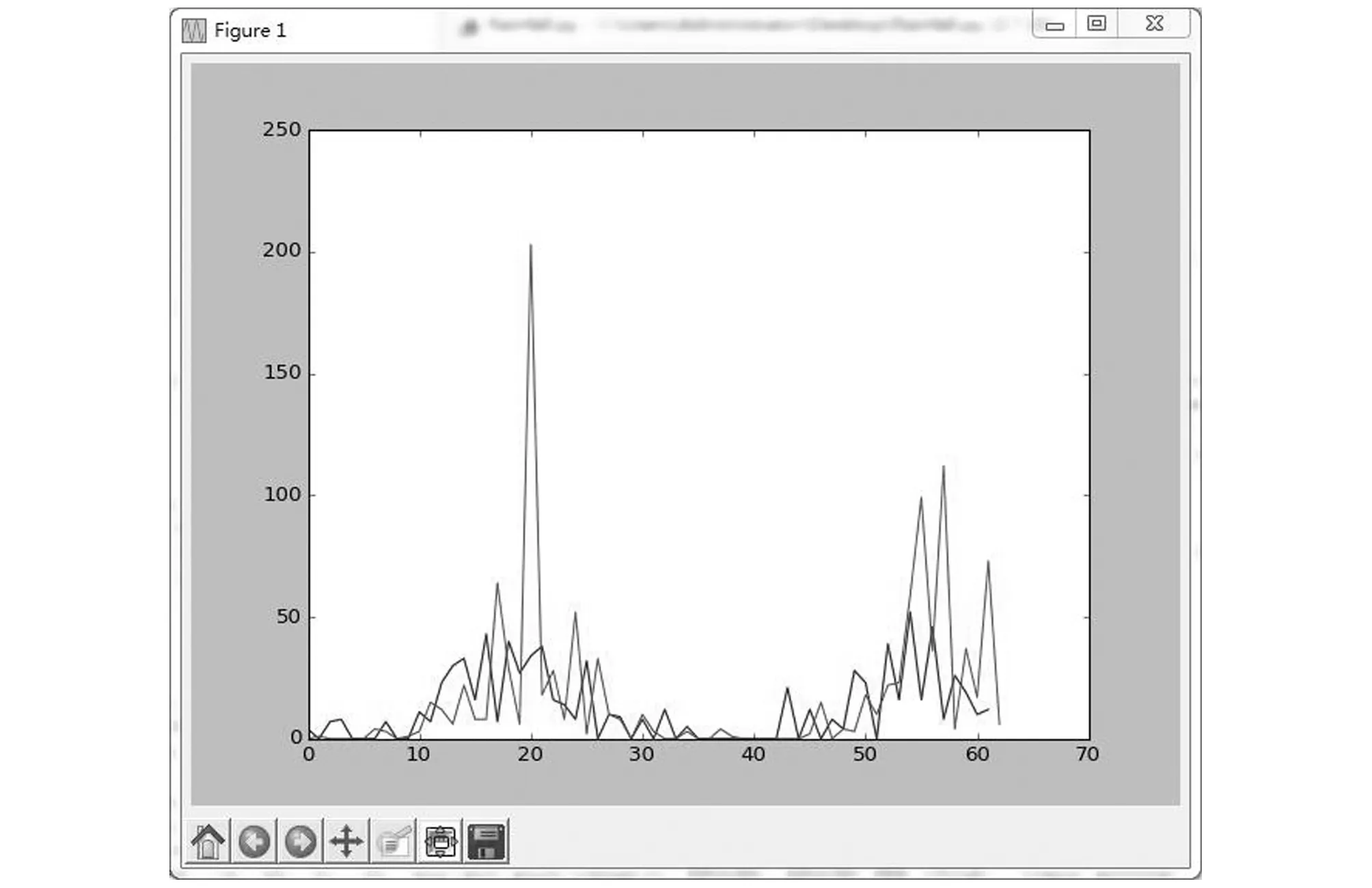
图8 前馈神经网络对测试集的预测结果Fig.8 Predictions of FNN for test dataset

图9 小波神经网络对训练集的预测结果Fig.9 Predictions of WNN for training dataset

图10 小波神经网络对测试集的预测结果Fig.10 Predictions of WNN for test dataset

图11 ARIMA对训练集的预测结果Fig.11 Predictions of ARIMA for training dataset

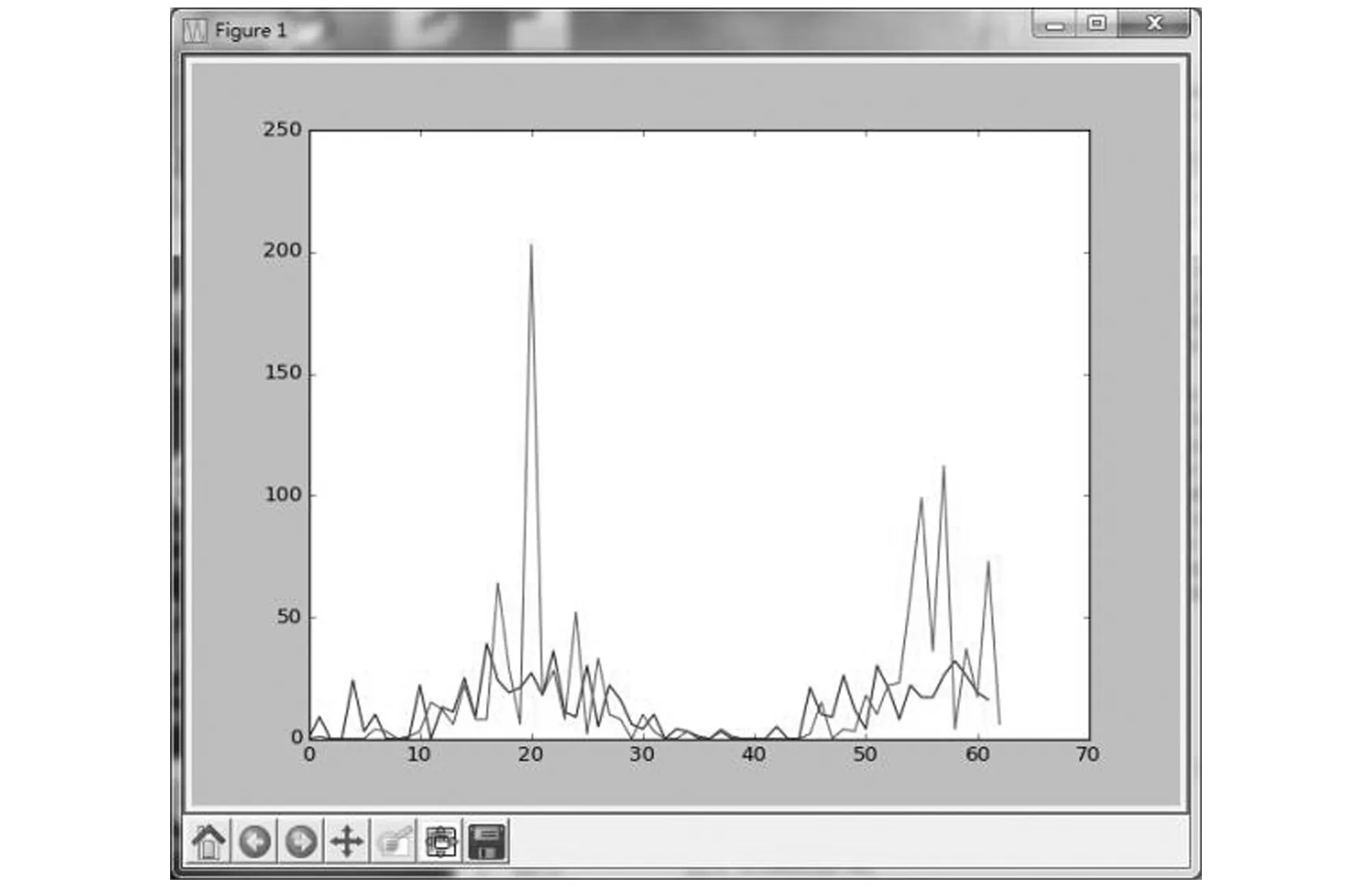
图12 ARIMA对测试集的预测结果Fig.12 Predictions of ARIMA for test dataset

表3显示了4个网络模型的性能概要。由上述结果可以看出，4种模型预测趋势与实际降雨量趋势基本一致，递归神经网络模型预测误差最小，ARIMA模型预测误差最大。相比其他模型，递归神经网络模型各种性能指标均优于其他模型，说明递归神经网络模型能够更好地描述降雨量的动态、非线性变化规律，模型性能更好，适用于降雨量时间序列建模。

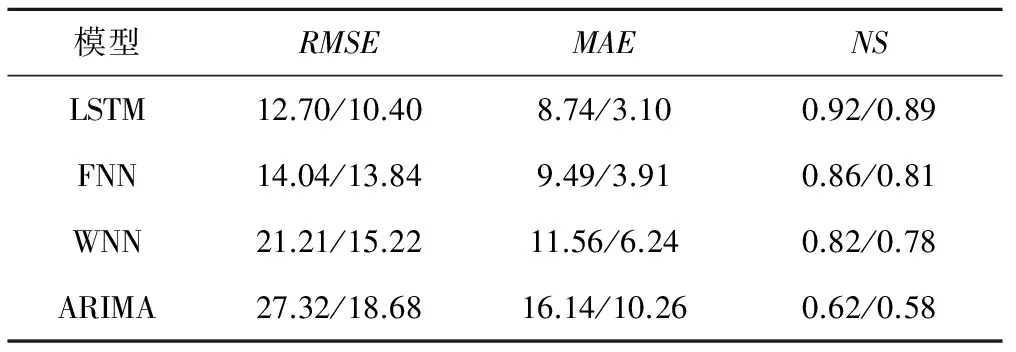
表3 不同模型性能比较Tab.3 different model performance comparison

注：“/”左边为训练集数据，右边为测试集数据。

4 结 语

本文以降雨量预测为具体实例，构建了基于递归神经网络的降雨量预测模型，以榆林市降雨量数据进行预测分析，结果表明模型预测精度高、泛化能力好、误差较小， 能够有效地预测降雨量，对农业用水管理、合理制定灌溉制度具有一定的参考意义。

递归神经网络适合序列建模任务,相对于以前的方法,它不受传统神经网络训练问题干扰，较好地解决了高维数、非线性和局部极小问题。带有长短期记忆单元的递归神经网络比其他模型更健壮，BPTT算法比其他方法训练更快,也更准确。相比其他3个模型，递归神经网络模型表现更优异。

[1] 张 强,赵映东.西北干旱区水循环与水资源问题[J].干旱气象,2008,26(2):1-8.

[2] Nirmala M, Sundaram S M. A seasonal ARIMA model for forecasting monthly rainfall in Tamilnadu[J]. National Journal on Advances in Building Sciences and Mechanics, 2010,1(2).

[3] Ozgur Kisi, Mesut Cimen.Precipitation forecasting by using wavelet-support vector machine conjunction model[J]. Engineering Applications of Artificial Intelligence,2012,25:783-792.

[4] 常 青,赵晓莉.时间序列模型在降水量预测中的应用研究[J〗.计算机仿真,2011,28(7):204-206．

[5] 陶 猛，徐淑琴.时间序列小波神经网络组合模型在年降雨量预测中的应用[J].节水灌溉,2013,(12):40-45.

[6] Tomas Mikolov,Martin Karafit, Lukas Burget, et al.Recurrent neural network based language model[C]∥ Eleventh annual conference of the international speech communication association. 2010:1 045-1 048.

[7] Mikael Bodén. A guide to recurrent neural networks and backpropagation[Z],2001.

[8] Alex Graves,Navdeep Jaitly. Towards end-to-end speech recognition with recurrent neural networks[C]∥ Proceedings of the 31 st international conference on machine learning. Beijing, China, JMLR: W&CP, 2014:32.

[9] Shujie Liu, Nan Yang, Mu Li, et al. A recursive recurrent neural network for statistical machine translation[C]∥Proceedings of the 52nd annual meeting of the association for computational linguistics. 2014:1 491-1 500.

[10] S Hochreiter, J Schmidhuber. Long short-term memory[J]. Neural Computation, 1997,9(8):1 735-1 780.

[11] Hochreiter, Y Bengio, P Frasconi, et al. A field guide to dynamical recurrent neural networks[R]. IEEE Press, 2001.

[12] Felix A Gers, Jurgen Schmidhuber,Fred Cummins. Learning to forget: continual prediction with LSTM[C]∥ Technical Report IDSIA-01-99. 1999.

[13] Alex Graves. Supervised sequence labelling with recurrent neural networks[Z]. 2008:31-38.

[14] Hasim Sak, Andrew Senior, Françoise Beaufays. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition[R]. 2014.

[15] Herbert Jaeger. A tutorial on training recurrent neural networks covering BPPT,RTRL,EKF and the “echo state network” approach[R]. 2013.

[16] Werbos P J. Back propagation through time: what it is and how to do it[J].Proceedings of the IEEE, 1990,78(10):1 550-1 560.

[17] J E Nash, J V Sutcliffe. River flow forecasting through conceptual models part I ---- a discussion of principles[J]. Journal of Hydrology,1970,10(3):282-290.