水肥混合液浓度检测交叉敏感抑制的研究

张 磊，魏正英，张育斌，简 宁

(西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

随着技术的快速发展，离子选择电极的出现逐步代替了EC电极在水肥混合液成分浓度的检测，降低了综合指数的模糊指导，通过针对相应离子的选择电极得到精确的浓度值。然而，离子选择电极在多组分检测中，掺杂离子会对其输出值产生影响，这种交叉敏感现象的存在对测量精度造成较大的偏差[1,2]。为了解决该问题，研究人员提出了很多交叉敏感抑制的方法。硬件方面：改进离子选择电极的结构、增加材料涂层来提高检测离子的通过率阻止掺杂离子的干扰通过率；软件方面：应用数值计算方法和神经网络算法对检测结果进行修正。因为硬件的研制成本较高、周期较长，软件的方法受到了极大的关注。Andrey Legin等[3]检测血液中离子浓度数据源，运用BP神经网络来消除交叉敏感的影响；周东祥等[4]针对气敏传感器交叉敏感现象，使用BP人工神经网络来抑制该问题；简宁等[5]采用遗传优化BP神经网络的方法来建立交叉敏感模型。然而BP神经网络算法[6]需要大量的训练样本，训练时间较长，不能很好地解决传感器的交叉敏感。

鉴于以上因素，本文应用支持向量回归算法，寻找最优参数，获得回归拟合模型，降低离子选择电极交叉敏感现象，提高检测精确度。

1 离子选择电极概述

离子选择电极[7,8](Ion Selective Electrode，简称ISE)是一种分析溶液离子浓度的工具，主要结构包括工作电极、参比电极和敏感膜等。

通过敏感膜和溶液在相界面上产生与待测离子活度有关的膜电势，电极膜的电位与待测离子含量之间的关系满足能斯特(Nernst)方程[9]如下所示。

(1)

式中：EM为离子选择电极在热力学温度T时的输出电势；Eind为工作电极输出电势；Eref为参比电极输出电势；E0为离子选择电极标准输出电势；R为摩尔气体常数；T为热力学绝对温度；zi为待测离子电荷数；F为法拉第常数；αi为待测离子浓度。

从公式中可以看出输出电势EM和离子浓度αi对数值成线性相关。因此通过测量离子选择电极的响应电势就能获得相应离子的浓度。

从图1可以看出，离子选择电极的响应电势，是以参比电极作为基准电势，与电解溶液的电解电势、敏感膜感应电势、内充液电势、工作电极内金属丝的电势、测量仪器导线上产生的电势一一比较，得到电极的响应电势值。

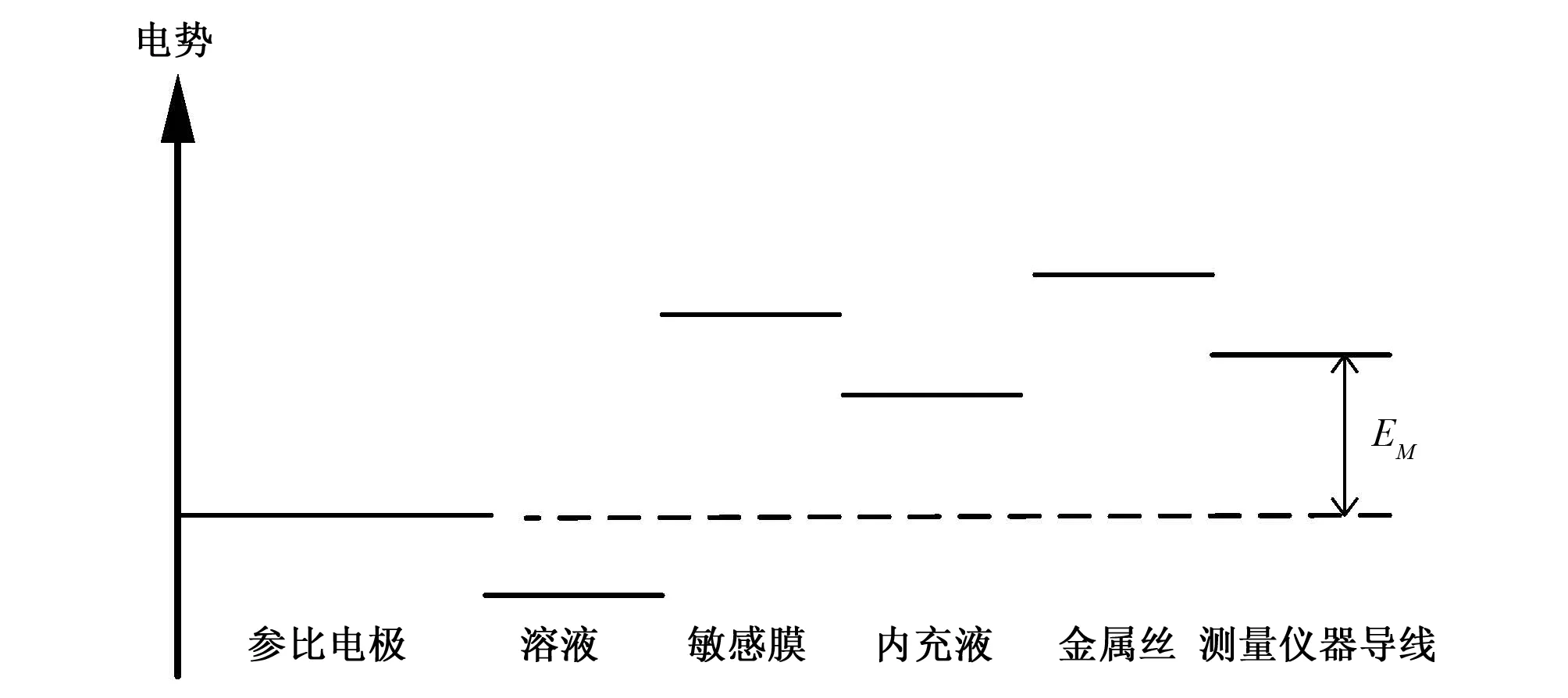
图1 离子选择电极响应电势

2 电极交叉敏感模型

离子选择电极在实际应用时，溶液中除了待测离子以外其他共存离子都会对离子选择电极敏感膜产生一定的电势响应，给最终的测量结果带来误差。对此，Nikolsky提出离子电极选择系数[10]这一概念来表征敏感膜对不同干扰离子的响应强弱情况，并由此提出了电极电势响应模型：

(2)

式中：cs1为待测溶液中的待测离子浓度；cs2为待测溶液中的共存干扰离子浓度；kij为离子电极对i离子的选择系数和对j离子的选择系数的比值(又称为离子交换平衡常数)。

Eisenman对该电极电势响应模型进行了修正并得到Eisenman-Nikolsky公式：

(3)

式中：αi为待测溶液中待测离子浓度；αj为待测溶液中共存干扰离子浓度；ni为待测离子电荷阶数；nj为共存干扰离子电荷阶数。

外界干扰对选择系数影响明显，会随着温度溶液浓度的变化而变化，需要通过实验来获得相应的数值。本文通过交叉敏感现象较大的钾离子选择电极和钙离子选择电极进行研究。

3 交叉敏感现象实验与分析

3.1 实验设备和材料

PK-1-01(BNC型)工作电极及217-01型双盐桥参比电极用来检测钾离子浓度；PCa-1-01(BNC型)工作电极及217-01型双盐桥参比电极用来检测钙离子浓度；精度0.001 g电子天平称量所需各种试剂的质量；信号检测系统用来获得电极响应电势；氯化钾试剂配置钾离子溶液；氯化钙试剂配置钙离子溶液。

3.2 实验方法

用电子天平在称量纸上称取一定质量的氯化钾试剂和氯化钙试剂，配置10-1、5×10-2、10-2、10-3、10-4mol/L一系列浓度的氯化钾溶液和氯化钙溶液，将其一一混合得到24组不同浓度的混合溶液，经检测系统测得的钾离子电极电势和钙离子电极电势如图2所示。

图2 交叉敏感离子电极响应电势

3.3 实验分析

钾离子选择电极和钙离子选择电极在24组混合溶液中进行分别测量，获得响应电势值，可以看出钾离子选择电极在同一浓度钾离子溶液中，其响应值会随着钙离子的加入而有所上升，而且加入的钙离子浓度越大，钾离子电极响应值上升越为明显，同时钙离子掺杂浓度对低浓度钾离子溶液的影响明显更大；同理钙离子选择电极对钾离子的掺杂也有相同的变化规律。

将钾离子选择电极和钙离子选择电极对两种离子的阶梯浓度比混合溶液的电势偏差百分比做成曲线图，如图3所示。

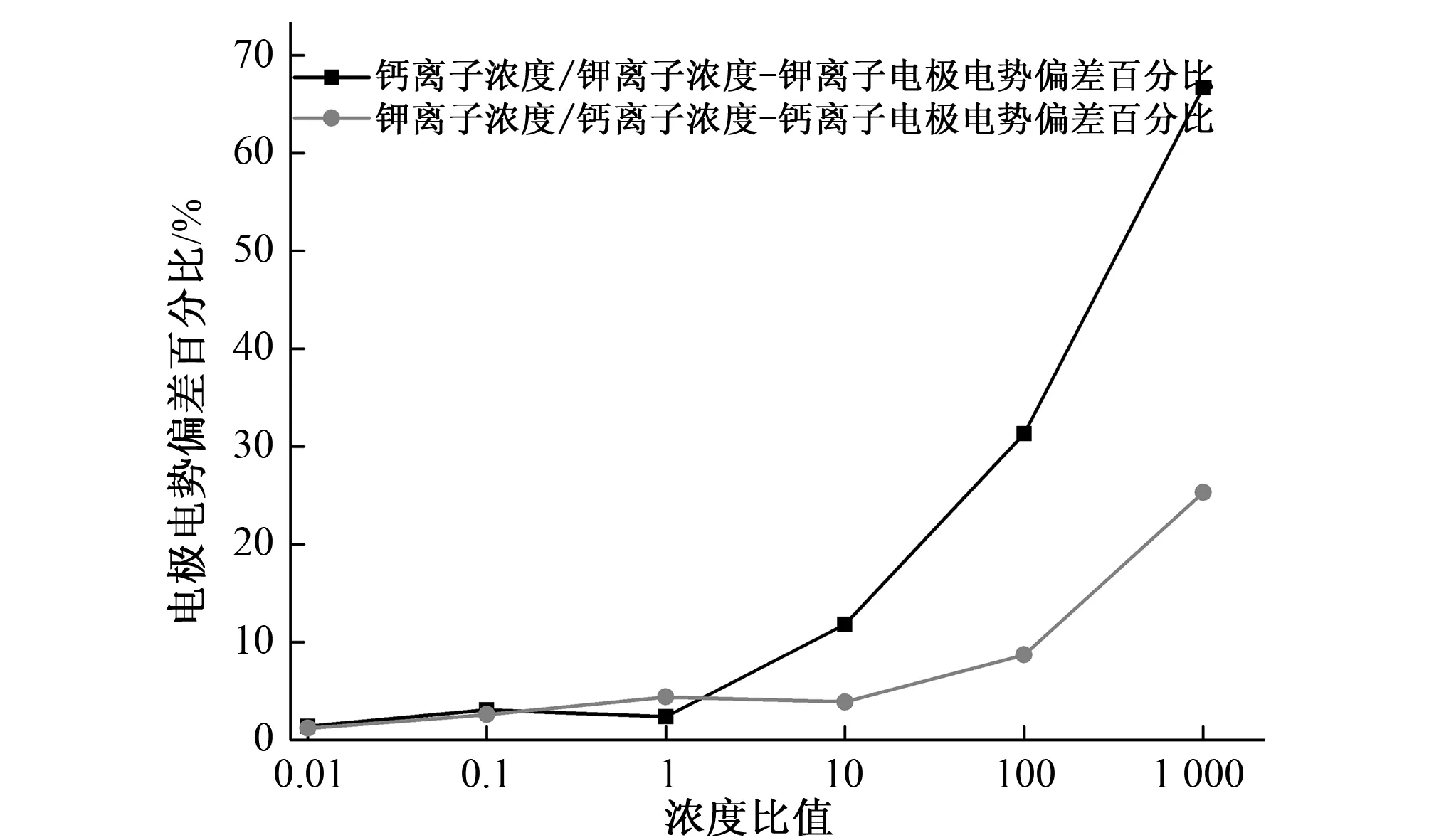
图3 电势偏差与浓度比值关联图

低浓度比值时，电极的响应偏差百分比较小，因为干扰离子相对待检测离子的浓度非常小，影响不明显，而当浓度比值逐渐增大，电极的响应偏差百分比增加幅度较大，干扰离子的影响增加，并且在相同浓度比值条件下，钾离子选择电极的偏差比值更大，即钾离子电极对钙离子的选择系数大于钙离子电极对钾离子选择系数。

4 交叉敏感抑制的SVR

4.1 SVR基础原理

SVR[11]是一种线性分类算法，基于支持向量机，建立在统计学习VC维理论和结构风险最小原理之上，根据有限的样本信息来寻求最佳的模型和学习能力。通过调节相关参数(惩罚因子c和核函数参数g)来确保全局最优解和可靠泛化性，提高预测分类的准确性。

SVR体系结构如图4所示。将n个样本变量xi(i=1,2,…,n)导入输入层中，通过与n个核函数的相互运算，作用相对应的法向量值wi(i=1,2,…,n)，引入偏量b，与各结果求和由输出层得到最终结果y。数学模型公式如下：

f(x,w,b)=sgn (+b)=

(4)

式中：sgn()为符号函数；wi为分类超平面的法向量；(xi,yi)为训练样本；αi(αi≠0)为与其对应的拉格朗日乘子；K(xi,x)为核函数。

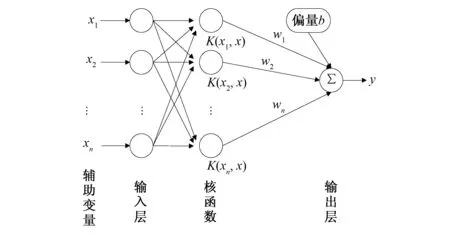
图4 支持向量机体系结构

4.2 SVR应用与分析

SVR的训练数据选择之前24组混合溶液中钾离子电极和钙离子电极电势值，通过交叉验证法获得两个电极交叉敏感模型的惩罚因子和核函数参数，其值如表1所示。

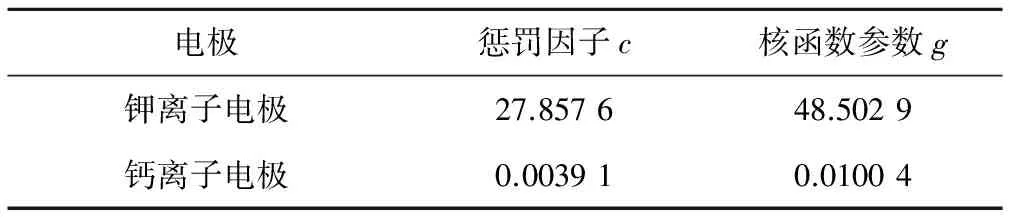
表1 两种电极的模型参数值

另配置7组浓度分别为40、80、120、160、200、240、280 mg/L的钾离子溶液和钙离子溶液，分别掺杂不同浓度的干扰离子(钾溶液中添加钙离子作为干扰，钙溶液中添加钾离子作为干扰)，将各电极对应的两个重要参数值运用到SVR训练模型来对新的数据进行决策，预测结果如图5所示。

从图5可以看出采用SVR建立的数学模型对钾离子浓度和钙离子浓度的预测具有较高的准确度，是一种有效便捷的解决离子选择电极对掺杂离子交叉敏感抑制方法，也为多种离子选择电极的混合实际应用提供了一种数学方法来消除交叉敏感干扰。

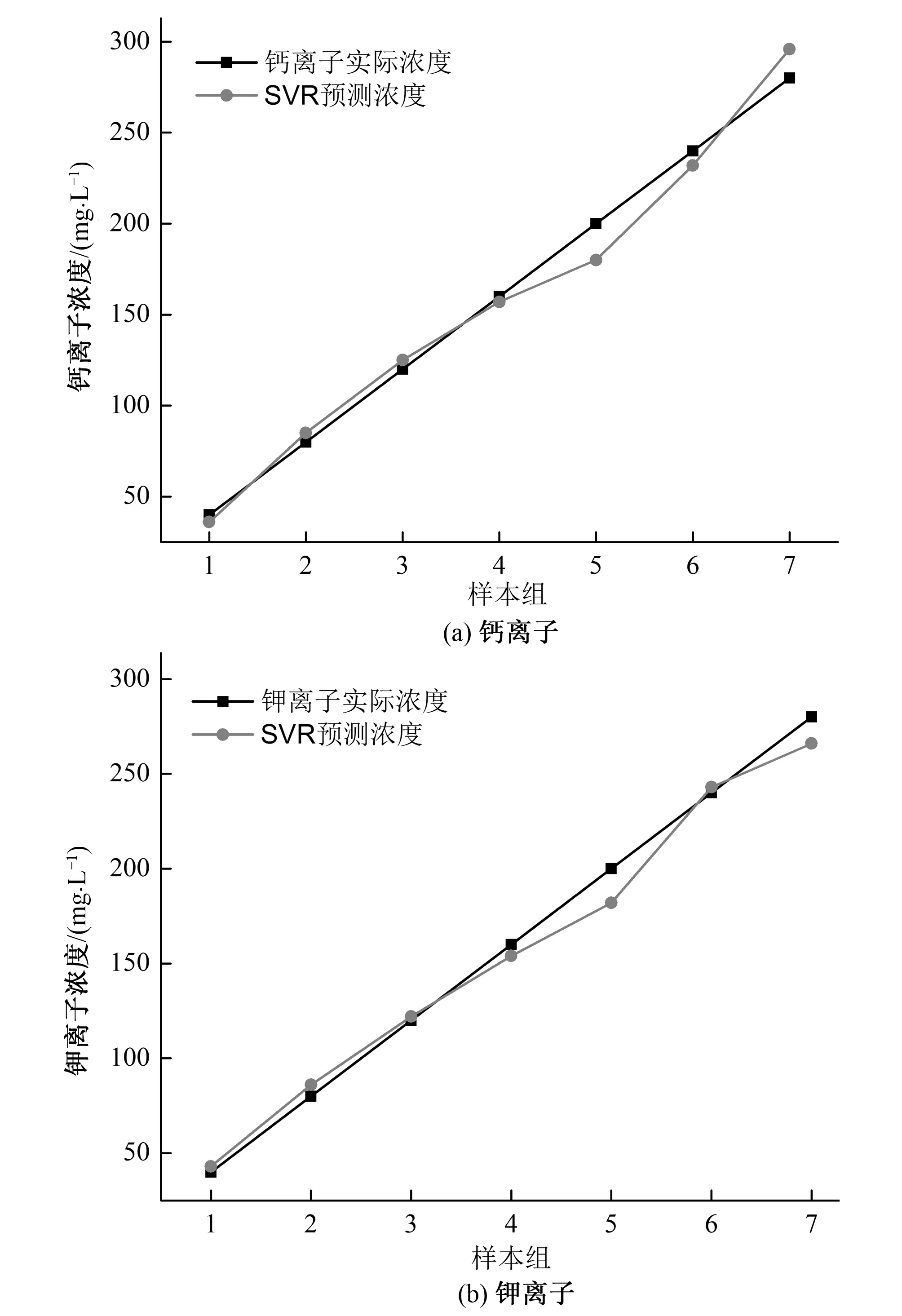
图5 SVR预测浓度与实际浓度对比

通过SVR建立的数学模型对钾离子和钙离子的14个样本组进行了离子浓度预测，与实际值的相对误差结果如表2所示。可以看出SVR数学模型对钾离子和钙离子浓度的预测值相对误差保持在±(1.00～10.00)%之间，预测值精准度较高，满足实际检测的要求。

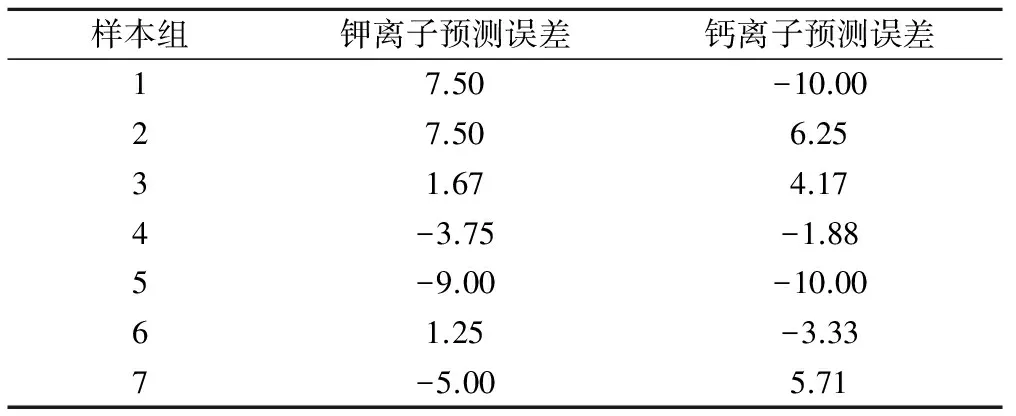
表2 SVR预测浓度相对误差 %

5 结 语

本文根据离子选择电极的结构与电势响应机理，选用最常见的钾离子选择电极和钙离子选择电极对两种离子的混合溶液进行检测实验，探索交叉敏感现象并获取相关实验数据，运用SVR算法模型对其进行分析，主要得到以下结论。

(1)离子选择电极在相同浓度的待测离子溶液中，其电势响应值会随着掺杂离子的加入而有所上升，而且加入的掺杂离子浓度越大，电极响应值上升越为明显；掺杂离子低浓度的待测离子溶液影响更大。

(2)运用SVR算法可精准预测待测离子的浓度，有效抑制了干扰离子的交叉敏感，为更多离子交叉敏感抑制提供了很好的软件解决途径。

(3)SVR预测钾离子和钙离子间的交叉敏感数值相对误差小于10%，满足水肥混合液浓度检测的实际要求。

[1] 刘云启,郭转运,刘志国，等.光纤光栅传感测量中的交叉敏感机制及其解决方案[J].光电子·激光, 1999,(2):179-182.

[2] 董玉明,张旭苹,路元刚，等.布里渊散射光纤传感器的交叉敏感问题[J].光学学报,2007,27(2):197-201.

[3] Legin A, Smirnova A, Rudnitskaya A, et al. Chemical sensor array for multicomponent analysis of biological liquids[J]. Analytica Chimica Acta, 1999,385(1-3):131-135.

[4] 周东祥,宋委远,王 鹤，等.基于BP网络的气敏传感器阵列测试分析[J].华中科技大学学报(自然科学版),2007,35(4):51-53.

[5] 简 宁,魏正英,张育斌，等.营养液多参数在线检测技术研究[J].节水灌溉, 2016,(8):190-194.

[6] 苏高利,邓芳萍.论基于MATLAB语言的BP神经网络的改进算法[J].科技通报,2003,19(2):130-135.

[7] 谢声洛.离子选择电极分析技术[M].北京:化学工业出版社,1985:1-3.

[8] 王 永,司 炜,孙德敏,等.温室营养液循环检测系统中离子选择电极的数学建模与测量[J].农业工程学报,2003,19(4):230-233.

[9] Chang C N, Cheng H B, Chao A C. Applying the Nernst equation to simulate redox potential variations for biological nitrification and denitrification processes[J]. Environmental Science & Technology, 2004,38(6):1 807.

[10] 王庆忠,宋彭生,肖应凯.电解质浓溶液的离子选择电极选择系数的测定[J].盐湖研究,2001,9(4):30-33.

[11] 苏高利,邓芳萍.关于支持向量回归机的模型选择[J].科技通报, 2006, 22(2):154-158.