不同喉管结构对文丘里施肥器性能影响的研究

谢冬辉，吴文勇，王振华，廖人宽

(1.石河子大学水利建筑工程学院，新疆 石河子 832000; 2.中国水利水电科学研究院，北京 100048)

基于农业节水灌溉发展的需求，研制高性能文丘里施肥器已成为当前国内外学者的主要研究目标。早期的研究主要集中在水力学性能测试、运行模式等实际生产应用方面[1-6]。当前对文丘里施肥器的研究主要集中在内部流道结构的数值模拟与试验研究。在试验分析方面，推演出了入口流量，吸肥量，进、出口压力之间相互作用的经验公式[7,8]，分析并获得了施肥器内部流道结构的最佳组合方式[9,10]。在数值模拟方面，建立比较多的文丘里施肥器模型并对其流道结构进行了优化设计[11-15]，但模拟数据与试验结果之间有一定误差。在施肥控制方面也有一定的研究[16-18]。然而，文丘里施肥器喉管部的流体运动状态很复杂，喉管内部结构对肥液耦合影响的研究很少见，仅集中在水肥分布、能量转化和选配方法的研究[19-22]。现阶段，对文丘里施肥器的改进主要集中在喉管进出口直径方面[23-25]，但现有的研究没有对喉管流道结构进行归纳分类，喉管进出口直径之比对吸肥性能的影响尚处在数值模拟阶段，没有得到充足的试验验证。为此，对喉管结构类型进行归纳总结，并通过试验来分析不同喉管结构对文丘里施肥器工作性能的影响，进而获取一种最佳的喉管结构，为文丘里施肥器在喉管方面的改进提供一定的参考。

1 材料与方法

1.1 试验材料

本试验选用了14种不同流道结构的文丘里施肥器，产品型号如表1所示。如图1所示，通过工业CT断层扫描测量仪(型号：TomoScope HV)得知文丘里施肥器喉管与吸肥口之间的内腔体结构有显著差异，可归纳为3种：圆柱形结构(简称C型)，锥形结构(简称T型)，椭圆形结构(简称E型)。表1中的ATP型号属于C型文丘里施肥器，有10种流道结构；GF型号属于T型文丘里施肥器，各有2种流道结构； BT 、RT型号属于E型文丘里施肥器，各有1种流道结构。

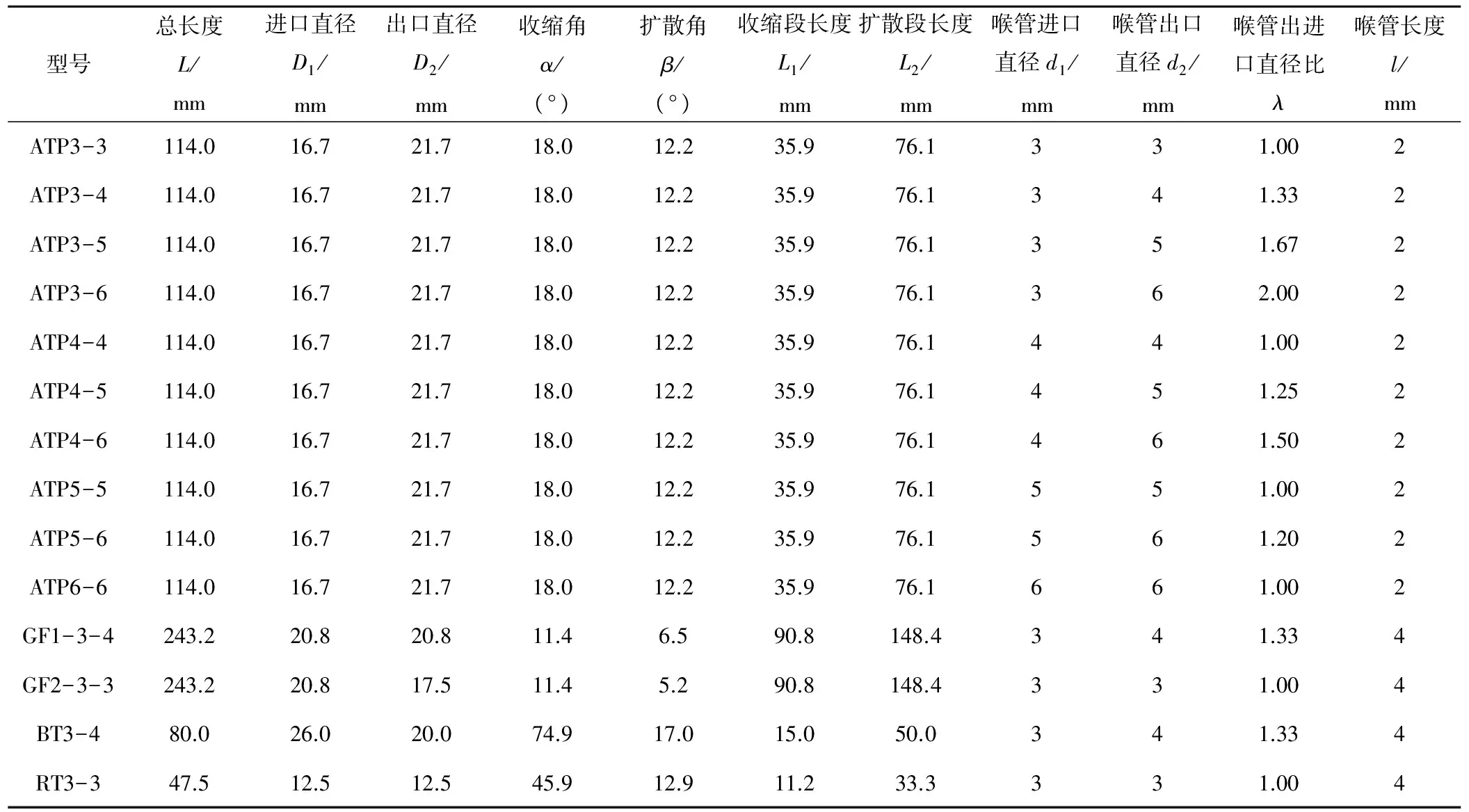
表1 文丘里施肥器基本结构参数

运用Mimics15.0软件对扫描图片进行处理，可获得试验所用文丘里施肥器内部流道的基本结构参数，见表1。其内部流道结构示意图，见图2。并引用无量纲参数λ：喉管出口直径与进口直径之比。

图2 文丘里施肥器结构示意图

1.2 试验方法

如图3所示，本次试验装置系统主要包括：变频水泵，PVC供水管路，涡轮流量计(型号为LWGY-10，量程为0.2～1.2 m3/h，精度为0.01 L/h)，电磁阀，压力传感器(型号为MPM489，量程为0～1 MPa，精度±0.5%)。其中，文丘里施肥器肥吸肥口距肥液面的高度为50 cm。对于不同尺寸的文丘里施肥器，可通过加装变径和活接头的方法来安装，而连接压力传感器的三通要根据施肥器的尺寸来更换，且压力传感器与进水口的距离应小于10 cm。图3测试软件为微灌多功能测试软件系统V1.0，软件设置的压力梯度为：0.05、0.1、0.15、0.2、0.25、0.3、0.35和0.4 MPa，每个梯度运行10 min，计算机软件会自动记录系统稳定后的各项数据：文丘里施肥器进口压力P1，文丘里施肥器出口压力P2，进口流量Q1，出口流量Q2。若测量喉管部的压力，可将吸肥管撤出并装上压力传感器，计算机系统会自动记录数据。此次试验中，出口阀门处于全开模式。

1-变频器；2-计算机系统；3-潜水泵；4-肥液桶；5-电磁阀；6-涡轮流量计Ⅰ；7-活接头Ⅰ；8-压力传感器Ⅰ；9-文丘里施肥器；10-吸肥管；11-压力传感器Ⅱ；12-活接头Ⅱ；13-涡轮流量计Ⅱ；14-出口阀门图3 文丘里施肥器试验装置示意图

由表1可知，喉管进出口直径比值λ有7种。为了增加结果分析的可信性，根据通量守恒定律，以入口流量作为主因数，通过公式(1)计算文丘里施肥器的吸肥性能。

(1)

式中：η为吸肥效率，MPa；q为吸肥量，Q2-Q1，L/h；ΔP为文丘里施肥器进出口压差，MPa。

2 试验结果与分析

2.1 喉管结构对吸肥效率和吸肥量的影响

2.1.1 喉管进出口直径对吸肥效率的影响

利用公式(1)对数据进行处理，得出施肥器入口流量Q1与吸肥效率η之间的关系，并建立回归方程见图4和表2。表2各方程均为指数函数，且底数相同，现将其指数定义为下降系数，这样便可通过下降系数的大小来宏观地反映出吸肥效率的下降速率。图4各曲线的总体变化趋势是随着入口流量的增加，吸肥效率呈递减趋势，且随着喉管进口直径的增大，吸肥效率的递减趋势变缓；喉管进口直径越小，随着流量的增加，其吸肥效率下降越迅速。

图4 C型喉管进出口直径对吸肥效率的影响

型号回归模型R2λ下降系数ATP3-3η=12．39e-0．0042Q10．9921．000．0042ATP3-4η=7．39e-0．0032Q10．9961．330．0032ATP3-5η=5．11e-0．0026Q10．9341．670．0026ATP3-6η=4．97e-0．0026Q10．9712．000．0026ATP4-4η=10．62e-0．0026Q10．9811．000．0026ATP4-5η=8．96e-0．0022Q10．9871．250．0023ATP4-6η=8．11e-0．0．0022Q10．9961．500．0023ATP5-5η=3．78e-0．0012Q10．9731．000．0012ATP5-6η=10．3e-0．0017Q10．9111．200．0017ATP6-6η=15．19e-0．0015Q10．9661．000．0015

对于喉管进口直径为3 mm的ATP型文丘里施肥器，通过试验观察，当入口流量为300 L/h时，施肥器已经开始吸肥，但吸肥量很小，此时可以认定其最佳工作区间的下限值为700 L/h；当入口流量大于700 L/h时，吸肥量不再显著明显增大，所以可以认定其最佳工作区间的上限值为700 L/h。通过设置不同的压力梯度，让入口流量分别稳定在400、500、600、700 L/h，来分析在不同入口流量下的吸肥效率与λ的关系，并建立拟合方程，见图5。由图5可以看出，在入口流量一定时，随着λ的增加，吸肥效率呈现先增加后递减的趋势。文丘里施肥器入口流量在工作中可根据实际需要而做出适当的调整，而喉管结构不能轻易改变，当λ一定时，η随着入口流量的增加而增加。图5各方程均为一元二次方程，为获得施肥器在最佳工作范围内λ的最优值，将图中的4个拟合曲线相加，此时可视为在相同的入口流量条件下η随λ增大的变化曲线，方程为：η=-2.142λ2+5.568λ+2.065。最后计算出当λ=1.27时吸肥效率最大。根据流体力学的相似性原理[26]，此结论可适用于对喉管进口直径为4、5、6 mm的ATP型文丘里施肥器的分析。

2.1.2 不同喉管结构对吸肥量的影响

若想对比不同喉管性能的优劣，需要排除收缩段和扩张段的影响，唯一的办法是保证各自的入口流量相同，而且只能将吸肥量作为评价标准(吸肥效率公式中有压差值，不能作为评价的参考)，因为喉管射流速度是影响吸肥量的直接可控因素。在入口流量相同，λ也相同的情况下，喉管射流速度也是相同的，所以此时对比吸肥量和喉管负压，可选出最优的喉管结构。以入口流量作为统一变量来分析吸肥量的变化趋势，见图6。由图6可知，当λ=1时，随着入口流量的增大，C型和T型的吸肥量增加趋势最显著，T型的最大值为180 L，C型的最大值为162 L，E型最大值为64 L，可以看出此时T型喉管的吸肥性能最优；当λ=1.33时，C型和T型的吸肥量的变化趋势有所变缓，但最大值分别稳定在250和184 L，E型的最大值最后稳定100 L。对比图6(a)和图6(b)可以看出，在工作区间内，λ的增大对吸肥量有一定的影响；在相同的入口流量下，T型喉管的吸肥量最大。综上所述，T型喉管可有效地提高吸肥量。

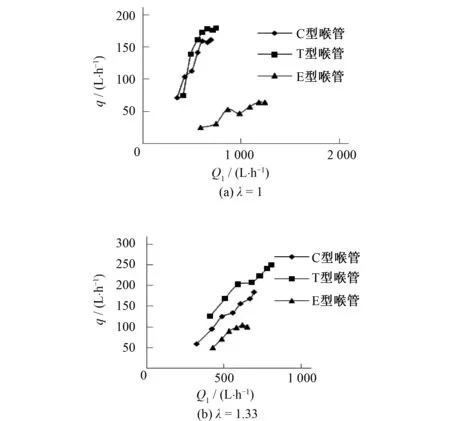
图6 不同喉管结构对吸肥量的影响

2.2 喉管对施肥器进出口压力和喉部负压的影响

2.2.1 喉管直径对进出口压差的影响

为了增加结果分析的可信性，根据通量守恒定律，以入口流量作为主因数来分析试验结果。由表1可知，ATP施肥器的各型号之间只在喉管进出口直径方面有差异性，所以在相同入口流量下，收缩段和扩张段对施肥器进出口压力差的影响力是相同的，突出了喉管对施肥器进出口压力差的单一影响。图7给出了不同喉管进口直径对施肥器进出口压力差的影响。图7(a)总体变化趋势是随着入口流量的增加，压差呈增加趋势，且随着喉管进口直径的增大，压差增加趋势变缓。无论喉管直径是多少，随着入口流量的不断增大，施肥器两端的压力差会逐步接近入口压力；喉管直径越小，压力差对入口流量的变化越敏感。图7(b)表示的是喉管进口直径为3 mm的ATP型文丘里施肥器在不同入口流量下的进出口压差与λ的关系曲线。通过计算机系统来调控入口流量的大小，以5个流量梯度来收集数据，分析后得出结论：在喉管进口直径不变时，进出口压力差与λ没有关联性；当喉管入口流量逐渐增大时，文丘里施肥器两端的压力差逐渐增大；在相同的入口流量下，随着λ的增大，文丘里施肥器的进出口压差会有很小的波动，是因为两相流(喉管水柱与肥液)相互作用而产生的不稳定现象，但其对压差的影响很小，可忽略不计。根据流体力学的相似性原理，此结论可适用于对喉管进口直径为4、5、6 mm的ATP型文丘里施肥器的分析。

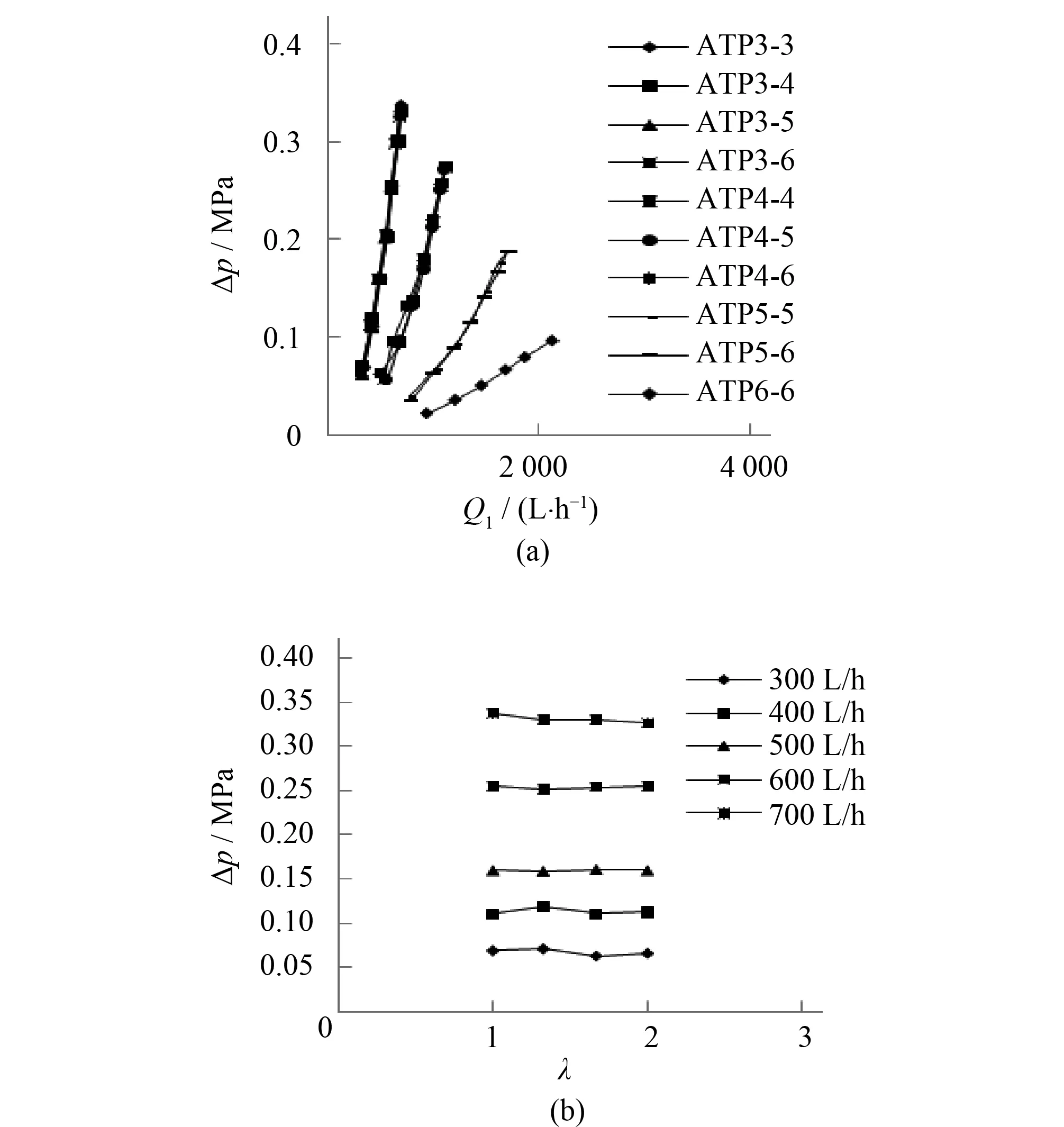
图7 喉管进出口直径对施肥器进出口压差的影响

2.2.2 不同喉管结构对喉部负压的影响

喉管负压的直接影响因素是喉管部射流速度，考虑到C、T、E型文丘里施肥器具有不同的流道结构，本次试验中这3种型号喉管的进出口直径是相同的，以入口流量作为统一变量(此时喉管部射流速度是相同的，入口流量一定时，收缩段、扩张段对喉管负压无影响)来分析不同喉管结构对喉部压力的影响，试验结果对比见图8。由图8(a)可以看出，随着入口流量的增大，喉管负压逐渐达到最大值并保持不变。C型和T型在喉管负压降到最低值的过程中，其曲线基本吻合，但T型喉管的负压值最小(-0.092 MPa)。在相同的入口流量下，E型喉管负压值的递减速率较缓慢，且最后负压值稳定在-0.08 MPa。结合图8(a)看图8(b)，可以发现，当λ由1增大为1.33时，这3种喉管部的最小负压值都有所增加，但此时T型喉管的最小负压值(-0.09 MPa)依然比C型和E型的小。本文在喉部负压值增减趋势方面的结论与文献[24]的研究结论是相同的，与之相比，本文最大的不同是比较了不同喉管结构对喉部负压的影响，且得出结论：T型喉管的吸肥能力优于C型和E型喉管。

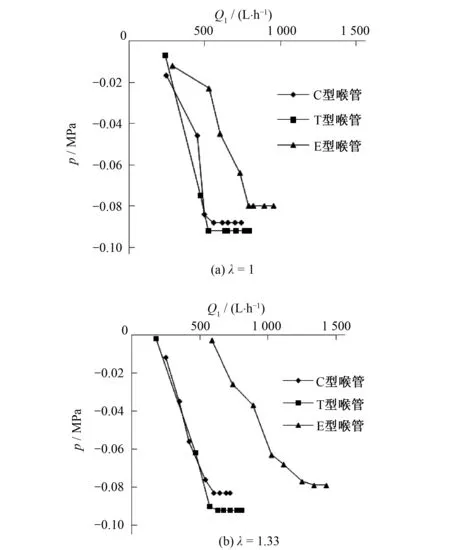
图8 不同喉管结构对喉管部压力的影响

3 结 语

通过不同喉管结构对文丘里施肥器性能影响的试验研究，得出如下结论。

(1)随着入口流量的增加，吸肥效率呈递减趋势，且随着喉管进口直径的增大，吸肥效率的递减趋势变缓；喉管进口直径越小，随着流量的增加，其吸肥效率下降越迅速。在入口流量一定时，随着λ的增加，吸肥效率呈现先增加后递减的趋势。最后计算出当λ=1.27时喉管的吸肥效率最大。

(2)在相同的入口流量下，与C型和E型相比较而言，T型喉管的吸肥效量最大。

(3)随着入口流量的增大，喉管负压逐渐达到极值并保持不变，T型喉管的负压值最小，即T型喉管提高吸肥量的能力最强。

[1] 封 俊,沈雪民,刘春和,等. 文丘里滴灌施肥器水力性能的研究[J]. 喷灌技术,1992,(1):41-43.

[2] 沙 毅,侯素娟. 并联式文丘里管施肥器试验研究[J]. 排灌机械,1995,(2):37-39,66.

[3] 金永奎,夏春华,方部玲. 文丘里施肥器系列的研制[J]. 中国农村水利水电,2006,(5):14-16,20.

[4] 李 琼,齐鄂荣. 文丘里管流动特性的实验研究[J]. 中国农村水利水电,2007,(11):65-67.

[5] Reader-Harris M J, Brunton W C, Gibson J J, et al. Discharge coefficients of Venturi tubes with standard and non-standard convergent angles[J]. Flow Measurement and Instrumentation, 2001,12(2):135-145.

[6] Doyle L G. Nozzle/venturi with pressure differentiating bypass: U.S. Patent 4,885,084[P]. 1989-12-05.

[7] 严海军,初晓一,王 敏,等. 微灌系统文丘里施肥器吸肥性能试验[J]. 排灌机械工程学报,2010,(3):251-255,264.

[8] 韩启彪,黄兴法,刘洪禄,等. 6种文丘里施肥器吸肥性能比较分析[J]. 农业机械学报,2013,(4):113-117,136.

[9] 孔令阳,范兴科. 文丘里施肥器吸肥性能试验研究[J]. 节水灌溉,2013,(7):4-6.

[10] 孙艳琦,牛文全. 文丘里管结构参数对其水力性能的影响[J]. 西北农林科技大学学报(自然科学版),2010,(2):211-218.

[11] 严海军,陈 燕,初晓一,等. 文丘里施肥器结构参数优化对吸肥性能的影响[J]. 排灌机械工程学报,2013,(2):162-166,179.

[12] 陈作炳,豆海建,陈思维,等. 文丘里管流场的数值研究[J]. 中国水泥,2005,(4):58-60.

[13] 王 淼,黄兴法,李光永. 文丘里施肥器性能数值模拟研究[J]. 农业工程学报,2006,(7):27-31.

[14] 杨 帅,刘 牮,常国峰,等. 引射式EGR系统文丘里管内流动数值模拟分析[J]. 内燃机工程,2011,(3):64-67.

[15] 邱振宇,鲍安红. 施肥器结构参数对施肥浓度影响的数值研究----基于并联式文丘里施肥器[J]. 农机化研究,2012,(4):42-45.

[16] Barnes R L. Venturi injector with self-adjusting port: U.S. Patent 6,192,911[P]. 2001-02-27.

[17] RobertoV,Montoya Y E.Operation setting nomograms for Unidrench Venturi injector[Z]. Agronomía Colombiana, 2010.

[18] 冯瑞珏,洪添胜,李加念,等. 文丘里施肥器控制性能试验分析[J]. 灌溉排水报,2011,(6):11-14,56.

[19] 韩丽娜,汪小旵. 文丘里施肥器水肥分布分析[J]. 江苏农业科学,2013,(3):385-387.

[20] 范兴科,孔令阳. 文丘里施肥器能量转化关系[J]. 排灌机械工程学报,2013,(6):528-533.

[21] 范兴科,孔令阳. 滴灌系统中文丘里施肥器的选配方法[J]. 灌溉排水学报,2014,(1):26-29.

[22] Bracy R P, Parish R L, Rosendale R M. Fertigation uniformity affected by injector type[J]. Horttechnology, 2003,13(1):103-105.

[23] 严海军,初晓一. 喉管直径对文丘里施肥器性能影响的数值模拟[J]. 排灌机械工程学报,2011,(4):359-363.

[24] 孔令阳,范兴科. 文丘里施肥器喉部负压的影响因素分析[J]. 干旱地区农业研究,2013,(6):78-82,89.

[25] Pausch J. Method of changing the length of a Venturi throat: U.S. Patent 4,026,682[P]. 1977-05-31.

[26] 欧特尔, 朱自强, 钱翼稷. 普朗特流体力学基础[J]. 北京：科学出版社，2008.