丁坝布置形式对中小河流栖息地影响的数值模拟研究

魏文杰，张小霞，张新华

(1.贵州省水利水电勘测设计研究院，贵阳 550002；2.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065)

由于河道整治工程的兴建，特别是河道渠化和硬化之后，河流已失去了天然的河流形态，适宜的水生生物栖息地环境与多样性遭到严重破坏，生态功能也大幅度衰退[1]。为改善城市河流水生态和栖息地现状，为水生生物提供必要的生存场所，国内外研究人员做了大量工作。Ch.Papadaki[2]等人采用基于一维模型的HEC-RAC模型研究了希腊山区河流生态基流对栖息地的影响。吴瑞贤等人[3]应用基于一维模型 (HEC-RAS)和河川栖地二维模型(River 2D)研究了丁坝对鱼类栖地的影响范围以及丁坝建置要素的影响。N. Poulet等人[4-7]研究了低水头坝如何改变局域栖息地特征并对鱼类群落结构及其多样性施加影响。Ali M S[8]等人为研究降低水流流速的建筑物对河道栖息地的修复作用进行了大量实验，成果表明这些建筑物能为幼鱼创造有利的生存环境。DongkyunIM[9]的研究表明巨石、丁坝和浅滩存在时的栖息地面积与没有时相比能分别提高2%、7%和131%。

这些研究成果揭示了丁坝对河道栖息地的改善作用，为进一步的研究提供了指导。同时也存在一些问题：从模型计算的角度来说，如果使用的模型精度较低，比如一维河流模型，由于对河流进行了很大的概化，在河道结构复杂或者存在水工构筑物的河道，模拟成果难以达到需要的精度；River2D虽然精度更高，但是由于没有考虑泥沙冲淤，对有丁坝作用下的河道形态变化及水流结构特征无法进行预测。此外，已有研究对具体构筑物改善栖息地的机理还揭示得不够，任需进一步深入。从丁坝的布置上来说，研究不同布置形式的丁坝对河流水生生物栖息地影响的相关研究较少。由于丁坝修建后河流的流动形态将产生明显改变，水流呈现出强紊动特性，引起丁坝周围河道的水沙结构和河床形态发生显著变化，从而也将引起水生生物栖息地及其适宜性改变。

为了探讨不同丁坝布置形式对河流栖息地的影响，本研究以水深平均二维k-ε紊流水沙耦合模型(以下简称为二维k-ε浅水模型)和IFIM鱼类栖息地模拟方法相结合，选用典型的中小河流常见鱼类(理科鱼类)作为指示物种，建立了针对中小河流典型鱼类栖息地适宜性指数和栖息地加权可用面积(以下简称为WUA)计算的水深平均二维水沙栖息地模型，进而分析6种不同的丁坝布置形式(单侧单丁坝、对口丁坝、错口丁坝、单侧双丁坝、对口双丁坝、错口双丁坝)，运用模型分析计算不同工况下水流流态和栖息地面积变化情况，探讨WUA最大的丁坝布置形式。

1 控制方程及模型建立

1.1 二维k-ε浅水模型

二维k-ε浅水模型包括水动力模块、泥沙输移和河床演变模块，具体推导及参数的选用可参考相关文献[10]。模型采用有限差分法对控制方程组进行离散，并利用蛙跳交错网格系统描述相关参数和变量[11]，以下对模型进行简要阐述。

(2)泥沙输移和河床形态模块。天然河道中的泥沙运动呈现出三维特性，但在合理假设下，一些泥沙运动特性可用二维模型描述。目前，二维泥沙数学模型有垂向和平面2种模型，本研究为平面二维模型。泥沙输移模型可进一步分成泥沙输移方程和河床演变方程。

推移质输沙率：采用Meyer-Peter与Muller提出的方法和Van Rijn提出的方法，具体方程式参考文献[13,14] 。悬移质输移过程：可用三维对流扩散方程式来描述，具体方程式见文献[10]。河床演变方程：其实质是单位时间河床变化量等于推移质和悬移质所引起的变化量之和，具体方程式见文献[10,15]。

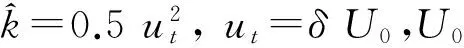
出入流边界条件：入流处为第一类边界条件，给定流量；出流处也为第一类边界条件，固定水深；泥沙输移在入流处给定泥沙浓度边界条件。

1.2 栖息地模拟

IFIM (Instream Flow Incremental Methodology)即河道内流量增加方法，是目前常用的栖息地研究方法，该方法最先应用来模拟流量和水生生物栖息地可利用性之间的定量关系，现常用于评价河道生态修复的效果。本研究采用自编的二维k-ε浅水模型程序计算河道流场、地形等参数变化，再利用微栖息地标准计算可用微栖息地适宜性及面积，最后将可用微栖息地面积加权求和得到WUA，参考针对特定物种及生命期的栖息地评价方法(HEP)[15]，WUA计算公式对于浅水模型可按下式计算：

(1)

式中：WUA为评价某物种、某些物种或某一生命期的生物栖息地加权可用面积；Ai,j为网格i,j处的单元表面面积；n、m分别为x、y方向的单元总数量；CSFij为网格i,j处的栖息地综合适宜性指数(以下简称为CSF)，其值为网格处的流速适宜性指数[以下简称为HSI(U)]、水深适宜性指数[以下简称为HSI(H)]和基质适宜性指数[以下简称为HSI(C)]3者的乘积。

1.3 指示物种及其适宜性曲线

为探讨不同丁坝布置形式对城市中小河流水生生物栖息地的影响，并且定量描述其改变值大小，选择河流生态系统中的食物链顶层的鱼类作为指示物种，本研究选择4大家鱼中常见的鲤鱼作为栖息地适宜性的指示物种。采用单变量适宜性曲线分别考虑水深、流速及基质不同时的鱼类适宜性。单变量适宜性曲线定义鱼类栖息地的适宜性值在0～1，本研究也参考了孙嘉宁[16]的鱼类适宜性曲线，给出本研究采用的流速和水深适宜性曲线，见图1。

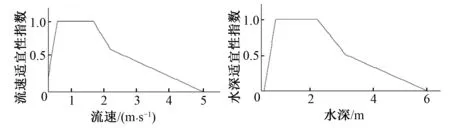
图1 流速、水深适宜性曲线

2 模型验证

2.1 模型水动力验证

采用经典的Rajaratnam与Nwachukwu丁坝绕流实验数据[17]验证水动力模块。上述实验条件及工况为：计算区域长6 m，宽0.9 m，丁坝距离入口断面2 m，见图2。计算采用结构化网格，为准确模拟丁坝周围的情况，对丁坝周围网格进行了加密处理，网格数为220×50，最小网格Δxmin=0.001 5 m，Δymin=0.001 5 m；曼宁系数采用光滑水槽底床值0.01 s/m1/3；采用冷态启动，计算时间步长取Δt=0.000 3 s，计算时间取为15 min；上游单宽流量取为0.047 8 m2/s，下游水深取为0.189 m。模拟结果中的流线图见图3，丁坝回流区长度为1.433 m，实验所测回流区长度为1.9 m。

图2 丁坝绕流计算网格划分

Rajaratnam与Nwachukwu测量了y/b=1.0、1.5、2.0、3.0、4.0(b表示丁坝的长度，y表示断面在y方向的坐标值)5个纵断面的合速度值，采用U0=0.253 m/s进行无量纲化处理以便于比较。5个断面合速度的实验值和模拟值见图4。从图4可知，合速度的模拟值和实验值较为吻合，模型很好地模拟出了丁坝坝头处流速增加的现象。在y/b=2.0断面的后半部分，模拟值和实验值有一定的出入，这可能是因为后半部分恰好处于主流区和回流区的分界部分，容易引起测量误差所致。

图3 丁坝绕流流线图

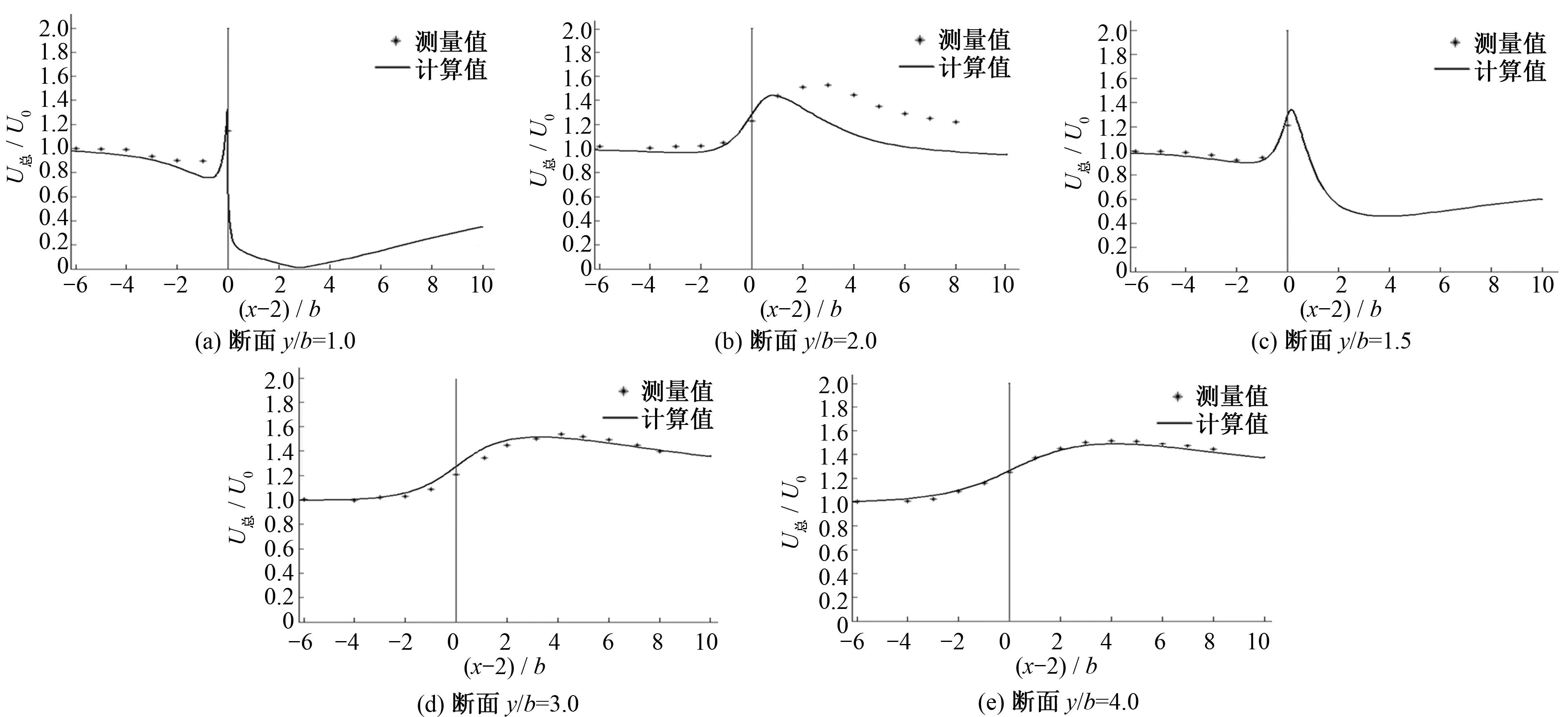
图4 典型断面合流速的计算值与实测值

2.2 模型泥沙运动验证

由于实验资料的限制，本研究通过地形变化来检验泥沙运动模型的适用性。实验采用Michiue和Hinokidani的动床试验[19]资料。Michiue和Hinokidani的动床试验数值设置为：计算区域取 7.0 m，原点定义在丁坝迎流面上游3 m处，丁坝为长0.1 m，宽0.01 m的薄直板，泥沙粒径0.6 mm，其他参数均按照原物理实验设置。采用非均匀网格划分计算区域，见图5，最小网格尺寸为0.01 m，网格数为282×27，时间步长取0.001 s。

图6中从左至右依次为Michiue和Hinokidani测量的冲刷平衡时的地形图、崔占峰[18]采用三维紊流模型模拟得到的地形图以及采用本研究的二维k-ε浅水模型计算平衡后得到的丁坝周围地形图。计算得到的最大冲深为8 cm，与原物理实验结果比较接近且稍微偏小，最大冲坑位于坝头靠上游侧，冲刷范围相比要小一些，在坝后未发生冲刷，其原因可能在于模拟试验的水流较模型试验来说紊动强度低一些。丁坝与河槽相连位置上游附近有微量淤积，坝后最大淤积厚度更小，位置往丁坝下游方向偏移更远一些，总体而言还算比较合理。

图5 泥沙模块验证 数值模拟网格划分

图6 物理实验结果、崔占峰模拟结果及浅水模型模拟结果 (单位：cm)

3 不同布置形式的丁坝对栖息地的改善作用

3.1 实验设置

作为前期机理研究的需要，为了避免天然河道中因地形、环流等干扰影响，采用顺直河槽与城市中小河流建立一定比尺关系，通过数值模拟分析顺直河槽中布置不同形式丁坝情况进行研究。岷江流经成都市华阳镇螺丝滩河段属于典型城市中小河流，且该河段原有3个丁坝群。如图7所示，河段多年平均水深约1.3 m，河段河床比降平均值约为万分之一，基质以淤泥质为主并混合有砂卵石。为有针对性的分析中小河流栖息地受丁坝布置形式的影响特性及程度，体现城市中小河流尺度，本研究暂不考虑河道断面及河道弯曲变化，简单地采用顺直水槽进行数值模拟，实验水槽与华阳丁坝河段水平长度比尺35，水深比尺26，流速比尺12.25。

图7 岷江流经成都市华阳镇螺丝滩河段原丁坝群分布

以岷江流经成都市华阳镇螺丝滩河段为背景设置模拟试验水槽，见图8，模拟试验水槽长12 m、宽2 m、高2 m，水流从水槽左端流入，流量0.012 m3/s，泥沙粒径0.8 mm。为了比较不同布置形式的丁坝对WUA的影响，先进行无丁坝清水冲刷模拟试验，河道糙率n取0.014，粗糙系数ks取0.013，计算区域采用均匀网格，网格大小为0.05 m×0.05 m，网格数为242×42，时间步长为0.001 s，模拟时长为1h(水沙运动均达到平衡稳定)。

有丁坝实验共分为6种布置形式，见图8,左半边依次为单侧单丁坝、对口单丁坝、错口单丁坝，右半边依次为单侧双丁坝、对口双丁坝、错口双丁坝，当两侧都有丁坝时，坝长为0.25 m，仅单侧有丁坝时，坝长为0.5 m，使得丁坝缩窄度保持不变，而仅改变丁坝的布置形式。

3.2 模拟结果分析

无丁坝时，水流十分平顺，流速约为0.22 m/s，可视为均匀流，水深为0.052～0.053 m，水槽中部发生极为微小的冲刷，冲刷深小于1×10-7m，在水槽边壁附近出现不连续的微小淤积，且淤积厚度小于1×10-7m。另外发现在水槽边壁进水口处有冲刷深小于1×10-5m的边壁进口冲刷，在水槽边壁出水口处有厚度小于1×10-5m的边壁出口淤积，这可能是边界条件及边壁假设造成的。由于泥沙视为均匀沙，流速分布和水深分布都较均匀，故可知微栖息地适宜性指数分布均匀。根据本研究采用的比尺，按照栖息地适宜性曲线及基质对应的栖息地适宜性指数计算得到HSI(C)为0.9、HSI(U)为0.46、HSI(H)为1，相应比尺下的河道栖息地WUA值为9 233.62。

丁坝存在时，河道水流结构发生明显变化，计算结果见图8～图12。

水深及HSI(H)值分析：由图8可知，对于单丁坝而言，单侧、对口布置时，在丁坝坝头、下游及下游一定距离处将依次出现水深增加区、第1个水深降低区和第2个水深降低区，并且对口布置时水深分布有很强的对称性，错口布置时仅有水深增加区和第1个水深降低区。由图9可知，HSI(H)值受丁坝影响较小，仅在各丁坝坝头小范围内降低，其他区域HSI(H)均为1。对于双丁坝而言，单侧布置时水深变幅略大(尤其是坝头处)；而对口、错口布置时水深变幅较小；同时，在每侧的第1个丁坝坝头处的HSI(H)值较低，其他区域HSI(H)值均为1。

流速及HSI(U)值分析：由图10和图11可知，对于单丁坝而言，单侧、对口、错口布置时，水流紊动强度依次降低，流速分布不均匀性依次降低；HSI(U)值在丁坝附近上下游一定区域内较高，远离丁坝区域和主流区的HSI(U)值较低；同时，单侧、对口、错口布置时，HSI(U)较高值区域和较低值区域的面积依次减小。对于双丁坝而言，对口和错口布置时，水流紊动强度比单侧布置小很多，且对口布置时流速对称性很强；HSI(U)值在丁坝附近上下游一定区域内较高，远离丁坝区域和主流区的HSI(U)值较低。

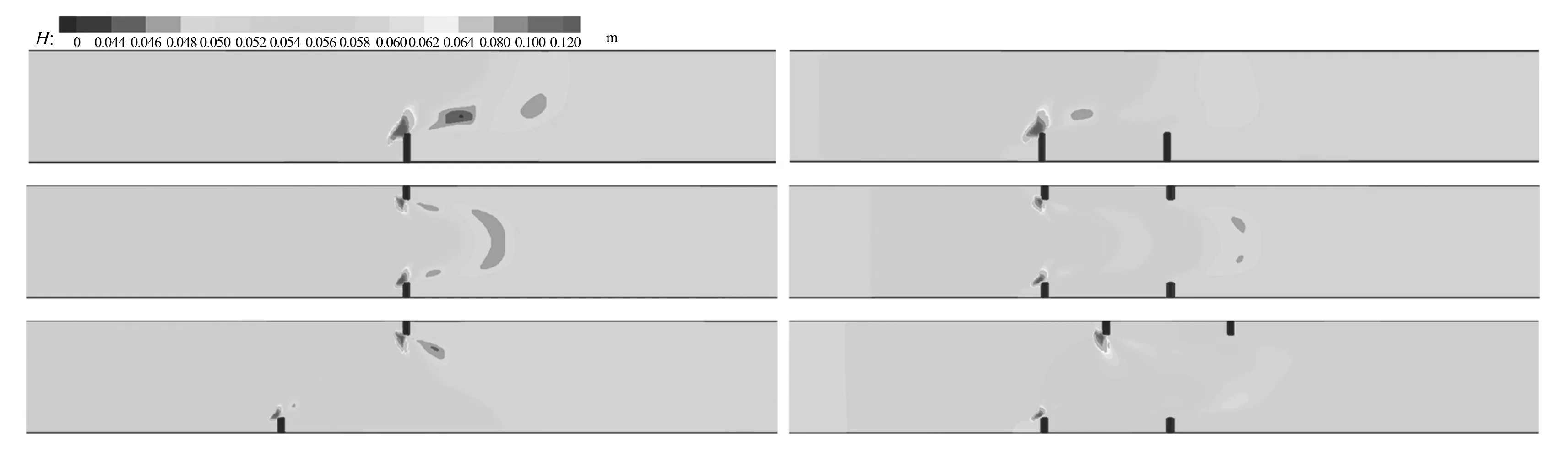
图8 不同丁坝数量及布置形式的具体水深分布

图9 不同丁坝数量及布置形式的HSI(H)值分布

图10 不同丁坝数量及布置形式的流速分布

图11 不同丁坝数量及布置形式的HSI(U)值分布

图12 不同丁坝数量及布置形式的CSF值分布

CSF值分析：由图12可知，对单丁坝而言，单侧、对口、错口布置时，CSF较高值区域和较低值区域的面积依次减小。对双丁坝而言，CSF较低值的区域面积明显大于单丁坝，而CSF较高值的区域面积在丁坝之间有所增加。

4 结 语

经模型模拟计算获得了不同丁坝布置形式的WUA值成果，见表1。对于本研究中设置的6种工况，总体来说在河流中布设丁坝对水生生物栖息地的改善效果均比较明显，WUA的增加值为26.1%～30.4%。具体情况为：河道两侧布设的丁坝数量相同时，对口布置优于错口布置，错口布置优于单侧布置。 综合来看，对口丁坝布置形式具有最优的WUA值，相比无丁坝时增加了30.4%，该种布置形式对河流栖息地有最好的改善作用。从图8和图10也可看出，对口丁坝布置时流场的对称性好，紊动强度较单侧布置小，整个流场的流态也较好。

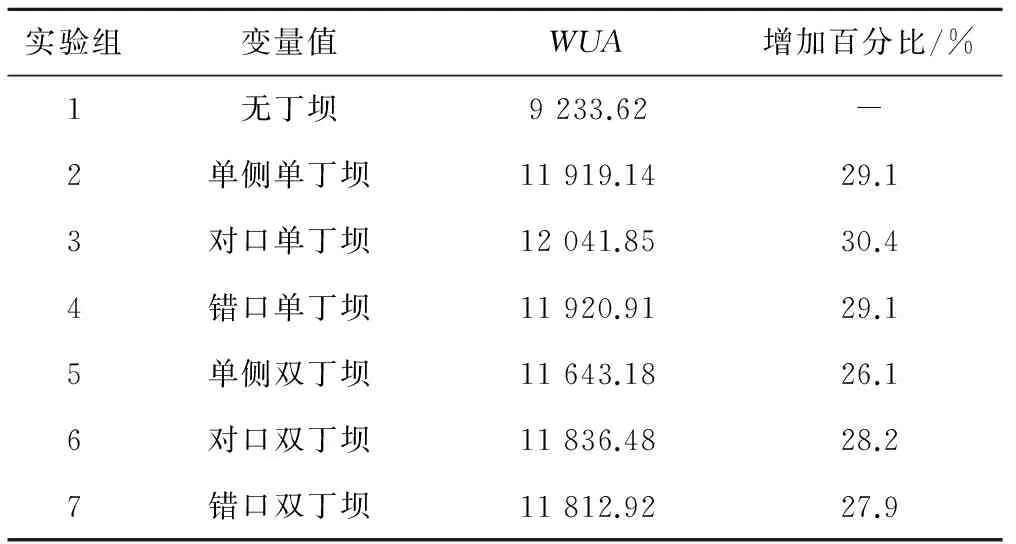
表1 不同丁坝布置形式模拟结果

□

[1] 何 冰, 高辉巧, 夏旭东. 城市河流及其生态治理规划研究[J]. 中国水土保持, 2006,(12):23-25.

[2] Papadaki C, Ntoanidis L, Zogaris S, et al. Habitat hydraulic modelling for environmental flow restoration in upland streams in Greece[C]∥ International conference protection & restoration of the environment. 2014.

[3] 吴瑞贤, 陈嬿如, 葛奕良. 丁坝对鱼类栖地的影响范围评估[J]. 应用生态学报, 2012,23(4):923-930.

[4] N Poulet. Impact of weirs on fish communities in a piedmont stream[J]. River Research & Applications, 2007,23(9):1 038-1 047.

[5] Dodd H R, Hayes D B, Baylis J R, et al. Low-head sea lamprey barrier effects on stream habitat and fish communities in the great lakes basin[J]. Journal of Great Lakes Research, 2003,29(3):386-402.

[6] Helms B S, Werneke D C, Feminella J W. The influence of low-head dams on fish assemblages in streams across Alabama[J]. Journal of the North American Benthological Society, 2011,30(4):1 095-1 106.

[7] Gillette D P, Tiemann J S, Edds D R, et al. Spatiotemporal patterns of fish assemblage structure in a river impounded by low-head dams[J]. Copeia, 2005,(3):539-549.

[8] Ali M S, Mahjabin T, Hasan M T. Dead zone creating structures in river for restoration of fish habitat[C]∥ 1st International Conference on Advances in Civil Engineering, 2012.

[9] Dongkyun I M, Kang H. Two-dimensional physical habitat modeling of effects of habitat structures on urban stream restoration[J]. Water Science & Engineering, 2011,4(4):386-395.

[10] Xiaoxia Z, Numerical simulation study of effects of spur dikes on physical habitat improvement[D]. Chengdu: Sichuan University, 2016.

[11] Quanhong L, Numerical simulation of sediment transport and morphological evolution[D]. Singapore: National University of Singapore, 2009.

[12] Rodi W. Turbulence models and their application in hydraulics —— a state of the art review[M]. IAHR, 1984.

[13] Meyerpeter E, Müller R. Formulas for bed-load transport[C]∥ Proc of Congress Iahr, 1948.

[14] Rijn L C V. Sediment transport, part I: bed load transport[J]. Journal of Hydraulic Engineering, 1984,110(10):1 431-1 456.

[15] Bovee K D. A guide to stream habitat analysis using the instream flow incremental methodology[J]. Scientific Research & Essays, 2011,6(30):6 270-6 284.

[16] 孙嘉宁. 白鹤滩水库回水支流黑水河的鱼类生境模拟研究[D]. 杭州: 浙江大学, 2013.

[17] Rajaratnam N, Nawachukwu B A. Flow near groyne-like structures[J]. J. Hydraulic Engineering, 1983,(109):463-480.

[18] 崔占峰,张小峰,冯小香. 丁坝冲刷的三维紊流模拟研究[J]. 水动力学研究与进展, 2008,23(1):33-41.