Cosserat连续体的本构参数对重力坝深层抗滑稳定的影响

涂承义，马 刚

(1. 中国电建集团 华东勘测设计研究院有限公司，杭州 311122；2. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

现阶段，重力坝深层抗滑稳定的分析方法主要是以刚体极限平衡法为主，辅以有限元法进行应力和稳定复核。由于有限元计算方法在单元网格的剖分、材料本构关系模型、单元位移模式、物理力学参数以及合理评价标准等方面存在不足，导致其在重力坝抗滑稳定计算领域的应用受到制约。另外，重力坝坝基是非连续性以及非均匀的介质，在材料变形接近或者超过峰值时，均匀的变形模式被狭窄的带状区域内的不连续位移所代替，该变形集中的带状区域即为应变局部化带。当坝基材料的应变梯度较高时，在如此小的体积范围内其应力与应变将呈现高阶次的非线性变化，经典连续介质理论所代表的统计平均值将不能如实反映坝基材料的强度和变形行为。因此，在高重力坝的抗滑稳定计算中，由于水推力以及水的软化作用，导致坝基中的相对软弱的结构面、断层等发生较大的塑性变形，形成应变局部化带；那么采用经典连续介质理论计算分析所得到结果的合理性将无法保证。

对于应变局部化问题，常规的方法是采用正则化机制[1]，包括非局部化理论、Cosserat连续体理论、梯度模型、黏性效应等。Cosserat连续体理论最早是由Cosserat兄弟于1909年提出，但直到1980年代末期才被De Borst和Muhlhaus等人应用到应变局部化的计算分析中[2-6]。Cosserat连续体理论是最基本的考虑应变梯度效应的模型[7]。

由于目前还处于发展阶段，与其他的一些局部化理论一样，Cosserat连续体理论应用于应变局部化研究还缺乏相关的材料参数取值的资料。Cosserat连续体理论的材料参数与局部剪切带的宽度有一定的关系；因此在某些情况下，可通过测量得到剪切带的宽度，以剪切带宽度与材料参数之间的关系来间接地确定Cosserat连续体理论的材料参数，这是十分重要的[8]。目前对于Cosserat连续体理论，还没有关于剪切带宽度的理论解。

运用Cosserat连续体本构模型时，为了能较好地模拟重力坝坝基深层抗滑稳定的应变局部化问题，Cosserat连续体本构材料参数选取很重要，它往往是数值模拟成败的关键，弄清这些问题也是进一步进行理论与应用研究的基础。文献[8]做了关于不同的Cosserat连续体本构材料参数对剪切带宽度及数值结果的影响的工作，指出：①在一定范围内，Cosserat剪模 的取值大小对剪切带的宽度以及计算结果几乎没有影响，在具体的数值模拟计算中，取Gc=0.5G为宜；②软化模量的取值对剪切带宽度与计算结果有很大的影响，软化模量的绝对值越大，剪切带的宽度越窄，荷载-位移曲线在达到峰值后的软化段越陡；③在一定的取值范围内，内部长度参数 越大，剪切带越宽，模拟应变软化问题中较大变形的能力越强，而对峰值极限荷载的影响不大。

本文计算分析Cosserat剪切模量Gc、软化模量hp及内部长度参数l对重力坝坝基应变局部化渐进破坏的影响。

1 基于Cosserat连续体理论的D-P弹塑性模型

Cosserat连续体理论在考虑经典连续力学中的Cauchy应力以及应变的基础上，引入了转动自由度以及与之相对应的微曲率，与微曲率能量共轭的偶应力，见图1。在平面应变问题中，每个点不仅具有平动的两个自由度，还具有转动自由度，见式(1)。

(1)

与式(1)相对应的应变及应力张量定义为：

(3)

式中：l为Cosserat连续介质材料内部特征长度；kzx、kzy为微曲率；mzx、mzy为相应的偶应力。

图1 平面应变问题中Cosserat连续体理论的应力及偶应力Fig.1 Stress and couple stress of cosserat continuum theory in plane strain case

几何方程可表示为：

ε=Lu

(5)

线弹性的本构关系表示为：

σe=Deεe

(6)

(7)

式中：λ=Ev/2 (1+v)为Lame常数；E为弹模模量；G为剪切模量；v为泊松比；Cc=αG，为Cosserat剪切模量；α为Cosserat剪切模量系数。

当α→0，1/L→0 时，Cosserat连续体便退化为经典连续体，由此可知，经典连续体可视为Cosserat连续体的一个特例。

在Cosserat连续体理论中，应力张量不变量可表示为：

I1=σ11+σ22+σ33

(8)

(9)

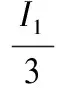
(10)

J2=a1sijsij+a2sijsji+a3mijmij/l2

(11)

J3=s11s22s33-s33(s12+s21)2/4

(12)

根据De Bost[5,6]建议，计算应力张量不变量中的系数可取为：a1=a2=1/4,a3=1/2。

此外基于Cosserat连续体理论的Drucker-Prager屈服准则可表示为：

式中：c为材料黏聚力；φ为材料内摩擦角。

假定材料的黏聚力c服从线性软化(硬化)规则，有：

(15)

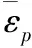
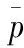
(16)

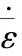
(17)

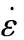
(18)

Drucker-Parager塑性势函数G用来控制材料的塑性流动方向，其应力空间中可表示为：

(20)

式中：ψ为材料的膨胀角。

2 Cosserat连续体模型中本构参数的研究

本文计算分析考虑一个坝高150 m的混凝土重力坝，重力坝坝基下存在一条2 m厚、上游出露、倾向于下游的软弱夹层。为了研究比较单元的网格密度对重力坝坝基渐进破坏过程模拟的影响，对比采用基于Cosserat连续体理论的Drucker-Prager弹塑性模型与经典的弹塑性模型的计算结果及收敛性对单元网格密度的依赖，2 m厚的软弱夹层分别采用1层、2层及3层单元划分，具体模型见图2。

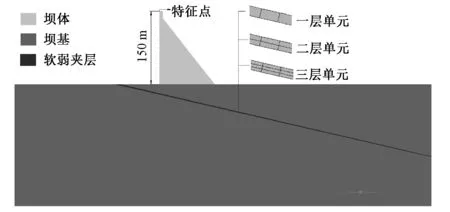
图2 重力坝坝基抗滑稳定模型Fig.2 The anti-sliding stability model of gravity dam

本文计算分析采用基于有限元的强度储备系数法对重力坝坝基的渐进破坏过程进行模拟。本文主要采用坝基等效塑性应变的分布范围进行对比分析；采用塑性屈服区贯通法、有限元迭代不收敛判据作为坝基整体失稳的2个判据，因此得到相对应的2个强度储备系数：假定对应塑性屈服区贯通的强度储备系数为Kf，对应有限元迭代不收敛的强度储备系数为Ku[10-12]。

计算中采用的材料物理力学参数见表1。基岩和软弱夹层采用基于Cosserat连续体理论的Drucker-Prager弹塑性模型，坝体混凝土采用线弹性模型。为了能准确地比较软弱夹层不同单元网格密度对坝基渐进破坏过程模拟的影响，本文分析计算中不考虑基岩的软化，只考虑软弱夹层的软化；因此基岩的软化模量hp取为0，Cosserat剪模系数取α为0.001，即Gc=0.001G，内部特征长度l取为0.000 1 m。软弱夹层的Cosserat剪模系数α、软化模量hp、内部特征长度l则根据不同的计算条件选取不同的值。

表1 各材料的物理力学参数Tab.1 Physico-mechanical parameters of materials

文献[9]列出了基于Cosserat连续体理论Drucker- Prager弹塑性模型在ABAQUS中实现的UEL自定义单元接口二次开发；采用强度储备系数法，模拟重力坝坝基应变局部化渐进破坏过程，并对比Cosserat连续体理论与经典连续体理论的结果。本文主要分析Cosserat剪切模量Gc、软化模量hp及内部长度参数l对重力坝坝基渐进破坏的影响。

2.1 Cosserat剪切模量Gc对计算结果的影响

选取软弱夹层为一层单元的模型计算分析，比较软弱夹层的不同剪切模量Gc对结果的影响。软弱夹层的软化模量hp=-10 MPa，内部长度参数l=0.01 m，弹性模量E=1 GPa，剪切模量G=0.37 GPa；Cosserat剪切模量Gc分别取为0.05G、0.10G、0.25G、0.50G、1.0G、2.5G、10.0G、50.0G。

对于不同的Cosserat剪切模量Gc，计算得到的塑性屈服区贯通的强度储备系数Kf及有限元迭代不收敛的强度储备系数Ku如表2所示，相应的Kf与Ku所对应的塑性屈服区分布见图3～图5。

表2 不同的Cosserat剪切模量对应的Kf与KuTab.2 Kf and Ku of different Cosserat shear modulus

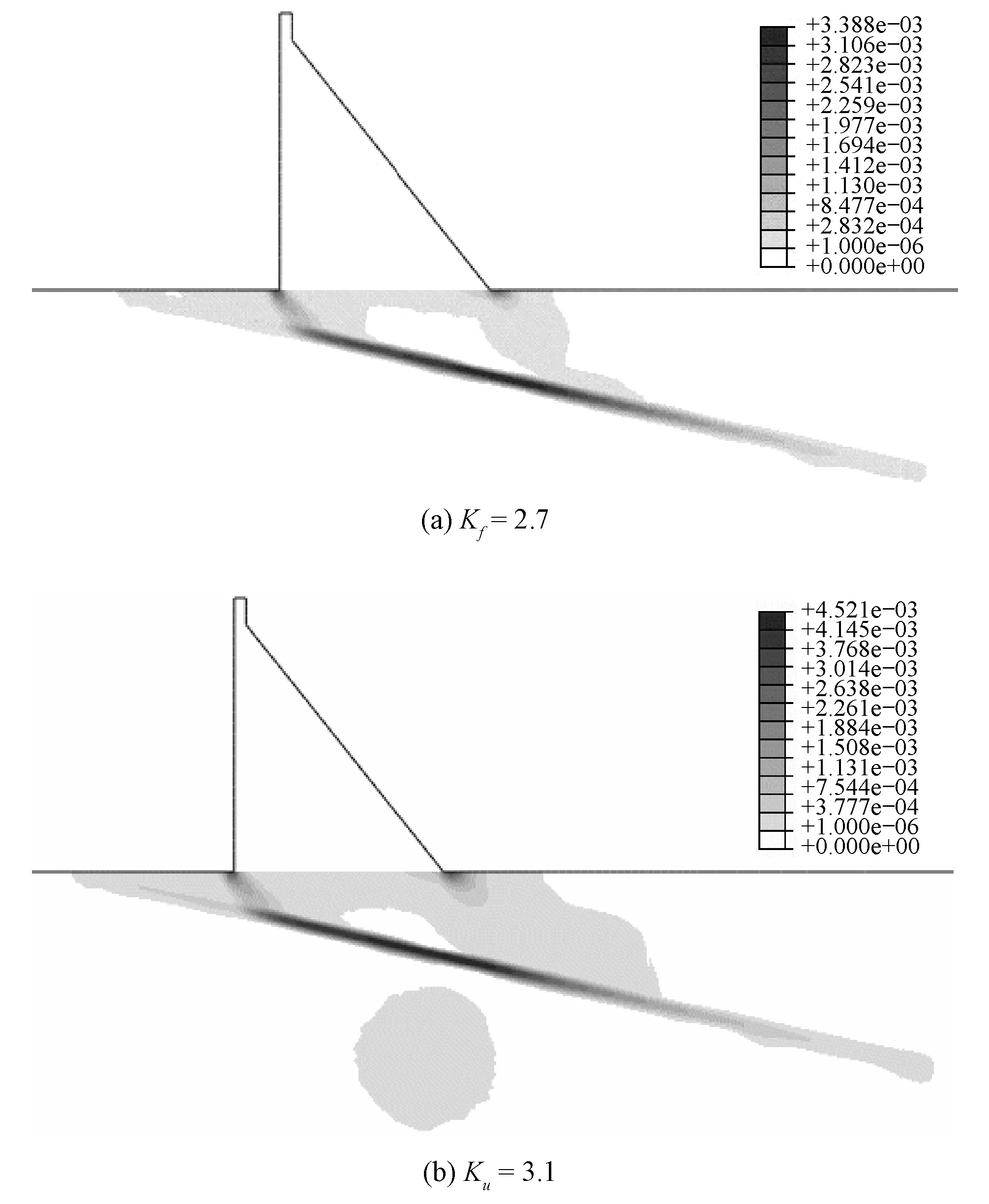
图3 Cosserat剪切模量为0.05 G时塑性屈服区分布Fig.3 Plastic yield zone when Cosserat shear modulus is 0.05 G

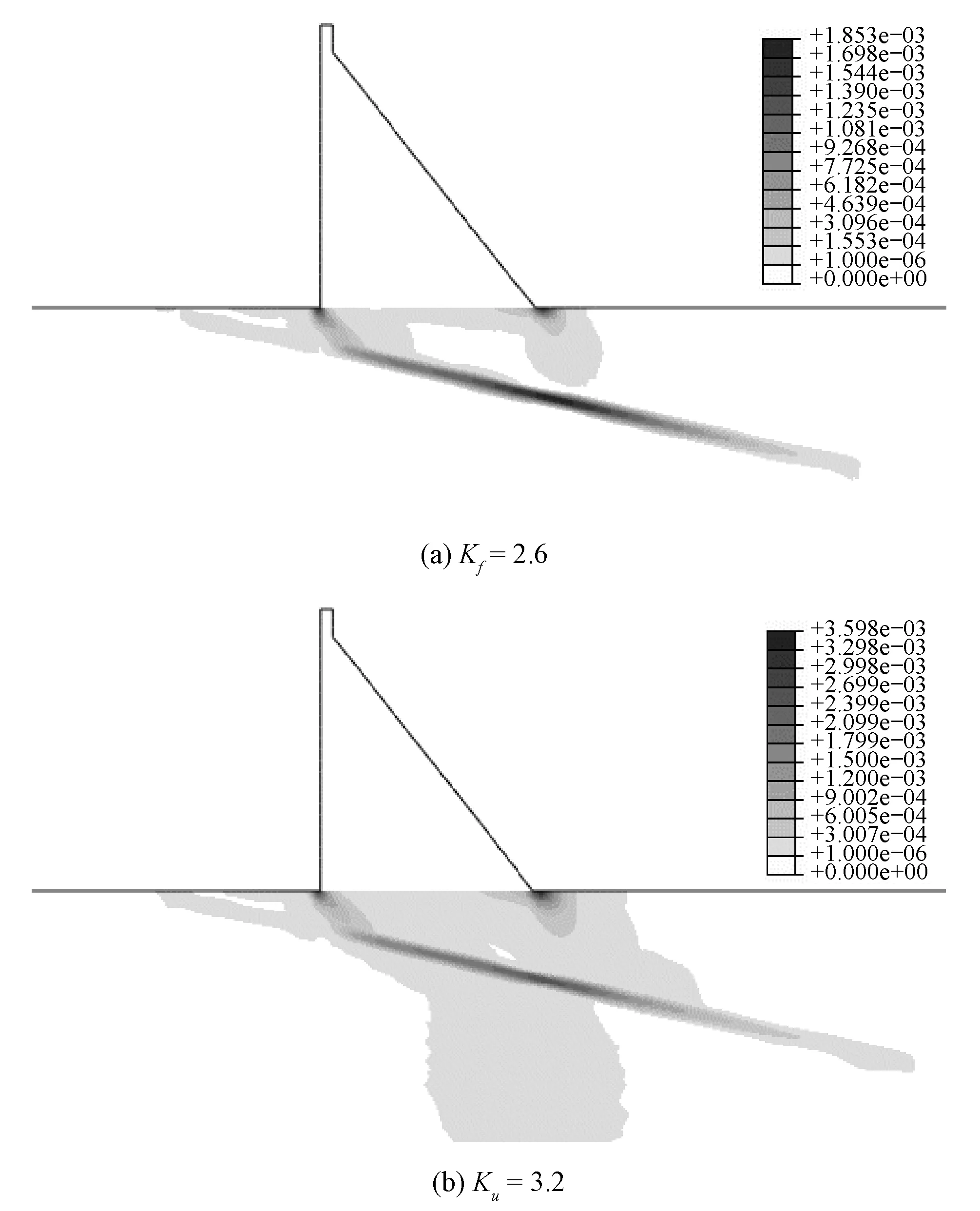
图4 Cosserat剪切模量为0.5 G时塑性屈服区分布Fig.4 Plastic yield zone when Cosserat shear modulus is 0.5 G

图5 Cosserat剪切模量为50 G时塑性屈服区分布Fig.5 Plastic yield zone when Cosserat shear modulus is 50 G

由表2及图3～图5可知，当Cosserat剪切模量Gc为0.05G时，Cosserat连续体接近退化为经典连续体，此时Kf为2.7；较 取其他值时的Kf=2.6时大0.1。Cosserat剪切模量Gc小于0.5G时，Ku=3.1；Cosserat剪切模量Gc大于0.5G时，Ku=3.2。对于同一强度储备系数，不同的Cosserat剪切模量 所对应的塑性屈服区的分布基本相同。因此，在一定的取值范围内，Cosserat剪切模量Gc对Kf与Ku及渐进破坏过程影响不大。De Borst，Steinmann，李锡夔等在将Cosserat连续体理论应用于应变局部化的研究中，基本按Gc=0.5G，本文亦推荐Gc取0.5G。

2.2 软化模量hp对计算结果的影响

选取软弱夹层为一层单元的模型计算分析，比较软弱夹层不同的软化模量hp对计算结果的影响。软弱夹层的剪切模量Gc=0.50G，内部长度参数l=0.01 m；令h0=-10 MPa，软化模量hp分别取为0.01h0、0.1h0、0.2h0、0.5h0、1.0h0、2.0h0、5.0h0、10.0h0、100.0h0，即-0.1、-1.0、-2.0、-5.0、-10.0、-20.0、-50.0、-100.0、-1 000.0 MPa。

对于不同的软化模量hp，计算得到的塑性屈服区贯通的强度储备系数Kf及有限元迭代不收敛的强度储备系数Ku如表3所示，相应的Kf与Ku所对应的塑性屈服区分布见图6～图8。

由表3及图6～图8可知，当软化模量取值 在-0.1与-10.0 MPa之间时，各软化模量对应的塑性屈服区贯通对应的Kf及有限元迭代不收敛对应的Ku均相同：Kf=2.6，Ku=3.2。当hp达到-50.0 MPa时，强度储备系数为2.0时，计算由于迭代不收敛而退出，坝基塑性屈服区未贯通，即Ku=2.0，Kf不存在；当hp=-100.0 MPa时，Ku=1.3。当hp=-1 000.0 MPa时，当强度储备系数降低时，坝基中完好基岩出现较大的塑性屈服区，而软弱夹层却没有屈服，与实际认知不相符，计算结果失去意义。

因此，软化模量的取值对坝基应变局部化的渐进破坏模拟有较大的影响。软化模量的取值在一定的范围内，Kf及Ku相同，渐进破坏过程基本相同；当软化模量的绝对值超过一定值时，计算在坝基未贯通时即迭代不收敛；当软化模量的绝对值进一步增大时，降低坝基抗剪断强度过程中软弱夹层未屈服，与实际不符。

表3 不同的软化模量对应的Kf与KuTab.3 Kf and Ku of different softening moduluses

图6 软化模量为-10.0 MPa时塑性屈服区分布Fig.6 Plastic yield zone when softening modulu is -10.0 MPa

图7 软化模量为-50.0 MPa时塑性屈服区分布Fig.7 Plastic yield zone when softening modulu is -50.0 MPa

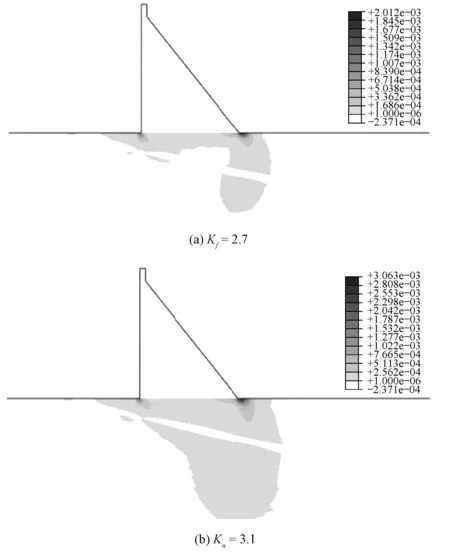
图8 软化模量为-1 000.0 MPa时塑性屈服区分布Fig.8 Plastic yield zone when softening modulu is -1 000.0 MPa

2.3 内部长度参数l对计算结果的影响

选取软弱夹层为一层单元的模型计算分析，比较软弱夹层不同的内部长度参数l对计算结果的影响。软弱夹层的剪切模量Gc=0.50 G，软化模量hp=-10MPa；软弱夹层的厚度B=2m，内部长度参数 分别取为0.001 B、0.005 B、0.01 B、0.02 B、0.03 B、0.04 B、0.05 B、0.10 B、0.20 B、0.50 B，即0.002、0.01、0.02、0.04、0.06、0.08、0.10、0.20、0.40、1.00m。

对于不同的内部长度参数l，计算得到的塑性屈服区贯通的强度储备系数Kf及有限元迭代不收敛的强度储备系数Ku如表4所示，相应的Kf与Ku所对应的塑性屈服区分布见图9～图11。

文献[4-8]在将Cosserat连续体理论应用于应变局部化的研究中，内部长度参数基本取在0.01 B～0.1 B范围内，均能产生一定的正则化效果，并对剪切带宽度影响大。而本文计算所得到的软弱夹层内部长度参数的取值对Kf、Ku及渐进破坏过程塑性屈服区的发展基本没影响，原因在于软弱夹层虽然由于最先屈服，在计算迭代收敛中起决定作用，但在整个系统中所占的比例较小，对于基岩的屈服破坏范围的影响较小，因此内部长度参数的取值不同，对渐进破坏过程塑性屈服区的发展影响不大。

表4 不同的内部长度参数对应的Kf与KuTab.4 Kf and Ku of different internal lengthes

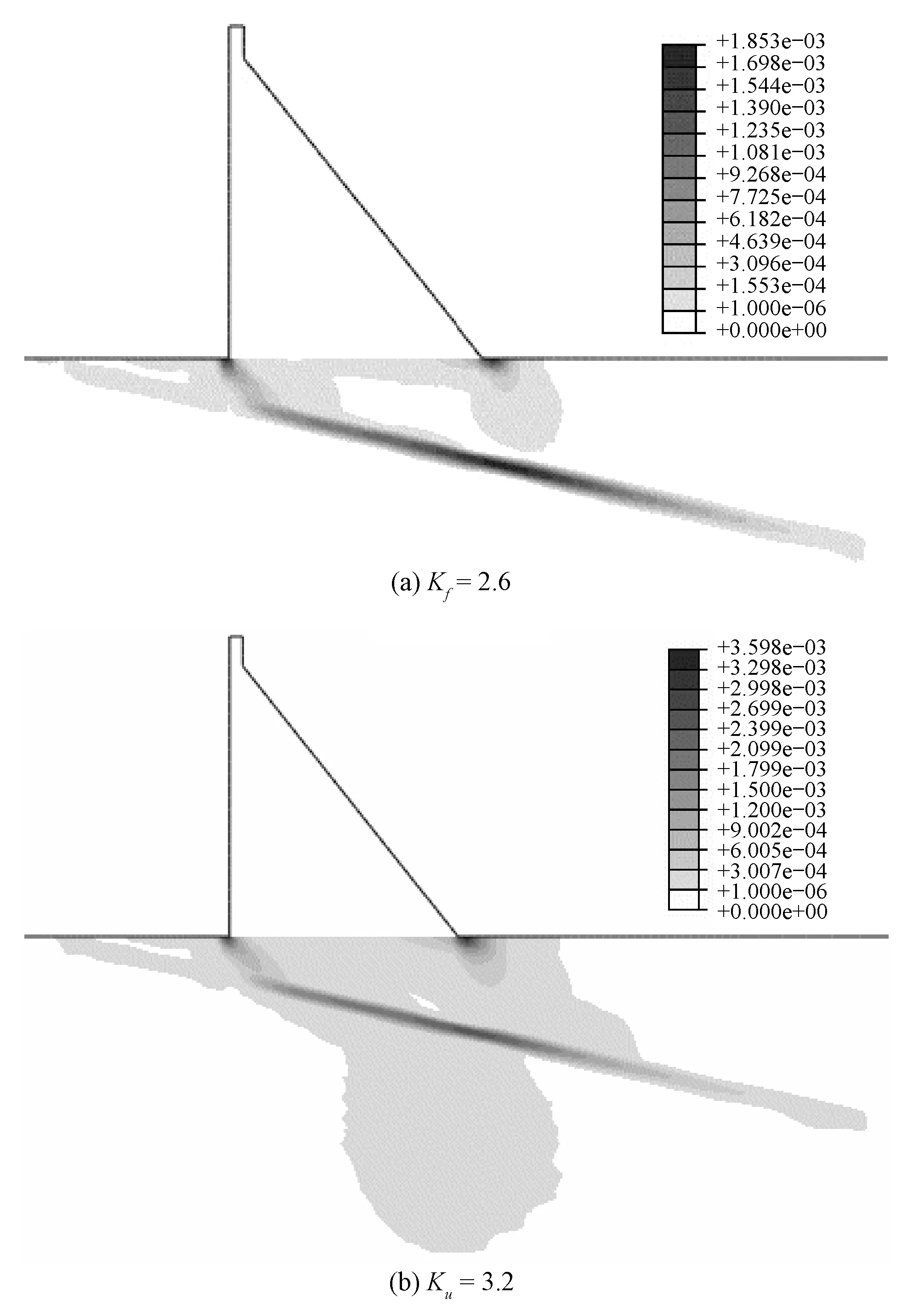
图9 内部长度参数为0.001 B时塑性屈服区分布Fig.9 Plastic yield zone when internal length is 0.001 B

3 结 语

(1)在一定的取值范围内，Cosserat剪切模量Gc对Kf、Ku及渐进破坏过程影响不大。

(2)软化模量hp的取值对坝基应变局部化的渐进破坏模拟有较大的影响。hp的取值在一定范围内，Kf、Ku及渐进破坏过程基本相同；当hp的绝对值超过某一定值时，降低坝基抗剪断强度过程中软弱夹层未屈服，与实际不符。

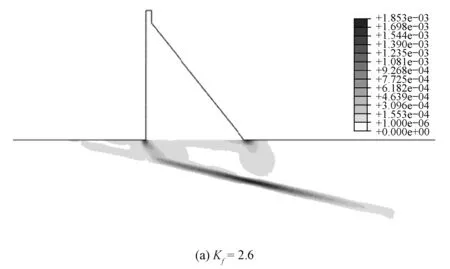
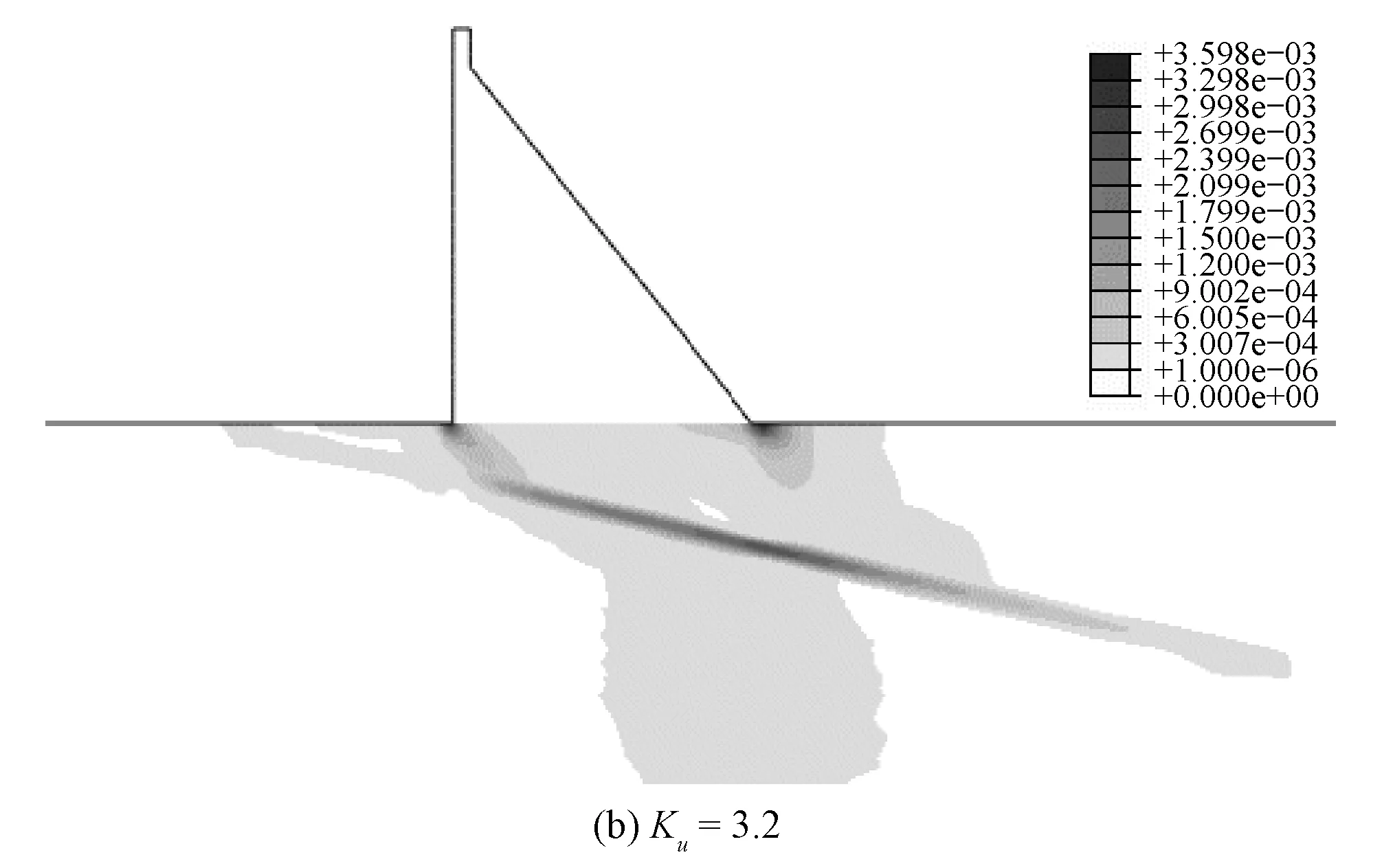
图10 内部长度参数为0.05 B时塑性屈服区分布Fig.10 Plastic yield zone when internal length is 0.05 B

图11 内部长度参数为0.50 B时塑性屈服区分布Fig.11 Plastic yield zone when internal length is 0.50 B

(3)软弱夹层的内部长度参数l的取值对Kf、Ku及渐进破坏过程塑性屈服区的发展影响不大。

□

[1] 王小平，徐卫亚．应变局部化问题中的正则化机制探讨[J]．岩土力学，2008，29(11)：2 997-3 002．

[2] Muhlhaus H B. Application of Cosserat theory in numerical solutions of limit load problems [J]. Ing. Arch., 1989,59(2):124-137.

[3] Muhlhaus H B, Vardoulakis I. The thickness of shear bands in granular materials [J]. Geotechnique, 1987,37(3):271-283.

[4] de Borst R, Sluys L J. Localization in a Cosserat continuum under static and dynamic loading conditions [J]. Comput. Methods Appl. Mech. Eng., 1991,90(2):805-827.

[5] de Borst R. A generalization of J2-flow theory for polar continua[J]. Comput. Methods Appl. Mech. Eng., 1993,103(3):347-362.

[6] de Borst R. Simulation of strain localization：a reappraisal of the Cosserat continuum[J]. Eng. Comput., 1991,8(4):317-332.

[7] 李锡夔，唐洪祥．压力相关弹塑性Cosserat连续体模型与应变局部化有限元模拟[J]．岩石力学与工程报，2005，24(9)：1 497-1 505．

[8] 唐洪祥．基于Cosserat连续体模型的应变局部化有限元模拟[D]．辽宁大连：大连理工大学，2007.

[9] 马 刚，涂承义，常晓林，等．基于 Cosserat 连续体理论的重力坝深层抗滑稳定分析[J]．四川大学学报(工程科学版)，2012，44(5)：57-63．

[10] 蒋春艳，常晓林，周 伟．用于重力坝抗滑稳定分析的分项系数有限元方法[J]．水力发电学报，2006，25(2)：16-20．

[11] 周 伟，常晓林，徐建强．基于分项系数的重力坝深层抗滑稳定分析[J]．岩土力学，2007，28(2)：315-320．

[12] 常晓林，陆述远．重力坝均质坝基的失稳机理研究[J]．武汉水利电力学院学报，1989，6(1)：1-6．