不同目标函数对水文模型模拟效果影响研究

张如强，高红凯，刘俊国,，田 勇

(1.北京林业大学自然保护区学院，北京 100083; 2.亚利桑那州立大学，亚利桑那州坦佩 AZ85282； 3.南方科技大学环境科学与工程学院，广东 深圳 518055)

水文模型作为模拟水文过程和认识水文规律的有效工具，已广泛应用于科学研究领域和解决实际问题，如洪水分析与预报、水资源管理等[1,2]。水文模型是对现实世界的简化和抽象，模型中包含难以直接测量的参数，所以需要对模型参数进行率定，间接得到这些参数值[3,4]。另外，无论选用哪种水文模型，都需要对模型的模拟效果进行评价[5]。模型的率定和模拟效果的评价通常是对比模拟流量和观测流量，使目标函数值最大或最小[6,7]。

模型的模拟效果与目标函数的选取直接相关[8]。纳什系数(E)是模型率定过程中应用最为广泛的目标函数，也是评价模拟效果的重要数值指标[7,9,10]。但是，纳什系数存在不足之处：计算公式中观测流量与模拟流量之差采用平方的形式，这导致洪峰的影响较基流大，即纳什系数对洪峰过于敏感[7]。因此产生了纳什系数的变形形式，主要包括以自然数为底的对数形式(Eln)、开方形式(Esqrt)、绝对值形式(Eabs)和相对值形式(Erel)[6,7,11,12]。尽管这些变形形式已经被学者应用于模型率定和评价[5,6,13]，但这些目标函数的选取对模拟效果影响的研究相对较少，选择哪种变形形式更为合理这一问题尚未得到圆满解答。

本研究拟通过将纳什系数、各个变形形式设定为目标函数，以纳什系数、相关系数、平均绝对误差和平均值之差4个数值指标综合分析模型模拟效果，探索不同目标函数的选取对模拟效果的影响。

1 研究区域概况及数据来源

黑河发源于祁连山，流经甘肃、青海、内蒙古自治区，最后流入居延海，干流全长821 km，是我国西北地区第二大内陆河。以莺落峡和正义峡为界，黑河流域分为上、中、下游。本文的研究区为黑河上游，位于祁连山西北，面积约1.000 9 万km2，海拔高度介于1 700～4 900 m；研究区覆被包括森林(20%)、草地(52%)、裸地(19%)、湿地或洪泛区(8%)和永久性冰川雪地(0.8%)。研究区降雨集中，超过80%大降雨分布在5-9月；多年平均降雨和潜在蒸散发为430和520 mm/a。

数据来源于寒区旱区科学数据中心。研究使用数据为日降雨、日平均气温和逐日的径流量。其中，气象数据为托勒站、祁连站、野牛沟站、张掖站四个气象站1959-1979年和1990-2006年日降雨和日平均温度，径流数据为莺落峡水文站相应时间观测流量。研究区位置、覆被以及气象站水文站位置见图1。

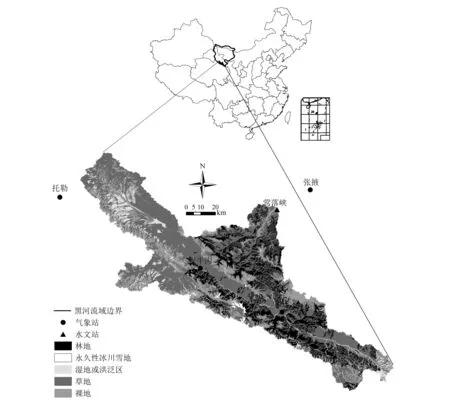
图1 研究区位置、黑河上游覆被及气象、水文站点分布Fig.1 Location and Land cover of Upper Heihe River basin and distribution of the meteorological andhydrologic stations in and around upper Heihe

2 研究方法

2.1 模型简介

地形与地质条件、土壤类型、气候、地表覆被等密切相关，而这些正是影响水文过程的主要因素。地形综合反映了流域下垫面信息，在不同尺度上影响了降雨-径流过程[14]。基于这一假设Gao等[15]开发了半分布式水文模型FLEX-Topo，并应用于黑河上游，取得了满意的模拟效果[15]。因此，本文研究中采用FLEX-Topo模型[15]。依据地形因素将流域分为4种水文景观类型。不同水文景观类型的产汇流特点不同，因此，模型中采用了不同的产汇流机制，使模型具有了半分布式的特点。依据降雨形成径流的过程，模型包含了5个水箱：积雪水箱(Sw)、植被冠层截留水箱(Si)、非饱和土壤层水箱(Su)、快速退水水箱(Sf)和慢速退水水箱(Ss)。整个模型通过5个水箱模拟降雨经过截留(I)、蒸散发(Ei&Ea)、优先流(RfB)、壤中流(Qf)、地下径流(Qs)等最终流入河网的过程。模型结构见图2。FLEX-Topo模型包含24个参数，参数含义及取值范围见表1。

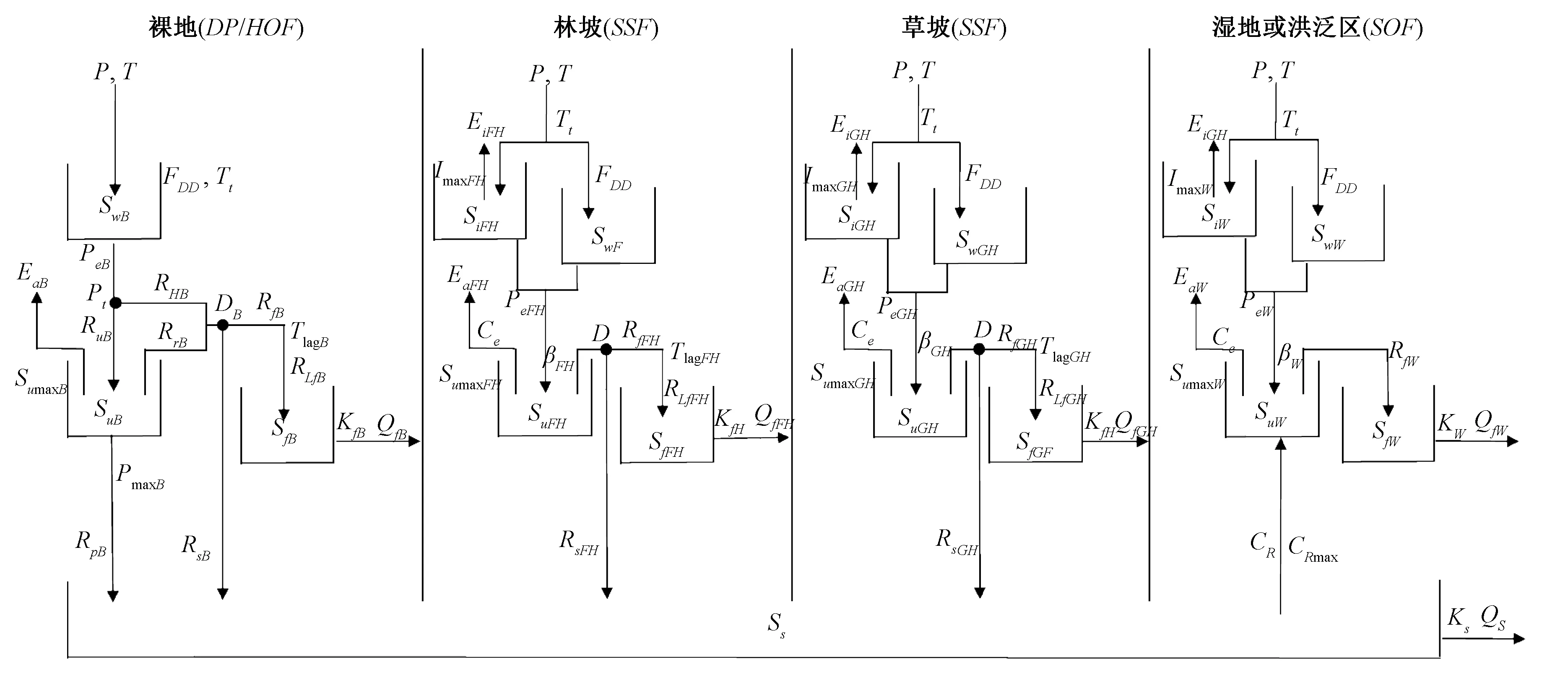
图2 FLEX-Topo 模型结构[15]Fig.2 The structure of the FLEX-Topo model

参数名称取值范围含义FDD[1，8] 度日模型参数，表征当温度高于Tt时，每升高1°每日融化形成的水量Tt[-2．5，2，5] 当温度高于该参数时，产生截留Pt[5，35] 当有效降雨大于该参数时，发生霍顿超渗产流SumaxB[5，500] 裸地景观土壤最大持水能力PmaxB[0．1，10] 裸地景观的最大深层渗漏能力DB[0，1] 裸地景观中将径流分成流入快速退水水箱和慢速退水水箱的参数TlagB[0，5] 裸地景观中径流进入快速退水水箱的滞后时间KfB[2，50] 裸地景观中存储于快速退水水箱中水流入河网的时间ImaxFH[1，10] 林坡景观最大截留量SumaxFH[100，1000] 林坡景观土壤最大持水量βFH[0．1，5] 表征景观的空间异质性，用于计算林坡的径流系数D[0，1] 林坡和草坡景观中将径流分成流入快速退水水箱和慢速退水水箱的参数TlagFH[0，5] 林坡景观径流进入快速退水水箱的滞后时间KfH[1，20] 林坡和草坡景观中快速退水水箱中的水流入河网的时间

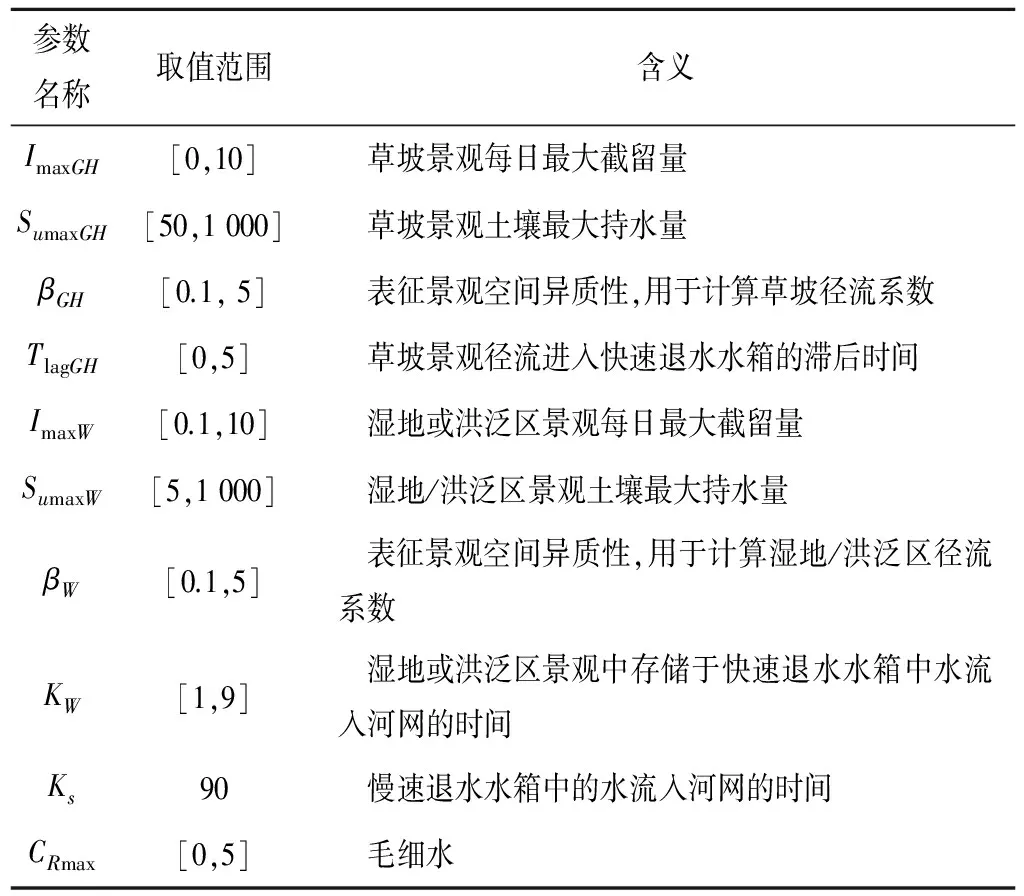
续表1 FLEX-Topo模型参数及参数取值范围

模型的输入数据为DEM、日降雨、日平均温度，输出为逐日的蒸散发(Ei&Ea)、径流量(Qf&Qs)、渗流量(RfB&f)。DEM主要用于生成HAND(Height Above the Nearest Drainage)[15-18]和坡度。黑河上游依据这两个因素分为4种水文景观类型，即裸地(bare soil/rock)、林坡(forest hillslope)、草坡(grass hillslope)、湿地或洪泛区(wetland/flood plain)，其中，裸地的产流机制主要为深层渗漏补给地下水(DP)和超渗产流(HOF)；林坡和草坡的产流机制为壤中快速径流(SSF)，主要是优先流；湿地或洪泛区的产流机制为蓄满坡面产流(SOF)。降雨和温度是模型的驱动数据，模型采用Hamon方程[19]计算潜在蒸散发。黑河流域上游面积大、海拔高，而研究区周边仅有4个气象站，所以模型采用泰森多边形法计算平均降雨量，并同时考虑海拔梯度对温度和降雨的影响。径流量是模型率定和验证的主要数据。

2.2 模型率定算法

FLEX-Topo模型采用的参数率定算法为MOSCEM-UA(Multi-Objective Shuffled Complex Evolution Metropolis-University of Arizona)[20]。Vrugt等[20]开发了该算法(算法流程图见图3)，并将其用于参数数量、复杂程度不同的3个模型中，证明该算法的有效性和高效性。该算法已被国内外学者广泛使用[21-25]。MOSCEM-UA算法需要设置3个参数：迭代次数、复合型个数以及随机样本数。根据Vrugt等[20]的建议本研究设定的3个参数值分别为100 000、24、2 304。

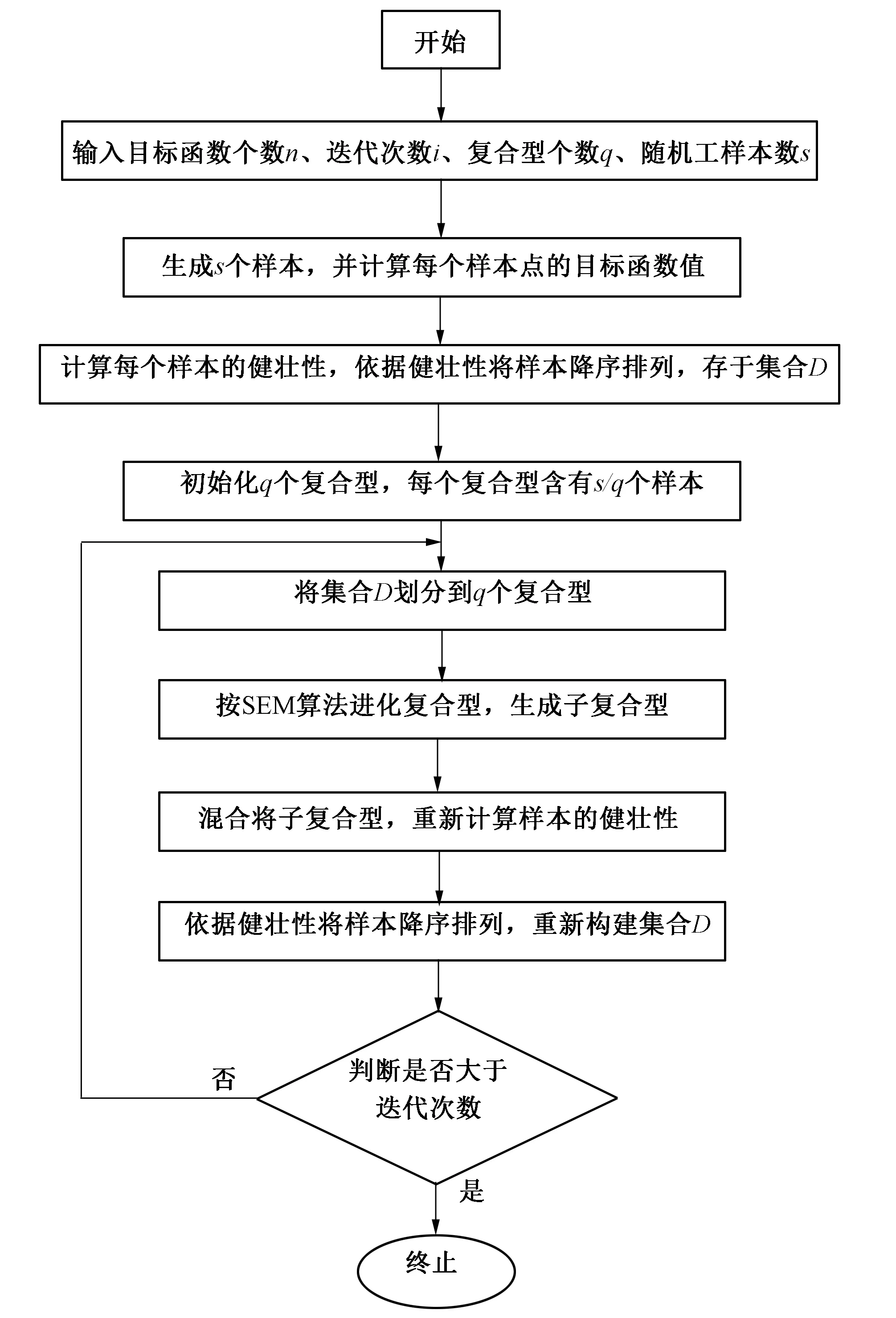
图3 MOSCEM-UA算法流程图[20]Fig.3 Flowchart of the MOSCEM-UA algorithm

2.3 研究方法

纳什系数是模型率定过程中应用最为广泛的目标函数，鉴于纳什系数的不足之处，产生了变形形式，主要包括以自然数为底的对数形式(Eln)、开平方形式(Esqrt)、绝对值形式(Eabs)和相对值形式(Erel)4种。4种变形的计算公式见表2。

FLEX-Topo模型及MOSCEM-UA算法的可靠性已经得到证明。本研究采用该模型和算法。首先，使用相同的参数范围、迭代次数(100 000)、复合型个数(24)以及随机样本数(2 304)，设定不同的目标函数(纳什系数及变形形式)进行参数率定(流程见图3)，获得5套参数。然后，将每一套参数代入模型进行验证，获得5套模拟结果。最后对5套模拟结果进行分析、比较。本研究中模型参数率定期设为1959-1978年，验证期设为1990-2006年，两阶段分别取1959和1990年为模型预热期。

表2 纳什系数及变形形式计算公式[20]Tab.2 Mathematical formulation of Nash and Sutcliffe efficiency and its modified forms

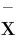
衡量模拟效果通常有两种途径，一是比较直观的图形，二是采用数值指标[5,6]。常用的图形包括水文过程图和流量频率分布曲线，从图形中可以直观地查看模拟结果。其中，水文过程图强调流量随时间的变化，而流量频率分布曲线侧重于对流量的高估与低估问题；按照有无量纲，数值指标可以分为相对指标和绝对指标两大类，其中，相对指标中应用最为广泛的是纳什系数，绝对指标包括均方根误差、平均绝对误差等。Willmott[26]指出判断模拟效果时纳什系数这一相对指标不宜单独使用。Legates等[7]通过研究表明，平均绝对误差略优于均方根误差，因此，根据Legates等[7]和Anderton等[27]的建议，在评价模型效果时选取纳什系数(E)、相关系数(r)、平均绝对误差(MAE)和平均值之差(DM)4个数值指标来衡量模拟效果。4个数值指标的计算公式见表3。

3 结果与讨论

3.1 模拟结果

根据模拟结果绘制水文过程图和流量频率分布曲线。不同目标函数验证期的模型水文过程图和流量频率分布曲线见图4和图5。图4和图5中，Qo为观测流量，Qx为以x为目标函数的模拟流量。

由图4可以看出，以纳什系数及变形形式为目标函数的模拟结果中，模拟流量基本可以反映观测流量随时间的变化，但吻合程度不同：较好的是E和Esqrt，Eln和Eabs次之，Erel最差。流量频率分布曲线反映模型对涨水段、洪峰、退水段和基流等的模拟效果。由图5可以看出，对于洪峰流量，E出现高估，而Eln、Esqrt和Eabs较E略好，Erel则低估了洪峰流量；对于基流，各个目标函数的模拟效果相似，均低估了基流流量；涨水段和退水段除Erel最差外，E、Eln、Esqrt和Eabs表现差别不大，均小于观测值。

表3 3个数值指标的计算公式Tab.3 Mathematical formulation of the three numerical criterion

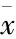
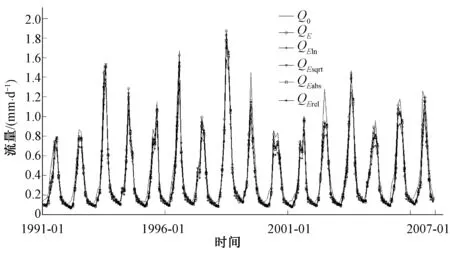
图4 验证期莺落峡水文过程图Fig.4 Hydrograph of validation period of Yingluoxia

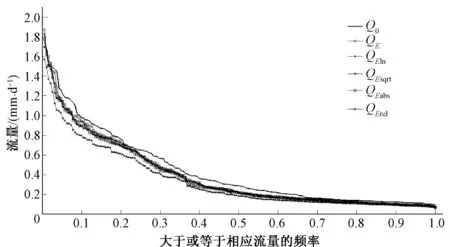
图5 验证期莺落峡流量频率分布曲线Fig.5 Flow duration curve (FDC) of validation period of Yingluoxia

虽然水文过程图和流量频率分布曲线可以直观地看出模拟结果，但整体模拟效果难以客观地直接衡量。因此，本文计算了5套模拟结果的4个数值指标，计算结果见表4。

从表4中可以看出：①4种变形形式的模拟结果中，相关系数一列的值相差不大；其余三列除Erel最差外，Eln、Esqrt和Eabs相差很小，Esqrt在各个数值指标中均为最优；②E与Esqrt相比，相关系数有所提高，这表明Esqrt较E更能反映流量的动态变化，而其余指标差别很小；③5个模拟结果中，Erel的各数值指标值均为最差；④5个模拟结果中，平均值之差一列均为正数，表明模拟结果均低估了总体水量。

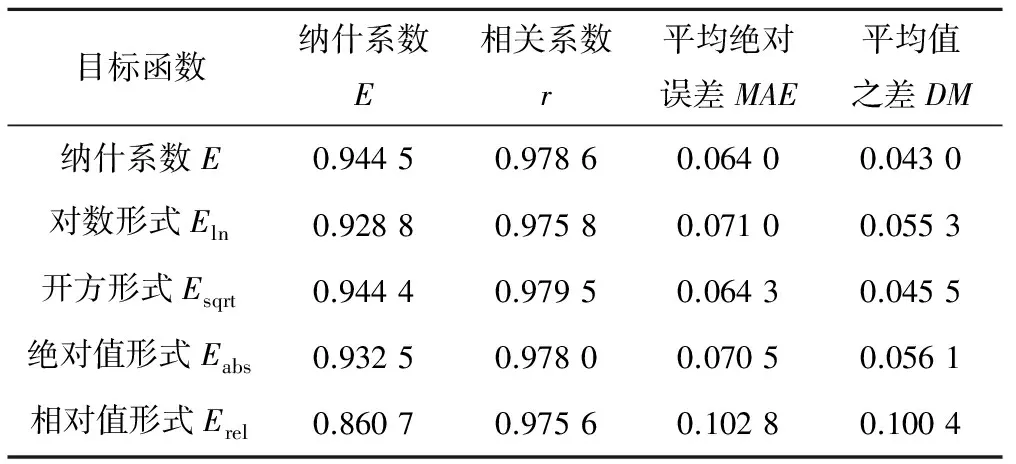
表4 不同目标函数的数值指标Tab.4 Numerical criterionof different objective functions

3.2 结果分析与讨论

Legates等[7]指出，纳什系数的计算公式采用平方形式，导致洪峰流量的影响过大，即纳什系数对洪峰流量过于敏感、忽视基流，这是欠妥的。为了解决这一问题，产生了对数形式、开方形式、绝对值形式、相对值形式。

绝对值形式的纳什系数改变了计算公式中采用的平方形式(见表2)。Legates等[7]建议使用绝对值形式的纳什系数，因为平方形式将模拟流量与观测流量的差值放大，而绝对值形式将赋予两者差值相同的权重，因此减小了洪峰流量的影响。对数形式、开方形式和相对值形式则采用另一种方式：改变流量的绝对大小(见表2)。因为计算公式中采用这种处理，就降低了洪峰流量的影响。Pushpalatha等[5]、Krause等[6]、Houghton-Carr[11]、Oudin等[12]、Kim等[13]研究证明这些变形降低了纳什系数对洪峰流量的敏感性。董磊华等[28]比较了对数均方误和平方根均方误为目标函数的模拟结果，文章指出：由对数函数曲线(y=lnx)和开方函数曲线(y=x1/2)可知，x值越小，y值递增的梯度越大，同理，流量值越小模拟流量与实测流量的误差放大越大，因此对数形式和开方形式削弱了洪峰流量的影响、增强基流流量作用。Krause等[6]提出了基于相对偏差的纳什系数计算方式，即相对值形式。通过这种变形，观测流量和模拟流量的差值用相对偏差来衡量，从而减小洪峰流量的影响、增强基流流量的影响。但是，从结果来看，这种变形形式的模拟效果在所有变形形式中最差。

上述研究表明变形形式弥补了纳什系数对洪峰流量过度敏感这一不足。然而，本研究发现，变形形式对基流流量的模拟并不理想。造成这一结果的原因可能有两个方面：一是观测误差的存在，包括降雨、温度、径流的观测误差；二是纳什系数计算公式中参考值为平均流量。对于季节流量波动较小的流域，选择平均值为参考值是合适的，但是对于流量波动大的流域则有待商榷。

4 结 语

本研究通过设定不同的目标函数，从纳什系数、相关系数、平均绝对误差和平均值之差4个指标评估模拟效果。对比各个目标函数验证期的水文过程图、流量频率分布曲线和数值指标，可以看出以相对值形式为目标函数的模拟结果最差，而以纳什系数和开方形式为目标函数的模拟结果最好；综合比较以纳什系数和开方形式为目标函数的模拟结果，两者的数值指标差别很小，但前者会明显高估洪峰流量，后者的相关系数更高，更能反映流量的动态变化。整体来讲，当选择纳什系数及其变形形式为目标函数时，开方形式的模拟效果最好。

尽管如此，5个目标函数的模拟结果均低估了基流流量，同时，也低估了整体水量。造成这一结果的原因可能有两个方面：一是观测误差；二是计算公式中参考值选择为平均流量。鉴于观测技术的限制以及观测误差存在的必然性，建议对纳什系数公式中参考值的选择开展进一步研究以提高模拟效果。

□

[1] 徐宗学,包为民,谢正辉,等. 水文模型[M].北京: 科学出版社, 2009.

[2] 刘金涛, 冯 杰, 张佳宝. 分布式水文模型在流域水资源开发利用中的应用研究进展[J]. 中国农村水利水电，2007,(2):142-144.

[3] Muleta M K. Model performance sensitivity to objective function during automated calibrations [J].Journal of Hydrologic Engineering, 2012,17(6):756-767.

[4] Vrugt J A, Gupta H V, Bouten W, et al. A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters [J]. Water Resources Research, 2003,39(8):1 201.

[5] Pushpalatha R, Perrin C, Moine N L, et al. A review of efficiency criteria suitable for evaluating low flow simulations [J]. Journal of Hydrology, 2012,420-421:171-182.

[6] Krause P, Boyle D P, Bäse F. Comparison of different efficiency criteria for hydrological model assessment [J]. Advances in Geosciences, 2005,5(5):89-97.

[7] Legates D R, Gregory J, Mccabe JR. Evaluating the use of ‘goodness-of-fit’ measures in hydrologic and hydrologic model validation [J].Water Resources Research, 1999,35(1):233-241.

[8] Gan T Y, Dlamini E M, Biftu G F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modelling [J]. Journal of hydrology, 1997,192:81-103.

[9] Wöhling T, Samaniego L, Kumar R. Evaluating multiple performance criteria to calibrate the distributed hydrological model of the upper Neckar catchment [J]. Environmental Earth Sciences, 2013,69(2):453-468.

[10] Schaefli B, Gupta H V. Do Nash value have value? [J]. Hydrological Processes, 2007,21:2 075-2 080.

[11] Houghton-carr H A. Assessment criteria for simple conceptual daily rainfall-runoff model [J]. Hydrological Sciences, 1999,44(2):237-261.

[12] Oudin L, Aneréassian V, Mathevet T, et al. Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations [J]. Water Resources Research, 2006,42(7):887-896.

[13] Kim H S, Lee S. Assessment of a seasonal calibration technique using multiple objectives in rainfall-runoff analysis [J].Hydrological Processes, 2014,28:2 159-2 173.

[14] Savenije H H G. HESS Opinions “Topography driven conceptual modelling (FLEX-Topo)”[J]. Hydrology and Earth System Sciences, 2010,14:2 681-2 692.

[15] Gao H, Hrachowitz M, Fenicia F, et al. Testing the realism of a topography-driven model (FLEX-Topo) in the nested catchments of the Upper Heihe, China[J].Hydrology and Earth System Sciences, 2014,18:1 895-1 915.

[16] Rennö C D, Nobre A D, Cuartas L A, et al. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environment in Amazonia [J]. Remote Sensing of Environment, 2008,112:3 469-3 481.

[17] Nobre A D, Cuartas L A, Hodnett M, et al. Height Above the Nearest Drainage-a hydrologically relevant new terrain model [J]. Journal of Hydrology, 2011,404:13-29.

[18] Gharari S, Hrachowitz M, Fenicia F, et al. Hydrological landscape classification: investigating the performance of HAND based landscape classifications in a central European meso-scale catchment [J]. Hydrology and Earth System Sciences, 2011,15:3 275-3 291.

[19] Hamon W R. Estimating potential evapotranspiration [J]. Journal of the Hydraulics Division-Asce,1961,87:107-120.

[20] Vrugt J A, Gupta H V, Bastidas L A, et al. Effective and efficient algorithm for multiobjective optimization of hydrologic model [J]. Water Resources Research, 2003,39(8):1-19.

[21] Schoups G, Addams C L, Gorelick S M. Multi-objective calibration of a surface water-groundwater flow model in an irrigated agricultural region: Yaqui Valley, Sonora, Mexico [J]. Hydrology and Earth System Sciences, 2005,9:549-568.

[22] Tang Y, Reed P, Kollat J. Parallelization strategies for rapid and robust evolutionary multiobjective optimization in water resources applications [J]. Advances in Water Resources,2007,30(3):335-353.

[23] Parajka J, Merz R, Blöschl G. Uncertainty and multiple objective calibration in regional water balance modelling: case study in 320 Austrian catchments [J]. Hydrological Processes, 2007,21(4):435-446.

[24] Fenicia F, Solomatine D P, Savenije H H G, et al. Soft combination of local models in a multi-objective framework [J]. Hydrology and Earth System Sciences, 2007,11:1 797-1 809.

[25] 王宇晖,雷晓辉,蒋云钟.基于MOSCEM-UA算法的水文模型参数优化[J].人民长江，2010,41(19):95:99.

[26] Willmott C J. On the validation of models [J]. Physical Geography, 1981,2(2):184-194.

[27] Anderton S, Latron J, Gallart F. Sensitivity analysis and multi-response, multi-criteria evaluation of a physically based distributed model [J]. Hydrological Processes, 2002,16:333-353.

[28] 董磊华, 熊立华. 水文模型中不同目标函数的影响比较分析[J].水文，2009, 29(3):24-27.