基于扁平衰减三角形结构元素的滚动轴承故障诊断

龚廷恺

(南昌航空大学 飞行器工程学院，南昌 330063)

0 引言

滚动轴承是旋转机械常用的零部件。由于长时间处于变负载状况下运行，滚动轴承外圈、内圈和滚动体上常会出现磨损、点蚀和裂痕等故障，这些问题是导致机器故障的主要诱因之一[1]。当轴承出现故障时，采集的振动信号特点是具有许多周期性冲击脉冲。这些脉冲的提取成为轴承故障诊断的依据。但是，这些脉冲常常被噪声所污染，因此难以提取。为了解决这个问题，急需研究一些有效的信号处理方法，即滤除噪声，提取冲击特征。

针对这一需求，许多信号处理方法被应用在滚动轴承故障诊断中。例如，包络分析、经验模态分解和小波变换[2-8]。但是，这些方法有着各自的不足，比如：包络分析中需滤除的频带范围要依据经验知识来确定；经验模态分解的缺陷在于端点效应，模式混叠和边频带特征提取较弱；小波变换的缺点是频谱泄漏、边界扭曲和小波函数需事先定义。相比于前述方法，数学形态的非线性滤波特性在故障诊断中具有更好的诊断效果[9]。数学形态方法是用一个类似探针的结构元素与原始信号进行形态特征匹配，如果两者形态特征相似则保留这些信号成分；反之，则去除。Nikolaou and Antoniadis[9]首次把数学形态应用于滚动轴承故障诊断的脉冲信号提取，他们选取了直线形、高度扁平、长度为冲击脉冲信号周期0.6倍的结构元素，成功提取出了轴承内外圈故障时的脉冲信号。文献[10-11]分别提出了基于信噪比和峭度准则的直线形结构元素长度选取方法，并应用于轴承故障诊断。李斌等[12]利用直线形多尺度结构元素进行齿轮故障诊断。文献[13]在多尺度下，应用双点直线形结构元素并结合形态谱进行滚动轴承故障分类。

上述形态学研究中所采用的结构元素都是直线形，虽然都在各自的应用中取得了较好的诊断效果，但这种结构元素与实际故障的冲击特性相似度较低。正如文献[14]中，为了获得更多的冲击特征，选用了与轴承故障时的脉冲信号相似度较高的Morlet小波作为小波母函数。为此，本研究提出扁平衰减三角形结构元素，并应用于滚动轴承故障诊断。

1 数学形态基础

数学形态是由法国科学家J.serra建立，数学形态理论基础是集合论、拓扑学、随机几何和偏微分方程等[15]，最初主要应用在图像处理领域，后来逐渐拓展到在一维信号处理。

1.1 基本形态算子

形态学有4个基础运算算子，包括膨胀运算、腐蚀运算、开运算和闭运算。他们的定义如下：

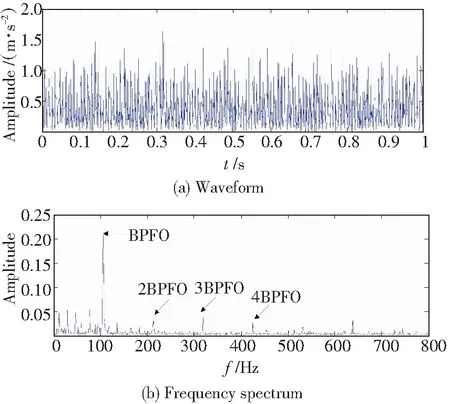
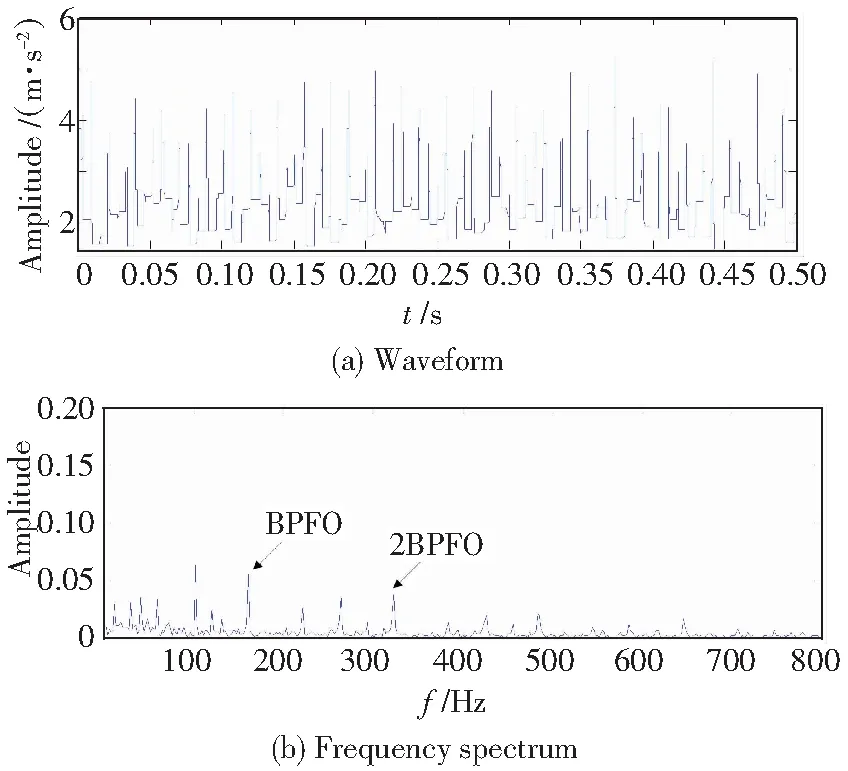
设f(n)为一维离散信号，F=(0,1,2,…,N-1)。假设s(n)为结构元素，一个离散的一维信号，定义为S=(0,1,2…M-1)，且M

(f⊕s)(n)=max{f(n-m)+s(n)}，m∈M

(1)

(fΘs)(n)=min{f(n+m)-s(n)}，m∈M

(2)

式中符号⊕和Θ分别表示膨胀算子和腐蚀算子。

开运算和闭运算的定义为：

(f。s)(n)=fΘs⊕s)(n)

(3)

(f·s)(n)=f⊕sΘs)(n)

(4)

式中符号·和。分别表示闭算子和开算子。

这4个基本算子对脉冲特征的属性为：膨胀和腐蚀算子分别能平滑正和负脉冲信号，闭和开算子分别能提取正和负脉冲。因此，这些算子对脉冲特性的属性具有单一性。

除此之外，形态学中还定义了一个基于开和闭算子的差分算子：

DIF(f)=f·g-f。g

(5)

DIF算子能同时提取正、负脉冲。

1.2 结构元素选择

结构元素作为一个参照物，其特点是相比于原始信号要简单和紧凑，便于计算和分析。结构元素具有3个属性，即形状、长度和高度。

结构元素形状的确定需根据待提取特征信号的形态特征，主要有直线形、圆形和扁平形结构元素；结构元素长度是形态滤波的一种参考依据，短的结构元素能保留特征信息，而长的结构元素滤波效果更好；结构元素高度的确定主要依据原始信号的幅值，而且这种高度计算复杂。形态应用中，结构元素的属性构造成为关键。

2 建议方法

2.1 形态算子

上述4个基本形态算子对于脉冲信号的形态运算具有单一性，即只能平滑或提取单一正或负脉冲。而实际振动信号中难以得到正、负脉冲数量的先验知识。因此根据DIF算子的双向脉冲提取特点，本研究选用DIF算子作为形态算子。

2.2 扁平衰减三角形的结构元素

如前所述，结构元素属性决定了形态计算的效果。以往研究中结构元素的选取都有各自依据，本研究以实际故障轴承的振动信号时域特点来确定结构元素的3个属性。图1显示了一个实际故障轴承的时域波形。从图中发现：脉冲信号从激发至衰减，外形上类似一个三角形，而且这些脉冲信号的幅值具有一定的对称性。根据这些特点，一种扁平衰减三角形结构元素被定义。首先，结构元素选择的高度依然选择扁平，因为确定高度因素的计算过程较为复杂，为了简化计算，设定高度为0。同时，由于实际故障信号具有对称性，因此建议的结构元素也应有相似属性。综上所述，这个扁平衰减三角形结构元素如图2所示，表1中列举了这些结构元素的操作域，即结构元素中为1的数据点将保留，为0的则被去除。这种结构元素与原始信号的外形相似度较高，因此冲击特征提取效果更好。

3 滚动轴承故障特征提取

3.1 外圈故障特征提取

为了说明所述方法的有效性，将采用电机轴承内、外圈故障的振动信号进行分析,试验平台如图3所示[16]。首先，外圈故障的相关试验参数为：转速1 790r/min，采样频率12kHz，采样时间1s。根据计算，这个外圈特征频率(BallPassingFrequencyOuterRace，BPFO)大约为107Hz。图4a中显示了这个振动信号的时域图，并且从频谱图4b中发现，故障特征因噪声较强没有提取出来。

表1 扁平衰减三角形结构元素的领域值Table 1 Neighborhood of flat attenuated triangular SEs

图1 轴承故障时域信号Fig.1 Waveform of vibration signals collected whena bearing fault occurs

图2 扁平衰减三角形结构元素Fig.2 Flat attenuated triangular SEs

图3 轴承实验台Fig.3 Testing rig for bearing

图4 轴承外圈故障振动信号Fig.4 Original vibration signals of the bearingwith an outer race fault

采用建议方法对该信号进行处理，得到的频谱图如图5b所示。这个频谱图中故障特征频率BPFO及谐波2BPFO、3BPFO、4BPFO等都明显地被提取。因此，建议的结构元素对于提取这些冲击特征是有效的。

图5 使用扁平衰减三角形结构元素的结果Fig.5 Result of using the proposed SEs applied for theouter race fault diagnosis

3.2 内圈故障特征提取

内圈故障时，电机转速1 750r/min，轴转速29.2Hz，采样频率12kHz，采样时间0.5s。依据计算，内圈故障特征频率(BallPassingFrequencyInnerRace，BPFI)约为104.5Hz。原始振动信号的时域波形如图6a所示。

图6 轴承外圈故障振动信号Fig.6 Original vibration signals of the bearingwith an outer race fault

经过建议方法处理后，所得到的频谱图如图7b。从图中可以发现：内圈故障时的特征频率BPFI及其谐波2BPFI、3BPFI和4BPFI都是可以提取的。因此，这说明使用扁平衰减三角形结构元素依然能够提取出内圈故障特征频率。

图7 使用扁平衰减三角形结构元素的结果Fig.7 Result of using the proposed SEs applied for theouter race fault diagnosis

3.3 两种方法对比

为了突出研究中所建议结构元素的优势，将其与文献[9]所提出的方法进行比较。首先，为了不失一般性，该方法中的形态算子同样选取DIF算子。结构元素长度为0.6倍的脉冲重复周期。然后，对上述2个故障信号分别进行分析。相应结果的频谱图为图8b、图9b。通过图5b与图8b，以及图7b与图9b的比较，可以发现：扁平衰减结构元素比普通扁平直线形结构元素具有更好的特征提取能力。原因如下：首先，从外形上，研究中建议的结构元素与实际故障信号的相似度较高；其次，使用建议结构元素的形态滤波效果更好。假设普通扁平结构元素为{1 1 1 1 1 1 1 1 1}，那么形态计算的操作域包含9个，而衰减扁平结构元素{0 1 0 1 0 1 0 1 0 }中，结构元素长度为9，但实际形态运算点只有4个。在这种情况下，原始信号中将会有更多的数据点被去除，滤波效果更好。因此，在使用扁平衰减三角形结构元素时，噪声抑制效果更好，故障特征提取明显。

图8 轴承外圈故障振动信号Fig.8 Result of using the proposed SEs for theouter race fault diagnosis

图9 使用扁平衰减三角形结构元素的结果Fig.9 Result of using the proposed SEs for theouter race fault diagnosis

4 结论

针对滚动轴承故障时的脉冲冲击特征提取问题，提出了基于扁平衰减三角形结构元素的形态滤波方法。实际轴承的内、外圈故障诊断表明，该方法能够提取出脉冲特征。与线性结构元素相比，这种结构元素和脉冲外形相似度较高，相同长度下形态计算具有更强的滤波能力。

[1]JardineAKS,LinD,BanjevicD.Areviewonmachinerydiagnosticsandprognosticsimplementingcondition-basedmaintenance[J].MechanicalSystems&SignalProcessing,2006,20(7):1483-1510.

[2] 潘作为,梁双印,李惊涛,等. 基于复数小波多尺度包络分析的风机滚动轴承故障特征提取[J]. 中国电机工程学报,2015,35(16):4147-4152.

[3] 张斌，王细洋. 基于小波包和EMD的谱峭度法在滚动轴承故障诊断中的应用[J]. 失效分析与预防，2015，10(5)：280-285.

[4] 武哲,杨绍普,任彬,等. 基于噪声辅助多元经验模态分解和多尺度形态学的滚动轴承故障诊断方法[J]. 振动与冲击,2016,35(4):127-133.

[5] 刘建强,赵治博,任刚,等. 基于小波包分解和集合经验模态分解的列车转向架轴承智能故障诊断方法[J]. 铁道学报,2015(7):40-45.

[6] 张旭,李超强,杨柳,等. 经验模态分解在滚动轴承故障诊断中的应用与扩展[J]. 轴承,2016(6):59-62.

[7] 胥永刚,孟志鹏,赵国亮. 基于双树复小波变换的轴承复合故障诊断研究[J]. 仪器仪表学报,2014,35(2):447-452.

[8] 贺王鹏,訾艳阳,陈彬强，等. 周期稀疏导向超小波在风力发电设备发电机轴承故障诊断中的应用[J]. 机械工程学报,2016,52(3):41-48.

[9]NikolaouNG,AntoniadisIA.Applicationofmorphologicaloperatorsasenvelopeextractorsforimpulsive-typeperiodicsignals[J].MechanicalSystems&SignalProcessing,2003,17(6):1147-1162.

[10]RajAS,MuraliN.Earlyclassificationofbearingfaultsusingmorphologicaloperatorsandfuzzyinference[J].IEEETransactionsonIndustrialElectronics,2012,60(2):567-574.

[11]DongY,LiaoM,ZhangX,etal.Faultsdiagnosisofrollingelementbearingsbasedonmodifiedmorphologicalmethod[J].MechanicalSystemsandSignalProcessing,2011,25(4):1276-1286.

[12]LiB,ZhangPL,WangZJ,etal.Aweightedmulti-scalemorphologicalgradientfilterforrollingelementbearingfaultdetection[J].ISATransactions,2011,50(4):599.

[13]ChenQ,ChenZ,SunW,etal.Anewstructuringelementformulti-scalemorphologyanalysisanditsapplicationinrollingelementbearingfaultdiagnosis[J].JournalofVibration&Control,2015,21(4):765-789.

[14]QiuH,LeeJ,LinJ,etal.Waveletfilter-basedweaksignaturedetectionmethodanditsapplicationonrollingelementbearingprognostics[J].JournalofSound&Vibration,2006,289(4):1066-1090.

[15]SerraJ.Imageanalysisandmathematicalmorphology[M].AcademicPress,1982.

[16]CaseWesternReserveUniversityBearingDataCenter.Bearingdatacenterfaulttestdata[EB/OL]. [2016-7-01].http://csegroups.case.edu/bearingdatacenter/home