饱和土-隧道动力响应的2.5维有限元-边界元耦合模型1)

何 超周顺华 狄宏规 肖军华

(同济大学道路与交通工程教育部重点实验室，上海201804)

饱和土-隧道动力响应的2.5维有限元-边界元耦合模型1)

何 超2)周顺华 狄宏规 肖军华

(同济大学道路与交通工程教育部重点实验室，上海201804)

针对饱和土中异形隧道的三维动力响应问题，建立了2.5维有限元与边界元耦合模型.将隧道结构视为弹性体，采用2.5维有限元建立隧道模型;将地基土视为饱和多孔介质，采用2.5维边界元建立饱和土体模型.借助组合辅助问题基本解消除了边界积分方程的奇异性.利用饱和土与隧道接触面的位移、面力连续和完全透水或完全不透水边界条件，实现2.5维有限元和边界元模型的耦合求解.模型具有计算效率高、适用范围广的优点.通过与完全透水和完全不透水边界条件下轴对称问题的半解析解以及单相介质的2.5维有限元与边界元耦合模型对比，验证了本文模型的正确性.最后利用该模型计算了饱和土体中类矩形隧道在移动载荷作用下的三维动力响应，分析了不同土体渗透性下位移及孔隙水压力沿隧道轴向、环向和深度的分布规律.结果表明：(1)孔隙水压力随土体渗透性增大而显著减小，位移受土体渗透性影响小；(2)位移及孔隙水压力在隧道环向主要分布在距载荷作用点两侧约2 m的范围内；(3)孔隙水压力沿深度的衰减比土体位移快，且孔隙水压力和轴向位移沿深度的分布受土体渗透性影响大.

饱和土，异形隧道，动力响应，有限元与边界元耦合，Fourier变换

引言

随着地铁建设的快速发展，一方面，软土地区(如长三角、珠三角等沿海地区)地铁隧道的长期沉降问题越发凸显，影响线路运营和维修费用[1-4].其中地铁运行引起的车载累积沉降占比大，而列车运行引起的地基动应力计算是预测车载累积沉降的基础；另一方面，地铁运行引起的环境振动问题日益严重，而环境振动问题的关键在于地铁运行引起的自由场振动预测.而无论是地基动应力计算还是自由场振动预测均是土与隧道的动力相互作用问题.

对此，部分学者将地基考虑为单相介质进行求解.Mettrikine等[5]将隧道假定为欧拉梁，利用解析法探讨了隧道及地表的振动响应.Forrest等[6]构建了三维的隧道与地基振动分析模型，即PiP模型.随后，Forrest等[7]和Hussein等[8]又将PiP模型与浮置板轨道模型进行耦合求解分析.

在数值法上，Chua等[9]建立了二维有限元模型，分析地铁运行引起地表建筑的动力响应.Gardien等[10]建立了三维有限元模型，考虑了振动产生与传播的整个过程.而刘维宁等[11]、宫全美等[12]和钱春宇等[13]利用车辆-轨道-隧道-地层系统的三维有限元模型，分析地铁运行引起的三维动力响应.而利用地铁隧道及土层在隧道纵向上的一致性，谢伟平等[14]和Bian等[15]采用2.5维有限元法，研究了列车运行引起的隧道与地基振动.2.5维有限元法又称波数有限元法，通过对三维计算域进行纵向坐标Fourier变换，可实现在波数域内对横向二维区域进行计算，最后将波数域内求解的结果通过反变换得到三维空间中的解答.该法求解土与隧道动力相互作用问题的优点在于仅需对隧道和土层进行二维离散，便可得到三维响应，较三维有限元计算效率高.

而考虑到有限元仍需对结构及土层进行离散，且需要采用人工边界截断无限域，存在一定的计算误差.Sheng等[16]提出了2.5维有限元与边界元耦合模型，用有限元模拟结构，用边界元模拟土体，计算了地下隧道的振动响应.Franc¸ois等[17]和Galv´ın等[18]又在此基础上采用了层状半空间问题的基本解和正则化的边界积分方程，提高了计算精度和效率.Degrande等[19]则提出了周期性有限元与边界元耦合模型，研究隧道和地基的动力相互作用问题. Gupta等[20]比较了PiP模型和周期性有限元与边界元耦合模型，指出有限元与边界元耦合模型能考虑异形断面隧道.

然而，我国沿海经济发达地区，如长江三角洲、珠江三角洲和渤海湾等均属饱和土地基，饱和土地基在地铁载荷作用下产生的动力响应与单相介质不同，采用饱和多孔介质理论进行研究更合理.对此，Senjuntichai等[21]得到了饱和土中圆柱孔洞内表面作用轴对称载荷和流体压力下的瞬时响应解答；刘干斌等[22]研究了黏弹性饱和土中隧道受轴对称载荷和流体压力作用下的响应问题；黄晓吉等[23]和Hasheminejad等[24]分别研究了饱和土与衬砌完全透水和完全不透水条件下环向移动载荷作用下系统的响应，但上述模型均针对轴对称问题.

为获得土与隧道系统的三维动力响应，曾晨等[25-26]在PiP模型基础上结合Biot理论，研究了简谐载荷及移动载荷作用下饱和土和隧道的三维动力响应；狄宏规等[27]用双层圆柱壳模拟隧道和壁后注浆层，分析了注浆层对动应力的影响.邹炎[28]用三维有限元方法分析了饱和土中箱型隧道的地震反应；而高广运等[29]和袁宗浩等[30]则采用2.5维有限元模型，研究了列车载荷作用下隧道和饱和土地基的三维动力响应.

由以上文献分析可知，研究饱和土与隧道的三维动力相互作用问题的方法有修正的PiP模型[25-27[28-30]，前者属于半解析法，计算效率高，然而受假设限制，仅能分析圆形隧道的振动响应.而有限单元法在计算土与隧道的三维动力相互作用问题上计算耗时长，且会因截断无限域而导致一定的计算误差.

对此，本文基于弹性理论和Biot理论，建立了2.5维有限元与边界元耦合模型.采用2.5维有限元法建立隧道模型，采用2.5维边界元法建立饱和土体模型.利用饱和土与隧道接触面的边界条件，实现2.5维有限元和2.5维边界元的耦合求解.模型能够考虑隧道几何断面和载荷的非对称性，且只需对隧道结构进行二维离散，计算效率高.通过与现有计算模型对比，验证了本文模型的正确性.最后利用该模型，对饱和土体中的类矩形隧道在移动载荷作用下的三维动力响应问题进行了分析.

1 隧道的2.5维有限元模型

将隧道视为弹性体，对于作用在隧道结构Ωt上的虚位移δt，应用虚功原理得

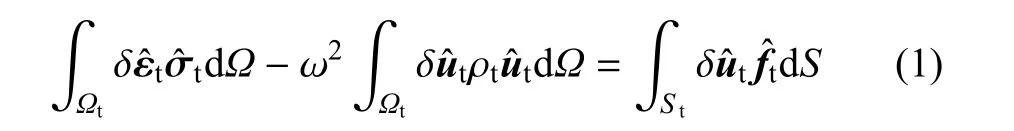
式中，顶标“∧”表示变量位于频域内；St为Ωt对应的边界；和为隧道的位移张量和应力张量；为隧道所受外载荷；为虚应变；ω为圆频率；和iz为基向量；λt,µt为隧道的Lam´e常数；ρt为隧道密度.

弹性体的物理方程和几何方程为

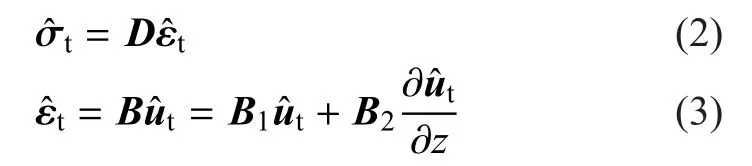
式中，D为弹性矩阵，B1和B2为应变矩阵

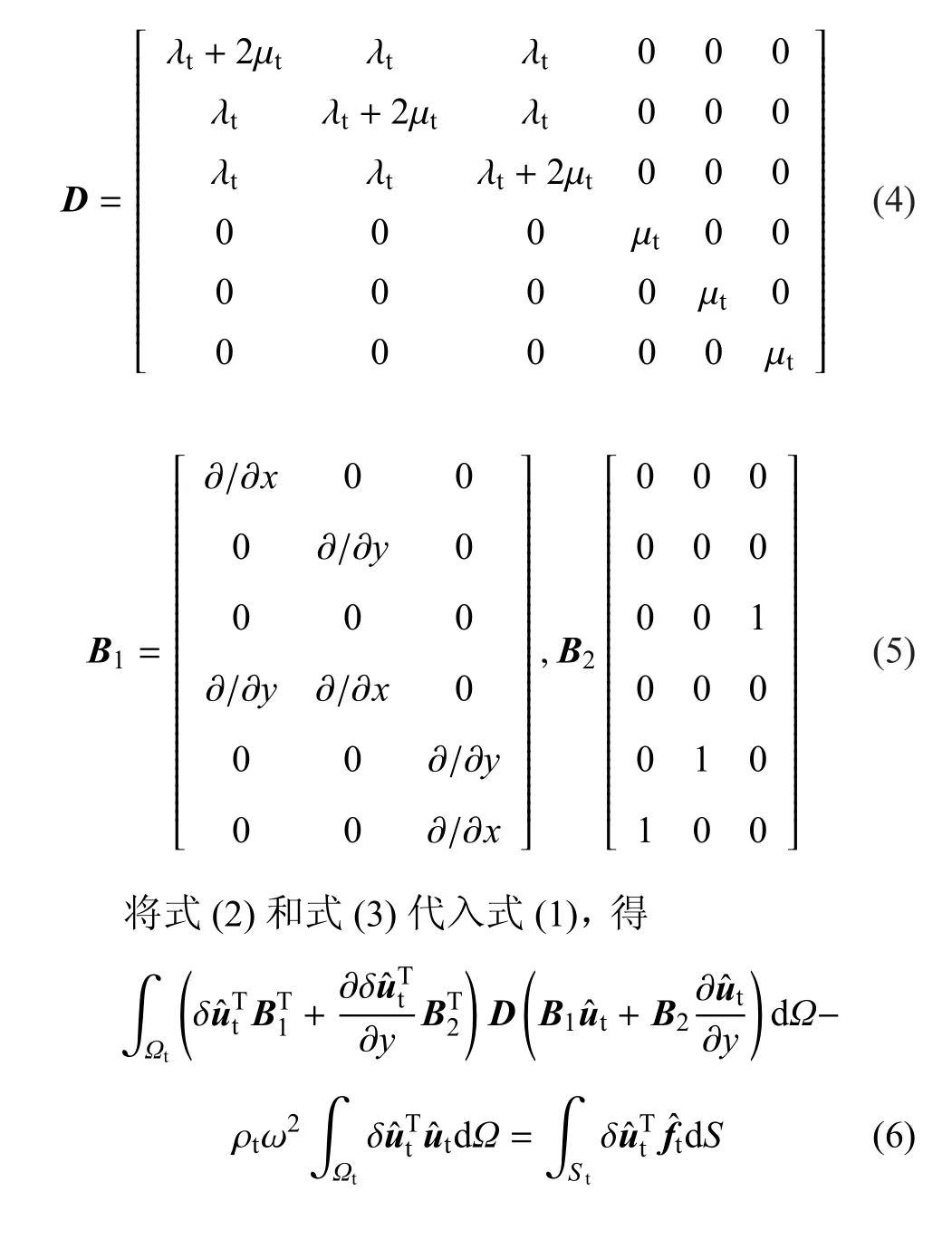
假设隧道结构沿z向(隧道轴线方向)无限长，且横断面At保持一致.对位移t(x,ω)在xy平面内进行离散，得

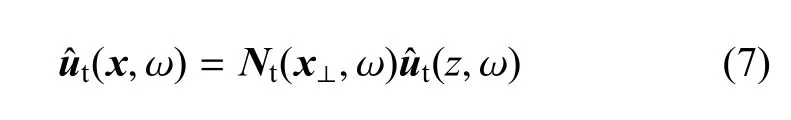
式中，Nt(x⊥)为形函数;为坐标在xy平面的分量.用相同的形函数表示虚位移

将式(7)代入式(6)，并对式(6)在纵向z向进行Fourier变换

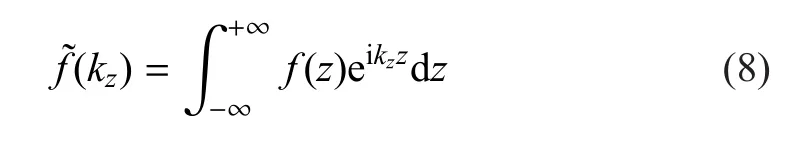
式中，顶标“～”表示变量位于频率-波数域；kz表示沿z方向的波数.

最终获得离散后的2.5维有限元方程

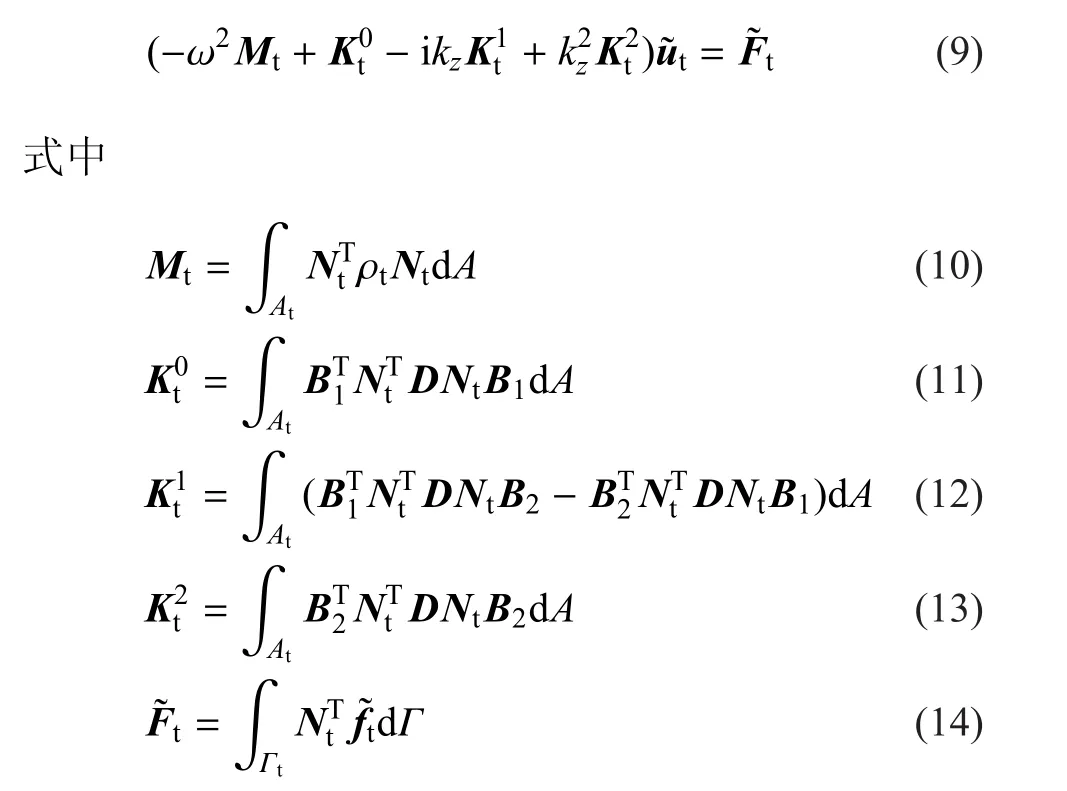
2 饱和土体的2.5维边界元模型

2.1 饱和土体的2.5维边界积分方程

根据Biot理论[31-32]，饱和多孔介质的物理方程为

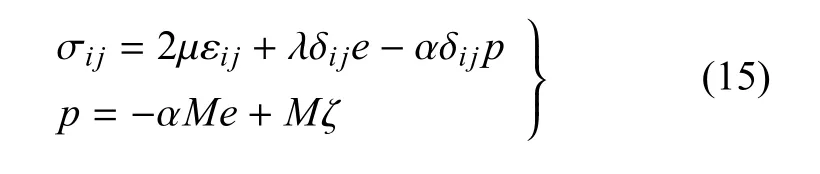
式中，σij为土体总应力；εij为土体固相应变；e=ui,i；ζ=-wi,i为单位体积的流体体积变化量；w为孔隙流体相对固体骨架的平均位移；λ,µ为土骨架的Lam´e常数；α,M为Biot常数.

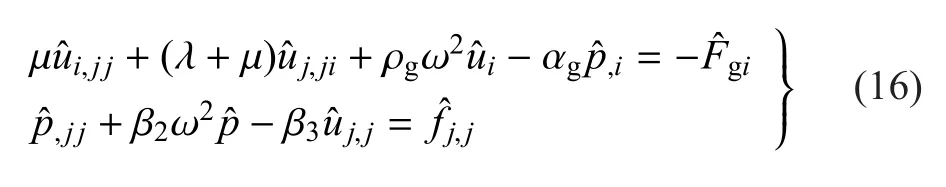
式中，ρg=ρb-β4;αg=α-β4;β1=M/(mω2-iωb);β2=1/(β1ω2);β3=ρfω2-αM/β1;β4=ρfω2β1/M；Fgi=Fi-β4fi;m=a∞ρf/φ;b=η/k反应土体黏性耦合的参数，η为流体的动力黏滞系数，k为流体的渗透系数；a∞为曲折度；ρb=(1-n)ρs+nρf，ρb为饱和土体密度，ρs为土骨架密度,ρf为孔隙流体密度；n为孔隙率；Fi和fi为饱和土以及孔隙流体的体力项.

考虑饱和土体任意2个状态(状态1和状态2)，根据互易定理可得

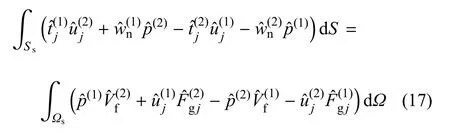
式中，Ωs为饱和土区域，Ss为Ωs对应的边界；为边界上的面力；为孔隙流体相对于土骨架的位移沿边界外法线方向的分量，nj为边界外法线的方向余弦；

假设状态1为真实状态，并忽略体力，状态2的位移、孔隙水压力和应力是由饱和全空间内作用一单位点载荷或者单位流相点源引起的.则当在点x处沿i轴(i=1,2,3，对应于x,y,z方向)作用单位点载荷时的饱和多孔介质Somigliana等式为

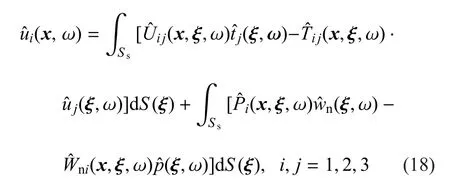
式中，ξ=ξ1ix+ξ2iy+ξ3iz，为场点坐标.

同理，当单位流相点源作用于点x处时，饱和多孔介质的Somigliana等式为

为推导方便，定义广义位移、广义面力向量和广义格林函数

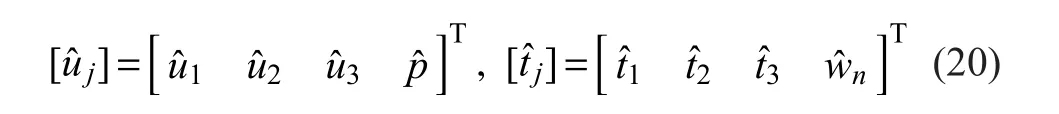
根据文献[33]的方法，当载荷的作用点向边界无限趋近时，可得到饱和多孔介质在频域内的边界积分方程

式中，积分自由项cij(x)取决于边界的几何形状，对于光滑边界[33]：cij=0.5δij.

假设饱和土体在z向上无限长且横断面保持不变.将dSs写成dΓsdz，其中Γs为饱和土在xy平面内的边界，对空间坐标z进行式(8)所示的Fourier变换，最终可获得饱和多孔介质的2.5维边界积分方程

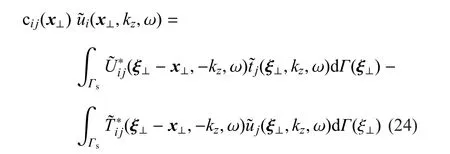
2.2 移动载荷问题的2.5维边界积分方程

当载荷以频率ω0、恒定速度v沿z轴移动时，引起的土体响应可表达为

对式 (25)进行时间t和空间坐标z的双重Fourier变换，可得

式中

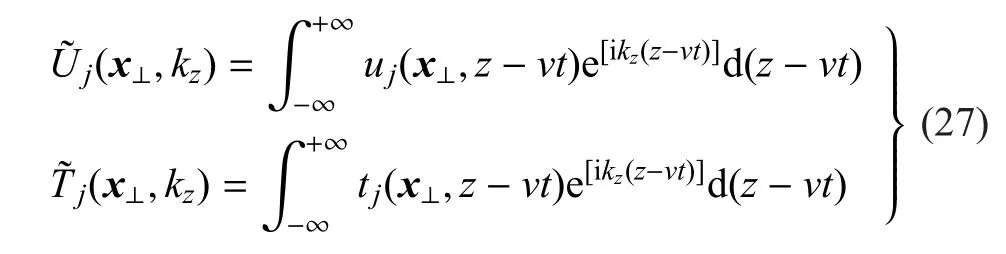
将式(27)代入式(24)，可得移动载荷作用下饱和土体的2.5维边界积分方程

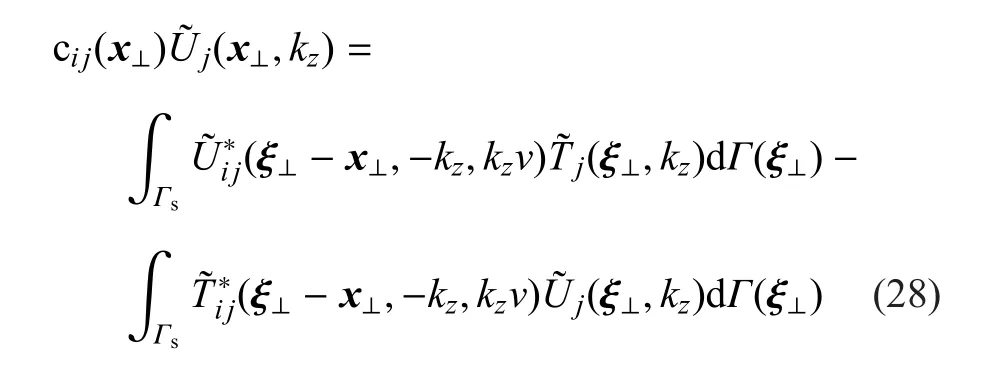
2.5 维有限元方程式(9)适用于移动载荷问题，只需将方程中的ω改为ω0+kzv即可.

2.3 边界积分方程的奇异性处理

当场点ξ⊥趋于源点x⊥时，式(24)中的格林函数存在奇异性.对此，基于动态和静态格林函数在源点处的奇异性同阶，可借助组合辅助问题基本解来消除此奇异性.

辅助问题包括弹性静态Kelvin解与Laplace方程解，辅助问题与原问题具有相同的边界，但外法线方向相反.假设辅助问题的位移为刚体平动位移，则辅助问题在边界上的应力为0，故对应的边界积分方程为

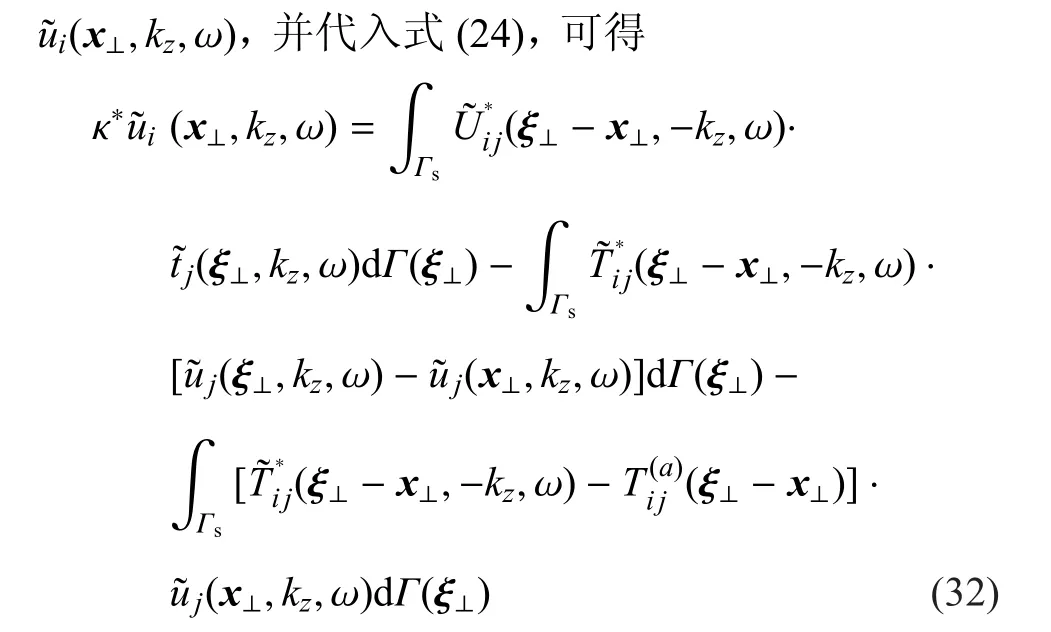
由于式(32)中动态和静态格林函数在源点处的奇异性同阶，因此上述积分中格林函数的奇异性被消除.

2.4 2.5维边界元离散

将边界Γs离散为Ne个1维等参单元，每个单元有Nn个节点.并保持在饱和土与隧道接触面上，两者的结点划分保持一致，则单元位移和面力可表示为

将式(33)代入式(32)便可得到离散后的2.5维饱和土体边界元方程

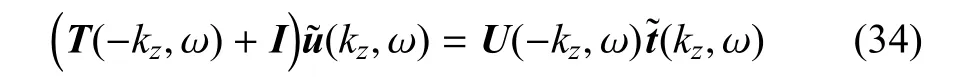
式中，U(-kz,ω)和T(-kz,ω)为边界单元系统矩阵，由式(32)中的积分计算确定，I为式(32)中的积分自由项.

3 2.5维有限元与边界元耦合模型

设有限元区域和边界元区域公共边界上的节点位移、面力、孔隙水压力、孔隙流体相对土骨架的位移沿边界外法线方向的分量和节点力分别用uI，tI，pbeI，wnbeI和FI表示.有限元区域其余节点的位移和节点力用ufeR和FfeR表示.边界元区域其余节点的广义位移和面力用ubeR和tbeR表示.

为研究饱和土与隧道的动力相互作用，对饱和土与隧道接触面引入如下边界条件：

（1）饱和土与隧道接触面位移、面力连续；

（2）饱和土与隧道接触面的水力条件考虑完全透水和完全不透水两种情况，完全透水条件下，隧道与饱和土接触面处的孔隙水压力为零，即：pbeI=0；完全不透水条件下，则孔隙流体相对土骨架的位移沿边界外法线方向的分量为零[36]，即wnbeI=0.

然后对有限元节点进行重新排列，使得2.5维有限元方程式(9)写成分块形式

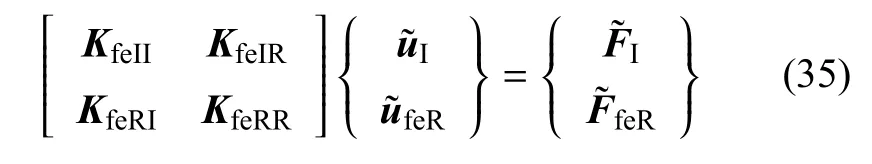
同理，对边界元自由度进行重新排列，使得2.5维边界元方程式(34)写成分块形式

式中，对于完全透水条件：ubeI=wnbeI；对于完全不透水条件：ubeI=pbeI.

有限元区域和边界元区域在公共界面上的相互作用力为面力.在边界元中，该面力被表达为节点面力的形式，而在有限元中，该面力被表达为等效节点力的形式.对此，利用虚功原理，可得有限元中的等效节点力与边界元中的节点面力之间的关系

结合式(35)～式(37)以及饱和土与隧道接触面的边界条件，可得2.5维有限元与边界元耦合系统方程

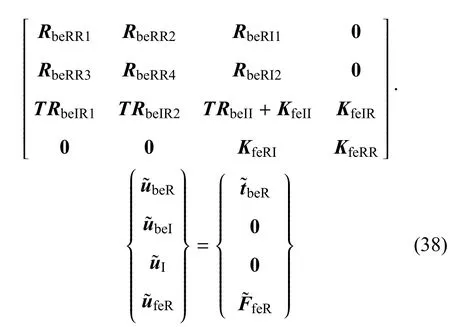
一旦利用式(38)求出边界上的位移和面力，则土体中的响应可利用离散后的式(22)进行求解.采用快速Fourier逆变换，可将频域-空间域内的解转换到时间-空间域中.

4 模型验证

4.1 与完全透水条件下的半解析解对比

为了验证本文计算模型的正确性，采用本文模型计算了文献 [23]轴对称法向载荷移动速度v=0.1v0(v0=(µ/ρb)0.5)和v=0.9v0时，r=1.5处的土体位移和孔隙水压力.其中饱和土与隧道的接触面完全透水.结果如图1和图2所示.图中z′=z-vt.由图可知，两者的计算结果吻合很好，验证了本文方法的正确性.

图1 v=0.1v0时本文计算模型与完全透水条件下的半解析解[23]的结果对比Fig.1 Comparison between presented model with the semi-analytical solution[23]of permeable interface forv=0.1v0

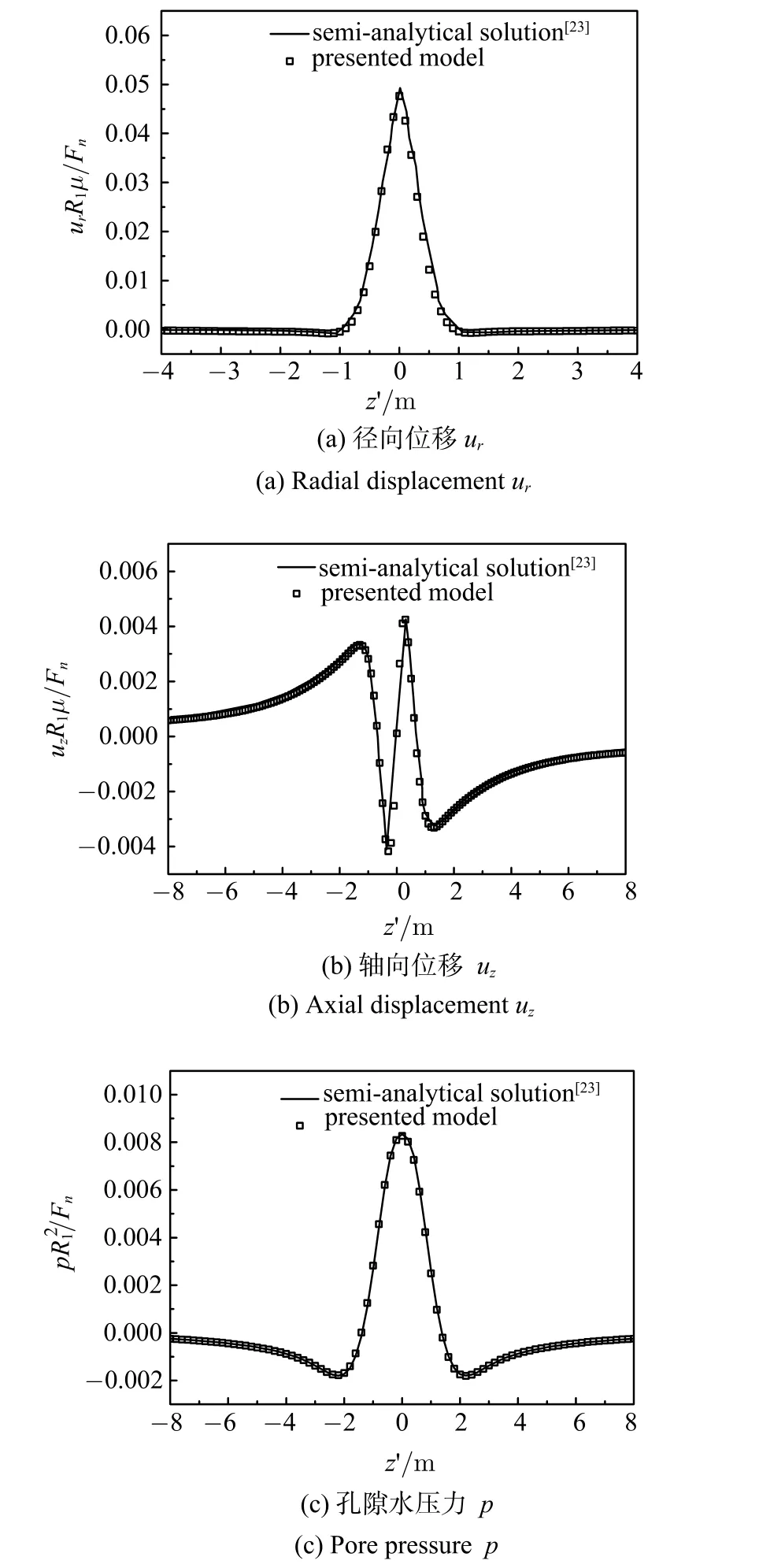
图2 v=0.9v0时本文计算模型与完全透水条件下的半解析解[23]的结果对比Fig.2 Comparison between presented model with the semi-analytical solution[23]of permeable interface forv=0.9v0

4.2 与完全不透水条件下的半解析解对比

为了验证隧道和饱和土体接触面完全不透水条件下本文计算模型的正确性，采用本文模型计算了文献[24]中轴对称法向载荷移动速度v=10 m/s、土体为软土(soft soil)时，r=R2和r=1.5R2处的径向位移ur.R2为隧道外径.结果如图3所示，两者的计算结果吻合很好，验证了本文方法的正确性.

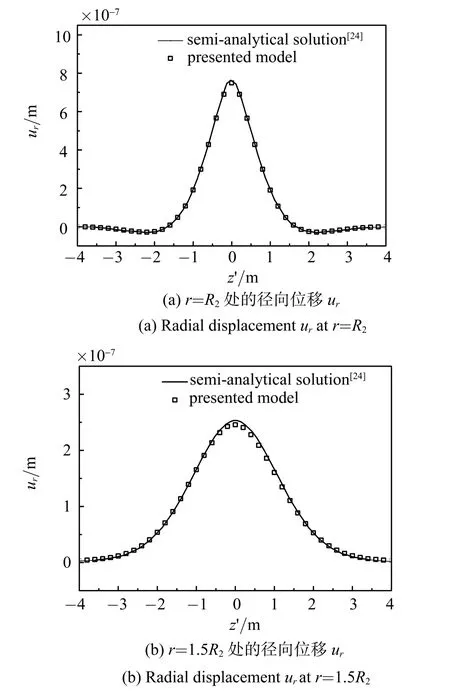
图3 本文计算模型与完全不透水条件下的半解析解[24]的结果对比Fig.3 Comparison between present model with the semi-analytical solution[24]of impermeable interface

4.3 与单相介质的2.5维耦合模型对比

将土体参数ρf,α,M,m,b取10-4，将饱和土体退化为单相介质土体.对此，采用本文模型计算了文献[16]中隧道底部作用频率f=200 Hz的竖向单位点载荷时，隧底的竖向位移.结果如图4所示，两个模型结果吻合很好，验证了本文方法的正确性.

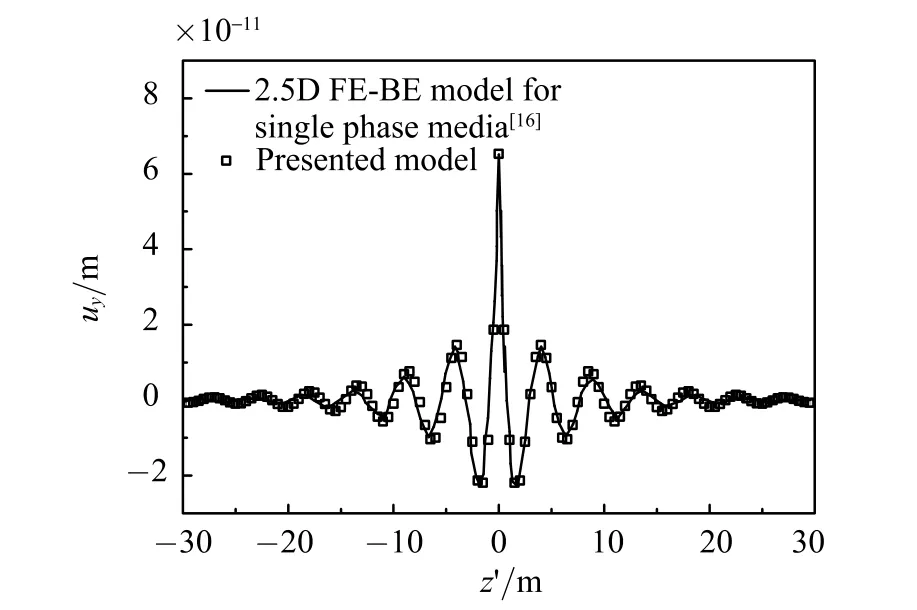
图4 本文计算模型与单相介质的2.5维有限元与边界元耦合模型[16]的结果对比Fig.4 Comparison between presented model with the 2.5D coupled FE-BE model[16]for single-phase media

5 算例和分析

相对于圆形隧道，类矩形隧道拥有更高的空间利用率，更适用于城市核心区和旧城区的地铁建设. 2015年，宁波地铁3号线类矩形盾构隧道工程正式开始，标志着我国类矩形盾构隧道迈向了一个新阶段.本文以宁波地铁3号线类矩形隧道工程为背景，采用本文模型计算饱和土地基中类矩形隧道在移动载荷作用下的动力响应.

如图5所示，隧道断面由四段圆弧组成，上下两段圆弧外径R1=15.45 m，内径R2=15 m，左右两段圆弧外径R3=3.2 m，内径R4=2.75 m，衬砌厚0.45 m，中隔柱厚0.35 m.隧道共划分为84个四边形单元.隧道及饱和土参数取值如表1和表2所示,其中隧道和土体的阻尼比取为0.05.为了研究土体渗透性对动力响应的影响，b取1010～106N·s/m4，根据定义可知，b值越小，土体渗透性越大.载荷移动速度为v=0.1v0.

图5 类矩形盾构断面形式及网格划分Fig.5 Section form and element mesh of the quasi-rectangular tunnel

表1 隧道参数Table 1 Parameters of tunnel

表2 饱和土体参数Table 2 Parameters of saturated soil

图6给出了b取不同值时，载荷作用位置下方隧底处的位移及孔隙水压力沿轴向的分布，由图6(a)和6(b)可知，土体渗透性对竖向位移uy和轴向位移uz影响小.随着b值的减小，竖向和轴向位移略有增大；竖向位移最大值位于载荷作用平面z′=0附近，呈对称分布，而轴向位移在载荷作用平面z′=0幅值为0，呈反对称分布.而由图6(c)可知，土体渗透性对孔隙水压力影响很大，随着b值由1010N·s/m4减小至106N·s/m4，孔隙水压力迅速减小，且孔隙水压力最大值的位置也向载荷前方移动.

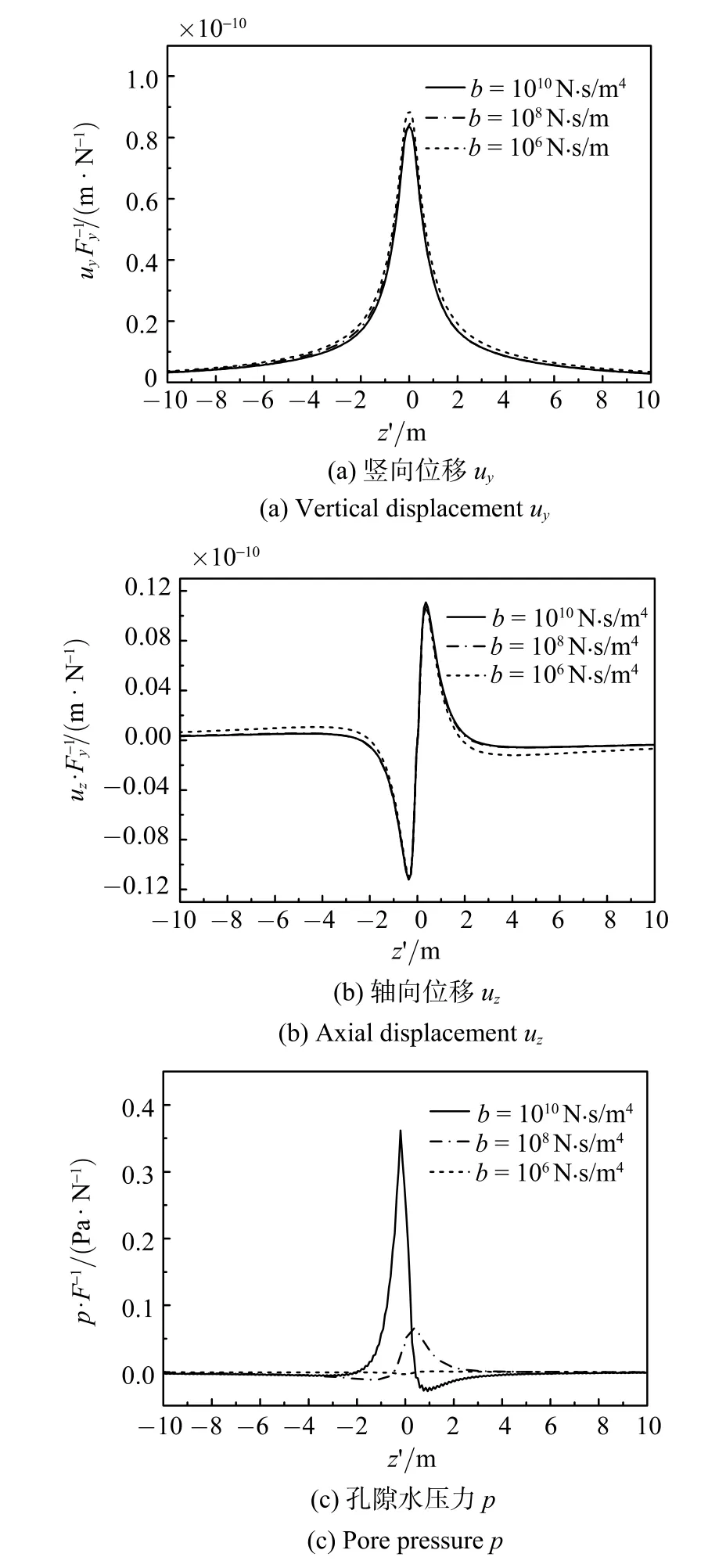
图6 载荷作用位置正下方的隧道底部处位移及孔隙水压力沿轴向分布Fig.6 Soil displacement and pore pressure at tunnel invert where loads acting varied withz′

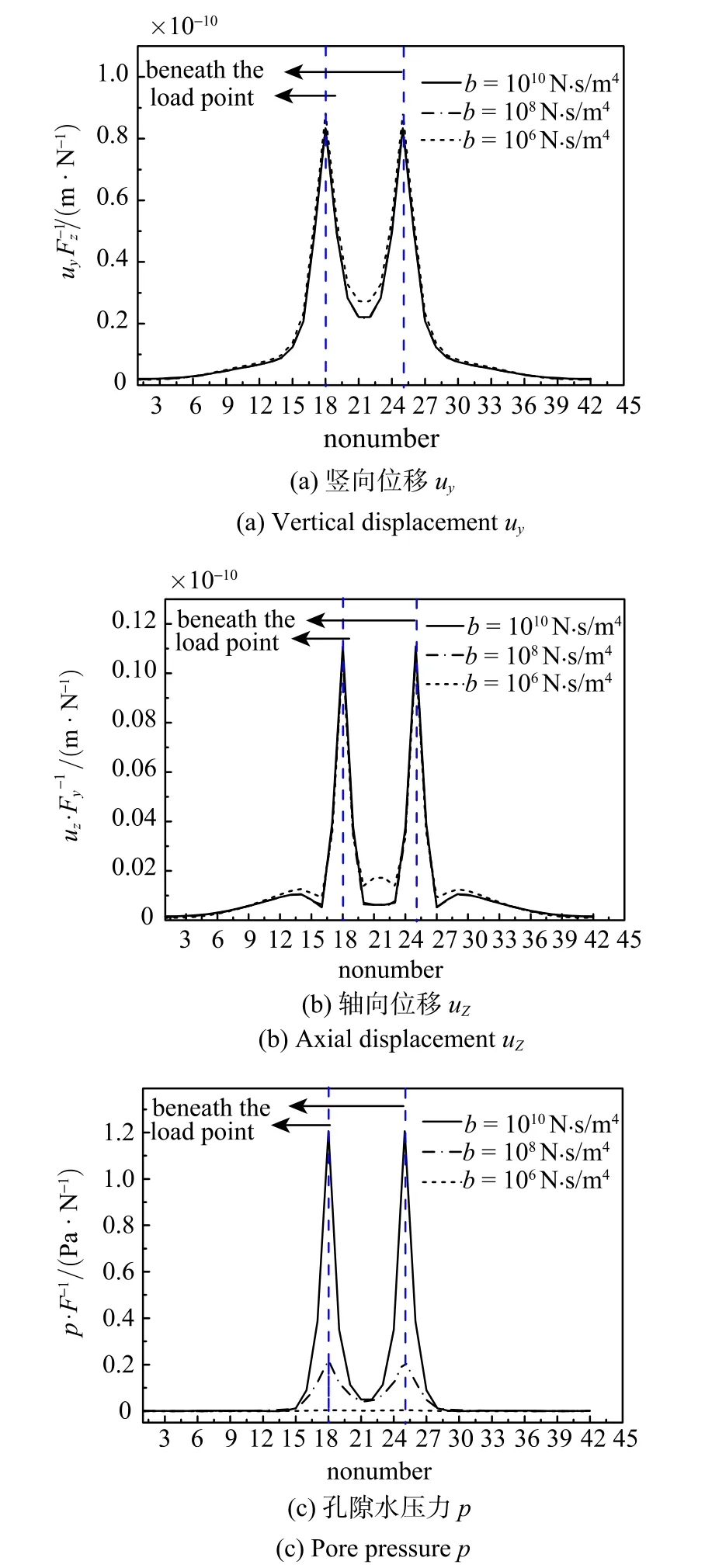
图7 不同b值时位移及孔隙水压力沿隧道环向分布Fig.7 Soil displacement and pore pressure varied with tunnel ring for dif f erent values ofb

图7给出了位移及孔隙水压力沿隧道环向的分布情况，由图可知，位移及孔隙水压力在载荷作用点两侧约2 m范围(节点15～节点28)内较大，最大值位于载荷作用点处，竖向位移和孔隙水压力仅在载荷作用点附近出现峰值，而轴向位移除载荷作用点附近的峰值外，在节点13和节点30附近还产生了峰值，但量值较小.不同b值下，位移及孔隙水压力沿隧道环向分布规律基本一致.

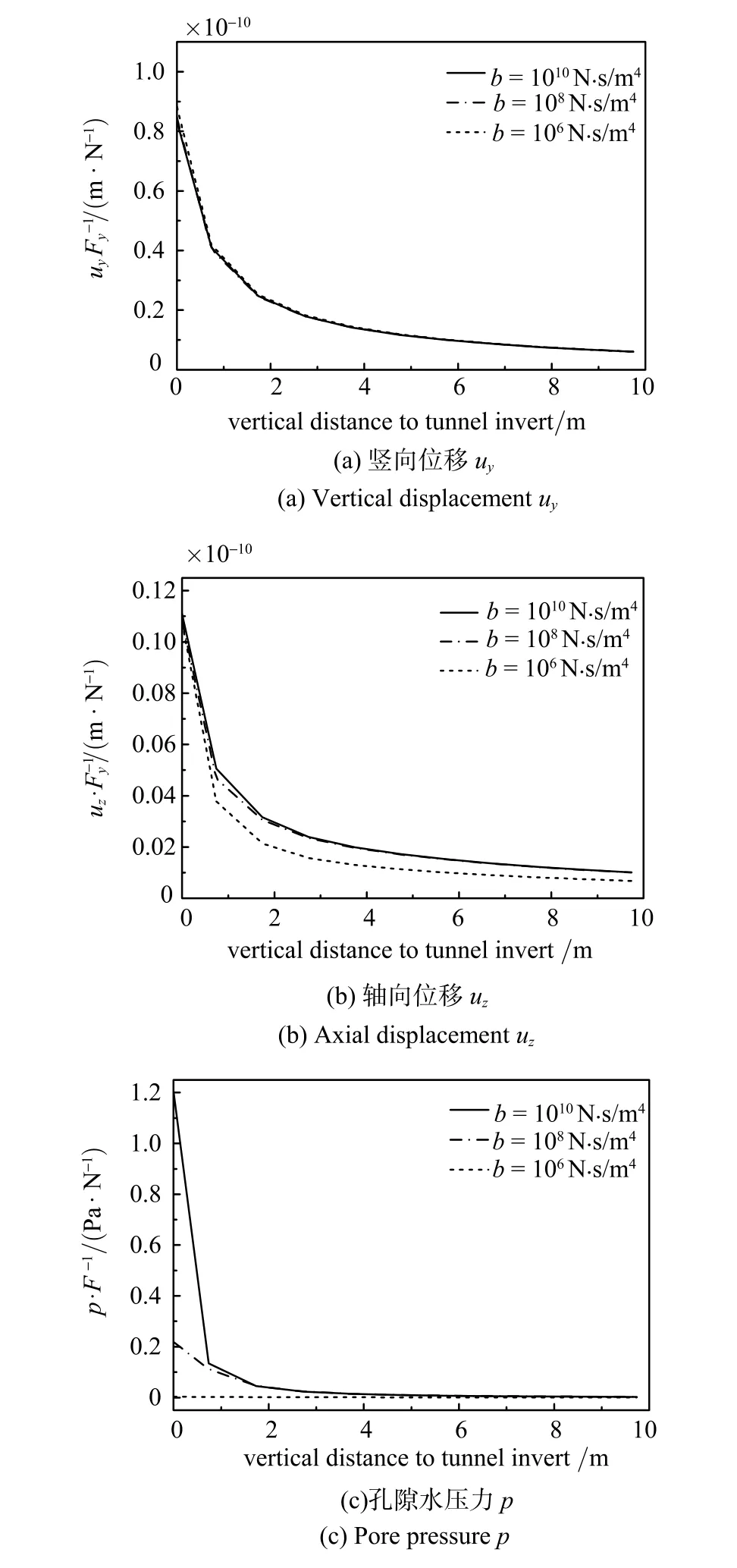
图8 不同b值时位移及孔隙水压力沿深度分布Fig.8 Soil displacement and pore pressure varied beneath the tunnel invert for dif f erent values ofb

为了分析土体不同渗透性条件下，位移及孔隙水压力随深度的衰减情况，图8给出了载荷作用位置正下方到隧道底部不同距离的点的位移和孔隙水压力分布情况.由图可知，随着距离的增加，位移和孔隙水压力逐渐衰减，竖向位移和轴向位移在距离隧底3 m左右范围内衰减了80%以上，竖向位移衰减规律基本不受土体渗透性的影响.对于轴向位移而已，当b值减小至1×106N·s/m4时，其随深度的衰减加快，说明土体渗透性对轴向位移的衰减影响较大；而孔隙水压力随深度的衰减更快，在2 m范围内基本衰减完全，随着b值的减小，相同位置处的孔隙水压力幅值迅速减小.

6 结论

本文建立了2.5维有限元与边界元耦合模型，用于分析饱和土中异形隧道的三维动力响应.模型计算效率高，能够考虑隧道几何断面和载荷的非对称性.通过与完全透水和完全不透水条件下轴对称问题的半解析解以及单相介质的2.5维有限元与边界元耦合模型对比，验证了本文模型的正确性.

以宁波地铁3号线类矩形隧道工程为背景，对饱和土体中类矩形隧道在移动载荷作用下的三维动力响应进行了计算，并根据结果分析了不同土体渗透性下位移及孔隙水压力沿隧道轴向、环向和深度的分布规律，得到如下结论：

(1)孔隙水压力随土体渗透性增大而显著减小，位移幅值受土体渗透性影响小.

(2)位移及孔隙水压力沿隧道环向主要分布在载荷作用点两侧约2 m范围内，受土体渗透性影响小.

(3)孔隙水压力沿深度的衰减比土体位移快，且孔隙水压力和轴向位移沿深度的分布受土体渗透性影响大.

1 Shen SL,Wu HN,Cui YJ,et al.Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai.Tunnelling and Underground Space Technology,2014,40(12)：309-323

2 黄大维，周顺华，宫全美等.软土地区地铁不同结构间差异沉降特点分析.同济大学学报（自然科学版）,2013,41(1)：95-100 (Huang Dawei,Zhou Shunhua,Gong Quanmei,et al.Characteristic analysis of non-uniform settlement for dif f erent structures of metro in soft soil districts.Journal of Tongji University(Natural Science), 2013,41(1)：95-100(in Chinese))

3 狄宏规，周顺华，宫全美等.软土地区地铁隧道不均匀沉降特征及分区控制.岩土工程学报,2015,37(S2)：74-79(Di Honggui,Zhou Shunhua,Gong Quanmei,et al.Dif f erential settlement of metro tunnels and its zonal control in soft deposits.Chinese Journal of Geotechnical Engineering,2015,37(S2)：74-79(in Chinese))

4 Di HG,Zhou SH,Xiao JH,et al.Investigation of the long-term settlement of a cut-and-cover metro tunnel in a soft deposit.Engineering Geology,2016,204：33-40

5 Mettrikine AV,Vrouwenvelder ACWM.Surface ground vibration due to a moving train in a tunnel：two-dimensional model.Journal of Sound and Vibration,2000,234(1)：43-66

6 Forrest JA,Hunt HEM.A three-dimensional tunnel model for calculation of train-induced ground vibration.Journal of Sound and Vibration,2006,294(4-5)：678-705

7 Forrest JA，Hunt HEM.Ground vibration generated by trains in underground tunnels.Journal of Sound and Vibration,2006,294(4-5)： 706-736

8 Hussein MFM,Hunt HEM.A numerical model for calculating vibration from a railway tunnel embedded in a full-space.Journal of Sound and Vibration,2007,305：401-431

9 Chua K,Lo KW,Balendra T.Building response due to subway train traffic.Journal of Geotechnical Engineering,1995,121(11)：747-754

10 Gardien W,Stuit HG.Modelling of soil vibrations from railway tunnels.Journal of Sound and Vibration,2003,267(3)：605-619

11 刘维宁,夏禾,郭文军.地铁列车振动的环境响应.岩石力学与工程学报,1996,15(S1)：586-593(Liu Weining,Xia He,Guo Wenjun. Study of vibration ef f ects of underground trains on surrounding environments.Chinese Journal of Rock Mechanics and Engineering, 1996,15(S1)：586-593(in Chinese))

12 宫全美,徐勇,周顺华.地铁运行载荷引起的隧道地基土动力响应分析.中国铁道科学,2005,26(4)：47-51(Gong Quanmei,Xu Yong, Zhou Shunhua.Dynamic response analysis of tunnel foundation by vehicle vibration in metro.China Railway Science,2005,26(4)：47-51(in Chinese))

13 钱春宇,郑建国,宋春雨.西安钟楼台基受地铁运行振动响应的分析.世界地震工程,2010,26(S1)：177-181(Qian Chunyu,Zheng Jianguo,Song Chunyu.Dynamic response analysis of Bell Tower foundationinducedbytrainrunningonmetroinXi′an.WorldEarthquake Engineering,2010,26(S1)：177-181(in Chinese))

14 谢伟平,孙洪刚.地铁运行时引起的土的波动分析.岩石力学与工程学报,2003,22(7)：1180-1184(Xie Weiping,Sun Honggang. FEM analysis on wave propagation in soils induced by high speed train loads,Chinese Journal of Rock Mechanics and Engineering, 2003,22(7)：1180-1184(in Chinese))

15 Bian XC,Jin WF,Jiang HG.Ground-borne vibrations due to dynamic loading from moving trains in subway tunnels.Journal of Zhejiang University—Science A:Applied Physics and Engineering, 2012,13(11)：870-876

16 Sheng X,Jones CJC,Thompson DJ.Prediction of ground vibration from trains using the wavenumber finit and boundary element methods.Journal of Sound and Vibration,2006,293(3-5)：575-586

17 Francois S,Schevenels M,Galv´ın P,et al.A 2.5D coupled FE-BE methodology for the dynamic interaction between longitudinally invariant structures and a layered halfspace.Computer Methods in Applied Mechanics and Engineering,2010,199(23-24)：1536-1548

18 Galv´ın P,Francois S,Schevenels M.A 2.5D coupled FE-BE model for the prediction of railway induced vibrations.Soil Dynamics and Earthquake Engineering,2010,30(12)：1500-1512

19 Degrande G,Clouteau D,Othman R,et al.A numerical model for ground borne vibrations from underground railway traffic based on a periodic finit element-boundary element formulation.Journal of Sound and Vibration,2006,193(3)：645-666

20 Gupta S,Hussein MFM,Degrande G.A comparison of two numericalmodelsforthepredictionofvibrationsfromundergroundrailway traffic.Soil Dynamics and Earthquake Engineering,2007,27(7)：608-624

21 Senjuntichai T,Rajapakse RKND.Transient response of a circular cavity in a poroelastic medium.International Journal for Numerical and Analytical Methods in Geomechanics,1993,17(6)：357-383

22 刘干斌,谢康和,施祖元.黏弹性饱和多孔介质中圆柱孔洞的频域响应.力学学报,2004,36(5)：557-563(Liu Ganbin,Xie Kanghe, Shi Zuyuan.Frequency response of a cylindrical cavity in poroviscoelastic saturated medium.Acta Mechanica Sinica,2004,36(5)：557-563(in Chinese))

23 黄晓吉,扶名福,徐斌.移动环形载荷作用下饱和土中圆形衬砌隧洞动力响应研究.岩土力学,2012,33(3)：892-898(Huang Xiaoji, Fu Mingfu,Xu Bin.Dynamic response of a circular lining tunnel in saturated soil due to moving ring load.Rock and Soil Mechanics, 2012,33(3)：892-898(in Chinese))

24 Hasheminejad SM,Komeili M.Ef f ect of imperfect bonding on axisymmetric elastodynamic response of a lined circular tunnel in poroelastic soil due to a moving ring load.International Journal of Solids and Structures,2009,46：398-411

25 曾晨,孙宏磊,蔡袁强等.简谐载荷作用下饱和土体中圆形衬砌隧道三维动力响应分析.岩土力学,2014,35(4)：1147-1156(Zeng Chen，Sun Honglei，Cai Yuanqiang，et al.Analysis of threedimensionaldynamicresponseofacircularliningtunnelinsaturated soil to harmonic loading.Rock and Soil Mechanics,2014,35(4)：1147-1156(in Chinese))

26 曾晨,孙宏磊,蔡袁强等.饱和土体中衬砌隧道在移动载荷下的动力响应.浙江大学学报(工学版),2015,49(3)：511-521(Zeng Chen,Sun Honglei,Cai Yuanqiang,et al.Dynamic response of lined tunnel in saturated soil due to moving load.Journal of Zhejiang University(Engineering Science),2015,49(3)：511-521(in Chinese))

27 狄宏规,周顺华,陕耀等.基于改进壳-柱模型的盾构隧道饱和地基动应力解.同济大学学报（自然科学版），2016,44(9)：1384-1390(Di Honggui,Zhou Shunhua,Shan Yao,et al.Solution for dynamic stress of saturated soil surrounding a shield tunnel based on modifie shell-cylinder model.Journal of Tongji University(Natural Science),2016,44(9)：1384-1390(in Chinese))

28 邹炎.地下结构地震反应规律和抗震设计方法研究.[博士论文].北京：中国地震局工程力学研究所,2015(Zou Yan.Study on seismic response laws and seismic design methods of underground structures.[PhD Thesis].Beijing：Institute of Engineering Mechanics,China Earthquake Administration,2015(in Chinese))

29 高广运,何俊峰,李佳.地铁运行引起的饱和土地基动力响应.浙江大学学报(工学版),2010,44(10)：1925-1930(Gao Guangyun, He Junfeng,Li Jia.Dynamic response induced by running subway in saturated ground.Journal of Zhejiang University(Engineering Science),2010,44(10)：1925-1930(in Chinese))

30 袁宗浩,蔡袁强,曾晨.地铁列车载荷作用下轨道系统及饱和土体动力响应分析.岩石力学与工程学报,2015,34(7)：1470-1479 (Yuan Zonghao，Cai Yuanqiang，Zeng Chen.Dynamic response analysis of track system and underground railway tunnel in saturated soil subjected to a moving train load.Chinese Journal of Rock Mechanics and Engineering,2015,34(7)：1470-1479(in Chinese))

31 Biot MA.Theory of propagation of elastic waves in a fluid-saturate porous solid,I,low-frequency range.Journal Acoustic Social America,1956,28：168-178

32 Biot MA.Generalized theory of acoustic propagation in porous dissipative media.Journal Acoustic Social America,1962,34(9A)：1254-1264

33 Zimmerman C,Stern M.Boundary element solution of 3-D wave scatter problems in a poroelastic medium.Engineering Analysis with Boundary Elements,1993,12(4)：223-240

34 Lu JF,Jeng DS,Williams S.A 2.5-D dynamic model for a saturated porous medium：Part I.Green’s function.International Journal of Solids and Structures,2008,45(2)：378-391

35 Zhou SH,He C,Di HG.Dynamic 2.5-D Green’s function for a poroelastic half-space.Engineering Analysis with Boundary Elements,2016,67：96-107

36 Hasheminejad SM,Hosseini H.Nonaxisymmetric interaction of a spherical radiator in a fluid-fillpermeable borehole.International Journal of Solids and Structures,2008,45(1)：24-47

A 2.5-D COUPLED FE-BE MODEL FOR THE DYNAMIC INTERACTION BETWEEN TUNNEL AND SATURATED SOIL1)

He Chao2)Zhou Shunhua Di Honggui Xiao Junhua
(Key Laboratory of Road and Traf fic Engineering of the Ministry of Education,Tongji University,Shanghai201804,China)

This paper presents a 2.5-D coupled FE-BE model to simulate the three-dimensional dynamic interaction between saturated soils and tunnels with arbitrary sections.The tunnel is modeled using 2.5-D FEM and the ground is modeled using 2.5-D BEM for saturated porous media.The auxiliary problems are introduced to eliminate the Cauchy singularity of the 2.5-D boundary integral equation.The coupled FE-BE equations are obtained using the continuity conditions on the soil-tunnel interface.The presented model is appropriate for tunnels with arbitrary sections and high computational efficiency.The model is verifie through the comparison with the existing models.Finally,a case study of dynamic responses of a quasi-rectangular tunnel in saturated soil due to moving loads is presented.The ef f ects of soil permeability on displacements and pore pressure are investigated.The results show that：(1)The pore pressure decreases drastically with the increment of soil permeability,while displacements are not susceptible to soil permeability;(2)thepore pressure and displacements are mainly distributed in the vicinity of 2m around the loading point;(3)In the direction of gravity,the dissipation of the pore pressure beneath the tunnel is faster than that of displacements;the distributions along the depth to tunnel invert of pore pressure and axial displacement are evidently influence by the soil permeability.

saturated soil,special-section tunnel,dynamic response,coupled FE-BE,Fourier transformation

TU45

A doi：10.6052/0459-1879-16-176

2016-06-22收稿，2016-08-17录用,2016-08-24网络版发表.

1)国家自然科学基金资助项目(51478353).

2)何超，博士生，主要研究方向：轨道交通线路系统动力学.E-mail：1310756@tongji.edu.cn

何超，周顺华，狄宏规，肖军华.饱和土-隧道动力响应的2.5维有限元-边界元耦合模型.力学学报,2017,49(1)：126-136

He Chao,Zhou Shunhua,Di Honggui,Xiao Junhua.A 2.5D coupled FE-BE model for the dynamic interaction between tunnel and saturated soil.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1)：126-136